Волкова Е.С. Сборник домашних контрольных работ
Подождите немного. Документ загружается.

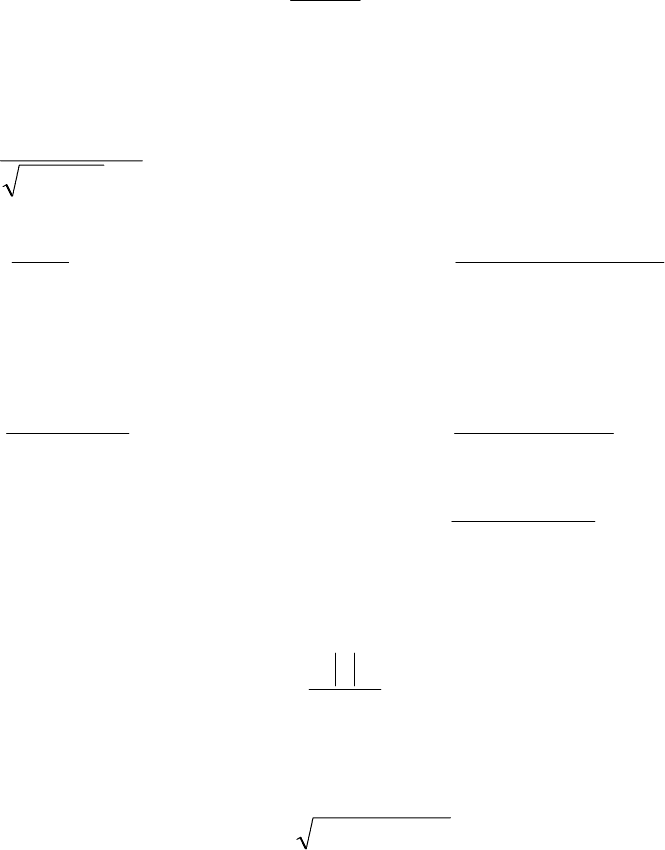
10
ВАРИАНТ 4
1. Пользуясь определением предела последовательности, докажите, что
1
5
25
lim =
−
∞→
n
n
n
.
2. Найти предел числовой последовательности:
а)
145
83
lim
2
++
+
∞→
n
n
n
; б)
(
)
345
328lim nnn
n
+−
∞→
;
в)
102
3
lim
−
∞→
+
n
n
n
n
; г)
(
)
(
)
()
6
5
12
cos31
lim
−
+−
∞→
n
nnn
n
.
3. Найти предел функции:
а)
4
2
1
32
lim
43
x
xx
xx
→−
++
++
; б)
2
1
1cos(3 3)
lim
21
x
x
xx
→
−
−
−+
;
в)
(
)
lim( 21) ln( 18) ln( 3)
x
xx x
→∞
−+−+; г)
()
x
xx
x
+
−
→
1ln
sin3sin
lim
0
.
4. Найти и исследовать точки разрыва функции
xx
x
y
+
=
2
.
5. Найти асимптоты графика функции, если:
1242
2
++−= xxxy .
6
*
. Доказать, что уравнение
01881713
23
=
−
+
+
x
x
x
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
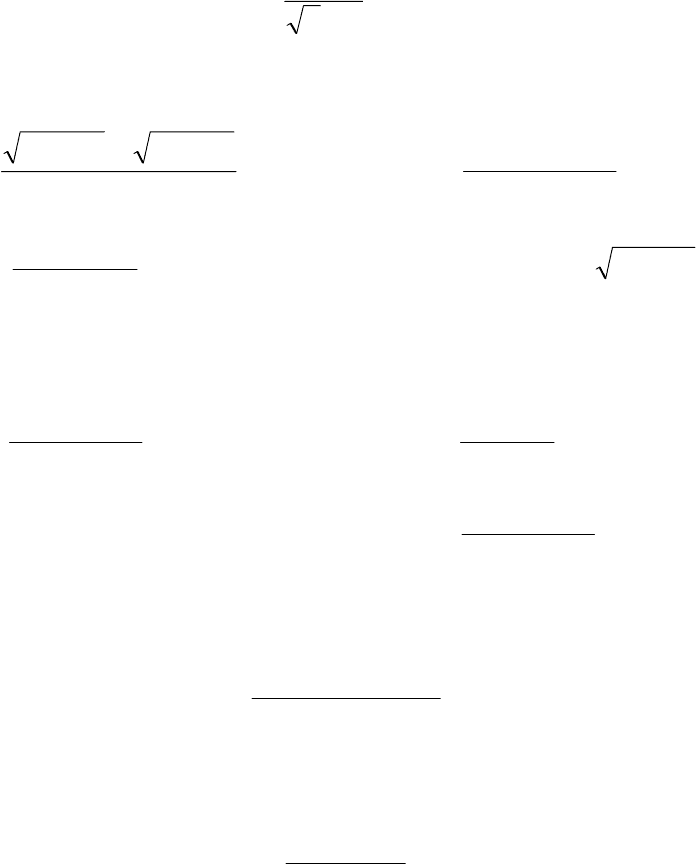
11
ВАРИАНТ 5
1. Пользуясь определением предела последовательности, докажите, что
0
5
1
lim =
+
∞→
n
n
.
2. Найти предел числовой последовательности:
а)
3
3232
lim
22
−−+
∞→
nn
n
; б)
nnn
nn
n
−+
+−
∞→
34
43
36
257
lim
;
в)
n
n
nn
nn
2
2
2
33
12
lim
−+
−+
∞→
; г)
(
)
(
)
(
)
nnn
n
−++
∞→
1612coslim
2
.
3. Найти предел функции:
а)
3
2
3
512
lim
43
x
xx
xx
→−
−+
++
; б)
24
2
0
8
lim
sin 3
x
x
x
x
→
+
;
в)
(
)
42
lim 5 2 3
x
x
xx
→∞
−+ −; г)
36
2
1
lim
arctg( 2)
x
x
e
x
+
→−
−
+
.
4. Найти и исследовать точки разрыва функции
2
| 5 | sin( 1)
65
xx
y
xx
+
⋅+
=
++
.
5. Найти асимптоты графика функции, если:
3
2
10
4
xx
y
x
+
−
=
−
.
6
*
. Доказать, что уравнение
54
971340
x
xx
−
+−=
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
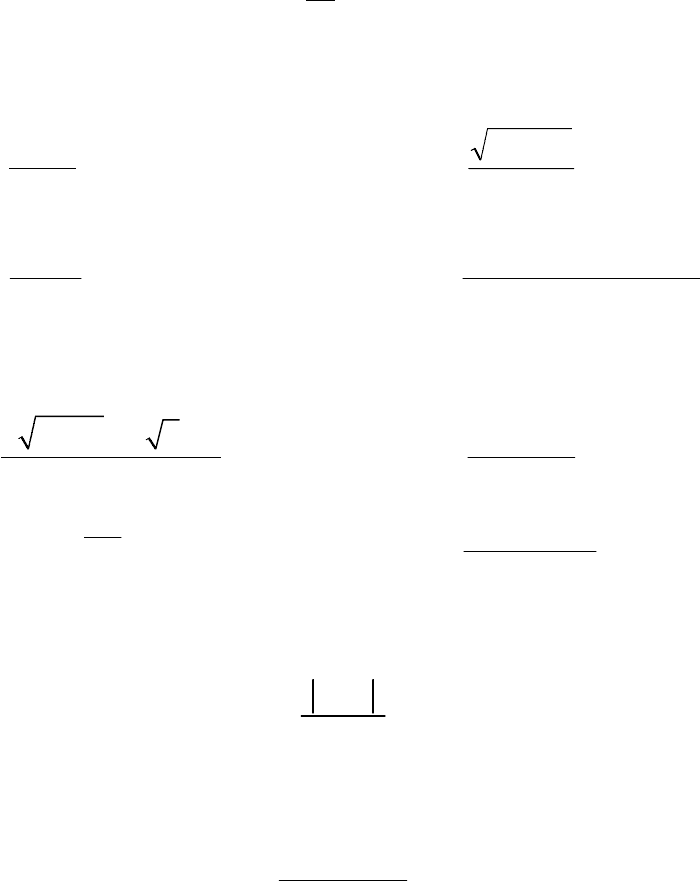
12
ВАРИАНТ 6
1. Пользуясь определением предела последовательности, докажите, что
0
3
1
lim =
∞→
n
n
.
2. Найти предел числовой последовательности:
а)
−
+
+
∞→
n
n
n
n
2
1
lim
2
; б)
162
84
lim
2
+
+
∞→
n
n
n
;
в)
n
n
n
n
71
72
37
lim
+
∞→
+
−
; г)
(
)
()
()
7
4
3
3
4sin52
lim
n
nnn
n
+
−−
∞→
.
3. Найти предел функции:
а)
4
2
2273
lim
6
x
xx
xx
→∞
+− +
−−
; б)
x
xx
x
4cos1
3sin
lim
0
−
→
;
в)
()
25
1
1
lim 2 1
x
x
x
x
+
−
→
− ; г)
(
)
2
2
0
4sin
71ln
lim
x
x
x
+
→
.
4. Найти и исследовать точки разрыва функции
2
2
2
x
y
x
x
+
=
+
.
5. Найти асимптоты графика функции, если:
5
44
2
+
−+
=
x
xx
y .
6
*
. Доказать, что уравнение
045193511
23
=
−
+
+
x
x
x
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
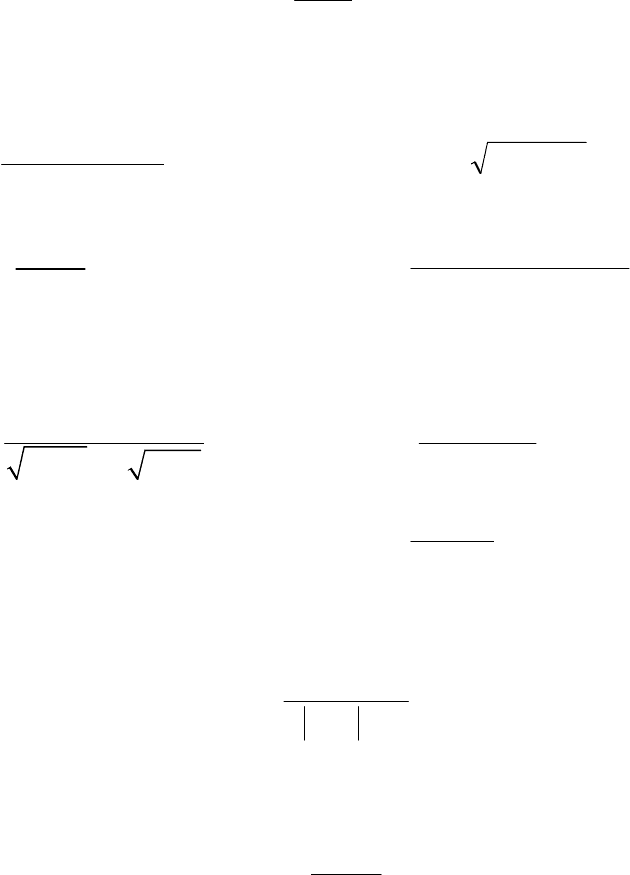
13
ВАРИАНТ 7
1. Пользуясь определением предела последовательности, докажите, что
2
5
2
lim =
+
∞→
n
n
n
.
2. Найти предел числовой последовательности:
а)
2
316
lim
24 2
n
nn
n
→∞
+
++ +
K
; б)
(
)
nnn
n
842lim
2
−−
∞→
;
в)
2
21
2
2
4
lim
nn
n
n
n
−−
→∞
+
; г)
(
)
(
)
()
2
2
3
22
853sin
lim
−
+−
∞→
n
nnn
n
.
3. Найти предел функции:
а)
2
4
32
lim
15 6
x
xx
xx
→∞
++
+− +
; б)
(
)
1
ln 6 5
lim
8( 1)
x
x
x
→−
+
+
;
в)
(
)
lim 3 ln( 5) ln( 3)
x
xx x
→∞
⋅−−−; г)
xx
xx
x
57
78
lim
0
−
−
→
.
4. Найти и исследовать точки разрыва функции
(1)sin
1
x
x
y
x
x
−
=
−
⋅
.
5. Найти асимптоты графика функции, если:
2
3
2
x
x
y
−
= .
6
*
. Доказать, что уравнение
54
53120
x
xx
−
+−=
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
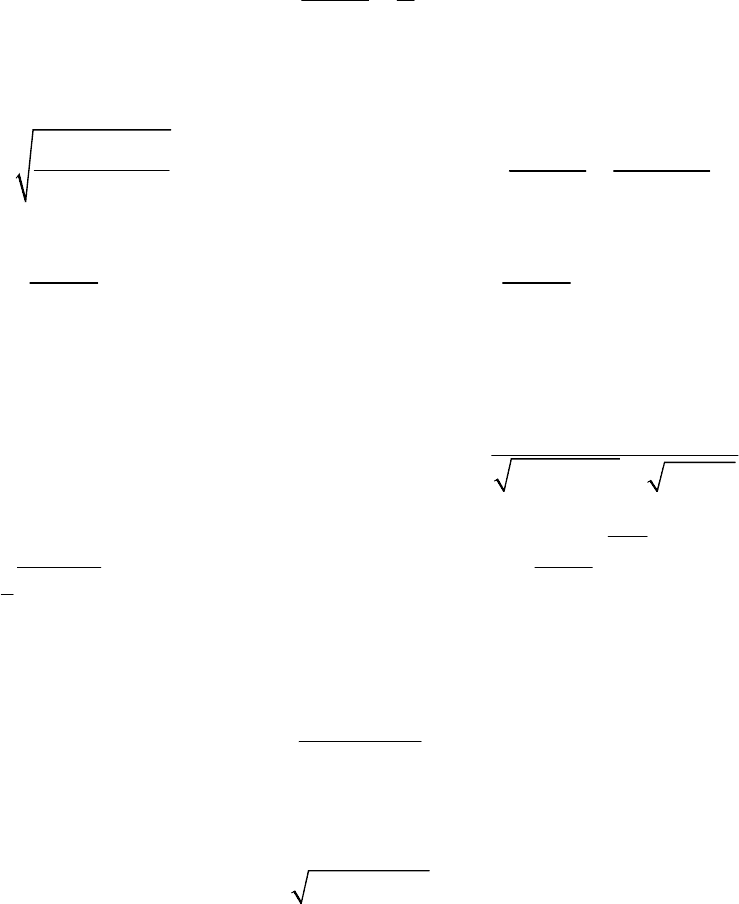
14
ВАРИАНТ 8
1. Пользуясь определением предела последовательности, докажите, что
515
lim
12 2
n
n
n
→∞
+
=
+
.
2. Найти предел числовой последовательности:
а)
2
2
233
lim
11 4
n
nn
nn
→∞
+−
−+
; б)
22
3123
lim
21
n
nnn
nn
→∞
+−
+
+−
;
в)
2
25
2
2
5
lim
3
nn
n
n
n
−+
→∞
+
−
; г)
2
2
1
lim cos(2 1)
5
n
n
n
→∞
⋅−
+
.
3. Найти предел функции:
а)
(
)
43
lim 3 10
x
xx
→∞
−+−
; б)
2
2
1
2
lim
422
x
xx
xx x
→
+−
−
+− +
;
в)
4
sin(4 )
lim
4
x
x
x
π
π
→
−
; г)
1
sin 3
0
lim 1
cos
x
x
x
x
→
−
.
4. Найти и исследовать точки разрыва функции
2
sin( 2)
32
x
y
xx
−
=
−
+
.
5. Найти асимптоты графика функции
2
23yx x
=
−+.
6
*
. Доказать, что уравнение
3
10 1 0
x
x
−
+=
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
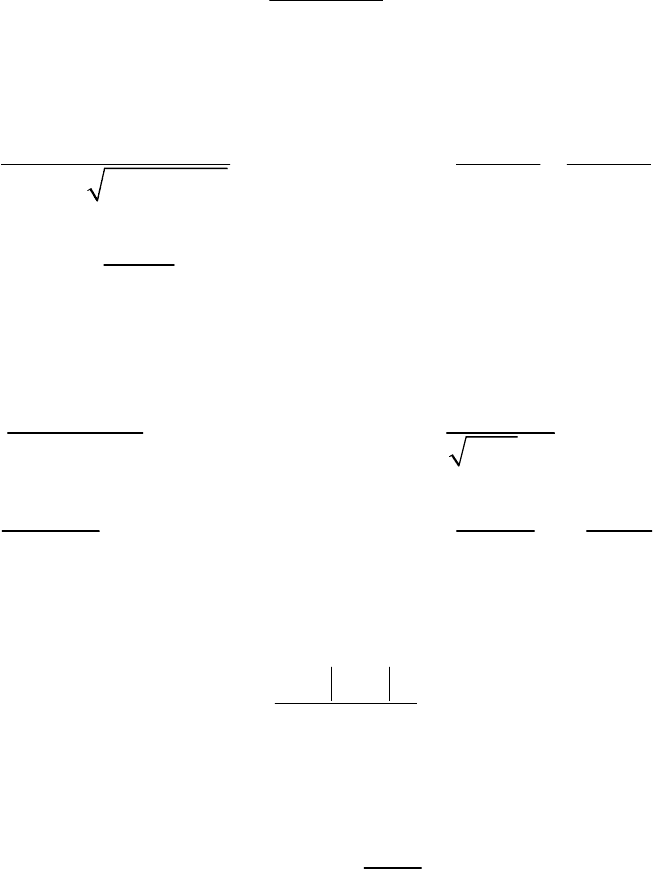
15
ВАРИАНТ 9
1. Пользуясь определением предела последовательности, докажите, что
2(1)
lim 1
2
nn
n
n→∞
+−
=
.
2. Найти предел числовой последовательности:
а)
4
32
(3 1)
lim
(5) 72
n
n
nnn
→∞
−
+−+
; б)
22
442
lim
25 3
n
nn n
nn
→∞
−+
−
++
;
в)
1
lim arctg
32
n
n
n
→∞
⋅
+
; г)
(
)
lim(3 1) ln(2 ) ln(2 7)
n
nnn
→∞
−
⋅−+
.
3. Найти предел функции:
а)
2
4
1
253
lim
325
x
xx
xx
→−
++
−−
; б)
0
lim
11
x
x
x
→
+
−
;
в)
0
sin 2
lim
1cos
x
x
x
x
→
⋅
−
; г)
2
21 3
lim sin
231
x
x
xx
→∞
−
⋅
+
+
.
4. Найти и исследовать точки разрыва функции
2
3
(43)
xx
y
xx
⋅+
=
+
+
.
5. Найти асимптоты графика функции
cos
25
3
x
yx
x
=−− .
6
*
. Доказать, что уравнение
06161911
23
=
−
+
+
x
x
x
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
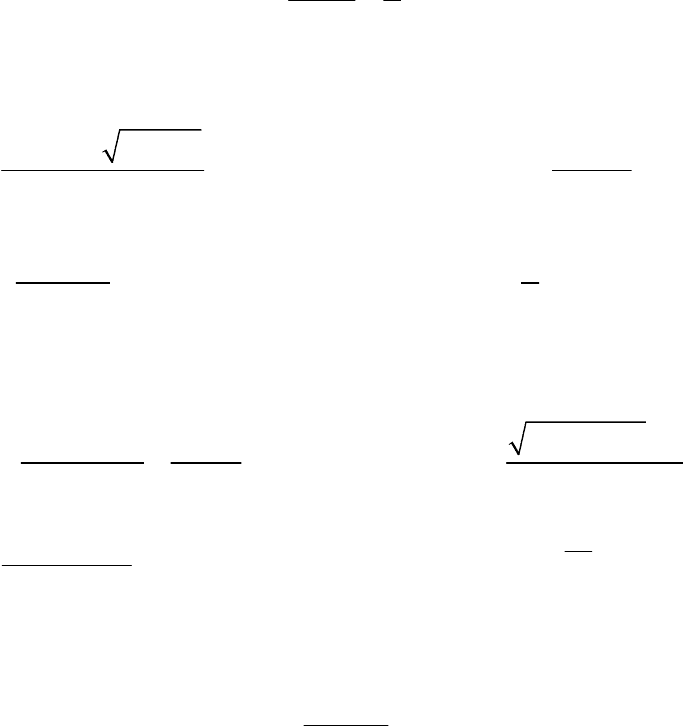
16
ВАРИАНТ 10
1. Пользуясь определением предела последовательности, докажите, что
212
lim
99
n
n
n
→∞
−
=
.
2. Найти предел числовой последовательности:
а)
22
3
(2 3) 2 9
lim
(6)
n
nn
n
→∞
++
−
; б)
3
2
35
lim 3
1
n
n
n
n
→∞
−
−
+
;
в)
32
43
lim
43 3
n
n
n
n
+
→∞
⋅
⋅−
;
г)
2
1
lim tg cos( )
n
n
n
→∞
⋅
.
3. Найти предел функции:
а)
2
1
35 23
lim
43 1
x
xx
xx x
→−
++
−
++ +
; б)
2
1
331
lim
1
x
xx
x
→−
+
+−
+
;
в)
0
1cos
lim
3arcsin
x
x
x
x
→
−
⋅
; г)
()
4
3
3
lim 2
x
x
x
−
→
− .
4. Найти и исследовать точки разрыва функции
2
sin 2
2
x
y
x
x
=
+
.
5. Найти асимптоты графика функции
2
(1)
x
yx e
=
+⋅ .
6
*
. Доказать, что уравнение
528
34
=
+
x
x
имеет хотя бы один положительный действительный корень, и найти его
приближенное значение с точностью до сотых (решение обосновать).
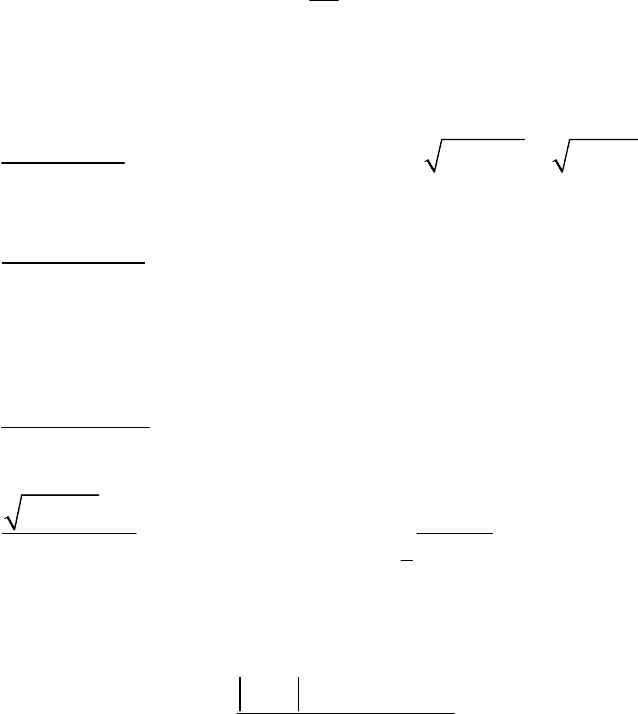
17
ВАРИАНТ 11
1. Пользуясь определением предела последовательности, докажите, что
1
lim 0
2
n
n→∞
=
.
2. Найти предел числовой последовательности:
а)
3
2
(7 8)
lim
25
n
n
nn
→∞
+
++
; б)
(
)
22
lim 2
n
nnnn
→∞
+
−−;
в)
2
12
lim
25
n
n
n
→∞
++ +
+
K
; г)
(
)
lim( 6) ln(3 5) ln(3 2)
n
nnn
→∞
−
⋅+−+.
3. Найти предел функции:
а)
2
43
2
514
lim
740
x
xx
xx
→
+−
−+
; б)
(
)
sin
0
lim 1 cos(1/ )
x
x
ex
→
−⋅ ;
в)
0
1tg 1
lim
x
x
x
→
+−
; г)
2
2
lim
cos
x
x
x
π
π
→
−
.
4. Найти и исследовать точки разрыва функции
2
2
5( 3 4)
45
xxx
y
xx
−
⋅−−
=
−−
.
5. Найти асимптоты графика функции
6arctg( 3)yx x=+− − .
6
*
. Доказать, что уравнение
010283319
23
=
−
+
+
x
x
x
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
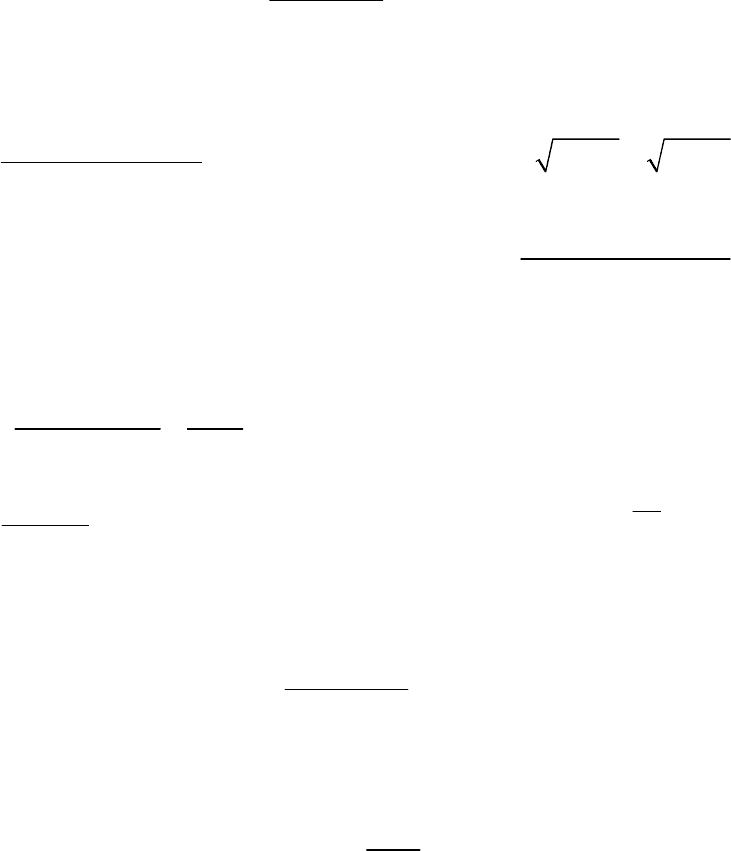
18
ВАРИАНТ 12
1. Пользуясь определением предела последовательности, докажите, что
(1) 4
lim 1
4
nn
n
n→∞
−+
=
.
2. Найти предел числовой последовательности:
а)
6
24
(4 1)
lim
(5 2) (2 3)
n
n
nn
→∞
−
++
; б)
(
)
22
lim 3 5
n
nn
→∞
+− − ;
в)
(
)
lim(2 ) ln( 4) ln( 3)
n
nn n
→∞
⋅−−+
; г)
2
21
lim
13 (2 1)
n
n
n
→∞
+
+
++ +K
.
3. Найти предел функции:
а)
32
2
3
61716
lim
23 3
x
xx
xx x
→
+−
−
−− −
; б)
(
)
2
0
lim (tg ) sin(1/ )
x
x
xx
→
+⋅ ;
в)
3
3
lim
sin( )
x
x
x
π
→
−
; г)
()
7
2
0
lim 1 tg(3 )
x
x
x
−
→
+ .
4. Найти и исследовать точки разрыва функции
2
sin( 1)
54
x
y
xx
+
=
+
+
.
5. Найти асимптоты графика функции
sin
32
1
x
yx
x
=++
−
.
6
*
. Доказать, что уравнение
32
21530
x
x
+
−=
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
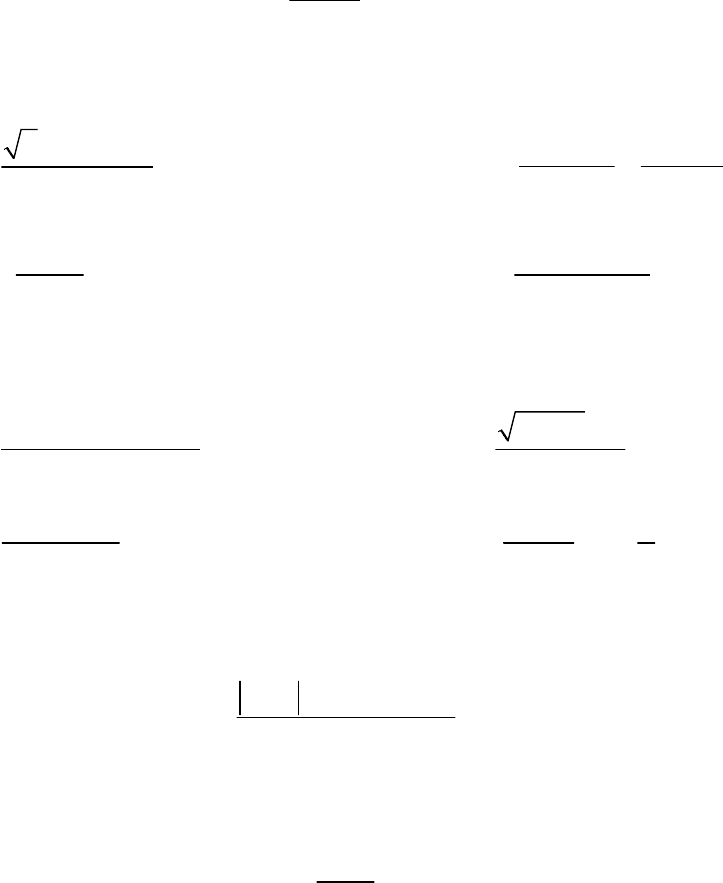
19
ВАРИАНТ 13
1. Пользуясь определением предела последовательности, докажите, что
65
lim 3
2
n
n
n
→∞
−
=
.
2. Найти предел числовой последовательности:
а)
2
4
(5 9)
lim
(3)
n
nn
n
→∞
⋅+
−
; б)
32 3
23
lim
24 2
n
nn nn
nn
→∞
++
−
+
;
в)
3
2
1
lim sin( 5)
3
n
n
n
n
→∞
+
⋅+
+
; г)
2
2
2
235
lim
27
n
n
nn
nn
−
→∞
+−
++
.
3. Найти предел функции:
а)
43
2
3
2512
lim
9
x
xxx
x
→
−−−
−
; б)
3
233
lim
3
x
x
x
→
+
−
−
;
в)
2
0
sin 2
lim
ln(1 3 )
x
x
x
x
→
⋅
+
; г)
3
2
2
lim sin
23
x
x
x
x
→∞
⋅
+
.
4. Найти и исследовать точки разрыва функции
2
2
3( 3 2)
56
xxx
y
xx
+
⋅++
=
++
.
5. Найти асимптоты графика функции
2
x
e
y
x
=
−
.
6
*
. Доказать, что уравнение
090766913
23
=
−
+
+
x
x
x
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
