Voit J. The Statistical Mechanics of Financial Markets

Подождите немного. Документ загружается.

160 5. Scaling in Financial Data and in Physics

(t) describes a Wiener process. With v(t)=σ

(t), the time-dependent

variance again follows a stochastic process

dv(t)=m(v)dt + s(v)dz

. (5.113)

Several popular models use diﬀerent speciﬁcations for m(v)ands(v) [10]:

m(v)=γv , s(v)=κv (Rendleman −Bartter model),

m(v)=γ(θ − v) ,s(v)=κ (Vasicek model),

m(v)=γ(θ − v) ,s(v)=κ

√

v (Cox − Ingersoll − Ross model).

(5.114)

In the Vasicek and Cox–Ingersoll–Ross models, the volatility is mean-reverting

with a time constant γ

−1

and an equilibrium volatility of θ.

The leverage eﬀect suggests that the volatility and return processes may

be correlated in addition:

(t)=ρ

r−v

(t)+

1 − ρ

r−v

dZ(t) , (5.115)

where dZ(t) describes a Wiener process independent of dz

(t). Recently, the

Cox–Ingersoll–Ross model with a ﬁnite return-volatility correlation ρ

r−v

has

been solved for its probability distributions [119], extensively using Fokker–

Planck equations. The logarithmic probability distributions for log-returns on

short time scales (1 day) are almost triangular in shape, while they become

more parabolic for longer time scales, e.g., 1 year.

For long time scales γτ  1, the probability distribution of x

(t)=

δS

(t) −δS

(t) takes the scaling form

P (x

)=N

−p



(z) ,P



(z)=K

(z)/z . (5.116)

is a time-scale-dependent normalization constant, p

is a constant depend-

ing on the return-volatility correlations and the parameters of the volatility

process, and K

(z) is the modiﬁed Bessel function. The argument z is of

the schematic form z

=(ax

+ b)

+ c

[119]. In the limit of large returns,

ln P (x

) ∼−p

− (...)|x

|, i.e., the tails of the probability distribution of

the returns are exponential with a diﬀerent slope for the positive and nega-

tive returns. These slopes, however, do not depend on the time scale τ in this

long-time-scale limit. The exponential tails are reminiscent of some variants

of the truncated L´evy distributions discussed in Sect. 5.3.3. In the limit of

small returns at long time scales, a skewed Gaussian distribution of returns

is obtained. When the solutions are compared to 20 years of Dow Jones data,

an excellent collapse onto a single master curve is obtained for time scales

from 10 days to 1 year with four ﬁtting parameters only, γ, θ, κ, µ. Indepen-

dently, the correlation coeﬃcient ρ

r−v

has been found to vanish [119]. These

four parameters are summarized in Table 5.3, where they are given both in

daily and annual units.

5.6 Non-Stable Scaling and Correlations in Financial Data 161

Table 5.3. Parameters of the stochastic volatility model obtained from the ﬁt of

the Dow Jones data. In addition to the parameters listed, ρ = 0 for the correlation

coeﬃcient and 1/γ =22.2 trading days for the relaxation time of the variance are

found

Units γθκµ

1/day 4.50 × 10

−2

8.62 × 10

−5

2.45 × 10

−3

5.67 × 10

−4

1/year 11.35 0.022 0.618 0.143

5.6.5 Cross-Correlations in Stock Markets

With the exception of the Black–Scholes analysis where we used the correla-

tions in price movements between an option and its underlying security, we

have not yet considered possible correlations between ﬁnancial assets. How-

ever, it would be implausible to assume that the price movements of a set of

stocks in a market are completely uncorrelated. There are periods where a

large majority of stocks moves in one direction, and thus the entire market

goes up or down. On the other hand, in other periods, the market as a whole

moves quite little, but sectors might move against each other, or within an

industry share values of diﬀerent ﬁrms could move against each other, either

as a result of changing market share, or due to more psychological factors.

Can correlations between diﬀerent stocks be quantiﬁed, or those between

stocks and the market index be quantiﬁed? As will become apparent in

Chap. 10, knowing such correlations accurately is a prerequisite for good

risk management in a portfolio of assets. Unfortunately, it turns out that

many of these correlations are hard to measure.

Correlations between the prices or returns of two assets γ and δ are mea-

sured by the correlation matrix

C(γ,δ)=





δS

(γ)

(t) −δS

(γ)

(t)



δS

(δ)

(t) −δS

(δ)

(t)





(γ)

(δ)

(5.117)

≡



t=1

δs

(γ)

(t)δs

(δ)

(t) . (5.118)

A time scale τ = 1 day has been assumed for the returns, and the corre-

sponding subscript has been dropped, δS

(γ)

(t) ≡ δS

(γ)

(t). We also assume

stationary markets, i.e. C(γ,δ) is time-independent. The returns δS

(γ)

(t)

have been deﬁned in (5.1), σ

(γ)

are their standard deviations, the normalized

returns δs

(γ)

were deﬁned in (5.2), and the averages ... are taken over time.

Uncorrelated assets have C(γ,δ)=δ

γ,δ

. In ﬁnance, the label β is reserved for

the correlation of a stock γ (or a portfolio of stocks) with the market [10]:

β = C(γ, market) . (5.119)

162 5. Scaling in Financial Data and in Physics

In order to appreciate the subsequent discussion, let us look at two un-

correlated time series δs

(1)

(t)andδs

(2)

(t), each of length T (and zero mean,

unit variance, of course). From (5.117), we have

C(1, 2) =



t=1

δs

(1)

(t)δs

(2)

(t) . (5.120)

C(1, 2) is the sum of T random variables with zero mean. Despite the ab-

sence of correlations (by construction) between the two time series, for ﬁnite

T , C(1, 2) is a random variable itself and diﬀerent from zero. C(1, 2) is drawn

from a distribution with zero mean and a standard deviation decreasing as

√

T . Only in the limit T →∞will C(1, 2) → 0, as is appropriate for uncor-

related random variables. The ﬁnite time scale T , over which the correlations

between the two time series are determined, produces a noise dressing of the

correlation coeﬃcient. More speciﬁcally, for two independent time series of

length T of normally distributed random numbers ε

(t) with zero mean and

unit variance, the correlation coeﬃcient again is a random number [120]

ε

(t)ε

(t) = δ



1+δ

(t) . (5.121)

The ﬁnite-length autocorrelation is a random normally distributed variable

with mean unity and variance 2/T , and the cross-correlation is a random

normally distributed variable with zero mean and variance 1/T.

For correlation matrices where many time series enter, noise dressing may

be a severe eﬀect. N time series with T entries each may be grouped into an

N ×T random matrix M, and the correlation matrix is written as C = T

−1

M · M where M is the transpose of M. In the same way as noise dressing

for ﬁnite T produced an artiﬁcial ﬁnite random value for C(1, 2), for ﬁnite T ,

noise dressing will produce artiﬁcial ﬁnite random entries C(γ, δ) in the corre-

lation matrix. Figure 5.26 demonstrates this eﬀect: the correlation matrix C

of 40 uncorrelated time series is random when the time series is only 10 steps

long (left panel). The absence of correlations C(γ,δ)=δ

γ,δ

is well visible for

1000 time steps (right panel). The two panels of Fig. 5.26 are consistent with

(5.121). For T = 10, the autocorrelation is a Gaussian variable with mean

unity and standard deviation 0.48, and the cross-correlation coeﬃcients are

Gaussians with mean zero and standard deviations of 0.32. For T = 1000,

the mean values are the same but standard deviations have decreased by

one order of magnitude. Roughly, for N time series, T  N time steps are

required in the series in order to produce statistically signiﬁcant correlation

matrices.

Random matrix theory predicts the spectrum of eigenvalues λ of a ran-

dom matrix (of the type appropriate for ﬁnancial markets [121, 122]) to be

bounded and distributed according to a density

ρ(λ)=

2πσ



(λ

max

− λ)(λ − λ

min)

5.6 Non-Stable Scaling and Correlations in Financial Data 163

-0.5

0.5

0.25

0.5

0.75

Fig. 5.26. Noise dressing of a correlation matrix. The correlation matrix of 40

uncorrelated time series is shown for a length of 10 steps (left panel) and 1000 steps

(right panel)

max

min

= σ



± 2





, (5.122)

where Q = T/N ≥ 1 is the ratio of time series entries to assets. This density

is shown as the dotted line in Fig. 5.27.

Recently, two groups calculated the correlation matrices of large samples

of stocks from the US stock markets [121, 122], and compared their results

to predictions from random matrix theory. This is partly done with refer-

ence to the complexity of a real market (a detailed analysis of all correlation

coeﬃcients would not be useful) and partly in order to compare empirical

correlations with a null hypothesis (purely random correlations, the alterna-

tive null hypothesis of zero correlations being rather implausible). Random

matrix theory was developed in nuclear physics in order to deal with the en-

ergy spectra of highly excited nuclei in a statistical way when the complexity

of the spectra made the task of a detailed microscopic description hopeless

[123] – a situation reminiscent of ﬁnancial markets.

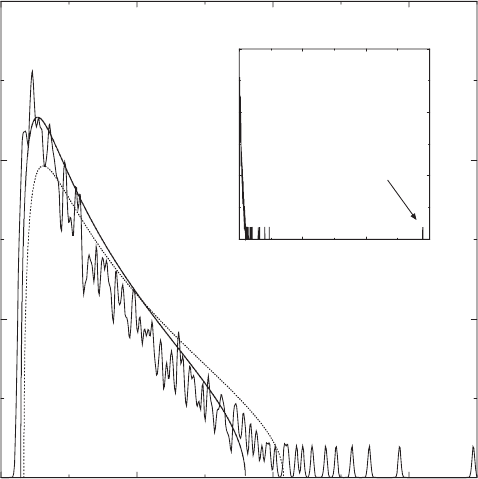
Figure 5.27 displays the eigenvalue density of the correlation matrix of 406

ﬁrms out of the S&P500 index based on daily closes from 1991 to 1996 [121].

Similar results are available also for other samples of the US stock market

[122]. A very large part of the eigenvalue spectrum is indeed contained in the

density predicted by random matrix theory, and therefore noise-dressed.

There are some eigenvalues falling outside the limits of (5.122), however,

which contain more structured information [121, 122]. The most striking is

the highest eigenvalue λ

≈ 60. Its eigenvector components are distributed

approximately uniformly over the companies, demonstrating that this eigen-

value represents the market itself. Another 6% of the eigenvalues fall outside

the random matrix theory prediction for the spectral density but lie close to

its upper end. An evaluation of the inverse participation ratio of the eigen-

vectors [122] suggests that there may be a group of about 50 ﬁrms with def-

initely non-random correlations which are responsible for these eigenvalues.

164 5. Scaling in Financial Data and in Physics

0 204060

ρ(λ)

0123

ρ(λ)

Market

Fig. 5.27. Density of eigenvalues of the correlation matrix of 406 ﬁrms out of the

S&P500 index. Daily closing prices from 1991 to 1996 were used. The dotted line is

the prediction of random matrix theory. The solid line is a best ﬁt with a variance

smaller than the total sample variance. The inset shows the complete spectrum

including the largest eigenvalue which lies about 25 times higher than the body

of the spectrum. By courtesy of J.-P. Bouchaud. Reprinted from L. Laloux et al.:

Phys. Rev. Lett. 83, 1467 (1999),

1999 by the American Physical Society

Interestingly, high inverse participation ratios are also found for some very

small eigenvalues. While they apparently fall inside the spectral range of ran-

dom matrix theory, the high values found here seem to give evidence for

possibly small groups of ﬁrms with strong correlations [122]. However, these

groups would not have signiﬁcant cross-group correlations.

Kwapi´en et al. have shown that drawing 451 time series of length 1948

each out of a Gaussian distribution produces a remarkably good approxima-

tion to (5.122) [124]. For ﬁxed N, Q increases with T ,andλ

max

and λ

min

approach each other and both approach σ

(σ = 1 in our case). We there-

fore recover an N-fold-degenerate eigenvalue 1, as expected for uncorrelated

variables.

The empirical properties of the S&P500 correlation matrices can be clari-

ﬁed further using a model of group correlations [125]. Here, one assumes that

industries cluster in groups (labeled by g while the individual ﬁrms are labeled

5.6 Non-Stable Scaling and Correlations in Financial Data 165

by γ), and that the return of a stock contains both a “group component” and

an “individual component”

δs

(γ)

(t)=



1+w

(t)+



1+w

(t) . (5.123)

(t)andε

(t) are both random numbers and represent the synchronous

variation of the returns within a group, and the individual component with

respect to the group, respectively. The relative weight of the group dynamics

with respect to the individual dynamics is measured by the weight factor

. In the model, there may also be a number of companies which do not

belong to a group. They formally obtain a weight factor w =0.Thisisa

straightforward generalization of the one-factor model (5.99) introduced when

discussing variety. There is no built-in correlation between industries. With

inﬁnitely long time series, the correlation matrix of the model without in-

group randomness [ε

(t) ≡ 0] is a block diagonal matrix. It is a direct product

of N

× N

matrices whose entries are all unity (N

is the size of group g).

These blocks have one eigenvalue equal to N

,andN

−1 eigenvalues equal to

zero. When the time series are ﬁnite, and the ﬁrms have an individual random

component in their returns, the eigenvalues will be changed. The inﬂuence

on the eigenvalue N

will be minor so long as the individual randomness is

not too strong. However, the most important eﬀect will be a splitting of the

− 1)-fold-degenerate zero eigenvalues into a ﬁnite spectral range. Under

special circumstances, one may also observe high inverse participation ratios

for small eigenvalues [125]. This happens when the noise strength of a group

is small, i.e., when the variance of the “individual ﬁrm contribution” to the

returns is small compared to the variance of the “group contribution”. This

eﬀect is also seen in numerical simulations [125].

A nice feature of this model is that its correlation coeﬃcients can be de-

termined analytically for ﬁnite times series lengths T [120] when the price

dynamics is governed by geometric Brownian motion (returns normally dis-

tributed). From (5.117) and using (5.121), we ﬁnd

C(γ,δ; T )=



1+w



1+w



1+δ



1+w



1+w

γδ



1+δ

γδ



1+w



1+w

√



1+w



1+w

√

γh

(5.124)

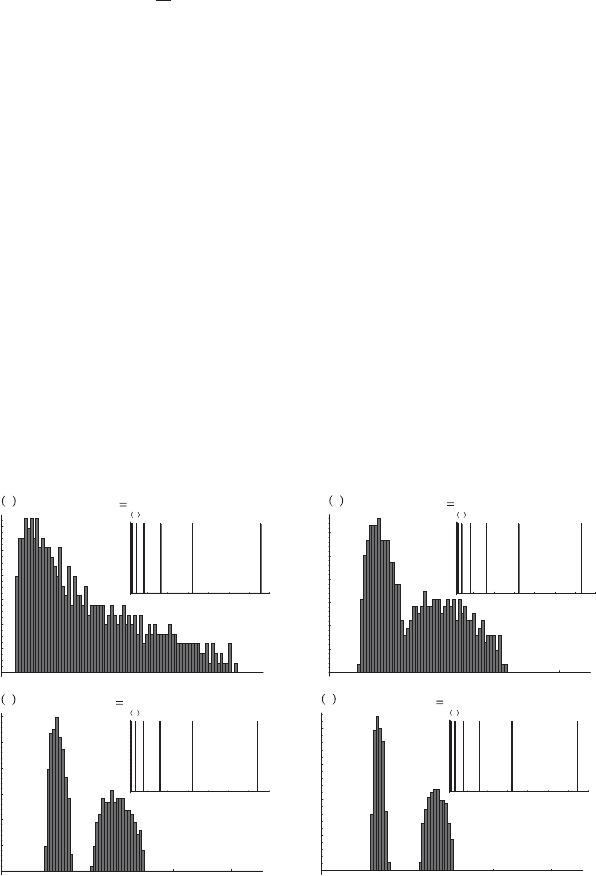
166 5. Scaling in Financial Data and in Physics

to leading order in

√

T . The indexation of the four random numbers ε is

meant to indicate that they are diﬀerent and independent, but is irrelevant

else.

Moreover, the model can be simulated numerically quite easily. When

comparable parameters are used, an eigenvalue spectrum similar to Fig. 5.27

is obtained. This is demonstrated in Fig. 5.28. In that simulation it was

assumed that assume that, among N = 508 stocks considered, there are six

correlated groups g =1,...,6 with sizes growing as 2

g+1

and weights w

1 − 2

−g−1

. The sizes increase from 4 to 128 companies, and weight factors

increase from 0.75 to 0.99 [120]. The remaining 256 stocks were supposed to

be uncorrelated.

For a time series length of T =1, 650, the spectrum in the top left panel

of Fig. 5.28 is rather similar to 5.27. When the length of the time series is

increased to T =5, 000 and on to T =50, 000, the structure of the eigenvalue

spectrum of the correlation matrix is changed. The bulk of the spectrum ﬁrst

develops a bimodal structure and subsequently splits into two distinct and

clearly separated spectra, one centered around λ =0.5 and the other spec-

trum centered around λ = 1. In addition, we still have the large eigenvalues

discussed in the analysis of the S&P500 data.

0.5

1.5

0.2

0.4

0.6

0.8

1.2

L 1650

10.

20.

30.

40.

50.

60.

70.

0.0005

0.001

0.0015

0.002

0.5

1.5

0.25

0.5

0.75

1.25

1.5

L 5000

10.

20.

30.

40.

50.

60.

70.

0.0005

0.001

0.0015

0.002

0.5

1.5

0.5

1.5

2.5

L 20000

10.

20.

30.

40.

50.

60.

70.

0.0005

0.001

0.0015

0.002

0.5

1.5

L 50000

10.

20.

30.

40.

50.

60.

70.

0.0005

0.001

0.0015

0.002

Fig. 5.28. Spectral densities ρ

(λ) of simulated correlation matrices. The

length of the time series increases from top left to bottom right as T =

1, 650, 5, 000, 20, 000, 50, 000. The densities are split into two regions, 0 ≤ λ ≤ 2.2

(main body of each panel) and 2.2 ≤ λ ≤ 70 (inset of each panel). The densities

are given in units of N.BycourtesyofB.K¨alber. Reprinted from T. Guhr and B.

K¨alber: J. Phys. A: Math. Gen. 36, 3009 (2003),

2003 by the Institute of Physics

5.6 Non-Stable Scaling and Correlations in Financial Data 167

Extending Noh’s argument [125], we can attribute the three groups of

spectra to diﬀerent mechanisms. The large eigenvalues outside the spectrum

described by random matrix theory, consist of the market component and

the large eigenvalues of each individual industry. The eigenvalues centered

around λ =0.5 represent intra-industry correlations. For every industry,

there is an almost N

−1-fold degenerate eigenvalue at λ =1/(1+w

)which,

with w

-factors in the range 0.75 ...0.99, lies close to λ =0.5. (The N

eigenvalue of the industry group is among the “large” eigenvalues.) These

eigenvalues descend from the N

−1-fold degenerate zero eigenvalue obtained

in the simpliﬁed problem where all entries of the intra-industry correlation

matrix equal unity. Finally, the group of eigenvalues around λ = 1 represents

the trivial autocorrelation of those companies which do not belong to any

industry group.

The detailed understanding of the T -scaling of the entries of the correla-

tion matrix, (5.124), in the Noh model [125] allows to formulate a heuristic

method called power mapping, to identify instrinsic correlations in a broad

eigenvalue spectrum such as that shown in Fig. 5.27. Power mapping is equiv-

alent to artiﬁcially extending the length T of the time series underlying the

correlation matrix [120]. Power mapping is achieved by raising every element

of the correlation matrix to its q

power

(q)

(γ,δ; T )=sign[C(γ,δ; T )] |C(γ, δ; T )|

. (5.125)

Notice that the power-mapped matrix C

(q)

(γ,δ; T ) is diﬀerent from the q

power of the correlation matrix [C(γ,δ; T )]

. Now consider the inﬂuence of

this mapping on the three diﬀerent types of contributions to C(γ,δ; T ). The

diagonal terms

C(γ,γ; T ) ∼ 1+

1/2

→ C

(q)

(γ,γ; T ) ∼ 1+q

1/2

, (5.126)

where b

is a constant. The intra-industry oﬀ-diagonal terms g = h but γ = δ

are mapped as

C(γ,δ; T ) ∼ a +

1/2

→ C

(q)

(γ,γ; T ) ∼ a

+ q

1/2

, (5.127)

with constants 0 <a<1andb

. The terms oﬀ-diagonal both in industry

and in company index, on the other hand, behave as

C(γ,δ; T ) ∼

1/2

→ C

(q)

(γ,γ; T ) ∼



1/2



∼ T

−q/2

. (5.128)

When q>1, the decay of these terms is accelerated by power-mapping with

respect to the diagonal or intra-industry oﬀ-diagonal terms. It is for this

suppression of oﬀ-diagonal noise-induced correlation coeﬃcients that power-

mapping is equivalent to a prolongation of the time series.

168 5. Scaling in Financial Data and in Physics

Numerical simulations of the Noh model conﬁrm that power mapping with

q>1 acts to reduce the noise dressing of the correlation matrix. With q =1.5,

a clear two-peak structure in the eigenvalue spectrum is visible when the

original (q = 1) spectrum looked similar to Fig. 5.27. All three components of

the eigenvalue spectrum, intra-industry correlations, isolated companies, and

industry and market collective contributions are readily apparent. However, it

turns out that the range of powers q where the mapping separates the spectral

components, is actually quite limited. When q increases, the a

-constant in

the intra-industry oﬀ-diagonal terms are strongly suppressed with respect to

the equivalent term of size unity in the diagonal terms. Consequently, the

intra-industry correlation structure is distorted signiﬁcantly, and the two-

peak structure in the eigenvalue spectrum of C

(q)

(γ,δ; T ) is lost. Apparently,

q =1.5 is the optimal value for the power-mapping approach [120].

A variant of this model allows to perform a mean-ﬁeld analysis of the

correlations in a stock market [126]. The dynamical equation is written as

(t +1)=(1− 

− 

)[S

(t)+ε

(t)]





β=1



(t)+ε

(t)







γ∈g

(t)+ε

(t)] . (5.129)

N is the number of stocks in the market, and N

is the size of the industry

group which a particular stock belongs to. 

and 

are coupling constants

(weight factors) parameterizing the correlation of the price movement of the

stock S

with the market and the industry group. One important diﬀerence

to (5.123) is the explicit presence of the market mode. This is typical of

mean-ﬁeld approaches in statistical physics. Its appearence in (5.129) does

not have an immediate ﬁnancial interpretation. (However, one might think

about the benchmark-driven fund managers of today’s mutual fund industry.)

The other important diﬀerence to (5.123) becomes apparent when regrouping

the terms in (5.129) in a diﬀerent manner (we set 

= 0 for simplicity)

δS

(t)+

(t) −



γ∈g

(t)

= ε

(t) − 

(t) −



γ∈g

(t)

(5.130)

The coupling to the stocks of the same industry is implemented through the

diﬀerence terms which measure the deviation of the current stock price S

from the “industry mean-ﬁeld”

, and similarly for the price changes ε

The coupling to the market mode is realized with the same structure [126].

(5.129) can be rewritten as a continuity equation

δS

(t)=S(t +1)− S(t)=ε(t)+∆ ·[S(t)+ε(t)] . (5.131)

∆ = ∆

+ ∆

is a Laplace-type operator which describes ﬂows due to the

presence of gradients from the market and industry modes over an underlying

5.6 Non-Stable Scaling and Correlations in Financial Data 169

network. The gradients due to the intra-industry correlations are exhibited

by the diﬀerence terms in (5.130), and the gradients from market correlations

have similar structure. The elements of ∆

and ∆

are functions of 

and



, respectively [126]. The picture embedded is that of a network whose nodes

are formed by the labels of the stocks in the market, where a part of the price

changes is generated by ﬂows induced by the correlations.

Setting 

=0and

= 1 produces a mean-ﬁeld limit where the correla-

tion matrix can be calculated analytically. Its entries are [126]

C(γ,δ; T →∞)=

⎧

⎨

⎩

a(

)

[1 − a(

)] N + a(

)

if γ = δ

1ifγ = δ

(5.132)

with a(

)=

(3−2

)/(2−

). The largest eigenvector of this correlation

matrix

[1 − a(

)] N + a(

)

≈

2 − 

(1 − 

)

as N →∞. (5.133)

The eigenvalue of the market component diverges quadratically as the cou-

pling strength 

→ 1 in the large-N limit. This divergence, which is rem-

iniscent of critical phenomena as the fully correlated state is approached, is

conﬁrmed by numerical simulations. The actual position of the market eigen-

value can be used to calibrate the coupling constant 

of the model. When,

at the next stage, the industry groups and the coupling constants 

are de-

termined, one obtains good ﬁts to the eigenvalue spectra shown in Fig. 5.27.

In particular, the ﬁts produce the very large market eigenvector λ

, several

large eigenvalues due to industry correlations above the spectral range of ran-

dom matrix theory, and signiﬁcant spectral weight at or below the lower edge

of the random matrix theory spectrum [126]. As has been shown above based

on the model (5.123), this weight is the necessary counterpart to the large

intra-industry eigenvalues. Based on the eigenvalues, a rather detailed picture

of correlations and industry groups for ﬁnancial markets can be derived.

Approaches developed for cross-correlations in markets can also be adap-

ted to search for temporal correlation structures in one time series [124, 127].

Take a high-frequency time series of the DAX such as that shown in Fig.

5.5, and transform to normalized returns, (5.2). Now divide the history into

N days, and let T denote the length of the intraday time series recorded in

15-second intervals. One now can form a correlation matrix C(n

)where

denotes the n

th day of the history. Averaging is done over the intraday

recordings. C(n

) = 1 would imply that the time series of days n

and n

were identical. Of course, C again is a random matrix, and one can proceed

as above.

From about three years of DAX high-frequency data a spectrum quite

similar to Fig. 5.27 is found where two eigenvalues of the order 4 fall outside

the spectrum of random matrix theory, and are thus statistically signiﬁcant