Voit J. The Statistical Mechanics of Financial Markets

Подождите немного. Документ загружается.

140 5. Scaling in Financial Data and in Physics

on the depth of the traps. In this way, the energetic disorder of the intra-

gap impurity states generates, in a phenomenological perspective, a waiting

time distribution for the electrons in the traps. In a random walk, the walker

moves at every time step. In a biased random walk, underlying Gaussian

transport, there is an asymmetry of the probabilities of the right and left

moves which, again, take place at every time step. In dispersive transport,

particles do not move at every step. Their motion is determined, instead, by

their waiting time distribution. A shapshot of the electron density will now

show a strongly distorted proﬁle with a ﬂat leading and a steep trailing edge.

Only a few electrons have traveled very far, and many of them are still stuck

close to the origin. The current–time curves are now composed of two power

laws whose crossover deﬁned the transit time

I(t) ∼



−(1−α)

for t<t

−(1+α)

for t>t

(5.73)

The exponent α ∈ (0, 1) depends on the waiting time distribution of the

electrons in the traps, and hence on the disorder in the material.

Current–time proﬁles in agreement with (5.73) have indeed been measured

in the discotic liquid crystal system hexapentyloxytriphenylene (HPAT) [84].

The data show the characteristic structure of dispersive transport, with a

power-law decay of the displacement currents. Notice, however, that the ex-

ponents are such that the motion is subdiﬀusive, i.e., slower than for Gaussian

transport. This is a consequence of the existence of deep traps.

Glasses are another class of materials where disorder is, perhaps, the fac-

tor most inﬂuencing the physical properties. Experimentalists now are able

to measure the spectral (optical) lineshape of a single molecule embedded in

a glass. This lineshape sensitively depends on the interaction of the mole-

cule with its local environment and on the dynamical properties of the envi-

ronment. When many guest molecules are implanted in a glassy host, their

respective lineshapes all diﬀer due to their diﬀerent local environments. A

statistical analysis of the lineshapes becomes mandatory.

The lineshape of a single molecule may be described in term of its cumu-

lants, (5.17), in complete analogy to the description of a probability density

function through its cumulants in Sect. 5.4. When the cumulants of many

spectral lines are put together, one may determine the probability distri-

bution of each cumulant. In a simulation of several thousand molecules of

terylene embedded in polystyrene, one ﬁnds that the ﬁrst cumulant of the

lineshapes is distributed according to a symmetric Lorentz–Cauchy distri-

bution, the second cumulant according to a stable L´evy distribution with

µ =1/2 and a skewness β = 1 (a maximally skew distribution deﬁned for

positive values of the argument only), the third cumulant is drawn from a

symmetric L´evy distribution with µ =1/3, and the fourth cumulant is drawn

from an asymmetric distribution with skewness β =0.61 and index µ =1/4

[85].

5.5 Scaling, L´evy Distributions, and L´evy Flights in Nature 141

Another theoretical formulation of the spectral lineshapes of molecules

embedded in glasses may even be applied rather straightforwardly to the sta-

tistical properties of ﬁnancial time series [86, 87]. Physically here, each host

molecule in the neighborhood of the guest is assumed to shift the guest’s

delta-function absorption line depending on the individual host–guest inter-

action by a frequency ˜ν(R

). The total lineshape of the molecule then is the

superposition of these contributions. The two important factors determining

the lineshape are the distance dependence of the host–guest interaction and

the density of host molecules around one guest molecule. When the latter is

large, a Gaussian lineshape invariably follows. There are so many host mole-

cules around a guest molecule that simply the central limit theorem applies

and the details of the interaction process are not sampled in the lineshape.

On the other hand, when the density is small, the lineshape sensitively de-

pends on the dependence of the interaction on the spatial separation. With

˜ν(R

) ∼ R

−3/µ

, a stable L´evy-like lineshape obtains. We come back to this

theory in Chap. 6.

5.5.6 Superposition of Chaotic Processes

L´evy distributions can be generated by superposing speciﬁc chaotic processes

[88]. Chaotic processes are deﬁned by non-linear mappings of a variable X

n+1

= f (X

) , (5.74)

and are often used to model non-linear dynamical systems. If the mapping

function

f(X



−



(5.75)

is used in (5.74), and many processes corresponding to diﬀerent initial con-

ditions of the variable X are superposed, the probability distribution of the

variable X iterated and superposed in this way will converge to

p(X) →

π(1 + X

)

, (5.76)

that is, the Lorentz–Cauchy distribution. This is a special L´evy distribu-

tion with µ = 1. More general L´evy distributions can be obtained from the

mapping function

f(X





−





1/α

sign



−



. (5.77)

If this mapping is iterated, and many processes corresponding to diﬀerent

initial conditions are superposed, the probability density of X converges to

p(X) →

|X|

α−1



1+|X|

2α



, (5.78)

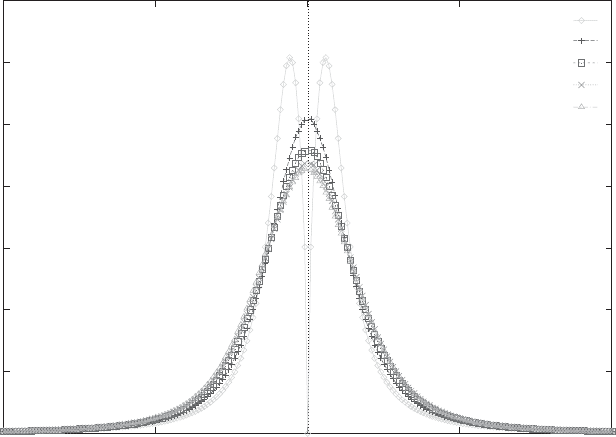
which has L´evy behavior with µ = α. This is shown in Fig. 5.20.

142 5. Scaling in Financial Data and in Physics

-10 -5 0 5 10

N=1

N=10

N=100

N=1000

N=10000

0.05

0.1

0.15

0.2

0.25

0.3

0.35

Fig. 5.20. Superposition of many chaotic processes, as described in the text. α =

3/2 has been used, and N denotes the number of processes with diﬀerent initial

conditions. By courtesy of K. Umeno. Reprinted from K. Umeno: Phys. Rev. E 58,

2644 (1998),

1998 by the American Physical Society

5.5.7 Tsallis Statistics

There are many properties which the Gaussian and the stable L´evy distri-

butions share: both are ﬁxed points, or attractors, for the distributions of

sums of independent random variables, in both cases guaranteed by a cen-

tral limit theorem, and both of them describe the probability distributions

associated with certain stochastic processes. The main diﬀerence is that the

Gaussian distribution is of ﬁnite variance, while the power-law decay of the

L´evy distributions leads to inﬁnite variance.

From a physics perspective, we could derive the Gaussian distribution

from a maximization of the entropy, subject to constraints, cf. Sect. 5.4.2. Is

it possible to generate stable L´evy distributions in a similar way?

There are two possibilities for achieving this. One is to keep the deﬁni-

tion of the Boltzmann–Gibbs entropy, (5.36), unchanged but to introduce a

constraint diﬀerent from (5.37) for the variance of the distribution function.

This requires rather complicated constraints. The alternative is to change the

deﬁnition of the entropy. It also requires a change of the variance constraint,

but a rather simple one only. This is the way taken by Tsallis et al. [77, 89].

They generalize the entropy to

5.5 Scaling, L´evy Distributions, and L´evy Flights in Nature 143

[p(x)] = k

1 −

∞

−∞





[σp(x)]

q − 1

. (5.79)

This reduces to the familiar Boltzmann–Gibbs entropy (5.36) in the limit q →

1. The probability distribution of the variable x characterizing the equilibrium

state of maximal entropy can then be determined by maximizing S[p] subject

to the constraints



∞

−∞

dxp(x)=1, x





∞

−∞





[σp(x)]

= σ

, (5.80)

generalizing (5.37). With these generalizations, one can essentially derive the

thermodynamic relations, such as T

−1

= ∂S/∂U, but the thermodynam-

ics and statistical mechanics are no longer extensive. This has given rise to

the name of “non-extensive statistical mechanics”, an area of rather intense

research currently.

The probability distributions maximizing S now depend on q.Forq ≤ 5/3,

the Gaussian obtains. For 5/3 <q<3, one ﬁnds the stable L´evy distributions

with index µ =(3−q)/(q −1) varying from 2 to zero as q increases from 5/3

to 3. For q>3, there is no solution [77, 89].

The stationary probability distributions obtained in this way are

(x)=



1 −

β(1 −q)U(x)



1/(1−q)

, (5.81)

where

β =1/k

T is the inverse temperature, Z

is the partition function,

and U(x) is a “potential” [90]. The label “potential” is to be taken in a

generalized sense which is explained below.

One may now ask: what dynamics equations could lead to such station-

ary distributions? The question can be posed at a macroscopic level, i.e.,

how must the evolution equation of p

(x) be structured in order to produce

stationary solutions of the form (5.81)? In ordinary Boltzmann–Gibbs sta-

tistical mechanics, this is the question about the appropriate Fokker–Plank

equation. One could also search for time-dependent solutions of these Fokker–

Planck equations, but we will not pursue this further here. On the other hand,

one can ask for the evolution equation for the stochastic variable, i.e., take

a microscopic view. This is the question for the appropriate Langevin-type

equation.

We ﬁrst turn to the macroscopic level. In ordinary statistical physics for

Markov processes, the evolution of the probability density function is gov-

erned by a Fokker–Planck equation

∂p(x, t)

∂t

= −

∂

∂x



(1)

(x, t)p(x, t)



∂

∂x



(2)

(x, t)p(x, t)



, (5.82)

where D

(1)

and D

(2)

are the drift and diﬀusion “coeﬃcients”, respectively.

For constant D

(2)

and time-independent D

(1)

(x), the stationary solution is

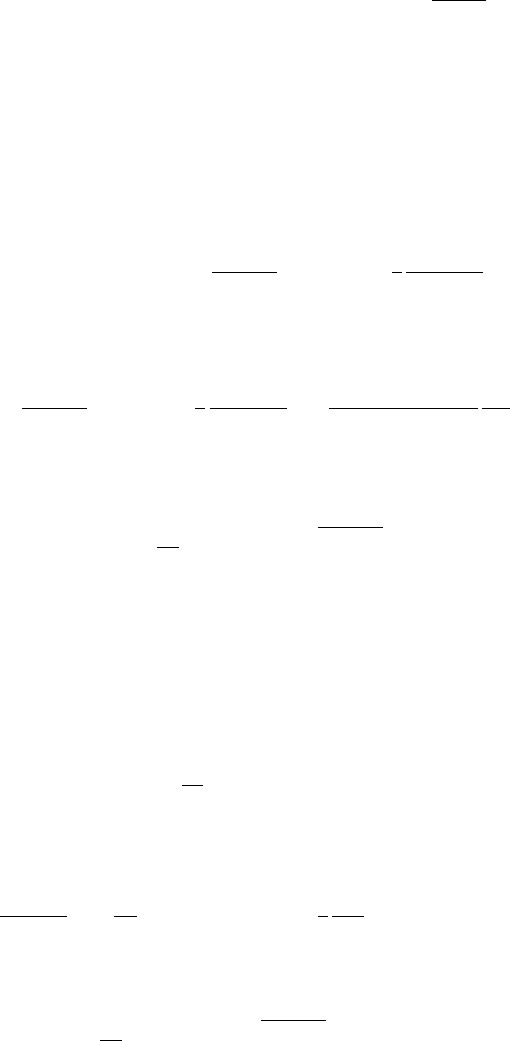
144 5. Scaling in Financial Data and in Physics

p(x)=N exp



−

βU(x)



with D

(1)

(x)=−

∂U(x)

∂x

. (5.83)

N is a normalization factor. The “potential” is thus deﬁned via the drift

coeﬃcient D

(1)

. The drift is a result of a force acting on the particles.

In the macroscopic view of non-extensive statistical mechanics, one can

imagine arriving at (5.81) either from a Fokker–Planck equation linear in the

probability density p

(x), such as the preceding one [91], or one containing

non-linear powers of p

(x) [92]. In the linear framework, our approach is to

derive special relations between D

(1)

(x)andD

(2)

(x) by equating the general

stationary solution of the Fokker–Planck equation [37]

p(x)=N exp





(2)

(x)



(1))

(x) −

∂D

(2)

(x)

∂x



(5.84)

with the stationary distribution (5.81) obtained from entropy maximization

[91]. This equation is solved when the condition

(2)

(x)



(1)

(x) −

∂D

(2)

(x)

∂x



−

1 −

β(1 −q)U(x)

∂U

∂x

(5.85)

is satisﬁed, where U (x) is deﬁned in (5.83). On the other hand, a Fokker–

Planck equation implies a Langevin equation for the evolution of the stochas-

tic variable [37]

= D

(1)

(x)+

(2)

(x)η(t) , (5.86)

where η(t) is white noise. For any given U(x), (5.85) thus determines a family

of microscopic Langevin equations which give rise to non-extensive statistical

mechanics on the macroscopic level [91]. It is the special interplay of the

deterministic drift D

(1)

and the stochastic diﬀusion coeﬃcients D

(2)

which

determines the steady-state distribution of the system, and not so much the

particular form of the coeﬃcients.

Using (5.81), (5.85) can be rewritten as

= −

β(Z

)

q−1

U(x)dx, (5.87)

which is identical to the stationary solution of non-linear Fokker–Planck equa-

tions. The non-linear Fokker–Planck equation is [92]

∂f(x, t)

∂t

= −

∂

∂x



(1)

(x)f

(x, t)



∂

∂x



(2)

(x)f

(x, t)



. (5.88)

ν and ρ are real numbers characterizing the non-linearity. This equation is

equivalent to a Langevin equation

= D

(1)

(x)+

(2)

(x)f(x, t)

(ν−ρ)/2

η(t) . (5.89)

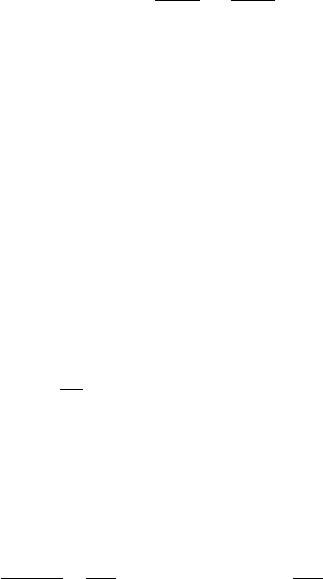
5.5 Scaling, L´evy Distributions, and L´evy Flights in Nature 145

Here, f(x, t) is an auxiliary distribution and not the physical probability

distribution p(x, t). The physical distribution is p(x, t)=f

(x, t).

The important feature of (5.89) is the dependence of the eﬀective dif-

fusion coeﬃcient D

(2)

(ν−ρ)/2

acting on the microscopic level on the prob-

ability density f

(ν−ρ)/2

= p

(ν−ρ)/2ρ

realized at the macroscopic level [92].

The non-linear Fokker–Planck equation (5.88) and the Langevin equation

(5.89) no longer are equivalent, complementary descriptions of a stochastic

system but here turn into a system of coupled equations. The feedback of

the macroscopic into the microscopic level apparently is the prerequisite to

turn ordinary Boltzmann–Gibbs statistical mechanics into non-extensive sta-

tistical mechanics. When an interpretation in terms of Brownian motion is

sought, one would conclude that the amplitude of the shocks the Brownian

particle picks up from its environment depends on the frequency of its visits

to speciﬁc regions of space. This might lead to a cleaving of phase space.

The scaling properties of the variance of the system variable

x

(bt) = b

2/(3−q)

x

(t) with

1 − ν

1+ν

q − 1

3 − q

at ρ = 1 (5.90)

demonstrate that non-extensive statistical mechanics describes anomalous

diﬀusion [92]. This equation suggests that the Hurst exponent H of this sys-

tem is H =1/(3 −q). It might even suggest that the processes are related to

fractional Brownian motion, (4.42). When the Hurst exponent is calculated in

the way it was originally deﬁned [33], one ﬁnds, however, that, for the anom-

alous diﬀusion described in non-extensive statistical mechanics, the Hurst

exponent is H =0.5 as for ordinary Brownian motion and independent of q

while, for fractional Brownian motion, it is diﬀerent. The underlying reason

is that the stochastic process of non-extensive statistical mechanics described

by (5.89) is uncorrelated in time. Fractional Brownian motion, (4.42), on the

other hand, possesses long-range temporal correlations which are at the origin

of the non-trivial Hurst exponent.

A less formal and more intuitive approach starts from the ordinary

Langevin equation

= −γx + ση(t) . (5.91)

The identiﬁcation with (5.86) is made through D

(1)

(x)=−γx and D

(2)

(x)=

. Our emphasis here is not on the dependences of the drift and diﬀu-

sion coeﬃcients on the stochastic variable but rather on the possibility that

they slowly ﬂuctuate in time. A speciﬁc assumption is that β = γ/σ

-distributed with degree n [93], i.e., that

p(β)=

Γ (n/2)



2β



n/2

n/2−1

exp



−

nβ

2β



. (5.92)

A variable which is the sum of the squares of n Gaussian distributed random

variables is distributed according to a χ

-distribution of degree n. β

= β

is the average of β.

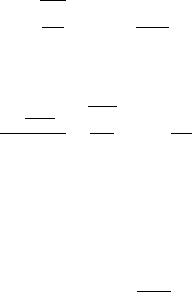
146 5. Scaling in Financial Data and in Physics

If the time scale on which β ﬂuctuates is much longer than 1/γ,thetime

scale of the stochastic variable, the conditional probability of x on β,is

p(x|β)=



2π

exp



−

βx



. (5.93)

The marginal probability of x then is

p(x)=



p(x|β)p(β)dβ =

Γ (

n+1

)

Γ (n/2)



πn





−(n+1)/2

. (5.94)

Comparison with (5.81) shows that the distribution found for this system with

slowly ﬂuctuating drift and diﬀusion coeﬃcients is a stationary distribution of

non-extensive statistical mechanics provided one identiﬁes q =1+2/(n +1)

and

β =2β

/(3 − q). The potential is U(x)=x

/2, as appropriate for

ordinary diﬀusion. Also, p(x) is identical to a Student-t distribution, (5.59),

with index µ = n and scale parameter A =



n/β.

Non-linear Langevin equations may be studied in the same way. As ex-

pected from (5.82) with the potential U (x) deﬁned in (5.83), a power-law

dependence in the drift coeﬃcient will translate into a non-trivial power-law

dependence on x in the probability distribution. We postpone the applica-

tion of this theory to a physical example, hydrodynamic turbulence, and to

ﬁnancial markets, to the next chapter.

An aspect which has not been clariﬁed satisfactorily yet is the scope

of application of non-extensive statistical mechanics. Thermodynamics and

statistical mechanics usually treat systems in or close to equilibrium. The

experimental results discussed above, where L´evy-type scaling was found, to

a varying degree depart from equilibrium situations. The example of micelles

certainly is close to equilibrium, but the rotating ﬂuid containing jets and

vortices is a stationary state rather far away from equilibrium. What about

turbulence, the subject of the next chapter? And social systems or ﬁnancial

markets? Does the non-extensive statistical mechanics describe situations

both close to and far away from equilibrium? Where in the theory could we

nail down this opening to non-equilibrium physics? Attempts to answer these

questions are just beginning to appear [94]. The state of the art in this ﬁeld of

research is summarized in the proceedings of a conference on Tsallis statistics

[95].

5.6 New Developments: Non-stable Scaling, Temporal

and Interasset Correlations in Financial Markets

The assumption of statistical independence of subsequent price changes, made

by the geometric Brownian motion hypothesis, is apparently rather well sat-

isﬁed by stock markets, both concerning the decay of return correlation func-

tions, and the use of correlations in practical trading rules. On the contrary,

5.6 Non-Stable Scaling and Correlations in Financial Data 147

the distribution of returns of real markets is far from Gaussian, and Sect. 5.3.3

suggested that returns were drawn from distributions which either were sta-

ble L´evy distributions, or variants thereof with a truncation in their most

extreme tails.

5.6.1 Non-stable Scaling in Financial Asset Returns

There were, however, observations in the economics literature which could

raise doubts about the simple hypothesis of stable L´evy behavior. As an

example, it appeared that the L´evy exponent µ somewhat depended on the

time scale of the observations, i.e., if intraday, daily, or weekly returns were

analyzed [96]. This is not expected under a L´evy hypothesis because the

distribution is stable under addition of many IID random variables. Returns

on a long time scale obtain as the sum of many returns on short time scales,

and therefore must carry the same L´evy exponent.

Lux examined the tail exponents of the return distributions of the German

DAX stock index, and of the individual time series of the 30 companies

contained in this index by applying methods from statistics and econometrics

[97]. Interestingly, he found his results consistent with stable L´evybehavior

for the majority of stocks and for the DAX share index, with exponents in

the range µ ≈ 1.42,...,1.75.

A counter-check, using an estimator of the tail index introduced in

extreme-value theory, led to diﬀerent conclusions, however. It turned out

that all stocks, and the DAX index, were characterized by tail exponents

2 <µ≤ 4, i.e., outside the stable L´evy regime. In most cases, even the

95% conﬁdence interval did not overlap with the regime required for sta-

bility, µ ≤ 2. Moreover, statistical tests could not reject the hypothesis of

convergence to a power law.

The estimator used is more sensitive to extremal events in the tails of a

distribution than a standard power-law ﬁt. It deliberately analyzes the tail

of large events where, e.g., in the bottom panel of Fig. 5.10, deviations of the

data from L´evy power laws become visible. It would indicate that a power-

law tail with an exponent µ>2 is more appropriate than an exponential

truncation scheme.

These conclusions are corroborated by an investigation using both two

years of 15-second returns and 15 years of daily returns of the DAX index. The

corresponding price charts are given in Figs. 5.5 and 1.2. Figure 5.21 displays

the normalized returns of the DAX high-frequency data presented earlier,

in double-logarithmic scale [59, 60]. The ﬁgure is essentially independent of

whether positive, negative, or absolute returns are considered, and the last

possibility has been chosen. Again, we ﬁnd approximately straight behavior

for large returns, suggesting power-law behavior and fat tails.

Using the Hill estimator of extreme-value theory [98, 99] to estimate the

asymptotic distribution for |δs



|→∞, a tail index µ ≈ 2.33 for a power-law

distribution

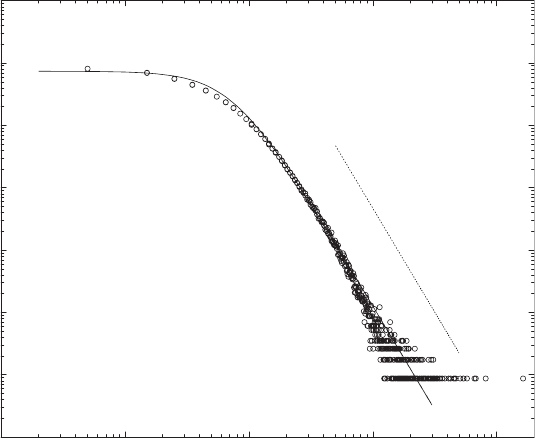
148 5. Scaling in Financial Data and in Physics

p(δs

) ∼|δs

−1−µ

(5.95)

is determined. This power law is shown as the dotted line in Fig. 5.21. The

solid line in Fig. 5.21 is a one-parameter ﬁt to a Student-t distribution (5.59),

where the exponent derived from the Hill estimator was taken ﬁxed and only

the scale parameter A of the distribution was ﬁtted. The index µ ≈ 2.33 is

signiﬁcantly bigger than Mandelbrot’s 1963 value and outside the range of

stable L´evy distributions, but roughly in line with Lux’s result using data on

a longer time scale [97].

Both the curvature of the data away from the straight line in Fig. 5.21

and the convergence, with a ﬁnite slope, of the Hill estimator to its inﬁnite

ﬂuctuation limit suggest that the probability distribution of extreme returns

is not a pure power law but rather contains multiplicative corrections vary-

ing more slowly than a power law. The existence of such (e.g., logarithmic)

corrections to power-law properties is well known in statistical physics in the

vicinity of critical points. The idea of slowly varying corrections to power laws

−2

−1

|δs|

−6

−5

−4

−3

−2

−1

P(δs)

µ=2.33

Fig. 5.21. Probability density function of 15-second DAX returns. The straight

dotted line indicates a power law with its index µ =2.33 derived from extreme-

value theory. The solid line is a ﬁt to a Student-t distribution using the exponent

determined independently. From S. Dresel: Modellierung von Aktienm¨arkten durch

stochastische Prozesse, Diplomarbeit, Universit¨at Bayreuth, 2001, by courtesy of

S. Dresel

5.6 Non-Stable Scaling and Correlations in Financial Data 149

1 10 100

Normalized S&P500 returns

−7

−6

−5

−4

−3

−2

−1

Cumulative distribution

Postive tail

Negative tail

Lévy Regime

µ ≈€1.7

µ ≈€3

µ = 2

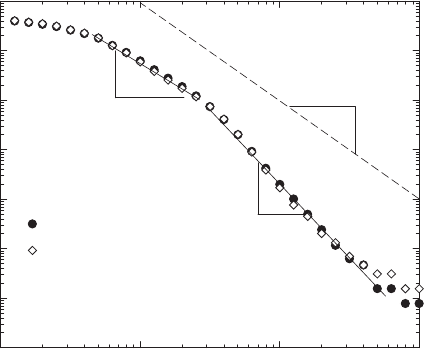
Fig. 5.22. Cumulative distribution function of normalized returns of the S&P500

share index. Three diﬀerent regimes can be distinguished: small returns much less

than a standard deviation, where no analysis was performed; an intermediate regime

of returns ≈ 0.4 ...3σ, where a stable L´evy power law is appropriate; and a large-

ﬂuctuation regime of power-law return with an exponent µ = 3 outside the stable

L´evy range.The dashed line µ = 2 is the limit of L´evy stability. By courtesy of P.

Gopikrishnan. Reprinted from P. Gopikrishnan et al.: Phys. Rev. E 60, 5305 (1999)

1999 by the American Physical Society

is already contained in work by Cont [100] and a recent paper by LeBaron

[101].

A tail exponent of µ = 3 is also found for other stock markets, such as

the S&P500, the Japanese Nikkei 225, and the Hong Kong Hang Seng indices

[62]. Figure 5.22 shows the cumulative probability

(δS)=



∞

δS

d(δS



) p(δS



) (5.96)

for the normalized returns of the S&P500 index. Clearly, the tails containing

the extreme events follow a power law

(δS) ∼ (δS)

−µ

(5.97)

with an exponent µ = 3, beyond the limit of stability of L´evy laws. However,

we also recognize that a stable L´evy law with µ =1.7 is a good description in

an intermediate range of returns 0.4σ ≤ δS ≤ 3σ. This power law had been

emphasized in earlier studies and was discussed in Sect. 5.3.3.

Tail exponents 2 <µ≤ 6 have also been found in a variety of other mar-

kets, most notably foreign exchange markets, interbank cash interest rates,