Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей

71

где

-

¢

A

диагональная матрица коэффициентов уравнений, полученная после n

преобразований в процессе прямого хода.

Окончательное решение может быть записано в виде

в

X

1

¢

=

×

,

где

-

¢

в

получается после умножения

в

¢

на матрицу

(

)

1

-

¢

A :

(

)

вAв

1

¢¢

=

¢¢

-

.

Для диагональной матрицы обратная также является диагональной; в диаго-

нали расположены коэффициенты, обратные коэффициентам исходной матрицы.

То есть последнюю операцию выполнить очень просто.

Если предположить, что нужно решить ряд систем уравнений с одной и той

же матрицей коэффициентов

A

и разными правыми частями, то в матричном виде

это можно представить следующим образом:

B

AX

=

,

или

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

333231

232221

131211

333231

232221

131211

333231

232221

131211

bbb

xxx

aaa

,

где

-

X

матрица неизвестных для каждой из систем;

-

B

матрица правых частей для каждой из систем.

Предположим, что матрица

X

представляет собой обратную матрицу по от-

ношению к матрице

A

, т. е.

1

-

=

A

X

.

Тогда для того, чтобы решение системы уравнений

B

AX

=

отвечало нахождению

матрицы

1

-

A

, матрица коэффициентов

B

должна представлять собой диагональ-

ную единичную матрицу:

1

AX

=

,

Тогда в матричном виде можно записать:

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

ú

û

ù

ê

ë

é

100

010

001

333231

232221

131211

333231

232221

131211

xxx

aaa

.

Решив эту систему методом Гаусса относительно Х, получим матрицу

1

-

A

.

Рассмотрим метод на примере системы из трех уравнений:

.

3333232131

2323222121

1313212111

bxaxaxa

=++

=

+

72

Запишем матрицу коэффициентов А и единичную матрицу В того же порядка, что

и матрица А:

ú

û

ù

ê

ë

é

=

333231

232221

131211

aaa

А ;

ú

û

ù

ê

ë

é

=

100

010

001

В .

Будем выполнять операции по методу Гаусса одновременно с обеими мат-

рицами, используя соответствующие коэффициенты преобразований, найденные

для матрицы коэффициентов А.

Первый шаг:

()

(

)

(

)

() ()

ú

û

ù

ê

ë

é

=

1

33

1

32

1

23

1

22

1

13

1

12

0

1

aa

1

А

;

()

(

)

()

ú

û

ù

ê

ë

é

=

10

01

00

1

31

1

21

1

11

b

1

В

.

Второй шаг:

()

(

)

()

ú

û

ù

ê

ë

é

=

2

33

2

23

2

13

00

10

01

a

2

А

;

()

(

)

(

)

() ()

ú

û

ù

ê

ë

é

=

1

0

2

32

2

31

2

22

2

21

2

12

2

11

bb

2

В

.

Третий шаг:

()

ú

û

ù

ê

ë

é

=

100

010

001

3

А ;

()

(

)

(

)

(

)

() () ()

ú

û

ù

ê

ë

é

=

3

33

3

32

3

31

3

23

3

22

3

21

3

13

3

12

3

11

bbb

3

В

.

Полученная матрица

(

)

3

В

удовлетворяет условию

1

=

AX

, следовательно

1

A

X

-

=

и

(

)

13

A

B

-

=

, т.е.

(

)

-

3

B

матрица, обратная к

A

.

Для иллюстрации методики рассмотрим обращение матрицы коэффициен-

тов системы уравнений

2

932

4

321

-=--

=++

=

+

xxx

Запишем матрицу коэффициентов

A

и единичную диагональную матрицу

B

третьего порядка:

ú

û

ù

ê

ë

é

--

=

111

132

111

А ;

ú

û

ù

ê

ë

é

=

100

010

001

В .

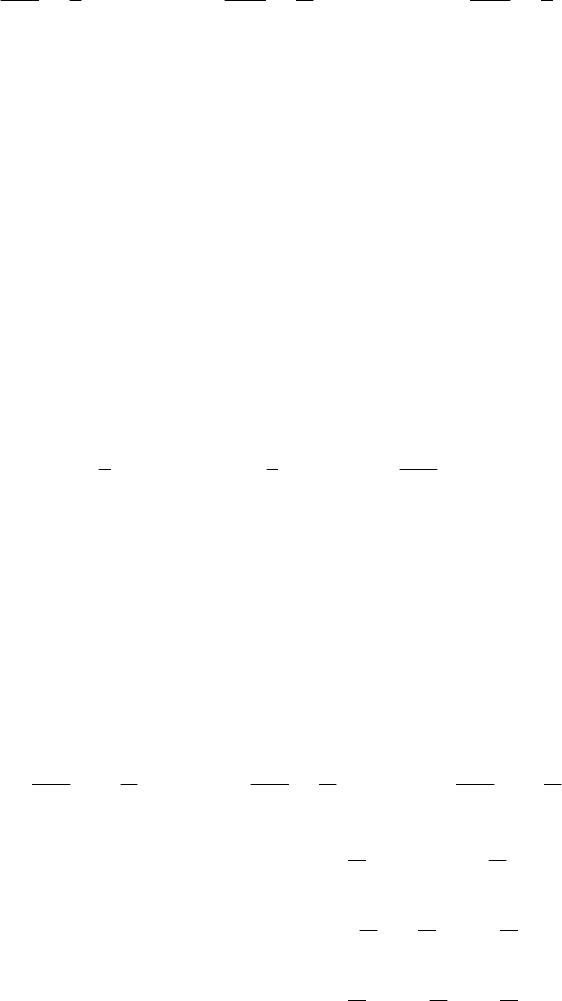
73

Первый шаг. Найдем коэффициенты преобразования уравнений:

()

1

11

1

===

a

m ;

()

2

1

2

11

21

1

2

===

a

m ;

()

1

11

31

1

3

===

a

m

Умножим коэффициент

(

)

1

2

m на первое уравнение и результат умножения

вычтем из второго уравнения. Эту же операцию проведем с элементами матрицы,

стоящей справа. Умножим коэффициент

(

)

1

3

m на первое уравнение и результат ум-

ножения вычтем из третьего уравнения. Аналогично поступим с элементами мат-

рицы, стоящей справа. В результате получим:

()

ú

û

ù

ê

ë

é

--

-=

220

110

111

1

А ;

()

ú

û

ù

ê

ë

é

-

-=

101

012

001

1

В .

Второй шаг. Найдем коэффициенты преобразования уравнений:

()

;m 1

1

2

1

==

()

;m

1

2

=

()

2

1

2

3

-=

-

=m

После преобразований, аналогичных выполненным на первом шаге, полу-

чим:

()

ú

û

ù

ê

ë

é

-

-=

400

110

201

2

А ;

()

ú

û

ù

ê

ë

é

-

=

125

012

013

2

В .

Третий шаг выполняется аналогично первому и второму:

()

;m

2

1

4

2

3

1

-=

-

=

()

;m

4

1

4

1

3

2

=

-

=

()

4

1

4

1

3

-=

-

=m

()

ú

û

ù

ê

ë

é

=

100

010

001

3

А ;

()

ú

û

ù

ê

ë

é

--

--=

4

1

2

1

4

5

4

1

2

1

4

3

2

1

0

2

1

3

В .

Таким образом,

(

)

3-1

В

А

=

.

Умножив обратную матрицу на столбец правых частей, найдем искомые неиз-

вестные:

74

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

-

×

ú

û

ù

ê

ë

é

--

--=

ú

û

ù

ê

ë

é

1

2

1

2

9

4

1

2

1

4

5

4

1

2

1

4

3

2

1

0

2

1

3

2

1

x

.

4.4.3. Обращение матрицы коэффициентов методом перестановки столбцов

По сути этот метод аналогичен методу Гаусса, т.к. в его основе также зало-

жено исключение неизвестных из уравнений.

Если в системе уравнений

в

AX

=

найти способ переставить

X

и

в

местами, так, чтобы:

XQb

=

,

то в этом случае:

1

AQ

-

= и

в

A

X

1-

=

.

Методика получения обратной матрицы состоит в следующем: в процессе

преобразований последовательно каждое из уравнений разрешается относительно

“своего” неизвестного. При этом коэффициент

b

этого уравнения переходит в ле-

вую часть, а неизвестное

-

X

в правую. Затем разрешенное относительно неиз-

вестного уравнение подставляется во все другие уравнения. После преобразования

таким образом всех уравнений получим систему, в правой части которых оказыва-

ется столбец

X

, а коэффициенты при

i

b оказываются коэффициентами обратной

матрицы по отношению к исходной матрице коэффициентов.

Поясним алгоритм нахождения обратной матрицы этим способом на приме-

ре системы из трех уравнений.

Первый шаг: в исходной системе уравнений

,

3333232131

2323222121

1313212111

bxaxaxa

=++

=

+

разрешим первое уравнение относительно неизвестного

1

x и выражение для

1

x

подставим во второе и третье уравнения:

(

)

(

)

(

)

() () () ()

1

3

1

33

2

1

32

1

31

1

2

3

1

23

2

1

22

1

21

13

1

13

2

1

12

1

11

bxaxaba

xxaxaba

=++

,

где

()

() ()

;;;

1

11

13

1

13

11

12

1

12

11

1

11

a

a -=-==

75

() () ()

;;;

11

13

2123

1

23

11

12

2122

1

22

11

21

1

21

a

aaa

a

aaa

a

a ×-=×-==

()

() ()

.;;

11

13

3133

1

33

11

12

3132

1

32

11

31

1

31

a

aaa

a

aaa

a

a -=-==

В матричном виде можно записать:

(

)

(

)

(

)

() () ()

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

3

2

1

3

2

1

33

1

32

1

31

1

23

1

22

1

21

1

13

1

12

1

11

b

x

b

aaa

.

Второй шаг: произведем аналогичную операцию, но главным в этом случае

будет второе уравнение. Разрешим это уравнение относительно неизвестного

2

x и

после преобразования подставим

2

x в первое и третье уравнения. После приведе-

ния подобных получим следующее матричное выражение:

(

)

(

)

(

)

() () ()

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

3

2

1

3

2

1

2

33

2

32

2

31

2

23

2

22

2

21

2

13

2

12

2

11

b

x

b

aaa

.

Третий шаг выполняется совершенно аналогично, то есть третье уравнение

разрешим относительно неизвестного

3

x и подставим

3

x в первое и второе урав-

нения.

В результате получим:

(

)

(

)

(

)

() () ()

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

3

2

1

3

2

1

3

33

3

32

3

31

3

23

3

22

3

21

3

13

3

12

3

11

x

b

aaa

.

Формулы преобразования имеют удобную структуру и легко программируются.

Поясним рассмотренный алгоритм на примере системы из трех уравнений:

.2

932

4

321

-=--

=++

=

+

xxx

Вместо правых частей введем формальные переменные

3

2

1

b,b,b :

.

32

3321

2321

1321

bxxx

=--

=++

=

+

Разрешим первое уравнение системы относительно неизвестного

1

x и под-

ставим выражение для

1

x во второе и третье уравнения:

76

.22

2

3321

2321

1321

bxxb

xxxb

=--

=-+

=

-

Разрешим второе уравнение полученной системы относительно неизвестного

2

x и выражение для

2

x подставим в первое и третье уравнения:

.425

2

23

3321

2321

1321

bxbb

xxbb

=--

=++-

=

-

Третий шаг выполняется аналогично:

.25,05,025,1

25,05,075,0

5,005,0

3321

2321

1321

xbbb

=--

=-+-

=

+

-

Таким образом,

1

-

А

25050251

25050750

50050

,,,

,,

--

--= .

Для нахождения неизвестных умножим полученную обратную матрицу на столбец

правых частей:

Х

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

-

×

ú

û

ù

ê

ë

é

--

--=

1

2

1

2

9

4

25,05,025,1

25,05,075,0

5,005,0

.

Для оценки эффективности рассмотренных методов обращения матриц

нужно вычислить общее количество операций умножения и деления.

При применении для обращения матрицы коэффициентов метода Гаусса без

обратного хода и метода перестановки столбцов число операций умножения и де-

ления составляет

3

n

. Если рассмотреть классический метод обращения матрицы,

то при этом необходимо вычислить

2

n

определителей

(

)

1

-

n порядка и один опре-

делитель n порядка. Вычисление определителя порядка n требует число операций:

(

)

(

)

3

31

2

++- nnn

.

Учитывая число вычисляемых определителей, нетрудно определить, что ме-

тод Гаусса и метод перестановки столбцов являются более экономичными.

Допустим, что необходимо решить

m

систем уравнений, у которых имеется

одна и та же матрица коэффициентов А, а отличие состоит лишь в различных ко-

эффициентах правых частей в.

При использовании методов обращения матриц (Гаусса и перестановки

столбцов) общее число операций умножения и деления

3

n

будет соответствовать

однократному обращению матрицы коэффициентов и

-

m

кратному перемноже-

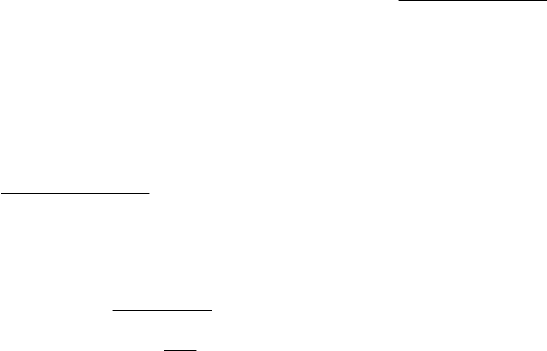
77

нию матрицы

1

-

А

на столбец коэффициентов в, которое в свою очередь состав-

ляет

2

n

операций умножения. То есть общее количество операций будет равно

23

n

m

n

×

+

.

Число операций, которое необходимо выполнить при использовании для

решения уравнений метода Гаусса с обратным ходом как самого экономичного

среди численных методов, можно определить по выражению

(

)

m

nnn

×

ú

û

ù

ê

ë

é

-+

3

13

2

.

Определим, при каком числе

m

использования обратной матрицы для полу-

чения решения метод обращения матрицы более эффективен, чем метод Гаусса,

то есть

(

)

23

2

3

13

nmn

nnn

m ×+³

ú

û

ù

ê

ë

é

-+

.

После преобразований получим:

÷

ø

ö

ç

è

æ

-

³

2

1

3

n

m .

Расчеты по данному выражению показывают, что рассмотренные методы

обращения матриц оказываются более эффективными, если они используются для

одновременного получения числа решений

m

, большего 4. Однако, с учетом осо-

бенностей матриц коэффициентов уравнений состояния электрической сети, в ча-

стности, их разряженности (большое количество нулевых элементов), а также

симметричности, преимущество применения обратных матриц даже при много-

кратном их использовании становится не столь очевидным, поскольку метод Га-

усса позволяет учесть эти особенности матриц коэффициентов путем создания ал-

горитмов, предусматривающих операции только с ненулевыми элементами с уче-

том симметрии матриц.

4.4.4. Получение обратной матрицы методом факторизации

Стандартные методы обращения матриц, традиционно применяемые в вы-

числительной математике, не позволяют учесть особенности электротехнических

задач, в частности, симметрию коэффициентов системы уравнений относительно

главной диагонали и разряженность матриц коэффициентов, что снижает эффек-

тивность применения обратных матриц по сравнению с методом Гаусса с обрат-

ным ходом, даже если обратная матрица применяется многократно. Желание

учесть особенности электротехнических задач при обращении матриц привело к

разработке метода факторизации, суть которого состоит в том, что каждый шаг

преобразования методом Гаусса представляется как произведение нижних или

верхних треугольных матриц на преобразованную матрицу коэффициентов А. Са-

78

ми треугольные матрицы, по существу, заполняются коэффициентами преобразо-

вания по методу Гаусса на каждом шаге. Таким образом, метод факторизации –

это матричная реализация метода Гаусса. Так как коэффициенты преобразования

на каждом шаге для каждого уравнения в числителе имеют коэффициент, кото-

рый должен быть обнулен, то при записи матриц – сомножителей автоматически

учитывается разряженность матрицы коэффициентов, так как при наличии в чис-

лителе нулевого элемента коэффициент преобразования оказывается нулевым.

Рассмотрим алгоритм на примере матрицы третьего порядка.

Запишем на прямом ходе преобразования матрицы

А

ú

û

ù

ê

ë

é

=

333231

232221

131211

aaa

методом Гаусса исключение всех элементов ниже первого главного диагонально-

го элемента в матричной форме. Для этого составим нижнюю треугольную мат-

рицу, в диагонали которой будут стоять единицы, все элементы выше диагонали

равны нулю, все элементы ниже диагонали, кроме первого столбца, также равны

нулю. В первый столбец поместим коэффициенты преобразований с обратным

знаком:

(

)

1

L

ú

û

ù

ê

ë

é

-

-=

10

01

001

11

31

11

21

а

.

Умножим матрицу

A

слева на матрицу

(

)

1

L

:

(

)

1

A

=

(

)

А

L

×

1

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

-

-=

333231

232221

131211

11

31

11

21

10

01

001

aaa

a

(

)

(

)

(

)

() ()

ú

û

ù

ê

ë

é

1

33

1

32

1

23

1

22

1

13

1

12

1

11

0

aa

aaa

.

Выполним аналогичное матричное преобразование

(

)

1

A

, эквивалентное

преобразованию этой матрицы на втором шаге преобразования по методу Гаусса.

Для этого матрицу

(

)

1

A

умножим слева на второй матричный сомножитель

(

)

2

L

,

представляющий собой нижнюю треугольную матрицу, построенную аналогично

матрице

(

)

1

L

, при этом коэффициент преобразования помещается во втором

столбце ниже главной диагонали:

79

(

)

(

)

(

)

А

L

А

122

×

=

()

() () ()

() ()

() () ()

() ()

()

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

-

=

2

33

2

23

2

22

2

13

2

12

2

11

1

33

1

32

1

23

1

22

1

13

1

12

1

11

1

22

1

32

00

0

10

010

001

a

aa

aaa

aa

aaa

a

.

Если число преобразуемых уравнений равно n, то после (n-1) преобразования (ум-

ножение на матрицы – сомножители) получим следующее выражение:

(

)

(

)

(

)

(

)

1121

-

=

×

nnn

A

L

K

. (4.8)

Если перемножить все сомножители, то получим некоторую матрицу

L

, все

элементы ниже главной диагонали которой равны коэффициентам преобразова-

ний, взятым с обратным знаком.

(

)

(

)

(

)

121

L

nn

×

=

-

K

(4.9)

Для системы третьего порядка можно записать:

L

ú

û

ù

ê

ë

é

--

-=

1

01

001

3231

21

ll

l .

Выполним второй этап в матричном виде. Суть его заключается в том, что-

бы обнулить в матрице

(

)

1

-

n

A

все элементы, стоящие выше диагонали. Для удоб-

ства преобразований переобозначим матрицу

(

)

2

A

:

(

)

2

H

=

(

)

(

)

(

)

() ()

()

(

)

(

)

(

)

() ()

()

ú

û

ù

ê

ë

é

=

ú

û

ù

ê

ë

é

2

33

2

23

2

22

2

13

2

12

2

11

2

33

2

23

2

22

2

13

2

12

2

11

00

0

00

0

a

aa

aaa

h

hh

hhh

.

Умножим матрицу

(

)

2

H

на верхнюю треугольную матрицу

(

)

2

Q , в диагонали

которой находятся единицы, все элементы ниже главной диагонали равны нулю,

элементы выше главной диагонали, кроме элементов последнего столбца, также

равны нулю. В последний столбец поместим коэффициенты преобразования по

методу Гаусса, вычисляемые аналогично описанному выше. При таком перемно-

жении выполняется операция обнуления элементов последнего столбца матрицы

(

)

2

H

, стоящих выше диагонали.

Запишем коэффициенты преобразований:

()

(

)

()

2

33

2

13

2

13

h

q = ;

()

(

)

()

2

33

2

23

2

23

h

q = .

После перемножения получим:

80

(

)

(

)

(

)

=×=

22

HQH

1

(

)

()

() () ()

() ()

()

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

-

2

33

2

23

2

22

2

13

2

12

2

11

2

33

2

23

2

33

2

13

00

0

100

10

01

h

hh

hhh

h

(

)

(

)

()

ú

û

ù

ê

ë

é

1

33

1

22

1

12

1

11

00

0

h

hh

.

Следующий шаг преобразования заключается в аналогичной операции, ко-

торая должна закончиться исключением всех значащих элементов во втором

столбце выше главной диагонали. Для этого умножим слева

(

)

1

H

на верхнюю тре-

угольную матрицу, в которой записаны только элементы второго столбца выше

главной диагонали:

Н

=

(

)

×

1

Q

(

)

1

H

(

)

()

() ()

()

=

ú

û

ù

ê

ë

é

×

ú

û

ù

ê

ë

é

-

=

1

33

1

22

1

12

1

11

1

22

1

12

00

0

000

010

01

h

hh

h

ú

û

ù

ê

ë

é

33

22

11

00

h

;

В общем случае можно записать:

(

)

(

)

(

)

(

)

(

)

(

)

(

)

1n-----

×=×=××××× AQHQHQQQQ

1n1n1n2n21

K

, (4.10)

где для системы третьего порядка Q

ú

û

ù

ê

ë

é

-

--

=

100

10

1

23

1312

q

qq

.

В матричном виде можно записать:

(

)

A

L

A

n

×

=

-

1

; (4.11)

HALQ

=

×

. (4.12)

Умножая (4.12) последовательно на

-1

Q и

-1

L

слева для разрешения относитель-

но

A

, получим:

HQLA ××=

-

11

. (4.13)

Тогда выражение для обратной матрицы можно записать в виде:

LQНА ××=

-

11

(4.14)

Так как

H

является диагональной матрицей, то обращение матрицы

A

сво-

дится к обращению этой диагональной матрицы и ее умножению на две треуголь-

ные матрицы – верхнюю и нижнюю. Обращение диагональной матрицы не со-

ставляет затруднений. Коэффициенты треугольных матриц Q и

L

получаются

фактически при обычной реализации метода Гаусса.

Достоинство этой формы получения обратной матрицы состоит в следую-

щем:

Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей

Подождите немного. Документ загружается.