Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей
Подождите немного. Документ загружается.

11
требуют значительных вычислительных затрат, особенно для ЭЭС большой слож-
ности.
В связи с отмеченными обстоятельствами большинство задач, требующих
анализа установившихся режимов ЭЭС в процессе их проектирования, эксплуата-
ции или управления, решаются с помощью цифровой вычислительной техники
(ЭВМ, компьютеров). Ее основными достоинствами по сравнению с аналоговой
являются: большое удобство представления вводимой и выводимой информации;
большой объем решаемых задач; высокая скорость получения решения. В на-
стоящее время для решения многих задач, в том числе и для расчета установив-
шихся режимов, разработаны удовлетворительный математический аппарат и
программное обеспечение, позволяющие с помощью ЭВМ получать результаты
расчетов с заданной точностью и скоростью решения.
Процедура создания специализированного математического и сервисного
обеспечения решения задач с помощью ЭВМ включает в себя ряд этапов:
- постановку задачи (анализ исходных данных, математических закономер-
ностей их изменения и т.д.) и построение математической модели;
- разработку алгоритма решения задачи (алгоритмизацию);
- запись алгоритма на языке программирования;
- решение задачи с помощью ЭВМ;
- анализ полученных результатов.
Рассмотрим более подробно перечисленные этапы.
Постановка задачи – одна из самых квалифицированных и ответственных
частей решения задачи на ЭВМ. Она представляет собой определение независи-
мых и зависимых переменных в исследуемой задаче, определение математических
закономерностей, которые связывают эти переменные, границ изменения этих пе-
ременных и оценку возможных результатов.
Решение практической задачи начинается с описания исходных данных и
целей задачи на языке строго определенных математических понятий. Точная
формулировка условий и целей решения – это математическая постановка задачи.
Выделение наиболее существенных свойств реального объекта, описание их
с помощью математических соотношений – это этап построения математической
модели.
Построение математической модели является наиболее сложным и ответст-
венным этапом решения задачи. Она может иметь вид уравнения или системы
уравнений; может быть выражена в форме иных сколько угодно сложных матема-
тических структур или соотношений самой различной природы. Она может быть
непрерывной или дискретной, в зависимости от того, какими величинами она опи-
сана – непрерывными или дискретными. Однако, если выбранная математическая
модель слишком грубо отражает взаимосвязи изучаемого явления, то, какие бы
методы решения вслед за этим не применялись, найденные значения не будут от-
вечать условиям реальной задачи и окажутся бесполезными.
Таким образом, на этом этапе производится запись математических выра-
жений, описывающих каждое из явлений решаемой задачи, и создается единый
математический комплекс для всей задачи в целом в виде систем уравнений, в
12
общем случае, алгебраических, дифференциальных, интегральных и так далее с
привлечением методов дискретной математики или методов теории вероятностей.
В рамках построенной математической модели, осуществляется поиск мето-
да решения задачи и разрабатывается алгоритм ее решения. Этот этап называется
алгоритмизацией. Здесь используют любые формы представления алгоритма: сло-
весное описание, математические формулы, блок-схемы. В процессе записи алго-
ритма обязательно рассматриваются способ получения решения той задачи, кото-
рая ставится; возможность реализации выбранного метода решения в виде после-
довательного перечня операций, приводящих к решению; возможность получения
в ходе решения результатов с приемлемыми точностью и скоростью решения.
На следующем этапе алгоритм решения задачи записывают на языке про-
граммирования, позволяющем реализовать ее решение с помощью ЭВМ. В про-
стейшем случае может оказаться, что на этом этапе вовсе не составляется новая
программа для ЭВМ, а дело сводится, например, к использованию структурного
математического обеспечения ЭВМ. При записи новых сложных программ важное
место занимает процесс их отладки, проверки правильности реализации алгорит-
ма с помощью выбранного языка. При этом, чем больше выбранный язык адапти-
рован к характеру решаемой задачи и чем выше квалификация программиста, тем
быстрее идут процессы реализации алгоритма и окончательной отладки програм-
мы.
Эффективность решения задачи с помощью ЭВМ оценивается временем по-
лучения решения с заданной точностью и возможным объемом решаемой задачи.
Время решения зависит от степени соответствия математической модели описы-
ваемому явлению, от эффективности вычислительных методов, заложенных в ал-
горитм, наконец, от быстродействия самой вычислительной техники. Объем ре-
шаемой задачи определяется как особенностями применяемой математической
модели и алгоритма решения, так и оперативными характеристиками ЭВМ (на-
пример, объемом оперативной памяти).
Завершающий этап решения задачи – анализ результатов. Здесь происходит
осмысливание полученных результатов, сопоставление их с результатами кон-
трольного просчета, а также данными, полученными экспериментальным путем,
если таковые имеются. При этом одни результаты могут оказаться приемлемыми,
а другие – противоречащими смыслу реальной задачи. На этом этапе важно пра-
вильно оценить, соответствуют ли результаты физическому явлению, которое рас-
сматривается, и, если соответствуют, то какова их погрешность. Погрешность в
общем случае складывается из погрешности, вносимой неточностью задания ис-
ходных данных, погрешности математической модели, погрешности, заложенной
в алгоритме решения задачи и погрешности округления числовых величин ЭВМ
из-за ограниченного числа разрядов. При этом в некоторых случаях суммарная
погрешность может быть столь велика, что результаты расчетов могут быть не-
приемлемыми для использования.
Следует иметь в виду, что в некоторых случаях более точные математиче-
ские модели, учитывающие большее число факторов и более тонко отображаю-
щие физические зависимости рассматриваемых явлений, могут быть более чувст-
13
вительными к погрешностям исходных данных, чем более грубые. Поэтому важ-
но, чтобы выбираемый метод математического моделирования и метод численно-
го решения поставленной задачи были рассчитаны на введение таких данных, ко-
торые можно реально получить с нужной достоверностью. В противном случае,
целесообразно видоизменить метод получения количественных результатов, быть
может “загрубить” его и упростить с тем, чтобы затраты труда, связанные с при-
менением методов высокой точности, не оказались неоправданными.
1.3. Общие сведения о схемах замещения
Анализ режимов работы ЭЭС требует расчетов их параметров: напряжений
в узловых точках, токов и мощностей в элементах и др. Для выполнения таких
расчетов реальным ЭЭС обычно ставятся в соответствие так называемые схемы
замещения, представляющие собой совокупность схем замещения отдельных эле-
ментов ЭЭС, соединенных между собой в той же последовательности, что и в рас-
сматриваемых ЭЭС. По сути, схемы замещения – это электротехнические модели
ЭЭС, отражающие физическую сущность происходящих в них электрических и
магнитных процессов с помощью комплекса известных электротехнических эле-
ментов – источников напряжения, источников тока, сопротивлений, проводимо-
стей. На основании схем замещения ЭЭС создаются их математические модели,
которые реализуются, как правило, с использованием известных законов и мето-
дов электротехники: закона Ома, законов Кирхгофа, уравнений узловых потен-
циалов, уравнений контурных токов, метода наложения и др.
С целью облегчения расчетов режимов ЭЭС при составлении их схем заме-
щения и, соответственно, математических моделей могут вводиться некоторые
упрощающие допущения. Например, при составлении схем замещения ЭЭС для
расчета их рабочих установившихся режимов вводятся следующие допущения:
- считается, что трехфазные ЭЭС обладают циклической симметрией, т.е.
считается, что параметры пассивных их элементов (сопротивлений, проводимо-
стей) во всех трех фазах равны, а активных (ЭДС, источников токов) – равны по
величине и сдвинуты по фазе на 120°; при таких условиях трехфазные ЭЭС могут
рассматриваться на основании однофазных схем замещения, что в значительной
степени сокращает размерность решаемых задач;
- принимается, что параметры пассивных элементов ЭЭС являются посто-
янными по величине и не зависят от рассчитываемых параметров режима (напря-
жений, токов); это дает возможность считать, что коэффициенты при неизвестных
систем алгебраических уравнений, отражающих состояние ЭЭС, будут постоян-
ными и нелинейность уравнений может быть возможной только в связи с учетом
параметров активных элементов (ЭДС, источников тока), т.е. в связи с зависимо-
стью от параметров режима правых частей уравнений; в последнем случае реше-
ние уравнений осуществляется только с помощью применения итерационных ме-
тодов;
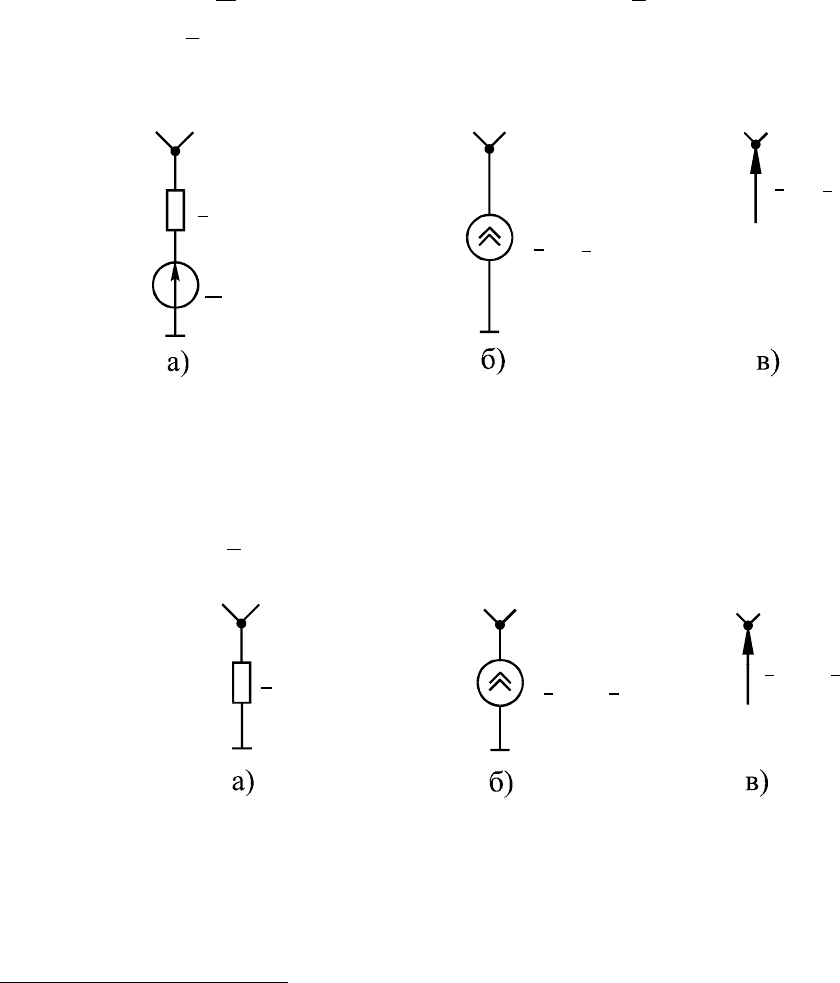
14
- считается, что в ЭЭС режимы токов и напряжений отвечают чисто сину-
соидальным законам изменения с частотой f = 50 Гц, т.е. какие-либо гармоники в
этих кривых отсутствуют; это также упрощает математическое описание рассчи-
тываемых процессов.
Важное место при составлении схем замещения занимает процедура исклю-
чения из схем трансформаторных связей – приведение схем замещения к одному
напряжению
*
. Эта процедура позволяет исключить из схем магнитные связи,
преобразовать их в чисто электрические цепи, что также в дальнейшем упрощает
создание математических моделей.
В расчетах параметров установившихся режимов источники электроэнергии
ЭЭС в схемах замещения могут быть представлены либо в виде источников на-
пряжения с ЭДС
Е и внутренним сопротивлением z (рис.1.3, а), либо в виде ис-
точников тока
у
I (рис.1.3, б). Последние чаще всего отображаются так называе-
мыми задающими токами (рис.1.3, в).
Рис.1.3
Нагрузки (потребители электроэнергии) имеют схемы замещения либо в ви-
де сопротивлений
z (рис.1.4, а), либо так же, как и источники питания, в виде ис-
точников тока и задающих токов (рис.1.4, б, в).
Рис.1.4
Величины токов источников тока и задающих токов, отображающих в схе-
мах замещения источники питания ЭЭС, принимаются равными значениям токов
*
Порядок расчета схем замещения и приведение их к одному напряжению рассмотрены в
разделе 6 данного пособия.
E
z
I
у
=
I
и.п.
I
у
=
I
и.п.
z
I
у
=
I
нг
_
нг
I
у
=
I
_

15
этих источников в предполагаемом установившемся режиме. Величины токов ис-
точников тока и задающих токов, отображающих нагрузки, принимаются с обрат-
ным знаком по отношению к токам нагрузки в предполагаемом режиме.
Линии электропередачи, трансформаторы подстанций и электростанций
представляются в схемах замещения ЭЭС в виде сопротивлений, причем схемы
замещения трансформаторов могут быть объединены со схемами замещения соот-
ветствующих источников питания, нагрузок и линий электропередачи.
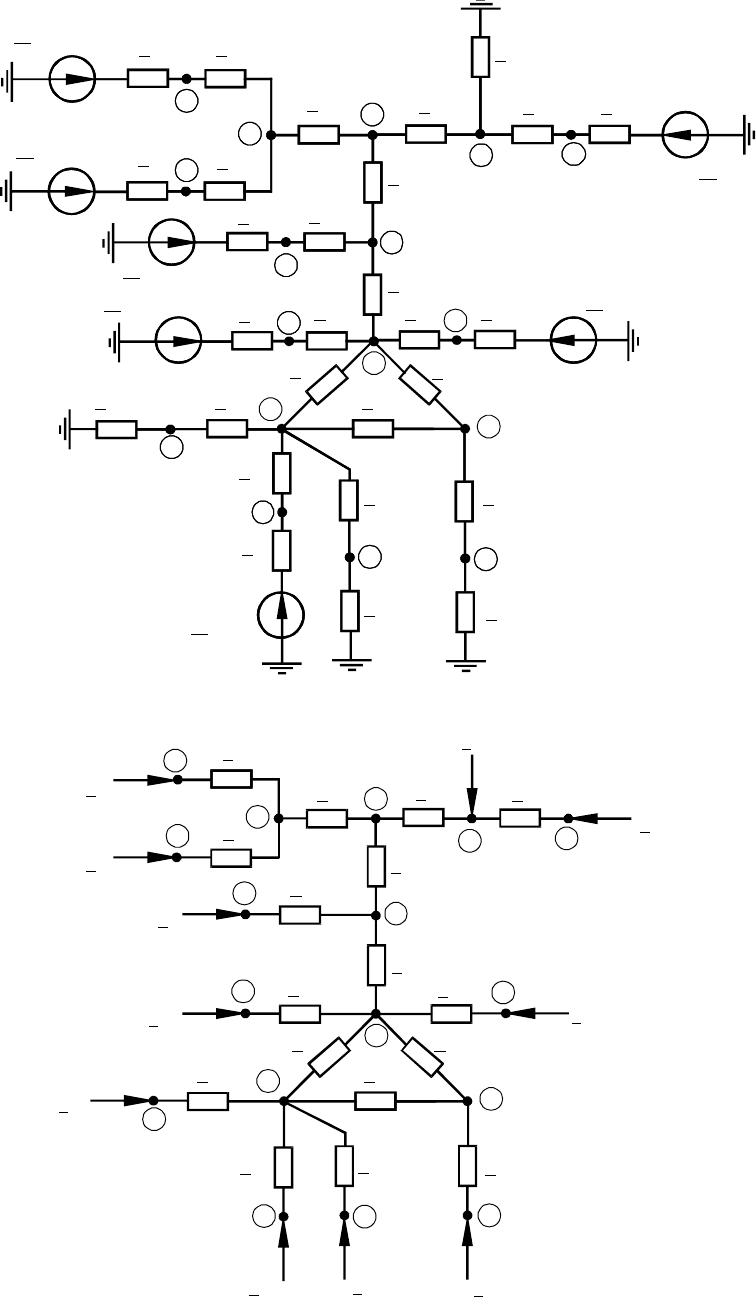
Один из вариантов схемы замещения электрической системы, изображенной
на рис.1.2, в котором электростанции представлены источниками напряжения, а
подстанции (трансформаторы и нагрузки) – сопротивлениями, показан на
рис.1.5,а. Другой вариант схемы замещения рассматриваемой системы, где как
электростанции, так и нагрузки подстанций представлены задающими токами, по-
казан на рис.1.5,б. Выбор того или иного варианта схемы замещения определяется
целями расчета, исходными данными и методикой расчета.
Поскольку схемы замещения ЭЭС, используемые для расчетов установив-
шихся режимов, представляют собой электрические цепи, то к ним применимы
такие понятия, характеризующие электрические цепи, как ветвь, узел и контур.
Как известно, ветвью называется участок цепи, который состоит из последова-
тельно соединенных ЭДС и сопротивления (либо только сопротивления), вдоль
которого в любой заданный момент времени ток имеет одно и то же значение.
Узел определяется как точка соединения двух или более ветвей, а контур – как
участок цепи, образованный таким последовательным соединением нескольких
ветвей, при котором начало первой ветви контура соединено с концом последней
в одном узле.
Схема замещения на рис.1.5,а содержит двадцать восемь ветвей и восемна-
дцать узлов: 1 – 17 и узел нейтрали (земли), имеющий нулевой потенциал. Ветви,
связанные с узлом нейтрали (ветви источников питания и нагрузок), называются
поперечными; остальные ветви – продольными.
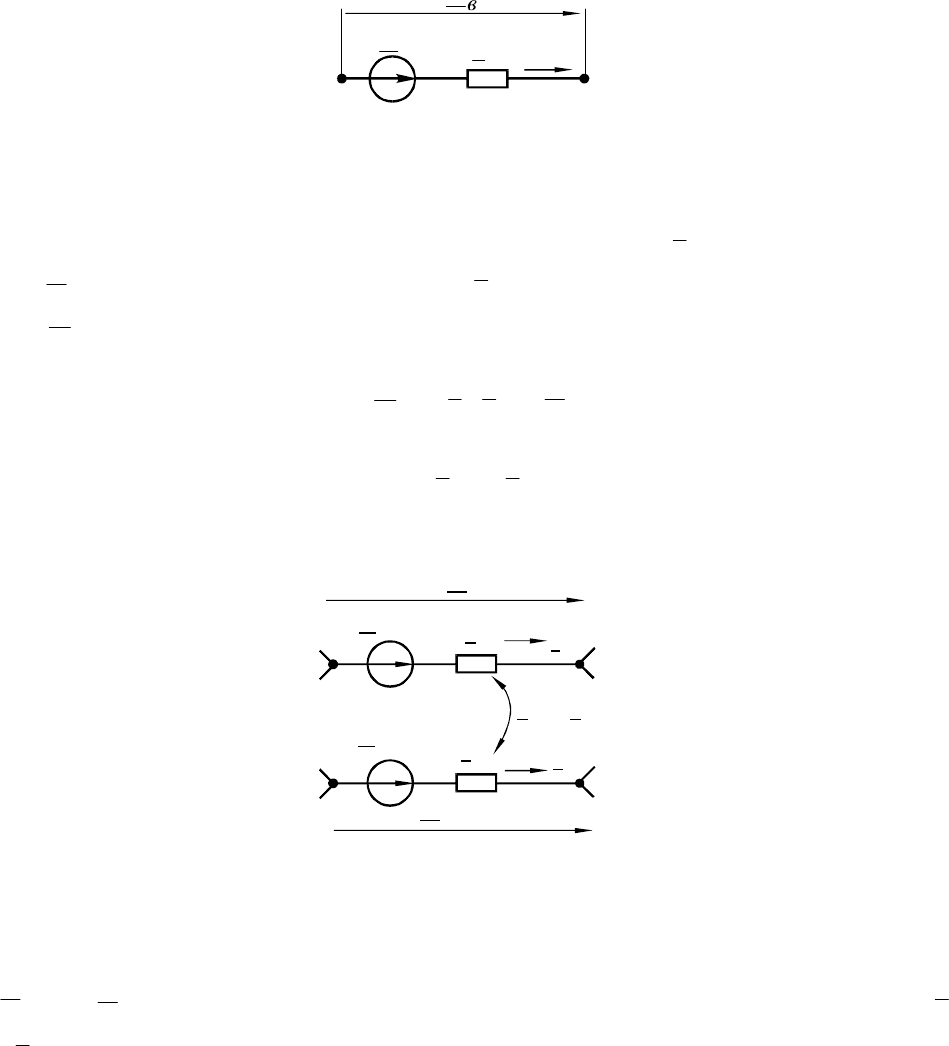
Схема замещения, показанная на рис.1.5,б, в которой источники питания и
нагрузки представлены задающими токами, содержит только семнадцать про-
дольных ветвей и семнадцать узлов, что определяется отсутствием узла нейтрали.
Обе рассматриваемые схемы содержат контуры, образуемые, например, линиями
5, 6, 8 (сопротивления
17
z ,
18
z ,
19
z ) и поэтому называются замкнутыми; при от-
сутствии контуров схема замещения называется разомкнутой.
16
Рис.1.5. Варианты схем замещения системы рис.1.2.
1
8
7
6
5
4
3
2
а)
E
ГЭС
E
ГЭС
E
ТЭЦ-5
E
ТЭЦ-3
z
7
z
8
z
НГ1
z
9
z
3
z
5
z
12
z
13
z
14
z
15
z
16
z
10
z
11
z
6
z
4
E
АЭС
E
СК
1
8
7
6
5
4
3
2
16
а)
E
ГЭС
E
ГЭС
E
ТЭЦ-5
E
ТЭЦ-3
z
1
z
1
z
2
z
2
z
7
z
8
z
НГ1
z
9
z
3
z
5
z
12
z
13
11
z
НГ4
z
20
E
E
ТЭЦ-4
z
21
z
22
12
ТЭЦ-4
z
21
z
22
13
z
НГ3
z
НГ3
z
23
z
23
15
z
НГ2
z
24
z
НГ2
z
24
z
14
z
15
z
16
z
10
z
11
z
6
z
4
E
АЭС
z
4
z
zz
6
z
7
z
9
z
11
z
10
z
14
z
15
z
20
z
22
z
23
z
24
I
ГЭС
I
ГЭС
I
СК
I
НГ1
I
АЭС
I
ТЭЦ-5
ТЭЦ-3
I
НГ4
ТЭЦ-4
I
НГ3
I
НГ2
1
2
3
4
5
6
7
8
16
17
11
z
17
z
18
z
19
9
10
14
z
17
z
18
z
19
9
10
14
12
13
б)
z
1
2
z
I
I
17
15
17
1.4. Система обозначений
Как известно, режим линейной электрической цепи, каковой и является схе-
ма замещения ЭЭС для расчета установившегося режима, полностью описывается
уравнениями законов Ома и Кирхгофа. Однако для записи этих уравнений долж-
ны быть приняты определенные обозначения. Остановимся кратко на используе-
мой далее системе обозначений.
Закон Ома устанавливает взаимосвязь параметров каждой из ветвей цепи.
Будем считать, что положительные направления параметров режима некоторой
той
-
i
ветви приняты от ее условного начала
n
к условному концу
к
(рис.1.6).
Рис.1.6 Положительные направления параметров режима ветви
Тогда для ветви, характеризующейся сопротивлением
вi
z , действующей в ней
ЭДС
вi
Е и протекающим по ней током
вi
I , разность потенциалов между ее кон-
цами
вi
U ( падение напряжения на ветви) в соответствии с законом Ома будет оп-
ределяться уравнением:
вiвiвi
вi
EIzU
-
=
(1.1)
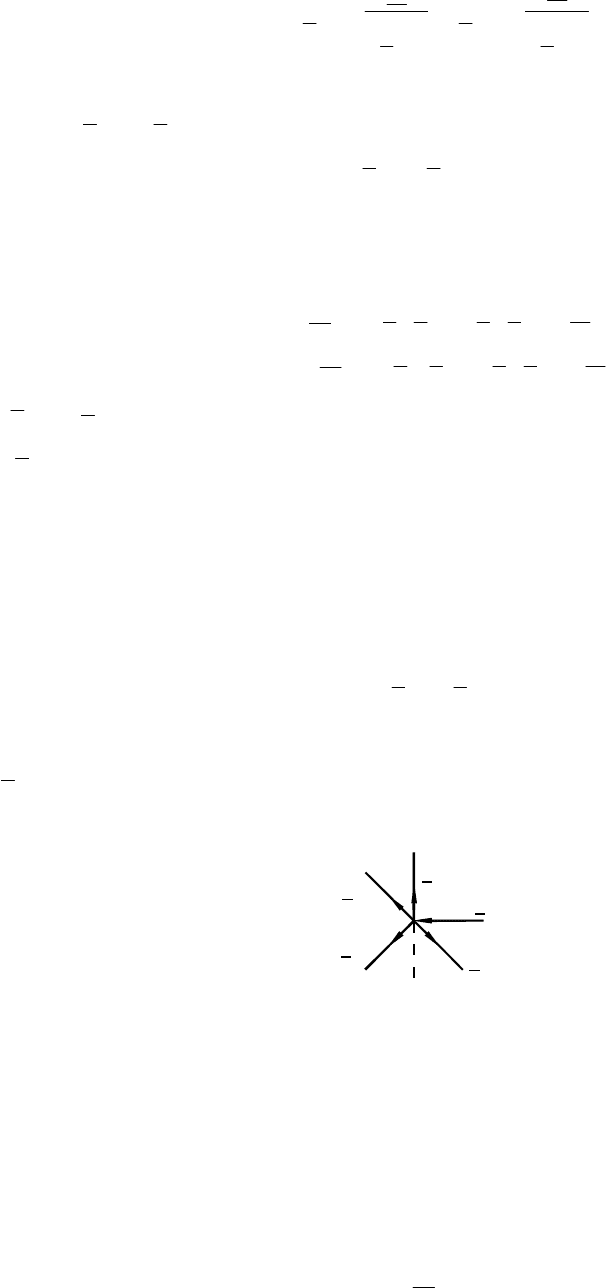
В общем случае между отдельными ветвями цепи
i
и
j
могут существо-
вать также взаимные сопротивления
ij
z и
ji
z , обусловленные, например, взаим-
ной индуктивностью (рис.1.7).
Рис.1.7 Ветви с взаимоиндуктивной связью.
Эти сопротивления характеризуют отношения величин ЭДС взаимоиндукции
вi
Е
D
и
вj
Е
D
, наведенных в ветвях
i
и
j
, к величинам наводящих их токов
вj
I
и
вi
I , протекающих соответственно в ветвях
j
и
i
:
n
к
в
I
i
в
z
i
в
E
i
U
i
в
Е
.
i
i
i
z
I
.
вi
U
вi
z
ij
=
z
ji
z
jj
I
.
вj
E
.
вj
U
вj
18
вj
вi
ij
I
E
z
D
= ;
вi
вj
ji
I
E
z
D
= .
В цепях, обладающих свойствами взаимности, величины взаимных сопро-
тивлений
ij
z и
ji
z не зависят от очередности записи индексов:
ij
z =
ji
z , (1.2)
поэтому, в предположении, что ЭДС самоиндукции и взаимоиндукции в ветвях
i
и
j
совпадают по направлению, связь между параметрами режимов ветвей
i
и
j
может быть определена следующими уравнениями:
вiвjijвiii
вi
EIzIzU
-
+
=
; (1.3)
вjвiijвjjj
вj
EIzIzU
-
+
=
; (1.4)
где
ii
z и
jj
z - собственные сопротивления ветвей;
ij
z - их взаимное сопротивление.
Первый закон Кирхгофа определяет баланс токов в каждом узле электри-
ческой цепи и формулируется следующим образом: алгебраическая сумма токов в
узле равна нулю. Принимая в качестве положительного направления для токов,
связанных с произвольным узлом, направление от узла (рис.1.8), уравнение перво-
го закона Кирхгофа получим в виде:
å
=
=-
s
i
увi
II
1
0, (1.5)
где
s
- число ветвей, связанных в узле;
у
I - источник тока, включенный в узел.
Рис.1.8 Положительные направления токов в узле.
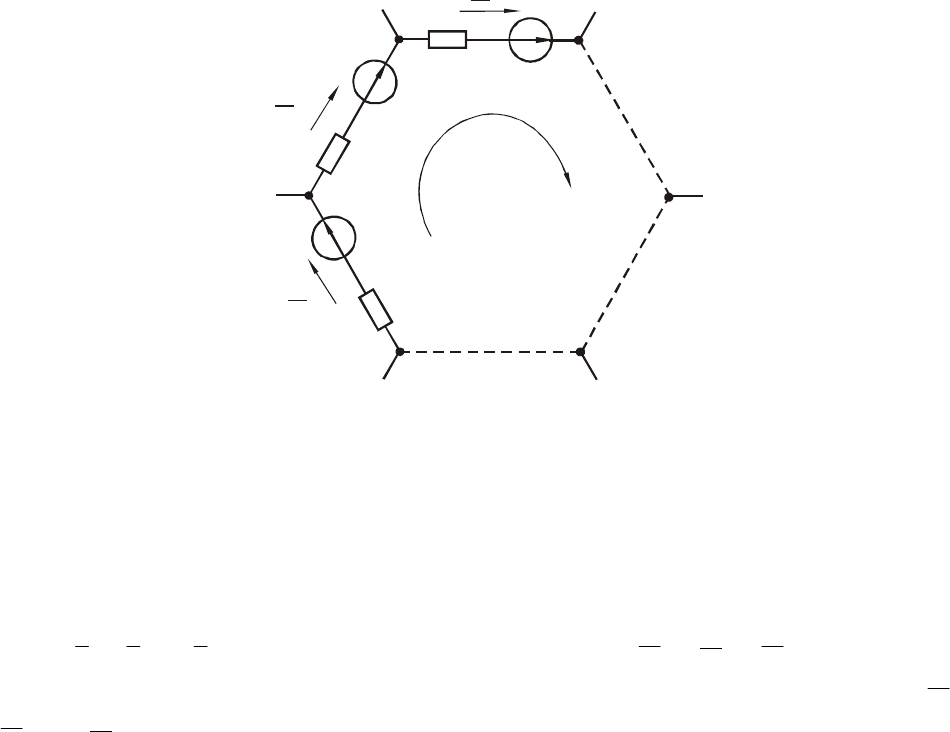
Второй закон Кирхгофа определяет баланс напряжений в замкнутых кон-
турах электрической цепи и формулируется следующим образом: алгебраическая
сумма падений напряжения на ветвях замкнутого контура равна нулю. Для произ-
вольного контура, содержащего
l
ветвей (рис.1.9), уравнение второго закона
Кирхгофа запишется в виде:
å
=
=
l
i
вi
U
1
0 . (1.6)
I
в
3
I
в
2
I
в
1
I
в
n
I
у
19
Обычно при составлении уравнений (1.6) падения напряжений ветвей, сов-
падающие с направлениям обхода контура учитываются в алгебраической сумме с
положительными знаками, а несовпадающие – с отрицательными.
Рис.1.9 Положительные направления напряжений в замкнутом контуре
Несмотря на то, что расчеты установившихся режимов работы трехфазных
ЭЭС чаще всего выполняются с помощью схем замещения, составленных для од-
ной фазы, характеристику этих режимов принято осуществлять с помощью пара-
метров режимов, свойственных трехфазным системам: комплексными величинами
токов
А
I ,
В
I и
С
I (рис.1.10), фазных напряжений -
А
U ,
В
U ,
С
U , определенных
относительно нейтрали или земли, междуфазных (линейных) напряжений -
АВ
U ,
ВС
U и
СА
U .
Чаще всего однофазные схемы замещения составляются и рассчитываются
для фазы А ЭЭС (рис.1.10, б), т. к. для трехфазной системы, обладающей цикли-
ческой симметрией, при известных комплексах параметров режима фазы А пара-
метры фаз В и С легко определяются с помощью коррекции фазовых углов векто-
ров, отвечающих фазе А (рис.1.10, в).
U
в
1
U
2
в
U
в
3
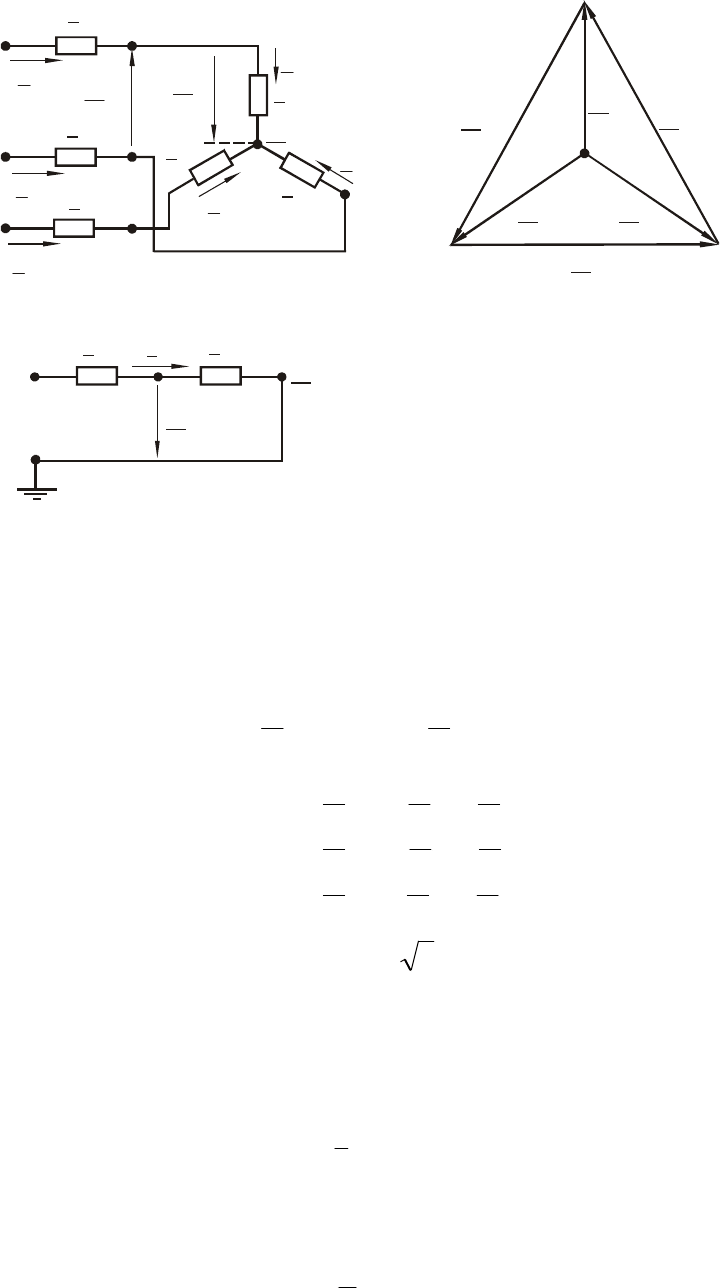
20
Рис.1.10 Пояснение к системе обозначения параметров режима трехфазной
системы: а, б – трехфазная и однофазная схемы замещения; в – векторная диа-
грамма напряжений трехфазной симметричной системы.
Векторы междуфазных
U и фазных
ф
U напряжений трехфазной системы
связаны соотношениями (рис.1.10, в):
;UUU
;UUU
;UUU
АССА
СВВС
ВААВ
-=
-=
-
=
а для модулей этих величин получим:
ф
UU 3= (1.7)
Напомним, что номинальные напряжения электрических сетей – это между-
фазные напряжения.
Комплексные сопротивления элементов схем замещения ЭЭС будем пред-
ставлять в виде суммы активной
r
и реактивной
x
их составляющих:
вi
вi
вi
jxrz
+
=
, (1.8)
где
x
- применяется со знаком плюс для индуктивных элементов и со знаком ми-
нус – для емкостных.
Проводимости элементов будем представлять как:
jвgY
-
=
, (1.9)
где
в
также применяется со знаком плюс для индуктивных элементов и со знаком
минус – для емкостных.
z
z
U
A
H
N
U
= 0
a)
U
фА
U
U
U
AB
BС
CA
U
фВ
U
фС
в)
z
z
z
H
I
A
U
A
U
N
=0
б)
Л
Л
Л
Л
H
z
z
H
z
I
I
А
А
U
АВ
I
I
I
I
В
В
С
С
