Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей

Подождите немного. Документ загружается.

3. МАТРИЧНАЯ ЗАПИСЬ УРАВНЕНИЙ СОСТОЯНИЯ

ЭЛЕКТРИЧЕСКОЙ СЕТИ

3.1. Обобщенное уравнение состояния

Матрицы

дают возможность записать уравнение состояния электри-

ческой цепи в матричной форме.

Система взаимно независимых уравнений первого и второго законов Кирх-

гофа может быть представлена в виде (2.24) и (2.34):

ув

M ,

UN ,

Чтобы ввести в уравнения второго закона Кирхгофа токи в ветвях схемы,

воспользуемся законом Ома в матричном виде:

EZU

I , (3.1)

где

Z квадратная диагональная (при отсутствии взаимных сопротивлений) мат-

рица сопротивлений ветвей:

KKKK

;

E матрица-столбец ЭДС ветвей;

I матрица-столбец токов ветвей.

Умножив выражение для

U на матрицу

слева, получим:

ENZNUN

I . (3.2)

где

кв

EEN

- матрица-столбец контурных ЭДС, представляющий собой алгеб-

раические суммы ЭДС ветвей, входящих в каждый независимый контур. После

преобразования (3.2) можно записать:

квв

ув

EZN

=××

(3.3)

Эти уравнения можно объединить в одно, если матрицы

рассмат-

ривать как блоки одной объединенной матрицы параметров схемы замещения сис-

темы:

А ,

а матрицы

I и

E рассматривать как блоки одной объединенной матрицы исход-

ных параметров режима:

Тогда обобщенное уравнение состояния примет вид:

=×

EZN

M I

I . (3.4)

Здесь матрица

является квадратной и в обычных условиях неособенной,

т.е. для нее может быть найдена обратная матрица

, после чего можно опреде-

лить все параметры режима.

Если схема электрической сети не содержит замкнутых контуров, (чаще все-

го это бывает в распределительных сетях, где не осуществляется параллельное ре-

зервирование, а питание потребителей в рабочем режиме происходит по одной це-

пи), то для такой схемы нет необходимости составлять уравнения по второму за-

кону Кирхгофа, поскольку отсутствуют замкнутые контуры. В этом случае уравне-

ние приобретает более простой вид:

ув

Поскольку в разомкнутой схеме отсутствуют замкнутые контуры, матрица

одновременно является матрицей дерева

М , т.е. квадратной и неособенной. Сле-

довательно, для нее может быть получена обратная матрица, и уравнение может

быть разрешено относительно токов ветвей:

ув

II ×=

Введем обозначение

СM =

где

С матрица коэффициентов распределения.

Тогда обобщенное уравнение состояния для разомкнутой сети можно записать в виде:

урв

С . (3.5)

Для разомкнутых схем матрица

С может быть получена непосредственно

путем исследования топологии графа сети. Число столбцов матрицы

С равно

числу узлов схемы без балансного, а число строк равно числу ветвей.

Матрица

С составляется по столбцам. В каждом столбце прослеживается

путь графа от каждого узла к балансному узлу. Если ветвь входит в состав данного

пути с тем же направлением, то в матрицу

C вносится “+1”; если не совпадает,

то “-1”, если ветвь не входит в путь – “0”.

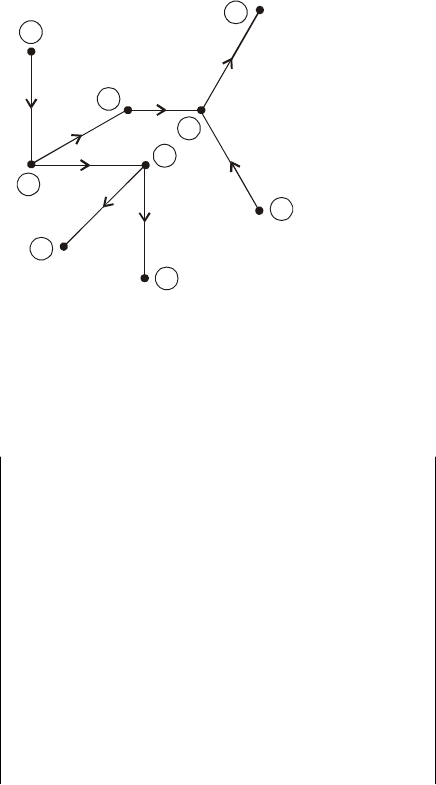
Рис. 3.1. К составлению матрицы коэффициентов распределения

Например, для схемы, изображенной на рис.3.1, считая узел 9 балансным,

матрицу

С получим в виде:

---

----

01000000

11100000

00100000

00010000

00000100

00011100

00011101

11111111

Следует отметить, что при использовании обобщенного уравнения состоя-

ния количество решаемых уравнений получается наибольшим, поскольку неиз-

вестными являются токи ветвей. Кроме того, для составления матрицы

необхо-

димо в схеме выделять независимые контуры, а эта операция неоднозначна. Дос-

таточно трудоемким является алгоритм расчета остальных параметров режима.

3.2. Уравнение узловых напряжений

Уравнений узловых напряжений в матричной форме выводятся на основании

закона Ома (3.1) и уравнения (2.31), связывающего напряжения ветвей с напряже-

ниями узлов относительно балансного узла:

EZU

I ;

UMU

Приравняем правые части уравнений:

EZUM

I .

Решим уравнения относительно токов ветвей:

(

)

EUMZ +=

-1

I ,

Используя матричную форму записи первого закона Кирхгофа, получим:

(

)

увtв

I=+×

][ EUMZM

Перенесем известные в правую часть:

ввуtв

ЕМZUМMZ

-= I

Введем обозначение:

tвtву

MMYMMZY ==

где

Y матрица узловых проводимостей,

YZ =

матрица проводимостей ветвей.

Тогда окончательную форму записи системы узловых уравнений получим в виде:

ввуу

ЕMYUY

I (3.6)

Эти уравнения записаны для напряжений относительно балансного узла.

Матрица

Y является квадратной и неособенной, следовательно, имеет об-

ратную.

Проанализируем структуру матричной формы записи уравнений узловых на-

пряжений.

Диагональные элементы матрицы

Y представляют собой собственные про-

водимости узлов:

jii

где

- число ветвей, подключенных к узлу.

Иными словами, собственная проводимость узла равна сумме проводимо-

стей ветвей, присоединенных к данному узлу.

Недиагональные элементы матрицы

Y (взаимные проводимости) равны

взятым с обратным знаком проводимостям ветвей, включенных между узлами

jiк

Если между узлами i и к отсутствует непосредственная связь, то 0

iк

Y .

Если в схеме отсутствуют источники напряжения, то уравнение узловых на-

пряжений принимает более простой вид:

уу

UY (3.7)

Так как

Y - квадратная и неособенная, то имеет обратную

Y . Следовательно,

уравнение может быть разрешено относительно напряжений

U :

уу

= YU .

Среди особенностей уравнений узловых напряжений можно выделить сле-

дующие:

- число этих уравнений для сложных схем примерно в 1,5 раза меньше, чем

при составлении обобщенных уравнений состояния;

- матрица узловых проводимостей

Y симметрична относительно главной

диагонали и содержит большое количество нулевых элементов; оба эти обстоя-

тельства позволяют повысить эффективность решения систем уравнений;

- диагональные элементы матрицы

Y обычно превышают по абсолютной

величине недиагональные элементы, что способствует повышению точности вы-

числений при использовании численных методов;

- так как матрица

Y является квадратной и неособенной, то для нее может

быть найдена обратная матрица

Y , что можно использовать для многократного

решения системы уравнений при итерационных способах;

- матричная форма записи уравнений узловых напряжений имеет опреде-

ленные преимущества по сравнению с аналитической формой записи, т.к. позволя-

ет учесть не только собственные сопротивления ветвей, но и взаимные (отражаю-

щие взаимоиндукцию между ветвями). Механизм учета заложен в использовании

общей формы матрицы

Z , в диагонали которой находятся собственные сопро-

тивления ветвей, а недиагональными элементами могут быть взаимные сопротив-

ления; при формальном обращении матрицы

Z автоматически учитываются вза-

имные сопротивления, что может способствовать линеаризации решения некото-

рых уравнений.

3.3. Уравнение контурных токов

Как и в аналитической форме, уравнения контурных токов в матричной

форме выводятся на основании уравнений второго закона Кирхгофа, записанных

для замкнутых контуров. Их использование также позволяет снизить порядок сис-

темы решаемых уравнений по сравнению с использованием системы обобщенных

уравнений состояния.

Как было показано выше, удобно пользоваться системой базисных конту-

ров. Будем считать, что независимые контуры выбраны как базисные, и запишем

для этого случая уравнение второго закона Кирхгофа:

Учитывая, что

вввв

I и

квв

получим

ENZ

I .

Подставив выражение (2.51) в записанное уравнение, получим:

квtвув

ЕNNZ

NZ =+×

. (3.8)

Учитывая, что

вк

, где

I матрица-столбец контурных токов, можно

записать:

увккtв

II ×

NZENNZ . (3.9)

Введя обозначение

ZNNZ

, где

Z квадратная неособенная матрица

контурных сопротивлений, получим окончательно:

увккк

II ×

NZEZ . (3.10)

Таким образом, выражения (3.9) и (3.10) отвечают матричной форме записи

уравнений контурных токов.

Если в схеме отсутствуют источники токов, то уравнение приобретает более

простой вид:

I . (3.11)

Матрица

Z представляет собой симметричную матрицу, в диагонали кото-

рой расположены собственные сопротивления контуров, определяемые суммиро-

ванием сопротивлений ветвей, входящих в данный контур, а недиагональные эле-

менты представляют собой взаимные сопротивления контуров (сопротивления, по

которым контурные токи протекают совместно), входящие в матрицу со знаком

“+”, если контурные токи при обтекании рассматриваемой взаимной ветви имеют

одинаковые направления и со знаком “-”, если контурные токи имеют разное на-

правление в пределах данной ветви.

Так как

Z - симметрична и в общем случае является разряженной, то для

нее справедливы те же самые положения, что и для матрицы

Y , т.е. возможность

компактного хранения в ЭВМ и повышение эффективности решения уравнений.

Как видно из сопоставления двух форм записи уравнений, с учетом токов

узлов и без учета токов узлов, наиболее рационально использование уравнений

контурных токов, когда в схеме отсутствуют задающие токи, т.к. в противном

случае приходится формировать матрицу дерева и обращать ее.

Тем не менее, это только внешний факт упрощения, т.к. для сложной схемы,

чтобы получить

Z , необходимо применить алгоритм формализованного получе-

ния матрицы

, а эта операция также связана с необходимостью выделения ба-

зисных контуров путем выделения дерева и хорд схемы.

Таким образом, уравнение контурных токов обладает тем же самым недос-

татком, что и обобщенное уравнение состояния, хотя порядок системы уравнений

в этом случае оказывается значительно меньше.

Так как,

Z - квадратная и неособенная матрица, то для нее может быть

найдена обратная, и решение уравнения может быть записано в виде:

=I ,

что в случае решения нелинейных задач может быть использовано для рациональ-

ного построения итерационных процессов.

3.4. Обобщенные параметры схем электрических систем

Преобразования уравнений состояния сложных схем показывают, что наря-

ду с “натуральными” параметрами, собственными и взаимными сопротивлениями

ветвей, которые входят в матрицу сопротивлений ветвей

Z , часто применяют

обобщенные параметры.

Обобщенные параметры входят, например, в следующие матрицы: узловых

проводимостей

Y , узловых сопротивлений

Z , контурных проводимостей

Y ,

коэффициентов распределения задающих токов

С и т.д.

Эти матрицы характеризуют свойства схемы в целом, не отражая отдельных

параметров схемы. Следовательно, по обобщенным параметрам нельзя восстано-

вить схему, так как одним и тем же обобщенным параметрам могут соответство-

вать разные схемы. Обобщенными параметрами могут быть не только пассивные,

но и активные параметры, например, контурные э.д.с.

Е .

Если рассмотреть обобщенное уравнение состояния (3.4), уравнение узло-

вых напряжений (3.6) и уравнение контурных токов (3.10), то, разрешая их отно-

сительно неизвестных, нетрудно получить следующие выражения:

вЕуIв

ENВВ

II , (3.12)

где

[ ]

ЕI

ВВВ ;

ввууу

ЕYМZZU

I ; (3.13)

вкувкк

ЕNY

NZY

×+

-= I

I (3.14)

Сравнивая выражения (3.12), (3.13), (3.14) можно отметить, что при опреде-

лении токов ветвей, напряжений узлов и токов контуров в общем случае уравне-

ния состоят из двух частей: первая часть определяет влияние токов в узлах на ре-

жим сети, вторая – влияние источников э.д.с. ветвей.

При линейности схемы каждая из этих задач может решаться отдельно, а ре-

зультат можно найти суммированием полученных решений в каждой из задач. В

этом состоит суть метода наложения.

Константы, связывающие в каждом из уравнений (3.12) – (3.14) вынуждаю-

щие силы (

I ,

Е ) с неизвестными параметрами режима (

I ,

U ,

I ), также как и

Z и

Y являются обобщенными характеристиками схемы электрической сети.

4. МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ СОСТОЯНИЯ

ЭЛЕКТРИЧЕСКОЙ СЕТИ

4.1. Линейные и нелинейные уравнения состояния

Основной задачей расчета режимов работы электрических систем и сетей

(нормальных, аварийных, послеаварийных) является определение мощностей, то-

ков, напряжений (а также их углов). При этом в математическом плане можно вы-

делить два тип задач:

- линейные задачи, в которых все коэффициенты систем уравнений, свя-

занные с характеристикой пассивных элементов сети (сопротивления, проводимо-

сти), и связанные с характеристиками вынуждающих сил (источники токов, ЭДС)

имеют постоянную величину. Для решения таких задач применяются методы ре-

шения систем линейных алгебраических уравнений.

- нелинейные задачи, связанные с решением нелинейных систем уравнений.

Нелинейность систем уравнений может быть обусловлена нелинейностью пассив-

ных элементов сети, например, зависимостью индуктивных сопротивлений от на-

пряжения, или нелинейностью вынуждающих сил; например, зависимостью ис-

точников токов в узлах, отражающих действие нагрузок и генераторов в схеме, от

напряжения узлов. На современном уровне развития математики решение таких

задач требует привлечения итерационных способов, например, метода Ньютона,

метода внешней итерации и т.д.

Обычно при решении задач расчета установившихся режимов работы элек-

трических систем нелинейностью пассивных элементов пренебрегают, полагая,

что в диапазоне рассчитываемых величин напряжений они остаются неизменны-

ми.

Таким образом, основная нелинейность системы уравнений может быть свя-

зана с нелинейностью вынуждающих сил.

4.2. Особенности систем линейных уравнений и методы их решения

Линейные алгебраические уравнения, используемые для расчета устано-

вившихся режимов электрических систем, имеют следующие особенности:

- в большинстве случаев матрица коэффициентов системы уравнений явля-

ется слабо заполненной, т.е. имеет большое количество нулевых элементов; на-

пример, число ненулевых элементов в матрице узловых проводимостей для слож-

ных схем с большим количеством узлов составляет примерно 4n, т.е. n

– 4n эле-

ментов этой матрицы равны нулю, поскольку не все узлы имеют непосредствен-

ную связь между собой;

- диагональные элементы матрицы коэффициентов не равны нулю и обыч-

но по абсолютной величине превосходят недиагональные элементы соответст-

вующей строки и столбца; это способствует повышению сходимости при исполь-

зовании итерационных процессов;

- при использовании уравнений узловых напряжений и уравнений контур-

ных токов матрица коэффициентов системы симметрична относительно главной

диагонали.

Учет этих особенностей при реализации вычислительных методов позволяет

значительно повысить эффективность процесса получения решения за счет ис-

ключения операций с нулевыми элементами и уменьшения требуемой оператив-

ной памяти ЭВМ и времени расчета.

Важным моментом, определяющим возможность решения линейной систе-

мы уравнений и достоверность этого решения, является хорошая обусловленность

матрицы ее коэффициентов. Если матрица коэффициентов плохо обусловлена

(т.е. определитель этой матрицы стремится к нулю), то система может иметь бес-

конечное множество решений или может иметь решения, не отвечающие физиче-

ской сути задачи, а в некоторых случаях при применении итерационных методов

может вообще не давать решений (процесс итерации не сходится). Обычно такая

ситуация возникает, когда при составлении уравнений либо имеют место большие

погрешности в задании исходной информации, либо имеют место ошибки в со-

ставлении математической модели процесса, либо система уравнений не отвечает

физике рассматриваемого явления.

В дальнейшем будем полагать, что во всех рассматриваемых нами задачах

системы уравнений состояния для нормального режима работы сети имеют хоро-

шо обусловленную матрицу коэффициентов, и для них могут быть применены

традиционные численные методы решения и могут быть получены обратные мат-

рицы.

Современные методы решения систем алгебраических уравнений можно

разделить на две группы:

- прямые (точные) методы (дают решение системы за конечное число ариф-

метических операций);

- итерационные (приближенные) методы.

Среди точных методов также можно выделить две группы:

- к первой группе относятся метод Гаусса с обратным ходом, метод Гаусса

без обратного хода (метод Жордана - Гаусса) и их модификации; по сути эти ме-

тоды реализуют известный принцип исключения переменных;

- ко второй группе относятся методы, использующие для решения системы

уравнений обратные матрицы коэффициентов. Наиболее часто они применяются,

когда обратная матрица используется многократно, или когда обратная матрица

может быть получена на основании анализа топологии сети без трудоемкой опе-

рации обращения.

Итерационные методы дают решение системы как предел последовательных

приближений к точному решению, которое задается коэффициентом точности,

определяющим разность между точным решением и его приближенным значени-

ем, удовлетворяющим расчетчиков. Таким образом, итерационным способом

нельзя получить точное решение, а только приближенное с заданной степенью

точности. К итерационным методам относится метод простой итерации, метод

Зейделя, градиентные методы.

4.3. Решение уравнений состояния методом Гаусса

В основе практически всех прямых методов решения линейных систем ал-

гебраических уравнений установившихся режимов электрических систем лежит

метод Гаусса или его модификации.

4.3.1. Метод Гаусса с обратным ходом

Это наиболее рациональный и распространенный метод решения систем

уравнений произвольного порядка, реализующий последовательное исключение

переменных и затем последующую подстановку для получения решений.

Решение системы

алгебраических уравнений вида

по данному алгоритму состоит из двух этапов. На первом этапе в результате пре-

образований, заключающихся в исключении всех неизвестных, расположенных

ниже главной диагонали, матрица коэффициентов А превращается в верхнюю

треугольную, а последнее уравнение оказывается разрешенным относительно не-

известного. На втором этапе определяются все неизвестные системы уравнений.

Рассмотрим применение метода Гаусса на примере системы из трех уравне-

ний:

3333232131

2323222121

1313212111

bxaxaxa

=++

(4.1)

При исключении по методу Гаусса применяется стандартная операция, ко-

торая позволяет упорядочить исключение и получить удобный алгоритм для реа-

лизации этого метода на ЭВМ.

Решение состоит в том, что на каждом шаге преобразования системы (число

шагов равно

(

)

n , где

порядок решаемой системы) исключается одна из пе-

ременных из всех нижестоящих уравнений системы. Особенностью метода явля-

ется то, что для проведения операции исключения на каждом шаге используется

главный диагональный элемент, каковым является коэффициент при исключае-

мом неизвестном в главном уравнении, т.е. в уравнении, в котором это неизвест-

ное остается.

Так как главный диагональный элемент входит в коэффициент преобразова-

ния в знаменателе, то обязательным условием возможности применения этого ме-

тода является неравенство нулю главного диагонального элемента на каждом ша-

ге преобразований. Если все же он оказался равным нулю, то перед выполнением