Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей
Подождите немного. Документ загружается.


61
очередного шага уравнения преобразуемой системы должны быть так переставле-
ны, чтобы главный диагональный элемент не оказался нулевым.
Первый шаг. Будем считать, что 0
11
¹
a . Запишем коэффициенты преобра-
зования для каждого уравнения. Первое уравнение является главным, из второго и
третьего исключается неизвестное
1
x .
() ()
11
31
1
3
11
21
1
2
a
a
m;
a
a
m == .
Чтобы исключить из второго уравнения неизвестное
1
x , умножим первое уравне-
ние на коэффициент
(
)
1
2
m и вычтем результат из второго уравнения:
(
)
(
)
()
(
)
()
(
)
()
4434421
444344421444344421444344421
1
2
1
1
223
1
23
13
1
2232
1
22
12
1
2221
0
11
1
221
b
bmbx
a
amax
a
amaxama ×-=
÷
ø
ö
ç
è
æ
×-+
÷
ø
ö
ç
è
æ
×-+
÷
ø
ö
ç
è
æ
×-
Для исключения неизвестного
1
x из третьего уравнения умножим первое
уравнение на коэффициент
(
)
1
3
m и результат умножения вычтем из третьего урав-
нения:
(
)
(
)
(
)
(
)
()
(
)
(
)
()
(
)
()
43421443442144344214434421
1
3
1
1
3
33
1
33
13
1
3
332
1
32
12
1
3
321
0
11
1
3
31
b
bmbx
a
amax
a
amaxama ×-=×-+×-+×-
Таким образом, исходная система уравнений преобразуется к виду:
() () ()
() () ()
1
3
3
1
33
2
1
32
1
1
2
3
1
23
2
1
22
1
1313212111
0
0
bxaxax
bxaxax
bxaxaxa
=++×
=++×
=
+
+
(4.2)
Второй шаг. Аналогичные преобразования производятся при условии, что
главным уравнением является второе уравнение, так как будет исключаться вто-
рое неизвестное из уравнения ниже второго. Главным элементом будет считаться
элемент
(
)
1
22
a . Операция производится совершенно аналогично первому шагу. По-
скольку рассматривается система из трех уравнений, то преобразованию подвер-
гается только третье уравнение.
Определим коэффициент преобразования для третьего уравнения:
()
(
)
()
1
22
1
32
2
3
a
a
m = .
Умножим коэффициент
(
)
2
3
m на второе уравнение и результат умножения
вычтем из третьего уравнения:
(
)
(
)
(
)
(
)
(
)
()
(
)
(
)
(
)
()
443442144344214434421
2
3
1
2
2
3
1
3
3
2
33
23
2
3
1
33
2
0
1
22
)2(
3
)1(
32
1
0
b
bmbx
a
amaxamax ×-=×-+×-+× .
В результате получим:

62
() () ()
() ()
2
3
3
2
33
21
1
2
3
1
23
2
1
22
1
1313212111
00
0
bxaxx
bxaxax
bxaxaxa
=+×+×
=++×
=
+
+
(4.3)
На этом заканчивается первый этап решения (прямой ход), так как все ко-
эффициенты ниже главной диагонали нулевые.
Обратный ход (второй этап, процесс подстановки):
(
)
()
() ()
()
() ()
( )
.
1
1
3132121
11
1
1
22
2
33
2
3
1
23
1
22
2
33
2
3
3
xaxab
a
x
aa
b
abx
a
b
x
×-×-=
×
÷
÷
ø
ö
ç
ç
è
æ
×-=
=
Для данного метода может быть использована модификация – преобразуют-
ся не только ниже стоящие уравнения по отношению к главному, но и само глав-
ное уравнение. В этом случае главный диагональный элемент превращается в
единицу.
Рассмотренная последовательность выполнения операций достаточно легко
реализуется с помощью ЭВМ.
4.3.2. Метод Гаусса без обратного хода (метод Жордана)
В отличие от метода Гаусса с обратным ходом, метод Гаусса без обратного
хода в процессе реализации прямого хода решения разрешает систему относи-
тельно неизвестных, то есть уже к концу прямого хода фактически получается
решение системы уравнений, и нет необходимости в обратной подстановке. Реа-
лизация этого метода совершенно аналогична методу Гаусса с обратным ходом.
Отличие состоит лишь в том, что операции по исключению неизвестных ведутся
не только с элементами, стоящими ниже диагонали, но и с элементами, стоящими
выше диагонали.
Как и в методе Гаусса с обратным ходом, необходимым условием является
неравенство нулю главного диагонального элемента.
Рассмотрим данный метод на примере решения системы из трех уравнений
(4.1):
.
3333232131
2323222121
1313212111
bxaxaxa
bxaxaxa
bxaxaxa
=++
=++
=
+
+
Первый шаг. Определим коэффициенты преобразований для второго и
третьего уравнений:

63
()
()
.
,
11
31
1
3
11
21
1
2
a
a
m
a
a
m
=
=
Умножая поочередно первое уравнение на коэффициенты
(
)
(
)
1
3
1
2
и mm и вы-
читая результат соответственно из второго и третьего уравнений, получим:
() () ()
() () ()
.0
0
1
3
1
3332
1
321
1
23
1
232
1
221
1313212111
bxaxax
bxaxax
bxaxaxa
=++
=++
=
+
+
Второй шаг. Для исключения неизвестного
2
х из первого и третьего урав-
нений определим соответствующие коэффициенты преобразований:
()
()
()
()
()
.
,
1
22
1
32
2
2
1
22
12
2
1
a
a
m
a
a
m
=
=
Умножая второе уравнение поочередно на
(
)
2
1
m и
(
)
2
3
m и вычитая результат
умножения соответственно из первого и третьего уравнений, получим:
(
)
(
)
() () ()
() ()
.00
0
0
2
3
3
2
3321
1
23
1
232
1
221
2
13
2
132111
bxaxx
bxaxax
bxaxxa
=++
=++
=++
(4.4)
Третий шаг. Определим коэффициенты преобразований для первого и вто-
рого уравнений:
()
(
)
()
()
()
()
.
,
2
33
1
23
3
2
1
22
2
13
3
1
a
a
m
a
a
m
=
=
В результате произведения операций, аналогичных выполненным на первом
и втором шагах, получим:
(
)
() ()
() ()
.00
00
00
2
33
2
3321
3
232
1
221
3
132111
bxaxx
bxxax
bxxxa
=++
=++
=++
(4.5)
Тогда:

64
(
)
11
3
1
1
a
b
x = ;
(
)
()
1
22
3
2
2
a
b
x = ;
(
)
()
2
33
2
3
3
a
b
x =
.
Достоинства методов Гаусса состоят в том, что они гарантированно дают
решение в результате выполнения определенного числа несложных арифметиче-
ских операций, которое определяется только порядком решаемой системы урав-
нений. Кроме того, метод позволяет учесть симметрию матрицы коэффициентов и
наличие в ней нулевых элементов.
Недостатки методов Гаусса связаны с необходимостью запоминания матри-
цы коэффициентов системы уравнений и необходимостью проверки на неравенст-
во нулю на каждом шаге главного диагонального элемента.
4.3.3. Сравнительная вычислительная эффективность методов Гаусса с об-
ратным ходом и без обратного хода
Вычислительная эффективность метода оценивается на основании следую-
щих показателей:
- общее число операций умножения и деления, которое необходимо выпол-
нить при реализации метода для решения в общем случае системы уравнений по-
рядка
n
; операции умножения и деления принимаются в качестве оценочных, так
как они состоят из элементарных операций сложения и вычитания и являются
наиболее длительными по времени выполнения;
- возможность экономного использования памяти ЭВМ, так как от этого за-
висит объем решаемых задач (порядок решаемых систем уравнений);
- возможность получения точного решения при наличии округлений, возни-
кающих из-за конечного числа разрядов в современных ЭВМ, т.е. из-за необходи-
мости так или иначе отбрасывать часть информации о числах, не помещающихся
в разрядную сетку.
Общее количество операций умножения и деления может быть подсчитано
по следующим выражениям:
- для метода Гаусса с обратным ходом
(
)
3
13
2
1
-+
=
nnn
К ;
- для метода Гаусса без обратного хода
(
)
2
1
2
2
+
=
nn
К ,
где
-
n
число уравнений.
В табл. 4.1 представлены расчеты по приведенным выражениям в зависимо-
сти от порядка решаемой системы уравнений.

65
Таблица 4.1
Оценка эффективности методов Гаусса
Количество операций умножения и деления
Количество
уравнений
n
Метод Гаусса
с обратным ходом
Метод Гаусса
без обратного хода
1 1 1
2 6 6
3 17 18
Как видно из табл. 4.1, при числе уравнений больше двух метод с обратным
ходом является более экономичным по количеству операций умножения и деле-
ния. Поэтому в стандартных программах, предназначенных для решения систем
линейных уравнений, как правило, используется метод с обратным ходом, причем
его преимущества тем больше, чем больше порядок решаемой системы уравне-
ний.
Метод Гаусса без обратного хода имеет определенные преимущества при
его реализации для получения обратных матриц. Он позволяет вычислять обрат-
ную матрицу со значительно большей эффективностью, чем с помощью классиче-
ского метода.
4.3.4. Влияние округления и погрешности задания исходных данных
на точность решения методом Гаусса
Рассмотренные методы Гаусса являются очень удобными для реализации на
ЭВМ, но их применение не всегда позволяет получить решение с приемлемой
точностью, а в некоторых случаях вообще не позволяет его получить. Причинами
возможности появления большой погрешности могут быть:
- округление результатов вычислений;
- неточность задания исходной информации.
Влияние округления на точность решения связана с особенностями метода и
состоит в том, что при получении коэффициента преобразований
m
на каждом
шаге преобразования уравнений в знаменателе этого коэффициента записывается
главный диагональный элемент матрицы коэффициентов уравнений состояния.
Если на каком либо шаге этот элемент оказывается равным нулю, то даль-
нейшее решение не может быть продолжено, так как в этом случае коэффициент
преобразования оказывается равным
¥
, а эта величина не реализуется на ЭВМ.
Поэтому обычно в алгоритмах предусматривают контроль наличия нулевого эле-
мента в диагонали, и в случае его равенства нулю решение прекращается, что час-
то бывает более приемлемо, чем получение неверного результата в процессе ре-
шения вследствие округления.
Иногда в знаменателе коэффициента оказывается очень маленькое, но зна-
чащее число. Обычно такие маленькие числа могут получиться в процессе вычи-
66
тания двух, близких по значению, но округленных из-за конечной разрядности
ЭВМ, чисел.
Для исключения таких ошибок выполняют такие действия, чтобы диаго-
нальные элементы не были равны нулю. Для этого можно переставить местами
уравнения системы или поменять местами столбцы.
Трудность задачи заключается том, что диагональные элементы рассчиты-
ваются в ходе решения, и нельзя заранее знать, какой из элементов станет нуле-
вым. Поэтому обычно при реализации методов Гаусса на ЭВМ предусматривается
алгоритм выбора главного элемента, в качестве которого выбирают наибольший
из всех коэффициентов уравнений, совершая соответствующую перестановку
строк или столбцов. При таком построении алгоритма, особенно в электротехни-
ческих задачах, как правило, обеспечивается необходимая точность решения.
Для примера рассмотрим решение системы из трех уравнений при точном
представлении результатов вычислений и с учетом округления.
Пусть имеется система из трех уравнений с тремя неизвестными:
.6
23
83
321
321
321
=++
=-+
=
+
+
xxx
xxx
xxx
При представлении величин с точностью до четырех значащих цифр урав-
нения можно записать в виде:
.9999,59999,09999,09999,0
9999,19999,09999,09999,2
9999,79999,09999,09999,2
321
321
321
=++
=-+
=
+
+
xxx
xxx
xxx
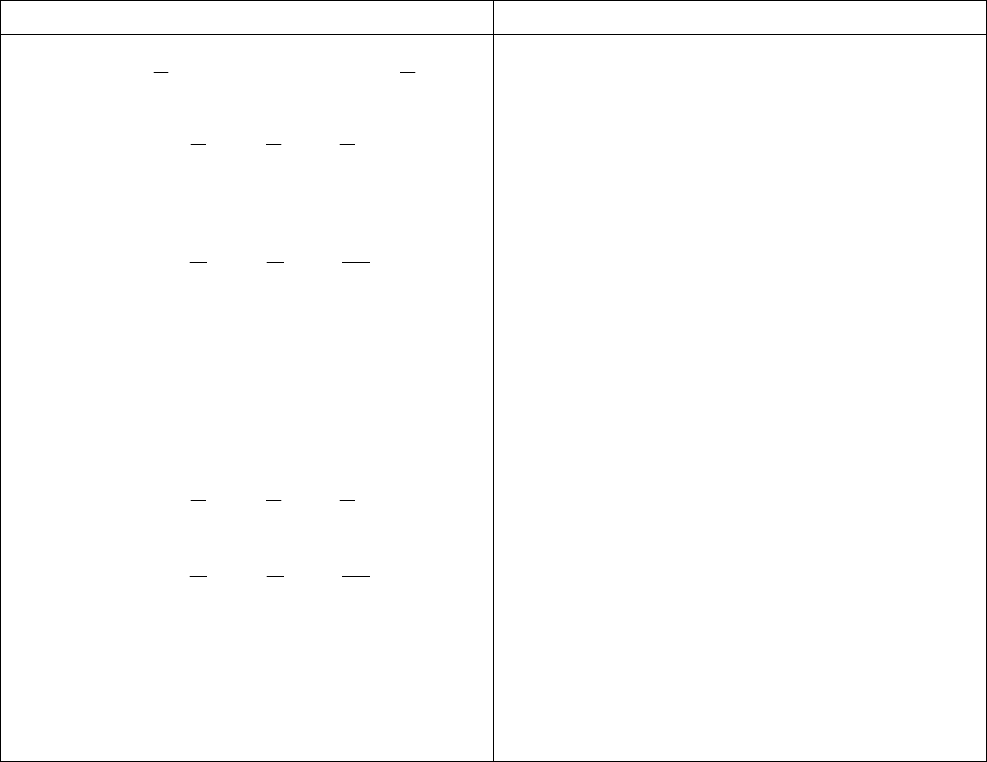
67
Результат решения представлен в таблице 4.2.
Таблица 4.2
Точное При округлении
()
3
1
1
1
=m ;
(
)
1
1
2
=m ;
()
3
1
1
3
=m
3
10
3
2
3
2
0
6200
3
8
3
1
3
1
321
321
321
=++
-=-+
=++
xxx
xxx
xxx
Так как диагональный элемент во вто-
ром уравнении равен нулю, то второй
шаг решения этой системы должен
предусматривать перестановку второго
и третьего уравнений.
6200
3
10
3
2
3
2
0
3
8
3
1
3
1
321
321
321
-=-+
=++
=++
xxx
xxx
xxx
Выполнив второй шаг преобразования,
получим:
123
1
2
3
=
=
=
x;x;x
(
)
33330
1
1
,m = ;
(
)
99990
1
2
,m = ;
(
)
3333,0
1
3
=m
С учетом округления:
3336366670666700
9992599971000100
666723333033330
321
321
321
,x,x,x
,x,x,x
,x,x,x
=++
-=-+
=
+
+
Как видно, в данной системе нет осно-
вания прекращать процесс или пере-
ставлять уравнения в системе, так как
диагональный элемент во второй стро-
ке
(
)
(
)
0
1
22
¹a не равен нулю. Поэтому
выполним второй шаг преобразований.
В результате получим:
ï
þ
ï
ý
ü
-=
=
=
66661
000010
00013
1
2
3
,x
,x
,x
Таким образом, результат получился
абсолютно неправильным.
Помимо округления в ходе решения на точность результата влияет погреш-
ности при задании исходных данных. Они могут быть связаны с двумя случаями:
- неточность определения параметров, входящих в уравнения (коэффициен-
тов и правых частей), связанная с отсутствием точных данных по параметрам
электрических сетей; неправильное составление электротехнической модели рас-
четного режима и, как следствие, математической модели;
- анализ режимов сети, близких к предельным по осуществлению.
Во всех этих случаях может сложиться ситуация, когда матрица коэффици-
ентов системы уравнений плохо обусловлена (ее определитель близок к нулю), т.е.
коэффициенты системы таковы, что в результате небольшой погрешности в зада-
нии информации результаты становятся совершенно неприемлемыми.
Как правило, чтобы ликвидировать большую погрешность результатов, не-
обходимо выполнить проверку обусловленности матрицы коэффициентов. Мат-
рица считается плохо обусловленной, если определитель матрицы много меньше
оценки Адамара
макс
D
:

68
Õå
==
=D£D
n
i
n
j
ij
a
11
2
макс
(4.6)
Если матрица является плохо обусловленной, то либо нужно обеспечить
большую точность задания исходных данных, либо необходимо пересмотреть ма-
тематическую модель сети и сделать ее более точной, либо применить другие ме-
тоды для решения уравнений в случаях, когда рассматриваются задачи с условия-
ми, близкими к предельным по осуществимости.
Для примера рассмотрим систему уравнений:
(
)
,200522001
10021000
21
21
=+
=
+
+
xx
xx
e
где
-
e
погрешность задания коэффициента
11
a .
Решение этой системы можно записать в следующем виде:
e
-
e-
=
e-
=
2
1
20052
21
1
2
1
x
x
.,
;х,х,
;х,х
решенияимеетнесистема50
2003100010
210
21
21
-=e
=-=Þ=e
=
=
Þ
=
e
Причиной такой чрезвычайно высокой чувствительности решения к по-
грешности исходных данных является плохая обусловленность матрицы. Действи-
тельно, ее определитель при
0
=
e
равен:
1
22001
11000
-==D ,
то есть значительно меньше оценки Адамара:
62222
макс
102)22001()11000( ×»+×+=D .
4.4. Применение обратных матриц для решения уравнений
В ряде электротехнических задач приходится многократно решать системы
уравнений при неизменной схеме замещения электроэнергетической системы, на-
пример, при расчете режимов максимальных и минимальных нагрузок, когда за-
даются различные уровни напряжения источников, при изменении нагрузок в уз-
лах.
В таких случаях при использовании метода Гаусса приходится многократно
решать одну и ту же систему уравнений с изменяющимися правыми частями, т.е.
матрица коэффициентов
A
остается неизменной, а в каждом расчете меняются
столбцы правых частей. Таким образом, приходится многократно преобразовы-
вать одну и ту же матрицу.

69
Решение системы уравнений
в
AX
=
можно представить в виде
в
A
X
1-
=
.
Поскольку коэффициенты системы уравнений не меняются, то матрица
1
-
A
вычисляется один раз. Для получения решения относительно неизвестных
X
с
другими правыми частями нужно лишь умножить эту обратную матрицу на новый
столбец правых частей. Так как операция умножения матрицы является более
экономичной по сравнению с операцией решения системы уравнений, то приме-
нение обратной матрицы для многократного решения уравнений также является
более экономичной операцией.
4.4.1. Классический метод получения обратной матрицы
При обращении матрицы (
А
) классическим способом коэффициенты об-
ратной матрицы (
D
) могут быть найдены с помощью следующего выражения:
()
[
]
ji
ij
ij
Аd ×-=
+
1
1
A
, (4.7)
где
-A определитель матрицы
A
;
-
ji
A минор элемента
ji
a в определителе матрицы
A
.
В расчетах рекомендуется использовать следующий алгоритм определения
обратной матрицы классическим способом:
- находят определитель исходной матрицы;
- исходную матрицу транспонируют;
- заменяют каждый элемент транспонированной матрицы его минором;
- меняют знаки у элементов с нечетной суммой индексов;
- каждый элемент полученной матрицы делят на определитель исходной
матрицы.
Для примера рассмотрим решение системы уравнений третьего порядка с
использованием обратной матрицы, полученной классическим способом.
Пусть необходимо решить систему уравнений
.2
932
4
321
321
321
-=--
=++
=
+
+
xxx
xxx
xxx
Запишем матрицу коэффициентов системы:
.
111
132
111
ú
ú
ú
û
ù
ê
ê
ê
ë
é
--
=А
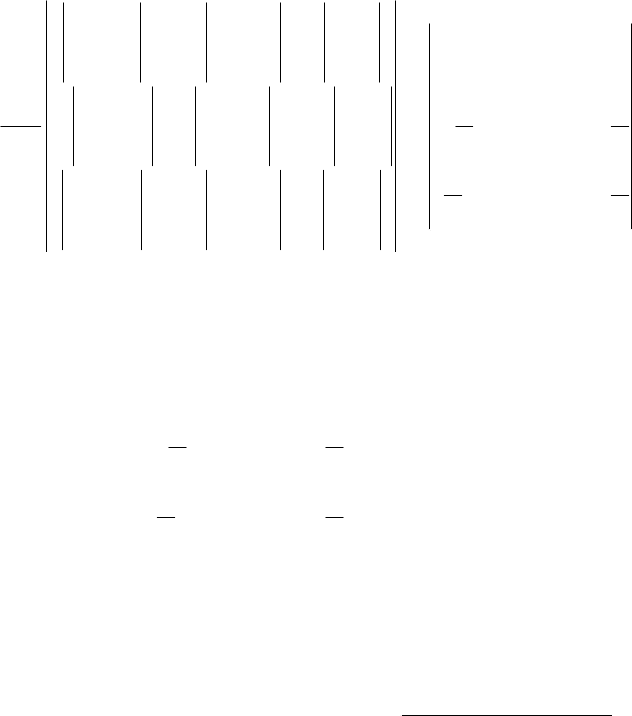
70
Вычислим определитель исходной матрицы:
4
2
1
3
2
1
3
-
=
+
+
-
-
+
-
=
D
.
Тогда в соответствии с выражением (1.117) обратную матрицу
1-
А
получим
в следующем виде:
4
1
5,0
4
5
4
1
5,0
4
3
5,005,0
31
21
11
11
13
12
11
21
11
11
11
12
11
31
11
11
11
13
4
1
1
--
--=
-
-
-
-
--
-
-
-
-
-
-
-
=
-
A .
Для нахождения решения системы уравнений нужно умножить полученную
обратную матрицу на матрицу-столбец правых частей:
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
×
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
--
--=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
1
2
1
2
9
4
4
1
5,0
4
5
4
1
5,0
4
3
5,005,0
3
2
1
х
х
х
.
Классический способ обращения матриц малоэффективен, так как при его
использовании необходимо вычислить определитель n степени и n
2
определителей
(n-1) степени, где n – порядок решаемой системы уравнений.
Вычисление определителя порядка n требует
(
)
(
)
3
31
2
++- nnn
операций
умножения и деления и, в общем случае, близко по трудоемкости к операции ре-
шения системы уравнений, поэтому получение обратной матрицы этим методом
оказывается более трудоемким, чем решение систем уравнений методом Гаусса. В
связи с этим в настоящее время используются другие способы получения обрат-
ных матриц.
4.4.2. Получение обратных матриц с помощью метода Гаусса
без обратного хода
Система из n линейных алгебраических уравнений
в
AX
=
решается методом Гаусса без обратного хода за n шагов, в результате которых ис-
ходная система преобразуется к виду
в
X
A
¢
=
¢
,
