Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей
Подождите немного. Документ загружается.


31
þ
ý
ü
=+
=
+
2222121
1212111
kkk
kkk
EIzIz
EIzIz
(1.40)
Собственные сопротивления представляют собой сумму сопротивлений всех
ветвей, входящих в независимый замкнутый контур.
Взаимные сопротивления представляют собой сумму сопротивлений ветвей,
по которым совместно протекают контурные токи. В данном случае это одно со-
противление
3
z , по которому протекают токи контуров 1 и 2. Если контуры не
имеют общих сопротивлений, то взаимные сопротивления равны нулю.
Если положительные направления контурных токов в общей ветви совпада-
ют, то общее сопротивление берется со знаком “ + ”, в противном случае – со зна-
ком “ – ” (в данном случае
3
12
zz
-
=
). Если контуры не имеют общих ветвей, то их
общее сопротивление равно нулю.
Контурные ЭДС находятся суммированием ЭДС ветвей, входящих в замкну-
тый контур, с учетом принятых положительных направлений обхода контуров.
Если в схеме присутствуют источники тока, то они могут быть заменены эк-
вивалентными источниками напряжения.
В общем виде уравнения контурных токов можно записать следующим обра-
зом:
ï
þ
ï
ý
ü
=+++
=
+
+
+
knknnnknkn
kknnkk
EIzIzIz
EIzIzIz
K
M
K
2211
11212111
(1.41)
Важным свойством уравнений контурных токов является то, что взаимные
сопротивления коэффициентами уравнений, обладают свойством симметрии, т.е.
jiij
zz
=
. Кроме того, уравнения контурных токов содержат большое количество
нулевых коэффициентов, так как не все замкнутые контуры имеют между собой
взаимные сопротивления. Как и в уравнениях узловых напряжений, данные осо-
бенности уравнений контурных токов могут быть использованы для получения
эффективных алгоритмов решения систем уравнений.
Следует также отметить, что для составления уравнений контурных токов не-
обходимо выделить в схеме независимые контуры. Для сложных схем эта проце-
дура требует большой квалификации расчетчика и плохо формализуется. Она мо-
жет быть формализована лишь с привлечением специальных методов, реализация
которых требует в свою очередь высокой квалификации расчетчика и программи-
ста. Чаще всего метод применяется тогда, когда в схеме присутствуют источники
напряжения, т.к. при наличии источников тока их приходится заменять искусст-
венно источниками напряжения, что усложняет расчет.

32
2. ПРИМЕНЕНИЕ АЛГЕБРЫ МАТРИЦ И ТЕОРИИ ГРАФОВ К РАСЧЕТУ
РЕЖИМОВ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ И СЕТЕЙ
2.1. Общие положения
Расчеты в электроэнергетике связаны с записью систем уравнений высокого
порядка (в настоящее время до нескольких тысяч). В этом случае аналитическое
составление таких уравнений и их преобразование связано с большими трудностя-
ми. Предположим, например, что составляется система из 10 полных уравнений:
ï
ï
þ
ï
ï
ý
ü
=+++
=+++
=+++
nnnnnn
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
K
M
K
K
2211
22222121
11212111
(2.1)
При использовании уравнений в такой форме потребуется записать 100 обо-
значений неизвестных
i
x , перед ними 100 коэффициентов
ij
a , 100 знаков сложе-
ния или вычитания, 10 знаков равенства и 10 свободных членов
i
b . Таким образом,
придется записать 320 символов. При этом, безусловно, необходимыми являются
лишь 100 коэффициентов, 10 свободных членов и, допустим, 50 арифметических
знаков вычитания (“–”). Оставшаяся половина символов лишняя. Нет надобности
повторять символ
1
x во всех первых членах уравнений,
2
x - во всех вторых членах
и т.д. Избежать этого позволяют матричные методы. Они основаны на использова-
нии алгебры матриц и элементов теории графов.
К числу преимуществ матричных методов относятся их большая нагляд-
ность и компактность записи. Они обеспечивают удобную и легко приспосабли-
ваемую к технике расчетов на ЭВМ форму представления параметров элементов
схем замещения сетей и параметров их режимов, оперируя не отдельными вели-
чинами, а группами величин, обладающих общими признаками. Последнее об-
стоятельство позволяет положить в основу расчетов режимов работы сетей ис-
пользование стандартных подпрограмм соответствующих операций с матрицами.
В матричной алгебре каждая из групп большого числа величин может быть
обозначена одним символом, а алгебраические действия с такими символами по-
хожи на обычные действия, известные из элементарной алгебры. Это дает воз-
можность получить аналитически строгие зависимости между группами величин,
в некоторых случаях даже такие, которые в обычной форме получить практически
невозможно. Особенно привлекательно то, что матричные зависимости носят уни-
версальный характер, так как позволяют применить одни и те же методы анализа
как к малому, так и к чрезвычайно большому массиву исходных данных. Поэтому
с их помощью можно выразить в математической форме многие закономерности,
свойственные как малым, так и большим схемам сетей.

33
Под теорией графов понимают область дискретной математики, особенно-
стью которой является геометрический подход к изучению объектов. В конкрет-
ном приложении эта теория исследует свойства и связи явлений или процессов,
которые могут быть интерпретированы геометрическими построениями - графами
(моделями, схемами замещения), свойства которых в дальнейшем подлежат ис-
следованию. Преимуществами этой теории является то, что в связи с простотой
преобразования графов они сравнительно легко позволяют выяснить количест-
венные соотношения между различными параметрами явления или процесса, а
иногда при минимальных затратах дают возможность значительно проще оптими-
зировать рассматриваемую модель.
В существующей практике расчетов режимов сетей особый интерес к тео-
рии графов появился в связи с тем, что она позволяет в ряде случаев упростить
некоторые громоздкие задачи, сложность которых затрудняет их решение обыч-
ными методами. Сочетание преимуществ аналитического представления схем за-
мещения сетей с помощью методов теории графов, позволяющей получить обоб-
щенное представление о сети в матричном виде независимо от ее фактической
структуры, сложности и параметров, с символическими приемами записи и пре-
образования групп величин в алгебре матриц дает возможность выполнить в об-
щем виде все необходимые операции по формированию и решению уравнений со-
стояния в любой из упомянутых выше форм. Кроме того, применение теории графов
во многих случаях позволяет ускорить их решение.
Следует, однако, отметить, что использование матричных методов для рас-
чета очень сложных сетей может быть связано с некоторыми ограничениями. В
первую очередь причина этого состоит в том, что эти методы требуют значитель-
ного объема памяти ЭВМ, что приводит к существенному усложнению расчетов, к
увеличению времени, в течение которого они выполняются , а в некоторых случа-
ях и к невозможности использования ЭВМ для их выполнения. В связи с этим на
современном этапе развитие методов применения теории графов и матричной ал-
гебры в области анализа режимов работы сетей в первую очередь направлено на
изыскание способов уменьшения объемов вычислительной работы при реализа-
ции этих методов с помощью ЭВМ. Это особенно важно для сложных схем.
2.2. Некоторые сведения из алгебры матриц
Матрицей в общем случае называют упорядоченную запись ее элементов,
располагаемых в определенной последовательности в форме условной таблицы:
А =
é
ë
ê
ê
ê
ù
û
ú
ú
ú
аа а
aa a
aa a
m
m
n n nm
11 12 1
21 22 2
1 2
K
K
K KKK
K
. (2.2)
Элементами матрицы могут быть числа любого вида или даже функции од-
ной или нескольких переменных; их запись в форме матрицы не предусматривает
34
каких-либо действий над ними. В матрице элементы располагаются по строкам и
столбцам, поэтому любая матрица имеет прямоугольную (иногда квадратную)
форму. Элементы каждой строки, а также каждого столбца обладают каким-либо
общим свойством.
Алгебра матриц определяет алгебраические операции над массивами эле-
ментов описанного типа; при этом предполагается, что каждый массив представ-
ляет собой единое целое, в связи с чем он может быть обозначен одним символом.
Алгебраические операции осуществляются с отдельными элементами, содержа-
щимися внутри массива, и все же предметом алгебры матриц являются действия с
самими массивами, которые выступают в ней в качестве обособленных и целост-
ных систем.
На практике все элементы матрицы обычно обозначают одной буквой. По-
ложение элементов в матрице определяется двумя индексами, записанными ря-
дом; первый из них (
i
) обозначает строку, а второй (
j
) - столбец, которым при-
надлежит данный элемент. Такие обозначения позволяют в весьма компактной
форме записать не только элементы строк и столбцов, но и целые матрицы. На-
пример, матрицу (1.43) можно записать в следующем виде:
{
}
А = а
ij
при
i
n
=
1
2
,
,
,
K
и
j
m
=
1
2
,
,
,
K
. (2.3)
При проведении операций над матрицами большое значение имеет их поря-
док - размерность. Порядок матрицы определяется числом ее строк и столбцов.
Так, матрица А в соответствии с (2.2), имея n строк и m столбцов, имеет порядок
n
m
*
.
Если элементы матрицы записаны в форме одного столбца:
А =
é
ë
ê
ê
ê
ù
û
ú
ú
ú
а
a
a
n
1
2
K
, (2.4)
то такая матрица называется матрицей-столбцом (столбцовой) или вектором-
столбцом.
В том случае, когда элементы матрицы записаны в форме одной строки:
[
]
А
=
аа а
m
1
2
K
, (2.5)
то такая матрица называется матрицей-строкой (строчной) или вектором-
строкой.
Матрица, состоящая из нескольких строк и столбцов, как, например, (2.2),
называется прямоугольной.
Как видно из (2.4) и (2.5), элементы столбцовой и строчной матриц имеют
один индекс - соответственно i или j. Элементы прямоугольной матрицы снабжа-
ют двумя индексами - i и j.
Если число строк матрицы n равно числу столбцов m, то такую матрицу на-
зывают квадратной. В этом случае элементы а
11
, а
22
, ..., а
nm
, находящиеся на пе-
ресечении строк и столбцов, отмеченных одинаковыми номерами, считаются рас-
положенными на главной диагонали и называются диагональными.
35
Когда элементы квадратной матрицы, расположенные симметрично относи-
тельно главной диагонали, одинаковы (а
ij
=а
ji
), то такая матрица называется сим-
метричной.
Если же указанные элементы, кроме того, равны нулю, то матрица называ-
ется диагональной.
Диагональная матрица, каждый из диагональных элементов которой равен
единице, называется единичной:
1 =
é
ë
ê
ê
ê
ù
û
ú
ú
ú
1000
0100
0010
0001
. (2.6)
В практике матричных операций находят также применение единичная мат-
рица-столбец n :
n =
é
ë
ê
ê
ê
ù
û
ú
ú
ú
1
1
1
K
(2.7)
и транспонированная относительно нее единичная матрица-строка n
t
:
[
]
n
t
=
11 1
K
. (2.8)
Транспонированной матрицей A
t
размером
m
n
*
относительно матрицы A
размера
n
m
*
называется матрица, получаемая из матрицы A заменой ее строк со-
ответствующими столбцами. Например, если A имеет вид (2.2), то транспониро-
ванную относительно нее получим в виде:
А
t
n
n
m m nm
а а а
a a a
a a a
=
é
ë
ê
ê
ê
ù
û
ú
ú
ú
11 21 1
12 22 2
1 2
K
K
K KKK
K
. (2.9)
Две матрицы считаются равными в том случае, если каждый элемент одной
матрицы равен соответствующему элементу другой матрицы, т.е. А = В, если
{a
ij
}={b
ij
}, иными словами, если a
ij
=b
ij
при i = 1,2,...n и j = 1,2,...m. Таким образом,
утверждение о равенстве матриц не имеет смысла, если у них разные порядки.
Алгебраическим сложением двух матриц называется операция, при которой
алгебраически складываются соответствующие элементы матриц-слагаемых,
имеющих одинаковый порядок:
САВ=+=
é
ë
ê
ê
ù
û
ú
ú
+
é
ë
ê
ê
ù
û
ú
ú
=
+
+
+ +
+ +
é
ë
ê
ê
ù
û
ú
ú
а а
а а
а а
b b
b b
b b
a b a b
a b a b
a b a b
11 12
21 22
31 32
11 12
21 22
31 32
11 11 12 12
21 21 22 22
31 31 32 32
. (2.10)
Произведение скалярной величины (числа) на матрицу представляет собой
матрицу, в которой каждый элемент матрицы-множителя умножается на скаляр-
ную величину-множимое:

36
В А=×=
é
ë
ê
ê
ù
û
ú
ú
l
l
l
l l
l l
а а
а а
а а
11 12
21 22
31 32
. (2.11)
Операцией умножения двух матриц (множимой и множителя) называют та-
кое действие, при котором в качестве элементов, расположенных на пересечении
i-й строки и j-го столбца матрицы-произведения, помещаются суммы попарных
произведений элементов, расположенных на соответствующих местах i-х строк
матрицы-множимого и j-х столбцов матрицы-множителя:
.
322322221221
321322121211
312321221121
311321121111
3231
2221
1211
232221
131211
ú
û
ù
ê
ë
é
++
++
++
++
=
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
´
ú
û
ù
ê
ë
é
=´=
bababa
bababa
bababa
bababa
bb
bb
bb
ааа
ааа
ВАС
(2.12)
Результатом перемножения является матрица, число строк которой равно
числу строк матрицы-множимого, а число столбцов - числу столбцов матрицы-
множителя.
В общем случае операция умножения не обладает переместительным свой-
ством, т.е.
А
В
В
А
´
¹
´
. (2.13)
Матрица А
-1
, в результате умножения которой на матрицу А, произведение
оказывается равным 1, называется обратной к матрице А:
А
-1
´
А = 1. (2.14)
Очевидно, что последнее соотношение имеет место только в том случае, ко-
гда матрицы А и А
-1
- квадратные. Следовательно, любая прямоугольная матрица
обратной не имеет.
Таким образом, любое из уравнений состояния можно записать в матричной
форме:
В
Х
А
=
×
, (2.15)
где А – матрица коэффициентов уравнений состояния, квадратная, неособенная,
так как отвечает системе независимых уравнений; Х – столбцовая матрица неиз-
вестных уравнений состояния; В – столбцовая матрица вынуждающих сил.
Учитывая особенности операции умножения матриц, можно записать:
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
´
ú
ú
ú
û
ù
ê
ê
ê
ë
é
3
2
1
3
2
1
333231
232221
13
1211
b
b
b
x
x
x
aaa
aaa
aaa
. (2.16)
После перемножения матриц получим:
ï
þ
ï
ý
ü
=++
=++
=
+
+
3333232131
2323222121
1313212111
bxaxaxa
bxaxaxa
bxaxaxa
(2.17)
37
Задача применения матричной алгебры состоит в том, чтобы формализовать
запись указанных уравнений. Обычно это производят с применением теории гра-
фов и методов исследования топологии сети. После завершения формирования
уравнений их решают либо непосредственно с помощью применения численных
методов, либо с привлечением методов обращения матриц коэффициентов.
Например, пусть имеется система уравнений
В
Х
А
=
×
. (2.18)
Умножив обе части уравнения (2.18) на А
-1
слева и учитывая, что произведение
взаимно обратных матриц дает единую матрицу (А
-1
´
А = 1), получим:
В
А
Х
-1
×
=
(2.19)
Следует, однако, отметить, что, несмотря на кажущуюся простоту решения
матричного уравнения, объем вычислений по этому решению остается достаточно
большим. Причем, наибольшие трудности связаны с нахождением обратной мат-
рицы. Однако, независимо от сложности технического выполнения этой операции,
сама запись матричных преобразований с ее использованием значительно упроща-
ет решение задач в общем виде.
Для решения конкретных задач матричным методом, в том числе и для запи-
си уравнений состояния в символическом виде, необходимо иметь аналитическое
описание схемы соединения ветвей и схемы замещения системы. Это описание
может быть получено при использовании некоторых представлений топологиче-
ской теории графов.
2.3. Схема замещения сети как связанный направленный граф
Конфигурацию схемы замещения электрической системы можно отобразить
в виде графа.
В электротехнике основы применения теории графов были заложены Кирх-
гофом в средине XIX века. Он показал, что при составлении уравнений состояния
электрической цепи последнюю удобно представить графом, с помощью которого
и находить линейно независимые системы контуров путем выделения в графе его
деревьев. Такой подход позволяет формализовать составление уравнений состоя-
ния, облегчив реализацию расчетов режимов больших схем на ЭВМ, особенно в
электроэнергетике.
Под графом электрической сети понимают геометрическое построение,
отображающее конфигурацию схемы замещения электрической системы, а также
все связи этой системы. При этом ветвям схемы ставятся в соответствие ребра гра-
фа, а узлам схемы – вершины графа.
Ребро – это линия, имеющая две конечные точки. Оно может быть направ-
ленным, если для линии задано направление из одной точки в другую. Оно не обя-
зательно должно быть прямой линией, но не пересекает само себя, т.е. не имеет
общих точек. В электротехническом смысле ребро может обозначать ветвь с со-
противлением, выпрямителем и т.д. В общем случае ребру могут приписываться и
38
другие значения, например, ребро может означать процесс между двумя состоя-
ниями.
Если ветви графа имеют направление, то граф называется направленным.
Совокупность всех ребер, соединяющих две одинаковые точки, называют
кратными ребрами (параллельными ветвями).
Вершина – это конечная точка ребра или одна изолированная точка. В элек-
тротехническом смысле вершинам соответствуют узлы схемы замещения.
Если в схеме имеются замкнутые контуры, то ее граф называется замкнутым
(в противном случае – разомкнутым).
Любая совокупность вершин и ребер, выделенных из исходного графа, на-
зывается подграфом (частичным графом).
Совокупность ребер, соединяющих две произвольные вершины, называется
путем графа. Если начальная и конечная вершины пути графа совпадают, то этот
путь графа является замкнутым и образует контур. Под длиной пути понимают
число ребер пути. Если в графе можно выбрать путь, который соединяет его лю-
бые две вершины, то этот граф является связанным, если нельзя – несвязанным.
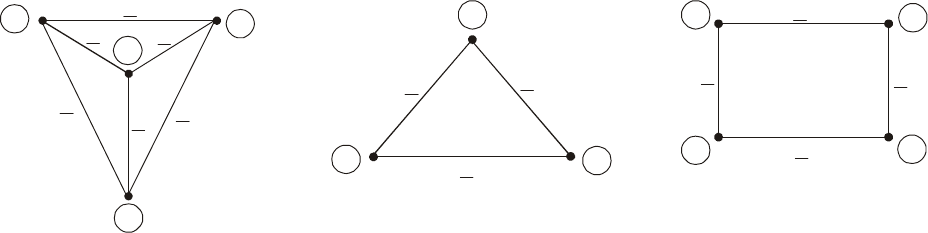
На рис.2.1 приведены примеры связанного (а) и несвязанного (б) графов.
Рис.2.1
Как уже отмечалось, если ветви графа имеют направления, то граф является
направленным. В этом случае каждое ребро графа имеет начальную и конечную
вершины, и его направление принимается от начальной вершины к конечной.
Наиболее распространенными выделенными совокупностями графа являют-
ся дерево и хорды графа. Подграфом дерева называется совокупность ветвей гра-
фа, соединяющих между собой все вершины графа без образования замкнутых
контуров. (Иными словами, дерево – это разомкнутая часть замкнутой схемы,
включающая все узлы схемы). Подграф, дополняющий подграф дерева до полного
графа схемы сети, называют подграфом хорд. Этот подграф фактически замыкает
независимые контуры. В частном случае, если граф представляет собой разомкну-
тую схему, т.е. в нем отсутствуют замкнутые контуры, он состоит только из под-
графа дерева.
1
2
4
3
1
5
2
3
6
4
1
2
3
3
1
2
7
4
5
6
7
4
5
6
а) связанный граф
б) несвязанный граф
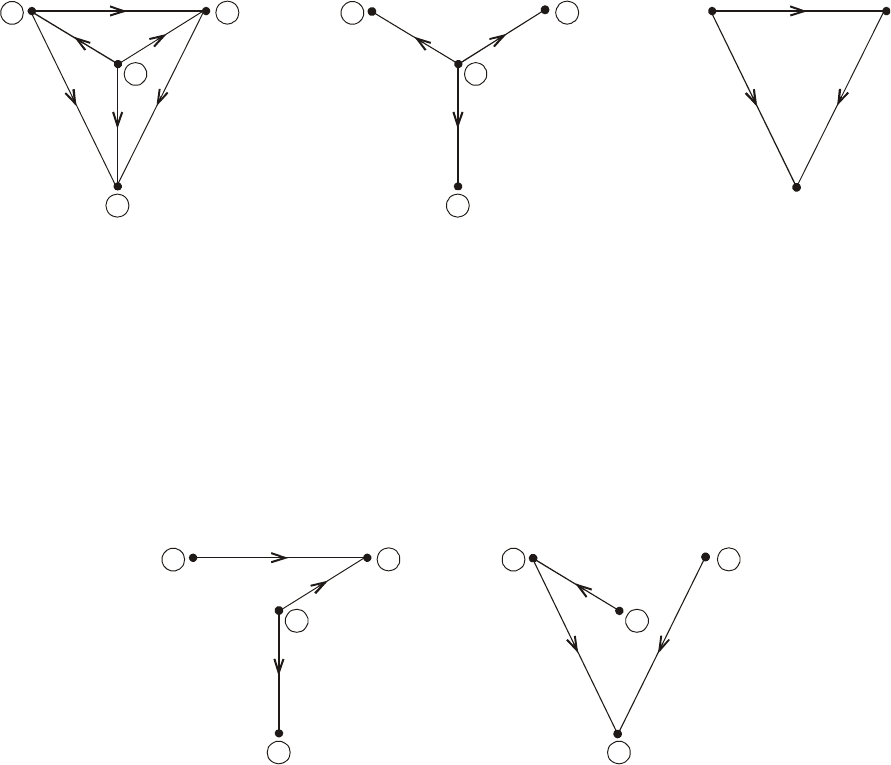
39
Рис.2.2 Выделение дерева и хорд графа
Граф можно разделить на дерево и хорды по-разному. На рис.2.3 показан
еще один из вариантов выделения дерева и хорд в графе рис.2.2:
Рис.2.3 Вариант выделения дерева и хорд графа
Обычно выбирают такой алгоритм выделения подграфа дерева, который по-
зволяет при выделении подграфа хорд считать, что каждая хорда замыкает один
независимый контур, и эти контуры называют системой базисных контуров графа.
Из приведенных выше кратких теоретических сведений теории графов мож-
но сделать вывод, что схема замещения электрической сети может отображаться в
виде графа. Схема замещения сети обычно отображается связанным графом. Он
состоит из ветвей, соединенных в узлы. Эти ветви образуют цепочки (пути графа),
которые могут замыкаться и образовывать тем самым замкнутые контуры. Все ве-
личины, характеризующие состояние ветвей, имеют определенные направления
(ЭДС, напряжения, токи), в связи с чем целесообразно каждой ветви схемы при-
дать произвольно определенное направление. Таким образом, схема замещения се-
ти является связанным направленным графом, ребрами которого являются ветви, а
вершинами узлы.
б) подграф - дерево
в) подграф хорд
1 12
2
4
4
3
3
1
1
4
4
3
3
2
2
5
5
6
6
а) полный граф
подграф хорд
подграф дерева
1
1
2
2
4
4
3
3
1
4
3
2
5
6
40
2.4. Матрицы соединений графа электрической сети
Направленный граф может быть аналитически отображен с помощью первой
и второй матрицы инциденций (соединений), наличие которых позволяет записать
в символьном виде уравнения состояния электрической сети.
2.4.1. Матрица соединений ветвей графа в узлах
(первая матрица инциденции)
Первая матрица инциденции служит для обобщенного аналитического
представления соединений ветвей в узлах направленного графа.
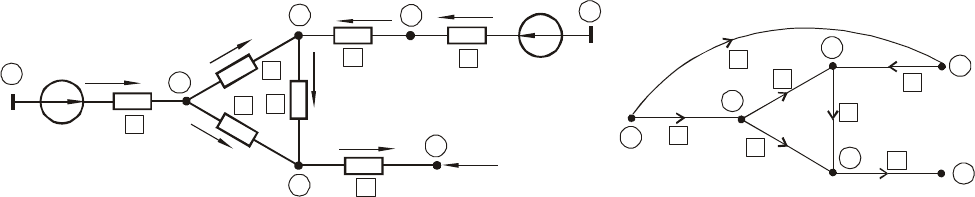
Для пояснения принципов составления первой матрицы инциденций рас-
смотрим схему сети и отвечающий ей направленный граф, изображенные на рис.
2.4.
Рис. 2.4 Пояснения к составлению первой матрицы инциденций
Уравнения по первому закону Кирхгофа с учетом токов всех ветвей можно
записать в следующем виде.
Для узла 1: 00100011
7
6
5
4
3
2
1
=
×
+
×
+
×
+
×
+
×
+
×
+
×
-
IIIIIII
(2.20)
Для узла 2: 00010110
7
6
5
4
3
2
1
=
×
+
×
+
×
+
×
+
×
-
×
-
×
IIIIIII
И так далее для всех узлов.
Таким образом, для каждого узла i можно записать:
0
=
×
S
ijij
Im (2.21)
Нетрудно отметить, что токи ветвей входят в уравнения (2.20) с коэффици-
ентами 1; -1; 0. Эти коэффициенты, называемые коэффициентами соединений
(инцидентности), используют при составлении первой матрицы инциденций.
В первой матрице инциденций строки отвечают номерам узлов, а столбцы -
номерам ветвей. На пересечении строки i и столбца j располагают коэффициент
соединений, который равен 1, если ветвь j соединена с узлом i своей начальной
вершиной (имеет направление от узла i); -1, если ветвь j соединена с узлом i своей
конечной вершиной (направлена к узлу i); 0, если ветвь j не связана с узлом i.
6
1
1
4
4
2
2
3
5
5
7
7
5
1
3
1
4
2
3
4
6
6
6
2
6
5
3
I
I
I
I
I
I
I
1
2
4
7
5
3
6
а) схема сети
б) граф сети
