Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей

Подождите немного. Документ загружается.

Соответственно комплексы рассмотренных выше напряжений можно пред-

ставить в виде:

;UjUU

вi

(1.10)

;UjUU

фф

(1.11)

;UjUU

(1.12)

где

вi

U,U

- соответственно активные составляющие этих напряжений, а

фвi

U,U

- их реактивные составляющие.

Для токов элементов, а также токов узлов, получим:

;IjII

(1.13)

где

- активная составляющая тока;

- его реактивная составляющая.

Согласно принятым обозначениям, полная мощность одной фазы будет рав-

на:

,IUS

фф

= (1.14)

где

I - сопряженный комплекс тока.

Полная мощность трех фаз:

jQPIUSS

фф

+=== 33 , (1.15)

где

- активная и реактивная мощности трех фаз.

Модуль полной мощности может быть найден также с помощью выражения:

UIS 3= (1.16)

Из (1.15) и (1.16) следует, что

j= cosUIP 3 ; (1.17)

j= sinUIQ 3 , (1.18)

где

- угол между векторами тока и напряжения.

В соответствии с (1.15) ток в узле и его составляющие получим в виде:

( )

фф

UjU

jQP

¢¢

, (1.19)

фф

UQUP

; (1.20)

UQUP

. (1.21)

Квадрат модуля тока, согласно (1.17) и (1.19) можно выразить следующим

образом:

I = (1.22)

Соответственно потери полной мощности в сопротивлении элемента будут

равны:

zIS

3 ==D (1.23)

Как правило, результаты расчетов представляются в трехфазных мощностях,

фазных токах и линейных напряжениях.

1.5. Применение уравнений законов Кирхгофа

Обычно постановка задачи расчета установившихся режимов работы ЭЭС

такова, что в качестве независимых переменных принимаются токи и напряжения

ветвей, а также контурные токи или узловые напряжения, т.е. напряжения в узлах

по отношению к какому-либо узлу, напряжение в котором принимается за задан-

ное. Известными считаются полные сопротивления или проводимости всех пас-

сивных элементов электрической цепи, ЭДС, действующие в ветвях, и задающие

источники токов в узлах.

“Прямой” метод расчета режима ЭЭС состоит в непосредственном приме-

нении уравнений первого и второго законов Кирхгофа. Как известно, на основа-

нии этих законов для электрической цепи произвольной конфигурации, содержа-

щей

ветвей,

независимых узлов и

независимых контуров, может быть со-

ставлена система

(1.24)

взаимно независимых уравнений относительно неизвестных токов ветвей вида:

увi

(1.25)

åå

вjвj

вj

EIz

(1.26)

Эти уравнения называются также уравнениями состояния электрической це-

пи или ЭЭС.

Уравнение вида (1.25) должны быть составлены для независимых узлов це-

пи. Узел, исключаемый из рассмотрения, получил название узла баланса или ба-

лансирующего узла. Баланс его токов может быть получен в результате сумми-

рования токов других узлов.

В расчетах режимов ЭЭС в качестве балансирующего узла чаще всего при-

нимается либо узел нулевого потенциала, либо узел, отвечающий шинам мощной

узловой подстанции или станции, осуществляющей балансирование потоков

мощности в сети или в электросистеме.

Уравнения вида (1.26) должны быть составлены для

независимых конту-

ров цепи. При этом под независимым контуром понимают такой контур, в кото-

рый входит хотя бы одна ветвь, не входящая в другие контуры. Для цепи, содер-

жащей

ветвей и

независимых узлов, число независимых контуров или, что то

же самое, число взаимно независимых уравнений, которые могут быть составлены

на основании второго закона Кирхгофа в соответствии с (1.24), можно определить

как:

Следует отметить, что при записи уравнений состояния ЭЭС по первому и

второму законам Кирхгофа правильный выбор независимых контуров является

важной и самой трудоемкой операцией. Она особенно труднореализуема примени-

тельно к сложным ЭЭС, которые могут иметь сотни и тысячи контуров.

Для того, чтобы определить число независимых контуров в цепи, необходи-

мо “ разорвать” все ее ветви, замыкающие эти контуры (разорвать “хорды”), так,

чтобы цепь превратилась в разомкнутую. Число разорванных ветвей и будет рав-

но числу независимых контуров.

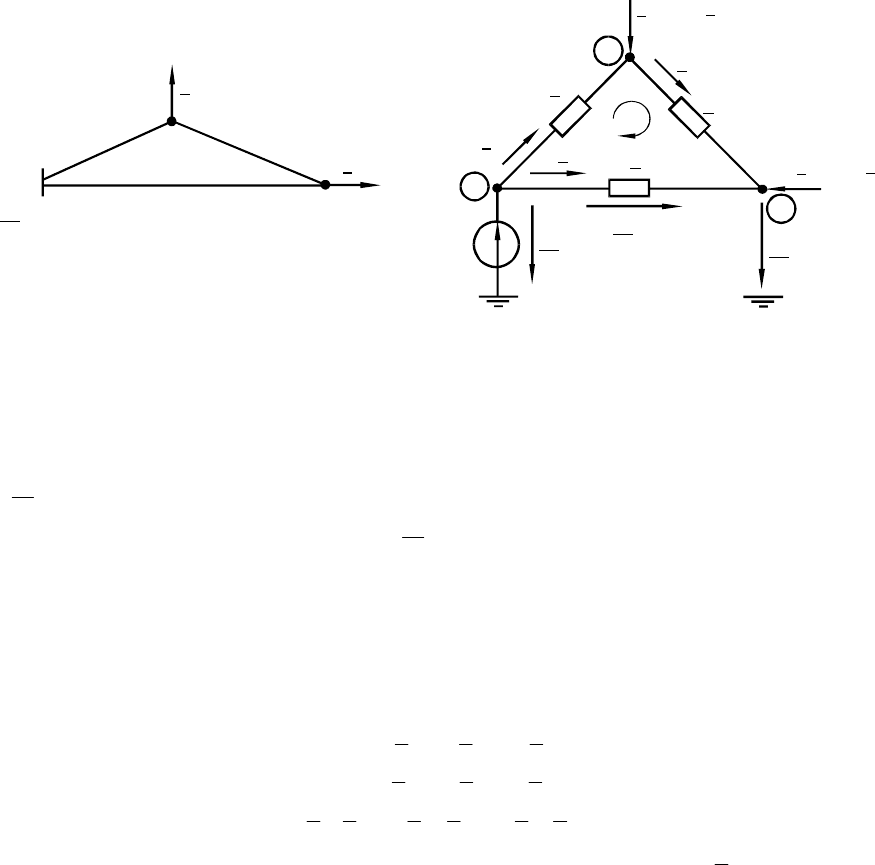
Для примера составим уравнения для расчета режима простейшей ЭЭС,

изображенной на рис.1.10, воспользовавшись для этого законами Кирхгофа и Ома.

Рис.1.10 а) схема сети; б) расчетная схема замещения.

Схема замещения сети рис.1.10, а приведена на рис.1.10, б. Примем, что

U - линейное значение напряжения на шинах узловой подстанции, от которой

питается сеть, и, кроме того, что

U - задано относительно узла нулевого потен-

циала.

Будем считать, что балансирующим является узел 3, тогда в соответствии с

первым законом Кирхгофа для цепи рис.1.10, б могут быть составлены два взаим-

но независимых уравнения для узлов 1 и 2, а в соответствии со вторым – одно, для

контура I:

=-+

=--

.IzIzIz

;III

вввввв

увв

332211

232

121

(1.27)

Решив систему (1.27), получим значения токов ветвей

вi

I .

Л1

Л3

Л2

const

а)

б)

Далее, используя закон Ома (1.1), можно определить падения напряжений

на ветвях:

вiвi

вi

IzU

Потери мощности в ветвях будут равны:

вi

вiвi

IUS 3=D .

Линейное напряжение, например, в узле 2 в соответствии со вторым зако-

ном Кирхгофа получим следующим образом:

вc

UUU .

Таким образом, число уравнений состояния, которые должны быть состав-

лены для ЭЭС с целью расчета ее режима по первому и второму законам Кирхго-

фа, равно числу ветвей электрической цепи ее схемы замещения. Этот метод пре-

дусматривает необходимость выделения независимых узлов и независимых кон-

туров цепи. Последнее для сложной ЭЭС является весьма трудоемкой операцией.

В то же время известно, что расчеты установившихся режимов ЭЭС могут быть

произведены и с помощью более эффективных методов, позволяющих, например,

снизить число решаемых уравнений. Такими методами являются метод узловых

напряжений и метод контурных токов.

1.6. Уравнения узловых напряжений

Уравнения узловых напряжений в электротехнике известны под названием

уравнений узловых потенциалов. Как уже отмечалось, при анализе и расчетах

симметричных рабочих режимов ЭЭС считается, что потенциал трехфазной цепи

или , что в этом случае то же самое, потенциал земли

, равен нулю. По-

этому, если после составления и решения уравнений узловых потенциалов отно-

сительно потенциалов цепи

также напряжения в узлах ЭЭС

фi

U определяются

относительно нулевого потенциала, то справедливо следующее выражение:

iNi

фi

В этом случае при составлении уравнений узловых потенциалов и их преоб-

разовании удобно оперировать непосредственно с понятиями напряжений, назы-

вая соответственно и уравнения – уравнениями узловых напряжений.

Уравнения узловых напряжений вытекают из первого закона Кирхгофа и за-

кона Ома, если все токи в ветвях выразить через напряжения узлов и проводимо-

сти ветвей. Например, для цепи, изображенной на рис.1.10, б, полная система

уравнений узловых напряжений, записанная на основании первого закона Кирх-

гофа, будет иметь вид:

=++

,IUYUYUY

;IUYUYUY

ффф

(1.28)

где

фi

U неизвестные фазные значения узловых напряжений;

уi

I задающие токи в узлах;

Y собственные проводимости узлов;

Y взаимные проводимости между узлами

(

);

- текущие номера узлов.

Взаимная проводимость между двумя любыми узлами

равна взятой с

обратным знаком сумме проводимостей ветвей, соединяющих эти узлы. Напри-

мер, если узлы

соединены одной ветвью с сопротивлением

z и проводимо-

стью

Y , то

вij

-=-= (1.29)

Если между двумя узлами в схеме цепи нет ветвей, то соответствующая вза-

имная проводимость равна нулю.

Собственная проводимость

узла

Y равна сумме проводимостей всех вет-

вей, соединенных с узлом

, т.е. сумме взаимных проводимостей ветвей

Y , свя-

занных с этим узлом, взятой с обратным знаком. Пусть с узлом

соединено

вет-

вей, тогда

åå

-==

врii

YYY , (1.30)

где

(

)

1n общее число узлов в сети, из которых

независимы.

Для рассматриваемой сети из трех узлов, например:

( )

+-=-=

1312111

YYYY .

Задающие токи узлов

уi

I равны алгебраической сумме токов источников,

подключенных к узлу

. Как уже отмечалось, токи, соответствующие генерации,

принимаются с положительным знаком, потреблению – с отрицательным. При

наличии в цепи источников ЭДС в ток

го узла

уi

I входит алгебраическая сума

произведений ЭДС ветвей, соединенных с узлом

на проводимости этих ветвей.

Очевидно, что, поскольку полная система (1.28) записана на основании пер-

вого закона Кирхгофа для всех

узлов цепи, то она представляет собой систе-

му линейных зависимых уравнений. Сумма всех токов узлов в ней будет равна ну-

лю, а полная матрица узловых проводимостей, если только в ней не учитываются

проводимости на землю, является симметричной и вырожденной (ее определитель

равен нулю).

Уравнения (1.28) решаются следующим образом. Один из узлов цепи, на-

пример

(

)

1n й, принимается за базовый по напряжению и балансирующий по

току. Напряжение в этом узле

( )

1+nфб

U предполагается известным (опорным, ба-

зисным), а ток

( )

1+nу

I - неизвестным и равным сумме токов остальных

узлов.

Токи в остальных

узлах считаются заданными, а напряжения неизвестными.

В результате, отбросив

(

)

1n е уравнение в вырожденной системе (1.28),

получим следующую систему взаимно независимых уравнений, подлежащих ре-

шению:

-=+

,UYIUYUY

;UYIUYUY

фб

бу

фф

фб

бу

фф

(1.31)

где

3ффб

UU известное напряжение базового узла;

232131

YY;YY

бб

Или в общем виде:

-=+++

фб

nбуn

фn

фб

бу

фn

фф

UYIUYUYUY

111

(1.32)

Следует отметить, что в общем случае базовым по напряжению и баланси-

рующим по току могут быть и разные узлы.

Для цепи, в которой в качестве базисного узла принимается узел нулевого

потенциала (нейтрали, земли),

фб

U , поэтому уравнения (1.32) примут вид:

=+++

уn

фn

фф

IUYUYUY

(1.33)

Умножив левые и правые части уравнений (1.32) и (1.33) на

3 , можно по-

лучить соответствующие системы уравнений, записанные относительно между-

фазных значений напряжений. Например, преобразуя (1.32), получим:

-=+++

,UYIUYUYUY

;UYIUYUYUY

nбуn

nnnn

бу

111

(1.34)

где

фббфii

UU;UU 33 == .

Анализируя уравнения (1.31) – (1.34), нетрудно заметить, что после выделе-

ния базового узла и перехода к системам взаимно независимых уравнений узло-

вых напряжений собственные проводимости независимых узлов

Y продолжают

сохранять в своем составе проводимости ветвей, соединяющих

й узел с базо-

вым. Следовательно, для взаимных проводимостей между узлами

и базовым

справедливо следующее соотношение:

( )

-+-=

ijiiiб

YYY

(1.35)

Например, для систем (1.31) можно записать

1211131

YYYY

Учитывая (1.35) в уравнениях (1.34), им можно придать еще более общую

форму:

-=+++

DDD

,UYIUYUYUY

;UYIUYUYUY

nбуn

nnnn

бу

111

(1.36)

где

(

)

бiфбфii

UUUUU -=-=

3 .

Очевидно, что уравнения (1.33) – это частный случай (1.36) при 0

U , за-

писанный для фазных значений напряжений.

Из (1.36) следует, что при уменьшении напряжения базисного узла и напря-

жений всех других узлов на одну и ту же величину при неизменных заданных то-

ках узлов разности напряжений между узлами не изменяются. Токи в ветвях, ко-

торые равны разностям напряжений между узлами, умноженным на проводимости

ветвей, при изменении напряжений всех узлов на одну и ту же величину в линей-

ной цепи также не изменяются. Это справедливо и для потерь мощности в ветвях.

Можно показать, что напряжения в узлах и токи в ветвях не зависят от того,

какой узел линейной электрической цепи выбирается в качестве балансирующего

по току, если сумма токов во всех

узлах равна нулю. Поэтому выбор баланси-

рующего узла, а также его напряжения (например, 0

U или 0

U ) не оказы-

вают влияния на результат расчета установившегося режима линейной цепи. В

этом линейные уравнения узловых напряжений (1.33) и (1.36) эквивалентны.

Для нелинейных уравнений установившегося режима выбор балансирующе-

го узла и значение его напряжения оказывают влияние на результат расчета ре-

жима. Поэтому при нелинейных задающих токах в узлах уравнения (1.33) и (1.36)

не эквивалентны. При расчетах нелинейных уравнений установившихся режимов

ЭЭС используются уравнения узловых напряжений (1.36), так как обычно в каче-

стве балансирующего узла применяется станция, ведущая по частоте, напряжение

которой, конечно, не равно нулю.

Уравнения, записанные в форме (1.32) – (1.34) и (1.36), получили название

уравнений баланса токов. Если эти уравнения умножить на сопряженные ком-

плексы напряжений узлов, для которых записано каждое из уравнений, то систе-

мы приобретут вид уравнений балансов мощностей. Например, уравнения (1.36)

приобретут в этом случае вид:

=+++

DDD

SUUYUUYUUY

(1.37)

В некоторых случаях уравнения, записанные относительно мощностей уз-

лов, оказываются более удобными для выполнения расчетов.

Уравнения (1.37) в более наглядной форме иллюстрируют нелинейность в

общем случае уравнений установившихся режимов ЭЭС. Поскольку мощности в

узлах

S зависят от напряжений этих узлов, а напряжения в свою очередь являют-

ся искомыми величинами в уравнениях (1.37), то правые части уравнений зависят

от нескольких переменных, и уравнения являются нелинейными. Кроме того, т.к.

после решения данной системы уравнений и определения напряжений в узлах од-

нозначно определяются ток в ветвях и мощности в начале и в конце каждой ветви,

то заключение о нелинейности можно отнести не только к задаче определения на-

пряжений, но и ко всей задаче расчета установившихся режимов электроэнергети-

ческих систем и сетей при задании нагрузки неизменными мощностями.

Уравнения узловых напряжений позволяют рассчитать режим ЭЭС на осно-

вании системы, составленной только для независимых узлов электрической цепи

ее схемы замещения. Как правило, в современных ЭЭС предельное число незави-

симых узлов

в 1,5 раза меньше числа ветвей

Взаимные проводимости узлов, являющиеся коэффициентами уравнений

узловых напряжений, обладают свойством симметрии, т.е.

jiij

. Важнейшим

их свойством является также то, что среди них находится большое количество ну-

левых элементов. Как отмечалось выше, если узлы не соединены между собой

ветвью, то их взаимная проводимость равна нулю. В ЭЭС каждый узел связан

лишь с небольшим числом узлов. Как правило, большинство узлов соединены со

значительно меньшим числом узлов, чем 10. Симметрия коэффициентов уравне-

ний узловых напряжений и равенство значительного их числа нулю позволяют ра-

ционально использовать память ЭВМ при их решении и запоминать столько нену-

левых взаимных проводимостей, сколько ветвей в ЭЭС, и столько собственных

проводимостей узлов, сколько в ней независимых узлов. Это дает возможность

увеличить объем решаемых задач или увеличить скорость их решения при одном

и том же объеме.

Например, если в ЭЭС, схема замещения которой состоит из 100 независи-

мых узлов, первый узел связан с 10 другими, то в первом уравнении окажется

только 10 ненулевых проводимостей, а остальные 90 будут равны нулю. То же са-

мое, из 100 коэффициентов при первом неизвестном во всех уравнениях лишь 10

будут ненулевыми, а 90 – будут равны нулю. На этом примере можно убедиться,

насколько меньше памяти ЭВМ потребуется для запоминания ненулевых коэффи-

циентов в уравнениях в сравнении с тем случаем, когда пришлось бы запомнить

все коэффициенты уравнений, число которых равно

Отметим, что возможность использования симметрии коэффициентов урав-

нений и их “слабой заполненности” является важнейшим свойством, которое на-

до учитывать при сопоставлении различных методов расчета установившихся ре-

жимов.

Важной особенностью уравнений узловых напряжений является также про-

стота их составления – методика вычисления собственных и взаимных проводи-

мостей проста. Обычно в качестве исходных данных для расчетов установившихся

режимов ЭЭС задают сопротивления продольных ветвей (линий электропередачи,

трансформаторов и др.), проводимости на землю (линий электропередачи, реакто-

ров, трансформаторов), а также топологию схемы (схему соединений). Топология

схемы, как правило, отражается номерами узлов, соединенных ветвями. Собст-

венные и взаимные проводимости узлов рассчитываются на ЭВМ. Такой расчет

очень прост, так как выполняется в соответствии с выражениями (1.29) и (1.30).

Следует также отметить, что рассчитанные узловые напряжения позволяют

достаточно легко определить все остальные параметры режима ЭЭС.

Отмеченные выше особенности уравнений узловых напряжений обусловили

их широкое применение при расчетах установившихся режимов ЭЭС.

1.7. Уравнения контурных токов

Рассмотренные уравнения узловых напряжений основывались на использо-

вании первого закона Кирхгофа и закона Ома. Их применение позволяет значи-

тельно понизить порядок решаемой системы уравнений по сравнению с обобщен-

ными уравнениями состояния, поскольку количество узлов всегда меньше количе-

ства ветвей, особенно в сложных схемах.

Другим методом, дающим возможность понижения порядка решаемой сис-

темы уравнений, является метод контурных токов, основанный на использовании

второго закона Кирхгофа и закона Ома. При расчете режимов сети с помощью

этого метода считают, что в каждом независимом контуре протекает свой контур-

ный ток. При этом действительные токи ветвей, являющихся общими для двух

или более контуров, представляются в виде алгебраической суммы соответст-

вующих контурных токов, а токи в ветвях, входящих только в один контур, при-

равниваются соответствующим контурным токам с учетом выбранных положи-

тельных направлений токов ветви и контурного.

Введение этих контурных токов позволяет уменьшить число переменных в

системе уравнений состояния, так как число независимых контуров значительно

меньше числа ветвей.

Уравнения контурных токов можно получить на основании второго закона

Кирхгофа, если токи в ветвях выразить через контурные.

Рис.1.11. Схема замещения сети

Для схемы, изображенной на рис. 1.11, при принятых положительных на-

правлениях токов в ветвях и направлениях обхода контуров по второму закону

Кирхгофа можно записать 2 независимых уравнения:

.EIzIz

EIzIz

23322

13311

(1.38)

Уравнения (1.38) непосредственно решить нельзя, так как количество пере-

менных больше количества уравнений.

Выполним замену переменных в уравнениях (1.38). Для этого введем пред-

положение, что независимые контуры обтекаются некоторыми условными кон-

турными токами

1к

I и

2к

I , которые обладают таким свойством, что ток каждой

ветви может быть получен как алгебраическая сумма контурных токов, проте-

кающих по этой ветви. Тогда с учетом выбранных положительных направлений

токов ветвей и контурных токов для схемы рис.1.11 можно записать:

.III

кк

213

+-=

Тогда уравнения (1.38) можно записать в следующем виде:

(

)

( )

.EIIzIz

EIIzIz

ккк

221322

121311

=-×-

(1.39)

Сгруппируем подобные члены уравнений (1.39) относительно неизвестных

и введем следующие обозначения:

,EE

zzz

312

3222

3111

где

2211

z,z собственные сопротивления независимых контуров;

z взаимные

сопротивления контуров;

21 кк

Е,E контурные ЭДС.

С учетом принятых обозначений уравнения (1.39) примут следующий вид: