Васюра Ю.Ф. Математические методы расчета установившихся режимов работы электроэнергетических сетей

Подождите немного. Документ загружается.

Таким образом, для графа сети, изображенного на рисунке 2.4, первую мат-

рицу инциденций можно записать в следующем виде:

Каждая строка матрицы

М показывает, какие ветви соединены с данным узлом,

а также их направление по отношению к данному узлу. Каждый столбец матрицы

М показывает, какие узлы являются начальной и конечной вершинами соответ-

ствующей ветви. В каждом столбце матрицы

М может быть только одна поло-

жительная и одна отрицательная единица, а остальные элементы столбца равны

нулю. Поэтому при сложении всех строк матрицы

М по столбцам получается

нулевая строка:

(2.22)

Из (2.22) следует, что определитель матрицы

М равен нулю.

Поскольку матрица

М отражает все связи ветвей с узлами, то с ее помо-

щью можно записать уравнение первого закона Кирхгофа в матричном виде:

ув

M , (2.23)

где

I матрица-столбец неизвестных токов ветвей,

I матрица-столбец задающих токов узлов.

Следует отметить, что уравнения, записанные в соответствии с (2.23) для

всех узлов, не являются независимыми.

Для получения матрицы соединений, отвечающей системе независимых

уравнений, из матрицы

М следует исключить строку, соответствующую балан-

сирующему узлу. В связи с этим балансирующему узлу удобно присвоить послед-

ний номер.

Принимая для схемы, изображенной на рисунке 2.4, в качестве баланси-

рующего узел № 6, матрицу

, отвечающую системе независимых уравнений, а

также матрицу-строку

М , отвечающую балансирующему узлу, запишем в виде:

44444 344444 21

7654321

0001001

1-000000

11-1-0000

0001-100

00101-1-0

0100011-

узлы

ветви

1000000

1110000

0001100

0010110

0100011

М ;

[

]

0001001

М .

Тогда система независимых уравнений первого закона Кирхгофа примет следую-

щий вид:

ув

M . (2.24)

Таким образом, матрицу

М можно представить в виде двух блоков:

М .

Используя запись условия (2.22) через матрицы, разделенные на блоки, по-

лучим:

[]

1n , (2.25)

откуда следует, что матрица-строка

М , соответствующая в матрице

М балан-

сирующему узлу, может быть получена суммированием прочих строк по столбцам

и изменением знаков элементов суммарной матрицы на обратные:

МnМ

. (2.26)

Кроме того, из выражения (2.26) следует, что для практических расчетов доста-

точно воспользоваться матрицей

, так как по ней может быть восстановлена

матрица

М , а, следовательно, и вся схема:

×-

Мn

. (2.27)

Количество строк в матрице

соответствует количеству независимых уз-

лов, количество столбцов – количеству ветвей, т.е. в общем случае матрица

прямоугольная.

Для разомкнутой схемы, в том числе и для дерева графа, матрица

- квад-

ратная. Ее определитель равен +1 или –1, и она имеет обратную матрицу, элемен-

тами которой также являются 1; -1; 0.

В отличие от матрицы

М , матрица

в каждом столбце может содержать

как два, так и один значащий элемент. Последнее означает, что ветвь, соответст-

вующая столбцу с одним значащим элементом, одной из вершин соединена с ба-

лансирующим узлом.

Матрица

может быть представлена в виде двух блоков, отвечающих де-

реву (

М ) и хордам (

М ) графа. Для этого необходимо вначале пронумеровать

ветви дерева, а затем хорды, например, как показано на рис.2.2.

В этом случае для направленного графа, изображенного на рис.2.2, первая

матрица инциденций будет иметь вид:

[ ]

434214434421

ММ

МММ

000

011

101

111

100

001

Составление первой матрицы инциденций

легко формализуется с помо-

щью вычислительной техники. Обычно это выполняется простым перебором за-

данных ветвей схемы, т.к. схема задается именно ветвями, либо непосредственно

схемой замещения какого-либо элемента, либо его части. Ветвь задается с запи-

сью всех параметров, отвечающих графу схемы: номер ветви, номер начального

узла, номер конечного узла, активное сопротивление, реактивное сопротивление,

модуль ЭДС, фаза ЭДС.

При таком задании ветвей схемы, организовав цикл для анализа присоеди-

нений ветвей к узлам, можно легко составить матрицу

, используя только логи-

ческие операции.

Матрица М может быть применена также для определения падений напря-

жений на ветвях схемы

U .

Обозначим столбец напряжений всех узлов схемы (узловых напряжений) как

{

}

,…,n. По этим напряжениям с помощью матрицы

M можно опре-

делить падения напряжений на ветвях схемы. Если матрицу

M транспонировать,

то каждая строка матрицы

M будет содержать положительную единицу в столб-

це, соответствующем начальной вершине, и отрицательную единицу в столбце, со-

ответствующем конечной вершине. То есть при умножении матрицы

M на мат-

рицу-столбец напряжений узлов

U справа для каждой ветви схемы получим раз-

ность напряжений (или потенциалов) между ее начальной и конечной вершинами,

т.е. падение напряжений на этой ветви:

UMU

. (2.28)

Здесь матрица

U записана для всех узлов схемы, включая балансирующий.

Часто узловые напряжения целесообразно определять относительно балан-

сирующего узла, т.е. как падения напряжения от каждого из независимых узлов

схемы до балансирующего. Эти значения отличаются от напряжений нейтрали на

одну и ту же величину – напряжение балансирующего узла

U :

=×-

nUU

, (2.29)

где

- единичный столбец (при этом балансирующий узел предполагается по-

следним по номеру, т.е.

);

{

}

U , i =1, …, n-1 - определяет напряжения узлов относительно ба-

лансирующего.

Тогда для падений напряжений на ветвях можно записать:

[ ]

×=

MMU

бttв

. (2.30)

После перемножения получим:

бt

MUMU

или

UMU

, (2.31)

где

Для напряжений узлов можно записать:

UUU

,…, n - 1

U ×+

S б

2.4.2. Матрица соединений ветвей графа в независимых контурах

(вторая матрица инциденции)

Вторая матрица инциденций

(матрица контуров) служит для обобщенного

аналитического представления соединений ветвей схемы в независимые замкну-

тые контуры. Принцип ее составления может быть получен из анализа общей фор-

мы записи уравнений по второму закону Кирхгофа.

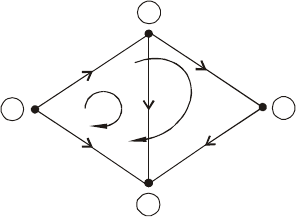
Для примера рассмотрим граф, изображенный на рис.2.5.

Рис. 2.5

Запишем уравнения по второму закону Кирхгофа, выбрав произвольно на-

правления обхода контуров

010111

001101

54321

=×+×+×-×+×

UUUUU

Представим индексы в матричной форме:

444344421

ветви

10111

01101

N независимые контуры

В матричном виде для каждого контура можно записать:

0 . (2.32)

Таким образом, записывая формально уравнения второго закона Кирхгофа

по уравнению (2.32), где i изменяется от 1 до n, n - число ветвей контура, можно

отметить, что

m принимает одно из трех значений: +1, если ветвь входит в неза-

висимый замкнутый контур и совпадает с направлением обхода; -1, если ветвь

входит в независимый замкнутый контур, но не совпадает с направлением его об-

хода; 0, если ветвь не входит в рассматриваемый контур.

Если эти индексы записать для всех независимых контуров и представить в

табличной форме, то получим матрицу, столбцы которой будут отвечать ветвям, а

строки – контурам. На пересечении столбца и строки записываются индексы при-

надлежности ветви тому или иному контуру. Эта матрица получила название мат-

рицы контуров. Каждая строка матрицы

показывает, какие ветви входят в состав

соответствующего независимого замкнутого контура и с каким направлением от-

носительно направления контура. Каждый столбец матрицы

показывает, в со-

став каких независимых замкнутых контуров входит данная ветвь и совпадает ли

ее направление с направлением обхода этих контуров.

Порядок составления матрицы

следующий: после обозначения и придания

направления всем ветвям выбираются независимые замкнутые контуры схемы,

выбираются направления обхода контуров. Затем строится матрица

, в которой

отражаются индексы принадлежности каждой ветви каждому независимому кон-

туру.

Матрица

имеет столько строк, сколько столбцов имеет подматрица

M .

Оба числа равны числу хорд, или, что то же, числу независимых контуров в схеме.

Вид матрицы

зависит от выбора независимых замкнутых контуров и принятых

направлений их обхода. При одной и той же нумерации узлов и ветвей в зависимо-

сти от выбора независимых контуров получаются различные матрицы, т.е. одному

и тому же графу сети может соответствовать несколько матриц

В общем случае матрица

прямоугольная, т.е. не имеет обратной. Если в

схеме имеются ветви, не входящие в замкнутый контур, то они не отображаются в

матрице

, следовательно, по ней невозможно восстановить исходную схему (в

отличие от матрицы

Матрицу

целесообразно разделить на блоки (как и матрицу

) так, чтобы

одна из подматриц получилась квадратной. Такое разделение на блоки удобно

производить в соответствии с делением схемы на дерево и хорды:

][

NNN

. (2.33)

При нумерации ветвей схемы целесообразно вначале нумеровать ветви дере-

ва, а затем хорды. При этом каждой ветви дерева дается номер ее конечного узла, а

хорды нумеруются в той же последовательности, в какой пронумерованы соответ-

ствующие независимые контуры. Каждый из контуров замыкается одной хордой,

т.е. каждая хорда входит только в один контур. Кроме того, направления обхода

указанных независимых контуров должны совпадать с направлениями соответст-

вующих хорд. При этом подматрица

N получается квадратной и единичной.

Рассмотренные контуры называют базисными. Они взаимно независимы, так

как в каждый из них входит одна ветвь (хорда), не входящая ни в какой другой

контур.

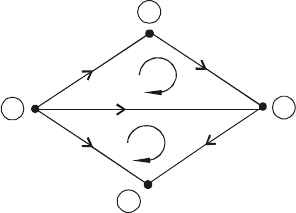
Для примера составим матрицу

для графа сети, изображенного на рис.

2.6, используя правило выбора базисных контуров.

Рис.2.6. К правилу выбора базисных контуров

В этом случае матрица контуров будет иметь вид:

32143421

110

011

Матрица

позволяет получить матричную запись уравнений второго закона

Кирхгофа:

UN , (2.34)

где

U столбец падений напряжений на ветвях схемы.

Действительно, из всех падений напряжений будут алгебраически суммиро-

ваться только падения напряжения на тех ветвях, которые входят в данный незави-

симый контур.

Формализованное составление матрицы

по сравнению с первой матрицей

инциденций

с точки зрения реализации на ЭВМ выполняется более сложно, по-

скольку необходимо выделить независимые контуры, а эта операция неоднознач-

на.

Однако, если учесть, что первая матрица инциденций

содержит информа-

цию о всей схеме, то можно предположить, что по ней может быть получена и

вторая матрица инциденций

. Эта операция действительно осуществима, если

использовать понятия дерева и базисной системы хорд, замыкающих базисные

контуры.

Из выражений (2.31) и (2.34) следует, что

UMN

(2.35)

Это выражение справедливо в общем случае, т.е. при любых

U . Тогда

NM . (2.36)

Это условие относится к топологическим свойствам графа и связывает пер-

вую и вторую матрицу инциденций.

Однако, для получения матрицы

в приведенном виде его использовать

нельзя. Воспользуемся представлением схемы в виде дерева и хорд. Тогда каждая

из матриц может быть записана в виде блоков, отвечающих дереву и хордам.

[ ]

NN ; (2.37)

После перемножения матриц получим матричное уравнение

bbaa tt

MNMN ; (2.38)

или

tt bbaa

MNMN . (2.39)

Поскольку

M квадратная, неособенная и имеет обратную

М , то умно-

жая (1.80) на

М справа, для подматрицы дерева можно записать:

abba

-= MMNN ; (2.40)

Это выражение позволяет получить подматрицу дерева, если имеется под-

матрица хорд. Подматрица хорд является единичной диагональной матрицей, если

соблюдать правило выбора базисных контуров, рассмотренное ранее.

Тогда из (2.40) можно получить

aba

MMN

. (2.41)

Таким образом, выражение для матрицы

получим в следующем виде:

[

]

1NN

. (2.42)

2.5. Независимые параметры режима электрической цепи

При расчете режима сети с использованием законов Кирхгофа количество

уравнений получается наибольшим, т.к. неизвестными являются токи в ветвях

схемы. Между тем, использование методов узловых напряжений и контурных то-

ков позволяет понизить количество решаемых уравнений.

Возможность понижения порядка системы уравнений связана с тем обстоя-

тельством, что не все напряжения и токи электрической цепи являются независи-

мыми.

Для определения независимых токов воспользуемся матричной записью

первого закона Кирхгофа (2.24):

ув

M .

Будем считать, что в схеме выделено дерево и базисные хорды, замыкаю-

щие независимые базисные контуры. Тогда с учетом сказанного, можно записать:

[ ]

MM . (2.43)

Выполнив операцию умножения, получим следующее матричное уравнение:

увв

III

bbaa

МM . (2.44)

Перенося второе слагаемое в правую часть и умножая почленно обе части на

M ,

получим:

(

)

bbaa

вув

III MM -×=

-1

. (2.45)

Раскрывая скобки, получим:

bbaaa

вув

III MMM

11 --

-×= . (2.46)

Из выражений (2.45), (2.46) следует, что в любой схеме достаточно опреде-

лить токи хорд, чтобы на основании их можно было определить и токи, относя-

щиеся к ветвям дерева.

Для получения более общего выражения токов во всех ветвях через токи в

хордах будем использовать выражение (2.41):

aba

MMN .

Тогда для транспонированной матрицы можно записать:

baa

MMN ×-=

. (2.47)

Подставляя (2.47) в (2.46), получим:

baaa

вtув

III NМ +=

-1

. (2.48)

Матрицу токов в ветвях представим в виде блоков

вв

II , :

baa

вtу

NМ

. (2.49)

После преобразования получим:

вув

III ×

+×

. (2.50)

Это уравнение связывает токи ветвей схемы с токами независимых контуров.

Учитывая, что в схеме выбраны базисные контуры, можно записать выра-

жение, определяющее токи в ветвях:

вtув

III N

+×

. (2.51)

Это означает, что при известной матрице токов

I можно определить токи во

всех ветвях.

Для определения независимых напряжений электрической цепи воспользу-

емся выражением (2.37), связывающим падения напряжения на ветвях схемы и

напряжения узлов относительно базисного узла

UМU

tв

Решение обратной задачи, т.е. непосредственное нахождение напряжений

узлов относительно базисного при известных падениях напряжений на ветвях

схемы в общем случае невозможно, т.к. матрицы

М для замкнутых схем яв-

ляются прямоугольными и не имеют обратных.

Математически это означает, что система уравнений (2.31) не является сис-

темой независимых уравнений и не может быть решена без дополнительных пре-

образований.

Физически это означает, что не все падения напряжений на ветвях являются

независимыми. Действительно, анализируя второй закон Кирхгофа нетрудно ус-

тановить, что падение напряжения на любой ветви, входящей в замкнутый контур,

равно алгебраической сумме падений напряжения на остальных ветвях данного

контура, взятой с обратным знаком.

Преобразуем рассматриваемую систему уравнений, используя понятия де-

рева и хорд графа. Примем такой порядок нумерации ветвей, чтобы сначала были

обозначены ветви дерева, а затем хорды.

Используя запись матрицы в виде блоков, относящихся к дереву и хордам,

несложно преобразовать (2.31) к виду:

. (2.52)

Уравнение (2.52) эквивалентно двум матричным уравнениям:

UМU

tв

, (2.53)

UМU

tв

. (2.54)

Умножив обе части (2.53) на

слева и подставляя выражения для

U в (2.54),

получим падения напряжения на хордах схемы через падения напряжения на вет-

вях дерева:

aabb

вttв

UMMU ××=

. (2.55)

Выражение (2.55) отражает принцип независимости падений напряжения на

ветвях дерева схемы, расчет которых дает возможность определить падения на-

пряжения на всех остальных ветвях (хордах), а также напряжения в узлах схемы

относительно базисного

U и, наконец, напряжения в узлах относительно любой

точки, лежащей вне схемы, если известно напряжение базисного узла

U относи-

тельно этой точки.