Тюрев В.В. Гиперзвуковые течения газа
Подождите немного. Документ загружается.

81
7
6
5
4
3
2
1
60
°
30
°
20
°
10
°
98
7
654
321
0
2
k
M
xa
C
10
90
°
9
8
Рис. 33. Зависимость коэффициента сопротивления
пластины от числа Маха при свободно-молекулярном
течении газа
15.2. Определение сил, действующих на круговой цилиндр
при свободно-молекулярном обтекании
Аэродинамические силы при свободно-молекулярном обтекании
можно рассчитать и для тел более сложной формы, чем плоские пла-
стины, но при этом расчет целесообразно проделать для передней и
тыльной сторон тела порознь, пользуясь соответствующими выраже-
ниями (78) и (79) или (80) и (81) для нормальных и тангенциальных на-
пряжений.
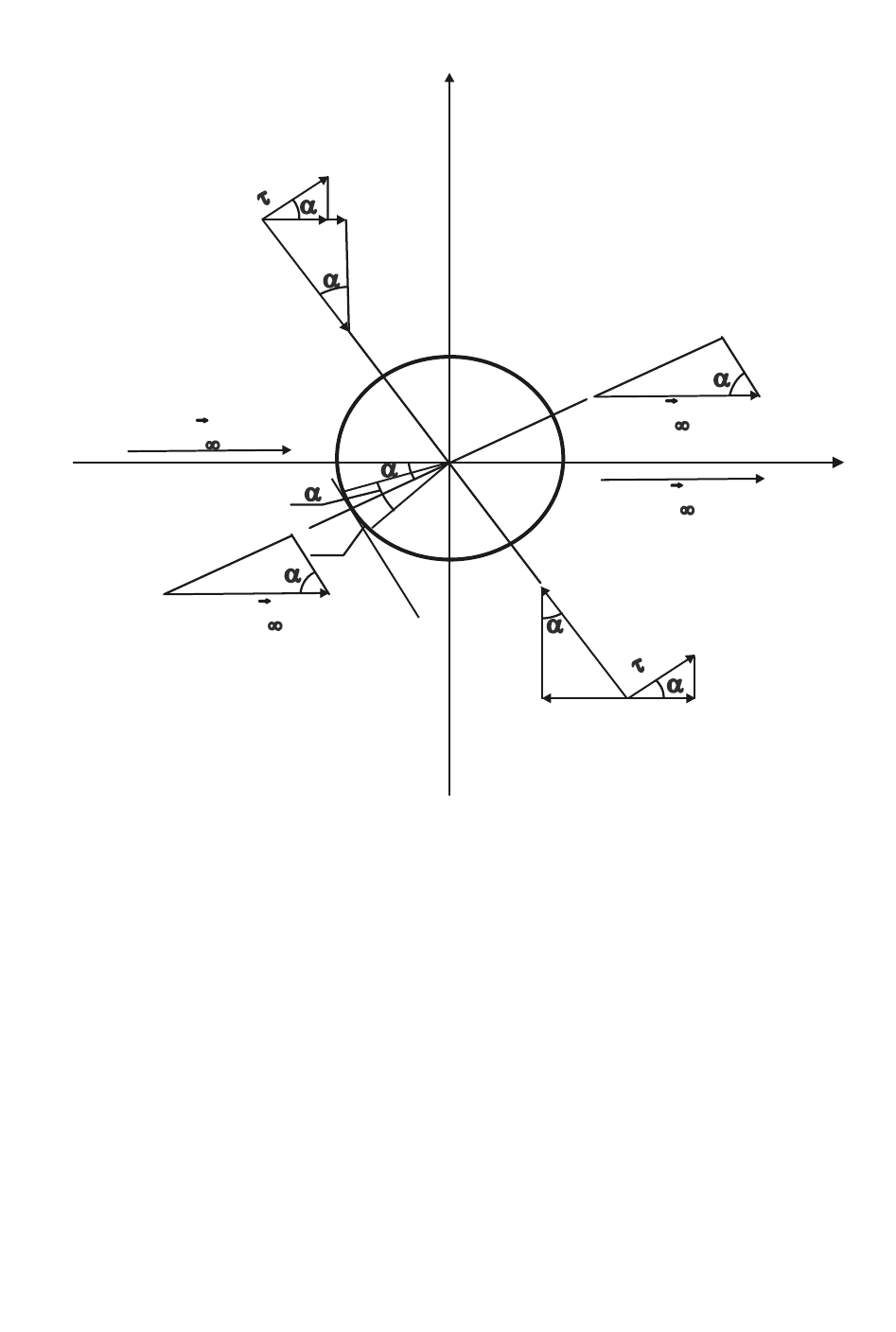
Выполним расчет аэродинамических сил при свободно-молекуляр-
ном поперечном обтекании кругового цилиндра бесконечной длины.
На рис. 34 показана элементарная аэродинамическая сила, дей-
ствующая на выделенный элемент площади dS . Радиус цилиндра
обозначен через R , угол между нормалью к элементу
dS
и скоростью
82
d
y
x
d
S
з
d
S
п
d
S
p
з
d
S
p
п
V
V
V
V
R
dS
Рис. 34. К определению проекций сил давления и трения на
направление потока при поперечном обтекании цилиндра
набегающего потока – через
ϕ
, а угол между касательной к элементу
dS и скоростью набегающего потока – через α .
Площадь выделенного элемента поверхности равна
α= RddS
.
Проекция аэродинамической силы, приложенной к элементарной
площадке dS , на направление невозмущенного потока (вклад пло-
щадки
dS
в силу сопротивления пластины) в соответствии с рис. 34
равна
(
)
ατ+α= cossinpdX
ппп
,
(
)
ατ+α−= cossinpdX
ззз
. (85)
Проекция той же силы на перпендикуляр к направлению невоз-
мущённого потока записывается следующим образом:
83
(
)
ατ−α= sincospdY
ппп
,
(
)
ατ+α= sincospdY
ззз
. (86)
Проинтегрировав записанные выражения в пределах от
1
α (ниж-
ний край поверхности тела) до
2
α (верхний край), получим значения
силы лобового сопротивления X и подъемной силы Y , действующих
на заданный участок поверхности тела. В частном случае цилиндра
(рис. 34) подъемная сила отсутствует ( 0=Y ), а сила лобового сопро-
тивления может быть получена из формул (85) с помощью равенств
(78) и (79) для передней стороны цилиндра (единичной длины).
Составляющую коэффициента силы сопротивления, обусловлен-
ную обтеканием передней стороны цилиндра, обозначим через
xп
С и
определим по формуле
S
V
X
С
п
xп
2
2
∞∞
ρ
=
.
Следовательно, для данного коэффициента справедливо соотно-
шение
+
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
α+
π
=
α−
π
∞
∞
∞
∫
2
2
2
2
0
2
2
1
2
2
sin
kM
xп
esin
Mk
kM
С
αααα
π
dsin
Mk
erfsinsin
MkkM
⎪
⎭
⎪
⎬
⎫
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+++
∞∞∞
2
1
2
222
1
2
.
Для задней стороны цилиндра составляющую коэффициента силы
сопротивления обозначим через
xз
С и определим следующим обра-
зом:
S
V
X
С
з
xз
2
2
∞∞
ρ
=
.
Формула, по которой может быть вычислен введенный коэффици-
ент, получается аналогичным путем с помощью выражений (80) и
(81):
84
+
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
α−
π
=
α−
π
∞
∞
∞
∫
2
2
2
2
0
2
2
1
2
2
sin
kM
xз
esin
Mk
kM
С
α
⎪
⎭
⎪
⎬
⎫
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
α−α
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
α
π
+−−+
∞∞∞
dsin
Mk
erfsinsin
MkkM
2
1
2
222
1
2
.
Суммарный коэффициент сопротивления определяется как сумма
двух записанных коэффициентов:
xзxпx
ССС += .
Учитывая симметрию формул для коэффициентов
xп
С и
xз
С , вы-
ражение для коэффициента сопротивления
x
С можно получить в сле-
дующем виде:
+α
π
=
∫
π
α−
∞
∞
2
0
2
2
2
22
de
Mk
С
sin
kM
x
+α
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
α⋅α
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++
∫
π
∞
∞
2
0
2
2
2
2
dsin
Mk
erfsin
kM
∫
π
∞
α⋅α
π
+
2
0
2
2
dsin
Mk
. (87)
Для удобства дальнейших расчётов вводится обозначение
2
∞
=
Mk
s ,
тогда равенство (87) приобретает вид
+α
π
=
∫
π
α−
2
0
22
2
de
s
С
sins
x
()
+αα⋅α
⎟
⎠
⎞
⎜
⎝
⎛
++
∫
π
2
0
2
2
1
dsinserfsin
s
∫
π
α⋅α
π
2
0
2
dsin
s
. (88)
85
Значения интегралов, входящих в выражения (88), приведены в
работе [21], и они записываются следующим образом:
0
2
2
0
1
2
22
2
JedeF
s
sins
−
π
α−
π
=α=
∫
;
()
()
10
2
2
0
2
2
2
JJe
s
dsinserfsinF
s
+
π
=αα⋅α=
−
π
∫
;
∫
π
π
=α⋅α=
2
0
2
3
4
dsinF
.
Величины
0
J и
1
J , входящие в функции
1
F и
2
F , представляют
собой так называемые модифицированные функции Бесселя – соот-
ветственно порядка 0 и 1. Они вычисляются как значения соответст-
вующих интегралов:
∫
−
−
π
=
1
1
2
2
0
1
1
2
dx
x
e
J
x
s
,
∫
−
−
π
=
1
1
2
2
2
1
1
2
1
2
dxxesJ
x
s
.
Значения
()
sJ
0
и
()
sJ
1
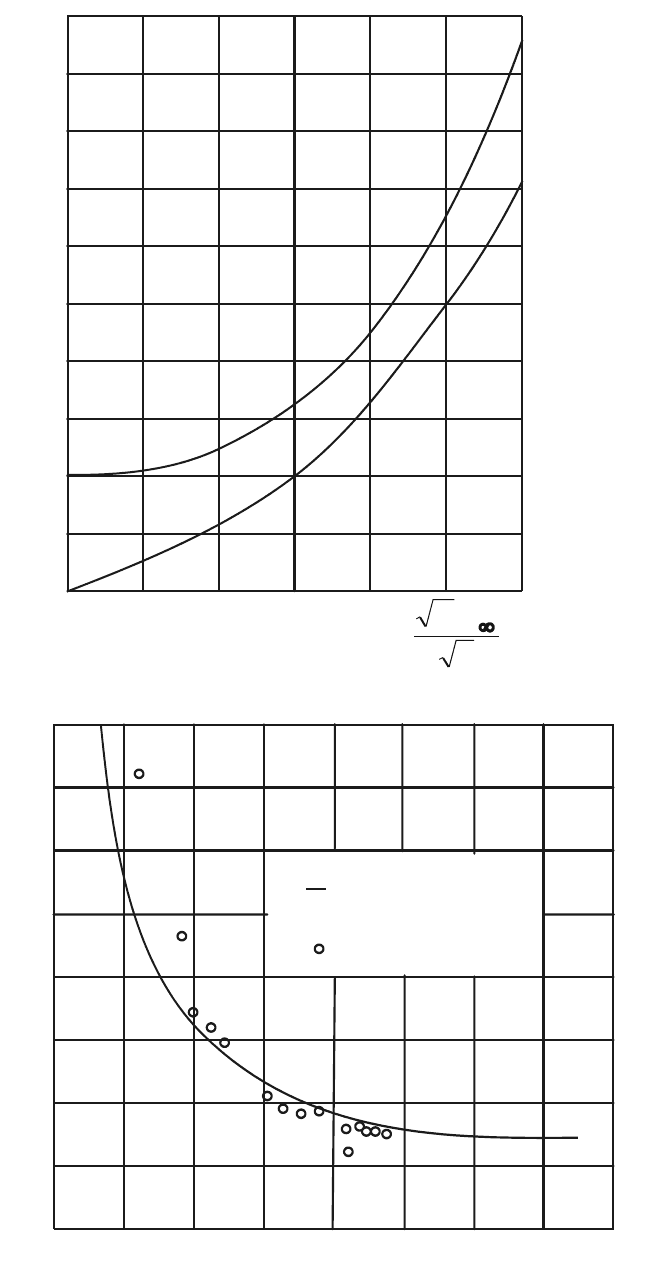
приведены на рис. 35.
Подставляя значения
1
F ,
2
F и
3
F в равенство (88), получим
окончательно:
()
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
π
+
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
++
π
=
−
42
1
10
2
0
2
1
2
JJsJe
s
С
s
x
.
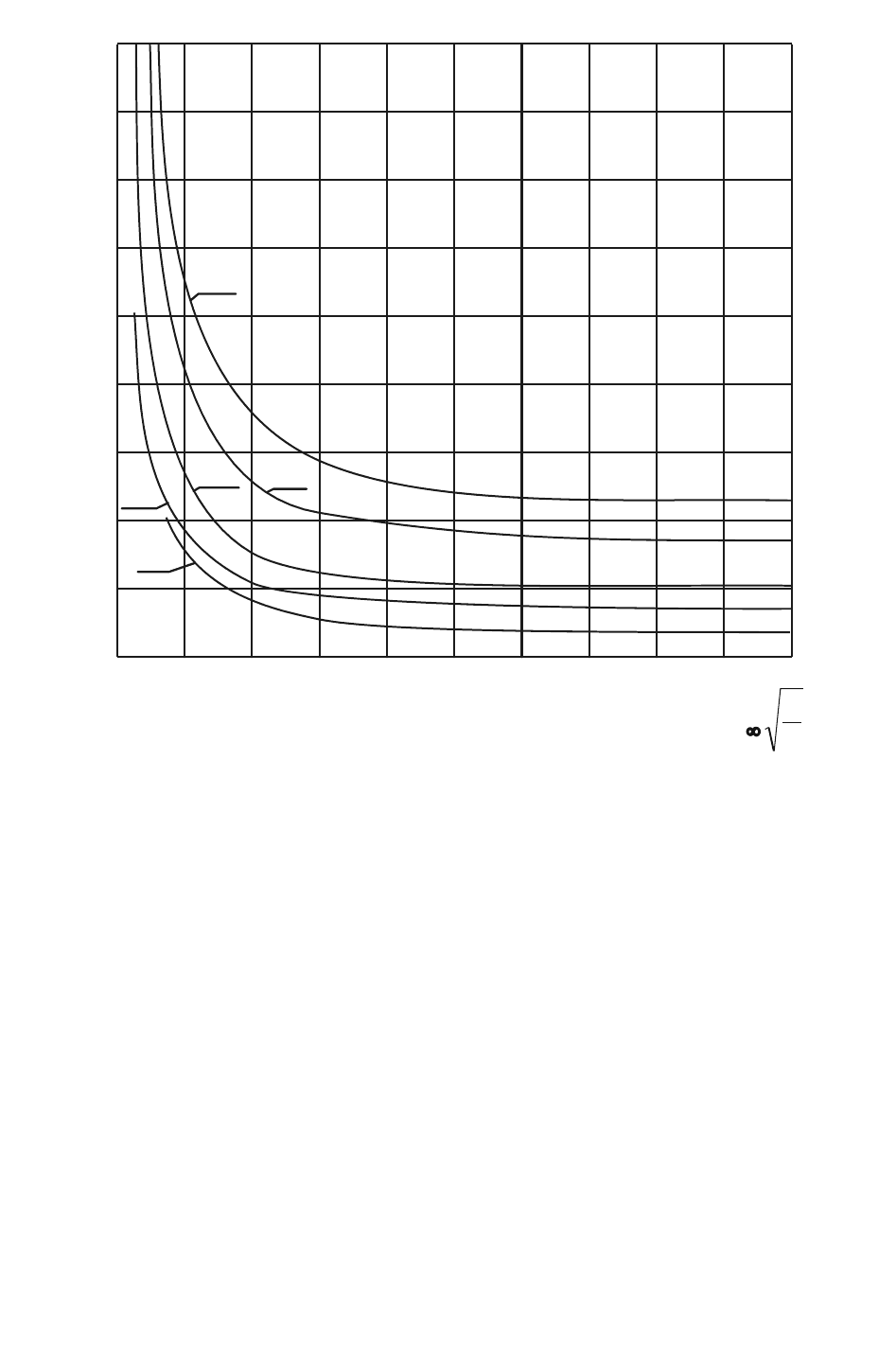
На рис. 36 показана рассчитанная по формуле (88) зависимость
коэффициента сопротивления цилиндра от числа
2
∞
=
Mk
s
при сво-
бодно-молекулярном его обтекании гелием. Для сравнения на этом
графике приведены также экспериментальные точки, полученные
Штальером, Гудвиным и Кригером в аэродинамической трубе NACA.
86
2
=
Mk
s
5
4
3
2
1
0
1
J
0
J
3
2
1
1
J
0
J
тЭксперимен
Теория
s
С
x
.23
.82
.42
.02.61.21
.
8
0
.4
0
16
14
12
10
8
6
4
2
0
Рис. 35.
Модифицированные
функции Бесселя нулевого
и первого порядков
Рис. 36.
Зависимость
коэффициента
сопротивления от
параметра
s
при
поперечном обте-
кании цилиндра
При отыскании аэродинамических сил, возникающих при свобод-
но-молекулярном обтекании пластины и цилиндра, предполагалось,
87
что температура поверхности тела равна температуре невозмущённо-
го набегающего потока. В этом случае все расчётные формулы значи-
тельно упрощались. Для определения истинной температуры на по-
верхности тела необходимо воспользоваться методикой, изложенной
при рассмотрении теплового пограничного слоя.
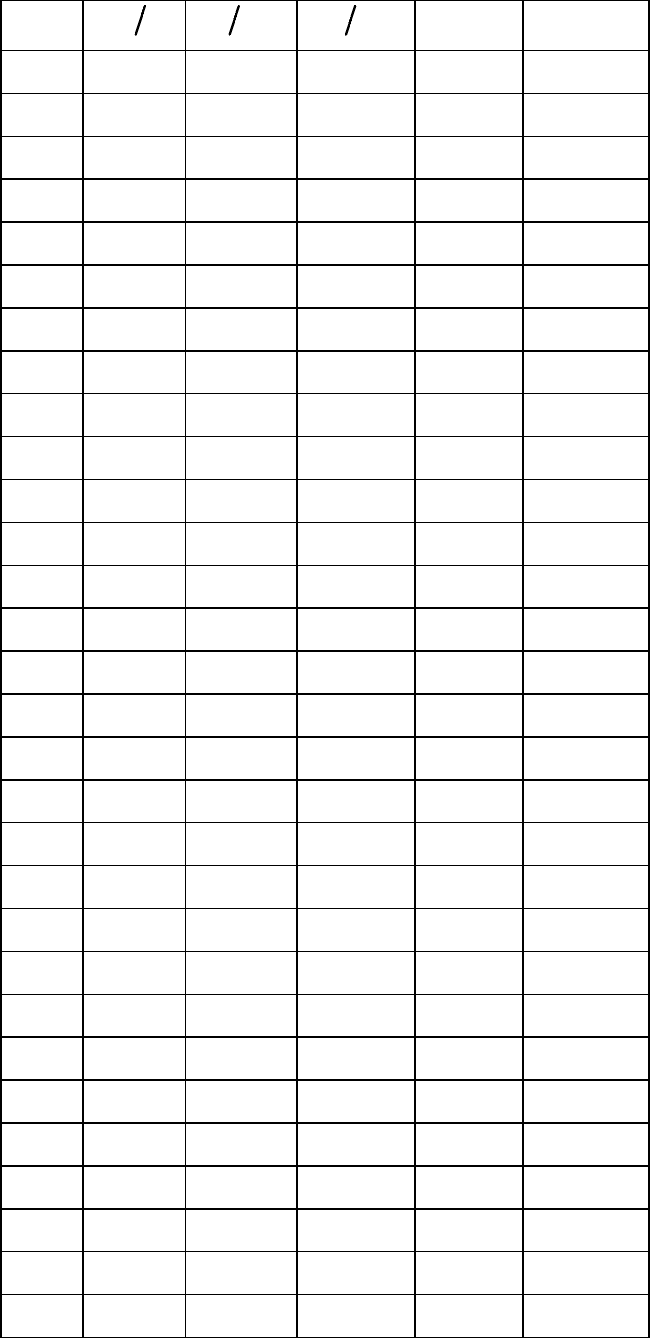
Таблица 3
Газодинамические функции
λ
0
TT
0
pp
0
ρρ
q
M
0,00 1 1 1 0 0
0,01 1 0,9999 0,9999 0,0158 0,0091
0,02 0,9999 0,9998 0,999 0,0316 0,0183
0,03 0,9999 0,9995 0,9997 0,0473 0,0274
0,04 0,9997 0,9990 0,9993 0,0631 0,0356
0,05 0,9996 0,9986 0,9990 0,0789 0,0457
0,06 0,9994 0,9979 0,3385 0,0945 0,0548
0,07 0,9992 0,997I 0,9970 0,1102 0,0639
0,08 0,9989 0,9963 0,9974 0,1259 0,0731
0,09 0,9937 0,9953 0,9967 0,1415 0,0822
0,10 0,9983 0,9942 0,9959 0,1571 0,0914
0,11 0,9980 0,9929 0.9949 0,1726 0,1005
0,12 0,9976 0,9916 0,9940 0,1832 0,1097
0,13 0,9972 0,9901 0,9929 0,2036 0,1190
0,14 0,9967 0,9886 0,8818 0,2190 0,1280
0,15 0,9963 0,9870 0,9907 0,2344 0,1372
0,16 0,9957 0,9851 0,9893 0,2497 0,1460
0,17 0,9952 0,9832 0,9880 0,2649 0,1560
0,18 0,9946 0,9812 0,9866 0,2801 0,1650
0,19 0,9940 0,9791 0,9850 0,2952 0,1740
0,20 0,9933 0,9768 0,9834 0,3102 6,1830
0,21 0,9927 0,9745 0,9817 0,3253 0,1920
0,22 0,9919 0,9720 0,9799 0,3401 0,2020
0,23 0,9912 0,9695 0,9781 0,3549 0,2109
0,24 0,9904 0,9668 0,9762 0,3696 0,2202
0,25 O.S896 0,9640 0,9742 0,3842 0,2290
88
Продолжение табл. 3
λ
0
TT
0
pp
0
ρρ
q
M
0,26 0,9887 0,9611 0,9721 0,3987 0,2387
0,27 0,9879 0,9581 0,9699 0,4131 0,2480
0,28 0,9869 0,9550 0,9677 0,4274 0,2573
0,29 0,9860 0,9518 0,9653 0, 4416 0,2470
0,30 0,9850 0,9485 0,9630 0,4557 0,270
0,31 0,9840 0,9451 0,9605 0,4697 0,2850
0,32 0,9829 0,9415 0,9579 0,4835 0,2947
0,33 0„9819 0,9379 0,9552 0,4972 0,3040
0,34 0,9807 0,9342 0,9525 0,5109 0,3134
0,35 0,9798 0,9303 0,9497 0,5243 0,3228
0,36 0,9784 0,9265 0,9469 0,5377 0,3322
0,37 0,9772 0,9224 0,9439 0,5509 0,3417
0,38 0,9759 0,9183 0,9409 0.5S40 0,3511
0,39 0,9747 0,9141 0,9378 0,5769 0,3605
0,40 0
s
9733 0,9097 0,9346 0,5897 0,3701
0,41 0,9720 0,9053 0,9314 0,6024 0,3796
0,42 0,9707 0,9008 0,9284 0,6149 0,3892
0,43 0,9692 0,8962 0,9247 0,6272 0,3987
0,44 0,9677 0,8915 0,9212 0,6394 0,4083
0,45 0,9663 0,8968 0,9178 0,6515 6,4179
0,46 0,9646 0,6819 0,9142 0,5833 0,4275
0,47 0,9632 0,8770 0,9105 0,6750 0,4372
0,48 0,9616 0,8719 0,9067 0,6885 0,4458
0,49 0,9600 0,8668 0,9029 0,6970 0,4585
0,50 0,9583 0,8616 0,8991 0,7091 0,1663
0,51 0,9567 0,8563 0,8951 0,7201 0,4760
0,52 6,9549 0,8509 0,8911 0,7309 0,4858
0,53 0,9532 0,8455 0,8871 0,7416 0,4956
0,54 0,9514 0,8400 0,8629 0,7520 0,5054
0,55 0.9445 0,8344 0,8787 0,7623 0,5152
89
Продолжение табл. 3
λ
0
TT
0
pp
0
ρρ
q
M
0,56 0,9477 0,8287 0,8744 0,7724 0
:
5252
0,57 0,9459 0,8230 0,8701 0,7623 0,5350
0,58 0,9439 0,8172 0,8657 0,7920 0,5450
0,59 0,9420 0,8112 0,86I2 0,80I5 0,5549
0,60 0 9400 0
s
8053 0,8567 0,8109 0,5649
0,61 0,9380 0,7992 0,852I 0,8198 0,5750
0,62 0,9359 0,7932 0
,
8475 0,8288 0,5850
0,63 0,9339 0,7870 0,8428 0,8375 0,5951
0,64 0,9317 0,7808 0,8308 0,8459 0,6053
0,65 0,9296 0,7745 0,8332 0,8543 0,6154
0,63 0,9274 0,7681 0,8283 0,8623 0,6256
0,67 0,9252 0,76I7 0,8233 0,8701 0,6359
0.68 0,9229 0,7653 0,8183 0,8778 0,6461
0,69 0,9207 0,7488 0,8133 0,8852 0,6565
0,70 0,9I83 0
,
7422 0,8062 0,8924 0,6668
0,71 0,9I60 0,7356 0,8030 0,8993 0,8772
0,72 0,9136 0,7289 0,7978 0,9081 0,6876
0,73 0,9112 0,7221 0,7925 0,9126 0,6981
0,74 0,9087 0,7154 0,7872 0,9188 0,7086
0,75 0,9063 0,7086 0,7819 0,9250 0,7192
0,76 0,9037 0,7017 0,7764 0,9308 0,7298
0,77 0,9012 0,6948 0,7710 0,9364 0,7404
0,78 0,8986 0,6878 0,7655 0,9418 0,7511
0,79 0,8960 0,6809 0,759S 0,3469 0,7619
0,80 0,8933 0,6736 0,7543 0,9518 0,7727
0,81 0,8907 0,6S68 0,7486 0,9565 0,7835
0,82 0,6879 0,6597 0,7429 0,9610 0,7944
0,83 0,8852 0,6526 0,7372 0,9652 0,8053
0,84 0,8824 0,6454 0,73I4 0,969I 0,8163
0,85 0,8796 0,6382 0,7256 0,9729 0,8274

90
Продолжение табл. 3
λ
0
TT
0
pp
0
ρρ
q
M
0,86 0,87S7 0,63I0 0,7197 0,9764 0,8383
0,87 0,8739 0,6238 0,7138 0,9796 0,8496
0,88 0,8709 0,8165 0,7079 0,9826 0,8606
0,89 0,8680 0,6092 0,7919 0,9854 0,8721
0,90 0,8650 0,6019 0,6959 0,9879 0,8833
0,91 0,8620 0,5946 0,6998 0,9902 0,8947
0,92 0,8589 0,5873 0,6838 0,9323 0,9062
0,93 0,8559 0,5800 0,6776 0,9941 0,9177
0,34 0,3627 0,5726 0,6715 0,9957 0,9292
0,95 0,8496 0,5683 0,6653 0,8070 0,9409
0,96 0,8464 0,5679 0,6591 0,9981 0,9526
0,97 0,8432 0,5506 0,6528 0,^389 0,9644
0,98 0,8399 0,5431 0,6466 0,9995 0,9761
0,99 0,8367 0,5357 0,6403 0,9999 0,98 0
1,00 0,8333 0,5283 0,6340 1,0000 1,0000
1,01 0,8300 0,5209 0,6276 0,9999 1,0120
1,02 0,8266 0,5135 0,6212 0,9995 1,0241
1,03 0,8232 0,5061 0,6148 0,9989 1,0363
1,04 0,8197 0,4987 0,6084 0,9980 1,0486
1,05 0,8163 0,4913 0,6019 0,9969 1,0609
1,06 0,8127 0,4840 0,5955 0,9957 1,0733
1,07 0,8092 0,4756 0,5890 0,9941 1,0858
1,08 0,8056 0,4693 0,5826 0,9924 1,0985
1,09 0,8020 0,4619 0,5760 0,9903 1,1111
1,10 0,7983 0,4546 0,5694 0,9880 1,1239
1,11 0,7947 0,4473 0,5629 0,9856 1,1367
1,12 0,7909 0,4400 0,5564 0,9829 1,1496
1,13 0,7872 0,4328 0,5498 0,9800 1,1627
1,14 0,7834 0,4255 0,5432 0,9768 1,1758
1,15 0,7796 0,4184 0,5366 0,9735 1,1890
