Тюрев В.В. Гиперзвуковые течения газа
Подождите немного. Документ загружается.

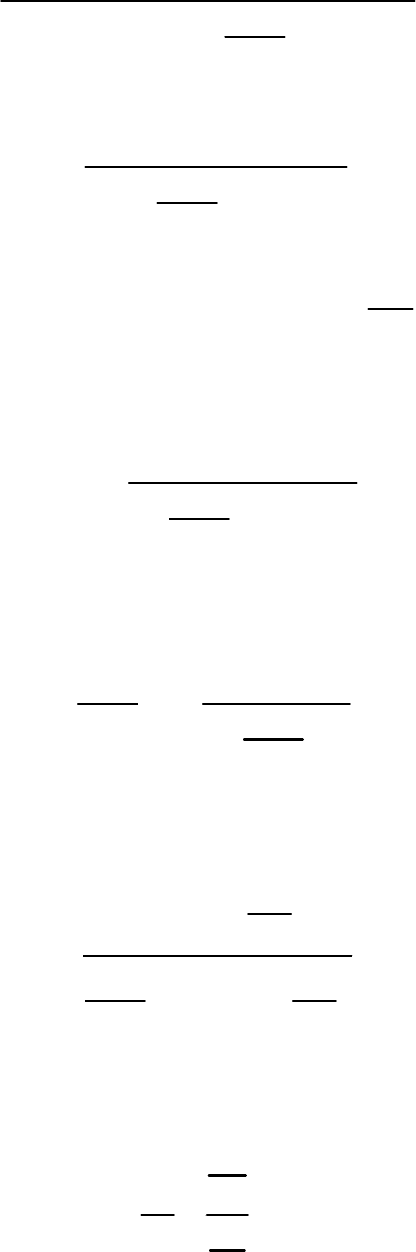
21
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
β
+
−
−+β
β= 1
1
1
22222
2
cosV
k
k
acosV
V
ctg
нкрн
н
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
β
+
−
β= 1
1
2
222
2
cosV
k
a
V
ctg
нкр
н
.
Введя относительную скорость
λ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=λ
кр
н
н
a
V
, это выражение
можно записать следующим образом:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
βλ
+
−
λ
β=ϖ 1
1
2
1
22
2
cos
k
ctgtg
н
н
.
Используя связь между относительной скоростью и числом Маха,
приведенную в работе [3]:
2
2
2
1
1
1
1
1
1
M
k
k
k
−
+
=λ
−
+
−
,
можно окончательно получить такое соотношение между углами
ϖ
и
β
:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β−
+
−β
β=ϖ
2
2
2
2
1
2
1
1
н
н
M
sin
k
M
sin
ctgtg
. (35)
Температуру за скачком уплотнения с помощью уравнения со-
стояния определяют по следующей формуле:
н
н
н
p
p
T
T
ρ
ρ
=
.
Воспользовавшись формулами (31) и (32), находим такое равен-
ство:

22
β
+
⎟
⎠
⎞
⎜
⎝
⎛
β
−
+
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−β
+
=
22
2222
2
1
2
1
1
1
1
1
2
sinM
k
sinM
k
k
k
sinM
k
k
T
T
н
нн
н
.
Для определения скорости звука запишем следующую
формулу:
нн
T
T
a
a
=
.
Проекции скорости возмущения
v
на оси
x
и
y
обозначены через
x
v и
y
v
. Указанные проекции определяются в соответствии с данными
рис. 6 и 7:
⎭
⎬
⎫
=
−=
.sin
,cos
ϖ
ϖ
Vv
VVv
y
нx
(36)
Связь между скоростями
V
и
н
V видна из соотношения
α=β=
τ
cosVcosVV
н
,
откуда следует, что
α
β
=
cos
cos
VV
н
.
Поэтому равенства (36) можно записать следующим образом:
⎪
⎪
⎭
⎪
⎪
⎬
⎫
ϖ
α
β
=
⎟
⎠
⎞
⎜
⎝
⎛
−
α
ϖβ
=
.sin
cos
cos
Vv
,
cos
coscos
Vv
нy
нx
1
(37)
Принимая во внимание, что справедливо равенство
(
)
ϖ−β=α coscos , для компонентов скорости возмущений получаем
такие значения:
()
ϖβ+ϖβ
ϖβ
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
ϖ−β
ϖβ
=
sinsincoscos
sinsin
V
cos
coscos
Vv
ннx
1
.
Это выражение перепишем следующим образом:
1
1
+ϖβ
−=
ctgctg
Vv
нx
.
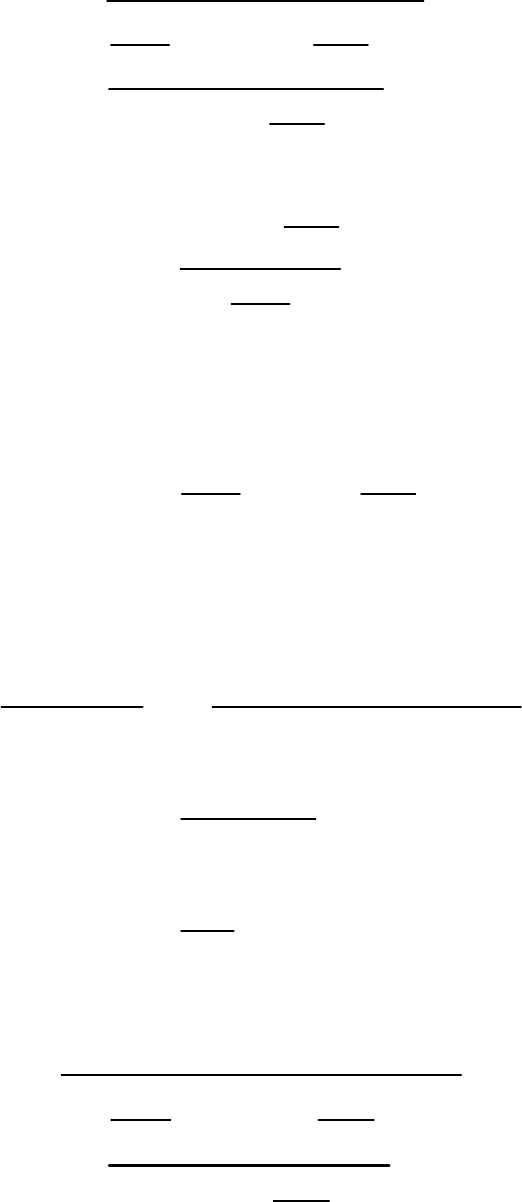
23
Используя формулу (35), полученное выражение преобразуем к
виду:
=
+
−β
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β−
+
−=
1
1
1
2
1
1
2
2
2
2
н
н
нx
M
sin
M
sin
k
Vv
.
2
1
1
2
2
+
−β
−=
k
M
sin
V
н
н
В результате, для проекции скорости возмущений на ось
x имеем
выражение
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β
+
−=
2
2
1
1
2
н
нx
M
sin
k
Vv
.
Проекция скорости возмущений на ось
y
определяется аналогич-
ным образом из второй формулы (37):
()
=
ϖβ+ϖβ
ϖβ
=
ϖ−β
ϖβ
=
sinsincoscos
sincos
V
cos
sincos
Vv
ннy
β+ϖ
=
tgctg
V
н
1
.
Используя формулу
ϖ
ϖ
tg
ctg
1
=
и учитывая равенство (35), можно
записать:
=
β+
−β
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β−
+
β
=
tg
M
sin
M
sin
k
tg
Vv
н
н
нy
2
2
2
2
1
1
2
1
1
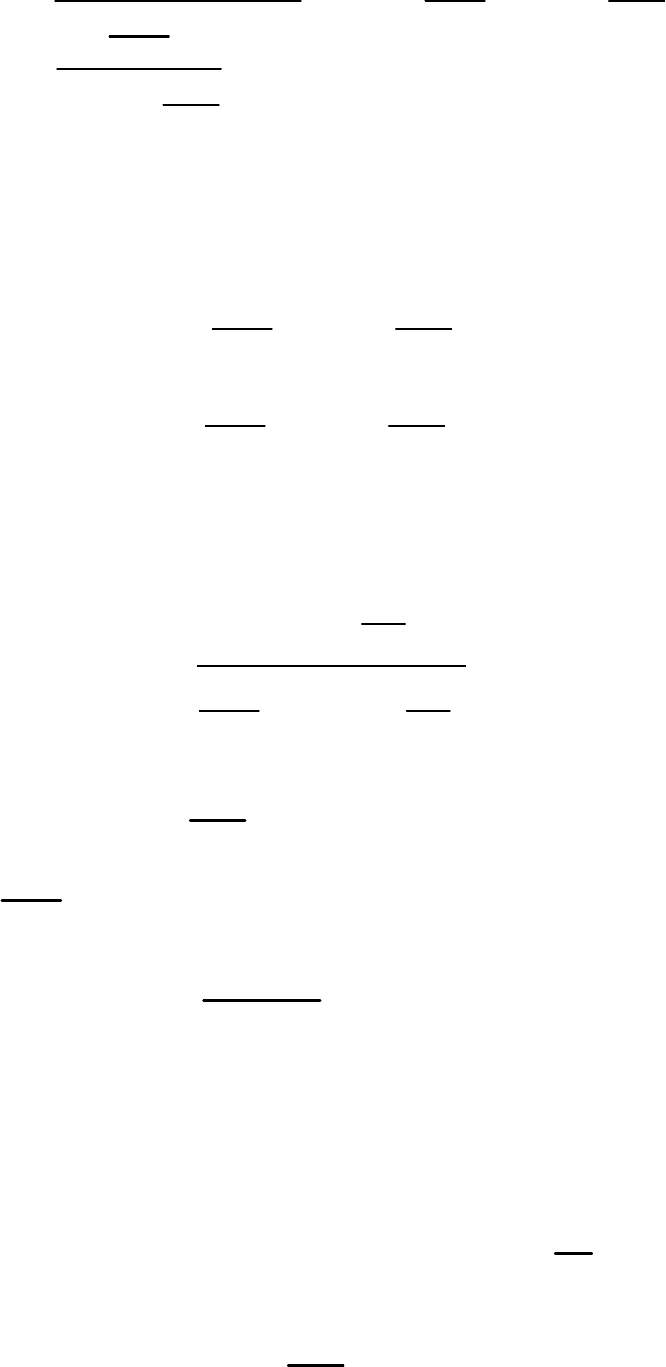
24
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β
+
β=
+−
−β
+
β=
2
2
2
2
1
1
2
11
1
2
1
1
н
н
н
н
M
sin
k
сtgV
M
sin
k
сtgV
.
Таким образом, компоненты скорости возмущённого движения,
вызванного обтеканием внутреннего угла, могут быть найдены по
формулам:
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β
+
β=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β
+
−=
.
M
sin
k
ctgVv
,
M
sin
k
Vv
н
нy
н
нx
2
2
2
2
1
1
2
1
1
2
(38)
Проанализируем уравнение (35) при гиперзвуковых скоростях об-
текания (
5>М ):
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β−
+
−β
β=ϖ
2
2
2
2
1
2
1
1
н
н
M
sin
k
M
sin
ctgtg
. (35)
В этом случае член
2
1
н
M
можно отбросить, и если считать, что
выражение
2
1+k
приближённо равно единице, то можно записать:
β=β⋅β=
β−
β
β≈ϖ tgtgctg
sin
sin
ctgtg
2
2
2
1
.
Следовательно, при гиперзвуковых скоростях угол наклона фрон-
та скачка
β близок к углу отклонения потока на скачке ϖ , в связи с чем
слой уплотнённого газа, расположенный между фронтом скачка и по-
верхностью тела, оказывается очень тонким.
В достаточно интенсивных скачках уплотнения
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
>> 10
н
p
p
всегда
имеет место неравенство
2
1
н
M
sin >>β . (39)
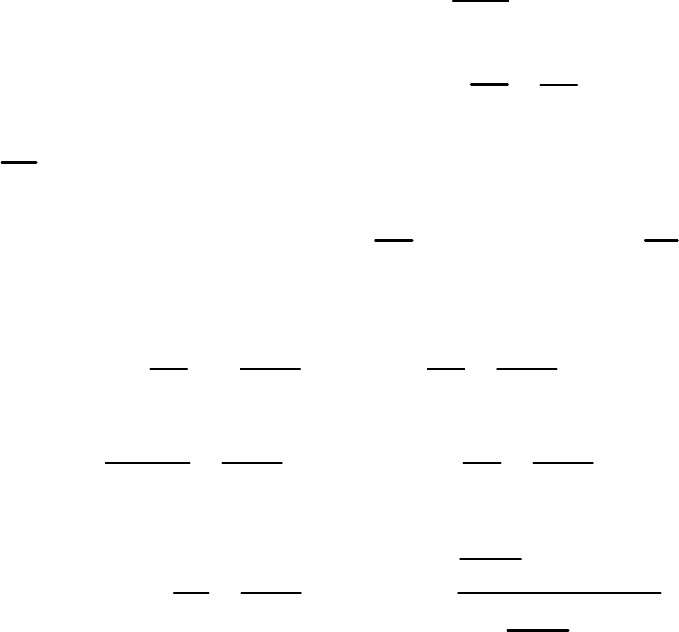
25
При любом сколь угодно малом фиксированном значении угла от-
клонения потока
ϖ можно достичь такого значения числа Маха, при
котором условие (39) будет выполнено. Поэтому в соотношениях (30) –
(38) можно пренебречь членами
2
1
н
M
, и тогда оказывается, что без-
размерные скорости возмущения
н
x
V
v
,
н
y
V
v
, безразмерная плотность
н
ρ
ρ
и угол наклона фронта скачка β не зависят от числа
н
М , а безраз-
мерные значения давления
н
p
p
(и температуры
н
T
T
) пропорциональны
величине
2
н
М
:
β
+
−=
2
1
2
sin
kV
v
н
x
,
ββ
+
= cossin
kV
v
н
y
1
2
; (40)
β
+
=
ρ
−
2
2
1
2
sin
k
V
pp
н
н
н
, или β
+
=
2
2
1
2
sinM
k
k
p
p
н
н
; (41)
1
1
−
+
=
ρ
ρ
k
k
н
,
β
+
−
ββ
+
=ϖ
2
1
2
1
1
2
sin
k
cossin
k
tg
. (42)
Таким образом, при больших гиперзвуковых скоростях в области
за интенсивными скачками уплотнения наблюдается некоторое пре-
дельное состояние газового течения, при котором характеризующие
его безразмерные параметры и аэродинамические коэффициенты не
зависят от значения числа
н
М
. Аналогичные особенности газового те-
чения наблюдаются при очень малых дозвуковых скоростях (
0→
н
М ),
когда свойства потока также не зависят от значения числа
н
М (несжи-
маемая жидкость).
Таким образом, по числам маха существует два режима автомо-
дельности: при малых дозвуковых скоростях и при больших сверхзву-
ковых скоростях.
Опыты показывают, что автомодельность при больших сверхзву-
ковых скоростях (при
∞→
н
М ) практически достигается при сравни-
тельно умеренных значениях числа
н
М . Об этом свидетельствуют, на-
пример, экспериментальные данные о коэффициентах сопротивле-
ния сферы и цилиндра с конической головной частью, изображённые
на рис. 8.
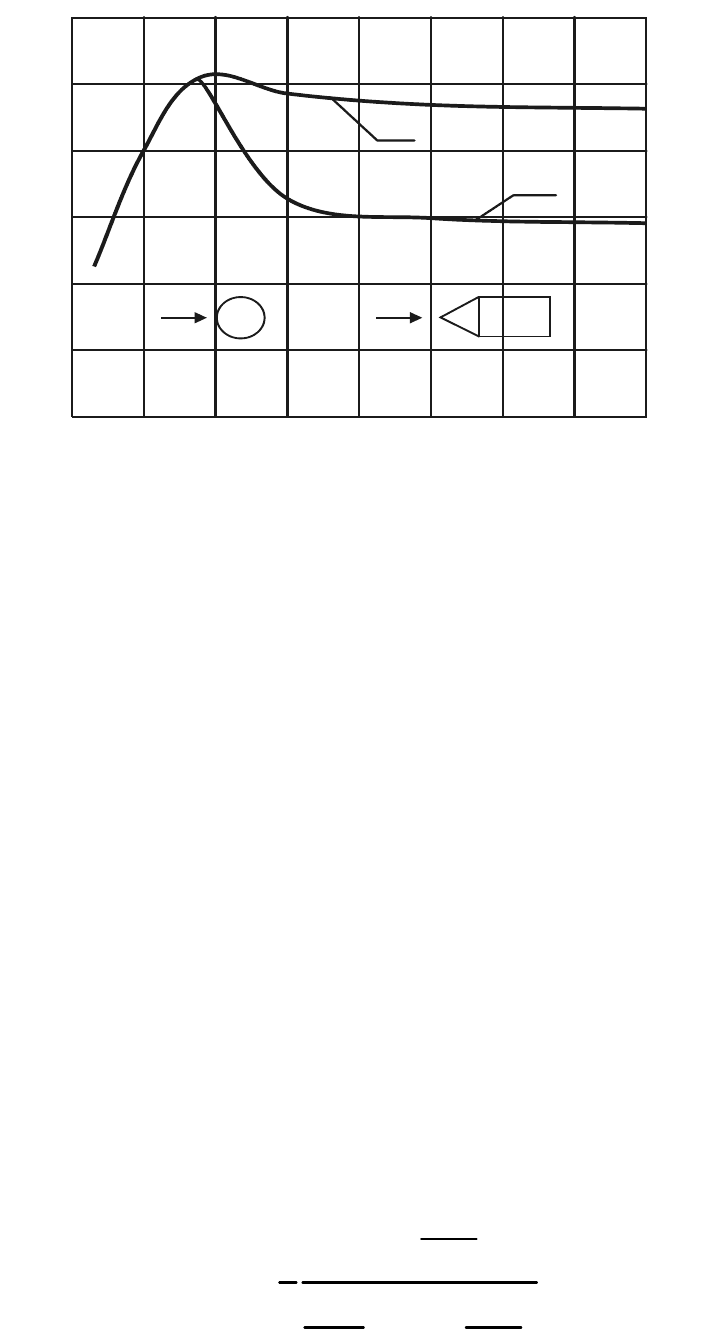
26
x
C
н
M
.80
.40
8
6420
2
1
Рис. 8. Зависимость коэффициентов сопротивления
от числа Маха: 1 – сфера, 2 – цилиндр
с конусом
На данном рисунке показаны графики изменения указанных коэффи-
циентов в зависимости от начального значения числа Маха
н
М . Кри-
вая, помеченная индексом
1, соответствует обтеканию сферы, а кри-
вая с индексом
2
показывает обтекание цилиндра с конической голов-
ной частью. Угол полураствора конуса данной головной части равен
°30
.
Как видно из рис. 8, уже при
43...М
н
=
величины
x
C весьма близки
к асимптотическим значениям, соответствующим
∞→
н
М . Стабиль-
ность значений аэродинамических коэффициентов свидетельствует о
неизменности всей картины течения газа вблизи тела.
Если ударная волна недостаточно интенсивна, т.е. угол отклоне-
ния потока
ϖ
в ней мал, то при гиперзвуковой скорости угол
β
также
мал.
Производя следующие замены:
β≈βsin , ϖ≈ϖsin , 1≈βcos , 1≈ϖcos , (42
1
)
из равенства (35) можно получить:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β−
+
−β
β
=ϖ
2
2
2
2
1
2
1
1
1
н
н
M
k
M
.
Принято вводить следующие обозначения:

27
н
MK β=
β
и
н
MK ϖ=
ϖ
. (42
2
)
Тогда полученное равенство может быть переписано таким обра-
зом:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β−
+
−
β=ϖ
β
β
2
2
2
1
1
2
1
1
1
K
k
K
. (43)
В рассматриваемом случае
1<<β
, поэтому, умножив обе части
равенства (30) на число Маха
н
М , запишем
2
1
1
1
2
+
−
=
β
βϖ
k
K
KK
. (44)
Равенство (44)
можно переписать как квадратное уравнение отно-
сительно величины
β
K :
01
2
1
2
=−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
βϖβ
KK
k
K .
Решение данного квадратного уравнения имеет следующий вид:
1
4
1
4
1
2
+
⎟
⎠
⎞
⎜
⎝
⎛
+
±
+
=
ϖϖβ
K
k
K
k
K .
Из физических соображений второе решение со знаком «-» не
имеет смысла, т.к. выполняется неравенство
1
4
1
4
1
2
+
⎟
⎠
⎞
⎜
⎝
⎛
+
<
+
ϖϖ
K
k
K
k
,
и, следовательно, величина
β
K
получается отрицательной, что невоз-
можно.
Таким образом, на гиперзвуковых скоростях обтекания при малом
угле отклонения потока
ϖ
угол наклона скачка уплотнения можно оп-
ределить по формуле
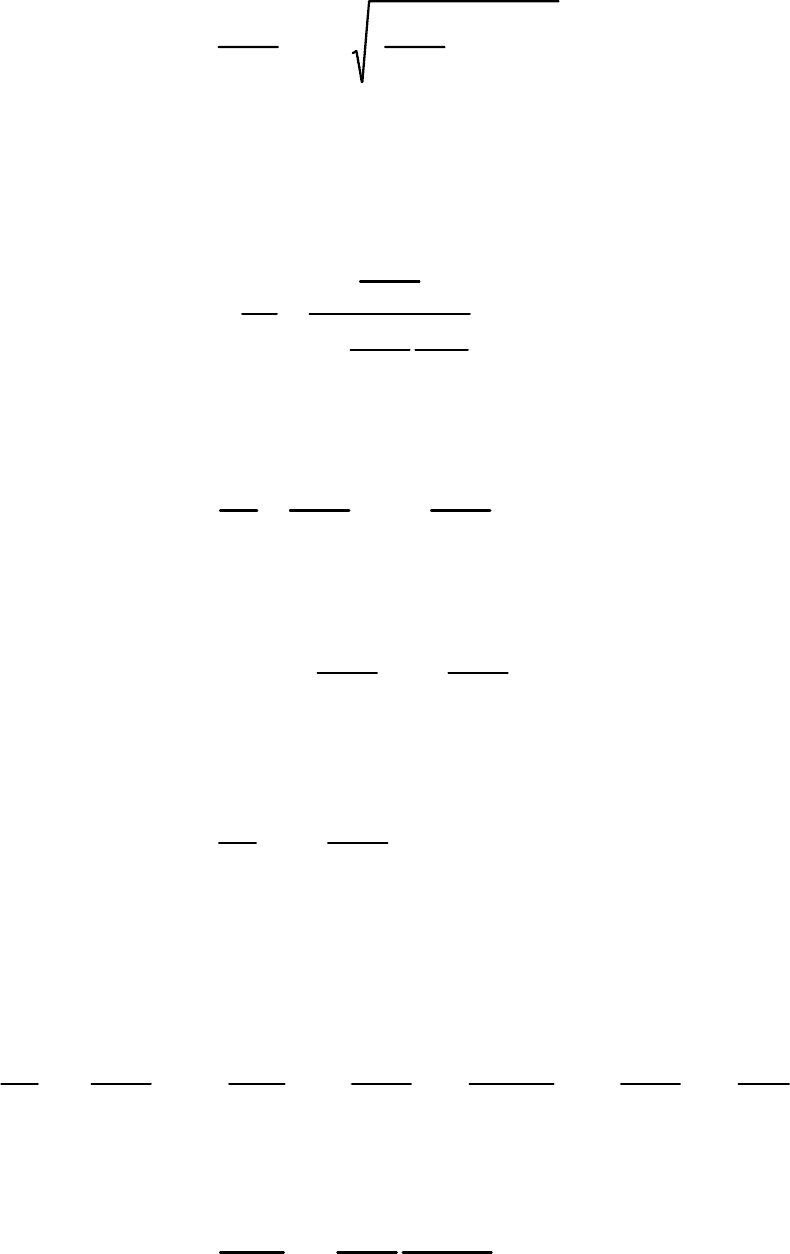
28
1
4
1
4
1
2
+
⎟
⎠
⎞
⎜
⎝
⎛
+
+
+
=
ϖϖβ
K
k
K
k
K . (45)
Остальные параметры течения при малом угле отклонения потока
получаем аналогичным образом.
Соответственно, из равенства (30) вытекает формула для опреде-
ления отношения плотностей на скачке уплотнения:
2
1
1
2
1
1
1
н
н
K
k
k
k
−
+
−
+
=
ρ
ρ
. (46)
Из равенства (22) можно получить отношение давлений в рас-
сматриваемом течении:
1
1
1
2
2
+
−
−
+
=
β
k
k
K
k
k
p
p
н
. (47)
Используя очевидное соотношение
1
2
1
1
1
+
−=
+
−
−
k
k
k
k
,
формулу для отношения давлений часто записывают в другом, более
удобном, виде:
(
)
1
1
2
1
2
−
+
+=
β
K
k
k
p
p
н
. (48)
Скорости возмущений могут быть найдены из равенств (38). С
учётом равенств (42
1
) проекция искомой скорости на ось x определя-
ется следующим образом:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
β
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
β
−
+
β
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β
+
−=
β
2
2
2
2
2
2
2
1
1
1
21
1
1
21
1
2
K
k
M
k
M
kV
v
нн
н
x
.
Полученную формулу принято записывать в таком виде:
2
2
2
1
1
2
β
β
−
+
−=
β
K
K
k
V
v
н
x
. (49)
Из формулы (44) следует равенство
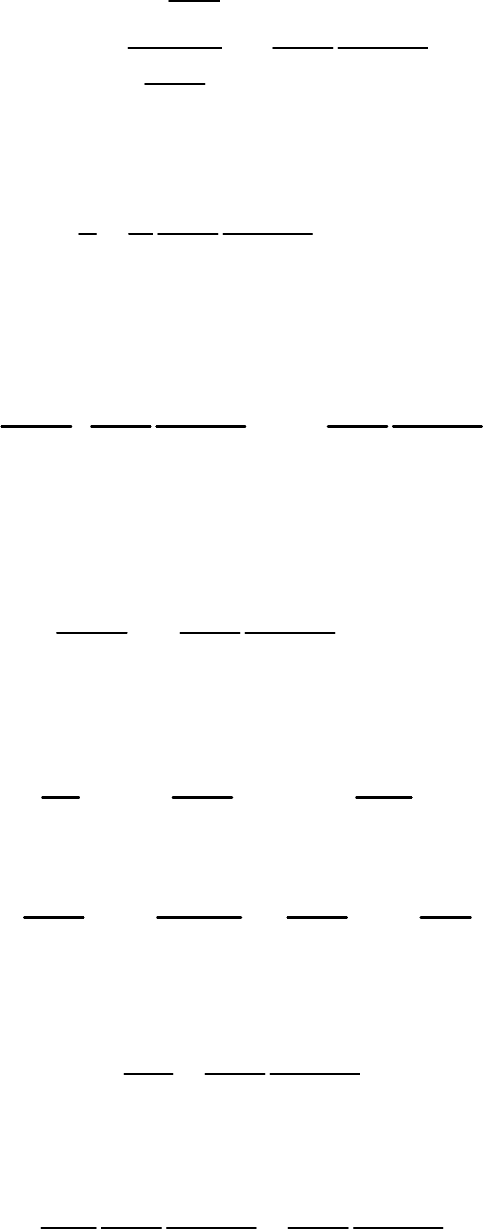
29
2
22
1
1
2
2
1
1
1
β
ββ
−
+
β=
+
−
β=ϖ
K
K
k
k
K
.
Полученное равенство может быть переписано в виде
2
2
1
1
211
β
β
−
+ϖ
=
β
K
K
k
. (50)
Тогда из формулы (34) следует такое соотношение:
2
2
2
2
2
2
1
1
2
1
1
2
β
β
β
β
−
+
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
ϖ
K
K
k
K
K
k
V
v
н
x
,
и окончательный результат для скорости
x
v
записывается следующим
образом:
1
2
1
2
2
2
−
+
−=
ϖ
β
β
K
K
k
V
v
н
x
. (51)
Для скорости
y
v выполняются аналогичные преобразования:
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β
+
β=
2
2
1
1
2
н
н
y
M
sin
k
ctg
V
v
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−β
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
β
−β
+
=
β
2
2
2
1
1
1
21
1
1
2
K
k
M
k
н
.
Отсюда следует такой результат:
2
2
1
1
2
β
β
−
+
=
β
K
K
kV
v
н
y
.
Учитывая соотношение (50), можно записать:
2
2
2
2
1
1
2
1
1
2
β
β
β
β
−
+
=
−
+ϖ
K
K
k
K
K
kV
v
н
y
,
поэтому скорость возмущений
y
v в данном случае вычисляется по
формуле

30
1=
ϖ
н
y
V
v
. (51
1
)
Найдём теперь число Маха за скачком уплотнения. Для этого с
учётом равенства
a
V
M =
запишем тождественное выражение:
1
22
2
≡
Ma
V
.
Скорость звука определяется по формуле
ρ
=
p
ka
2
, поэтому пре-
дыдущее тождество принимает следующий вид:
1
2
2
≡
ρ
kpM
V
.
Приравняем два записанных комплекса параметров для начально-
го и текущего состояний:
1
2
2
2
2
≡
ρ
≡
ρ
н
н
нн
Mkp
V
kpM
V
.
Отсюда определяется число Маха после скачка уплотнения:
н
н
н
н
p
p
V
V
MM
ρ
ρ
=
2
2
2
2
. (52)
Как следует из равенств (49) и (51
1
), в случае гиперзвукового те-
чения скорость возмущений газа на скачке при малом угле пренебре-
жимо мала по сравнению со скоростью невозмущённого потока. Сле-
довательно, скорость на скачке почти не изменяется (
н
VV ≈ ). Тогда из
равенства (52) с помощью соотношений (46) и (47) получается сле-
дующая формула:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
β
+
+
+
−
⎥
⎦
⎤
⎢
⎣
⎡
+
−
−β
+
≈
2
2
2
2
2
2
1
1
2
1
1
1
1
1
2
н
н
н
M
kk
k
k
k
M
k
k
M
M
. (53)
В предельном случае, когда
∞→
2
н
M , можно записать:
1
1
1
2
2
2
2
2
+
−
β
+
≈
k
k
M
k
k
M
M
н
н
,
и для числа
M
вытекает следующее выражение:
