Тюрев В.В. Гиперзвуковые течения газа
Подождите немного. Документ загружается.

61
На левом рисунке модуль производной
T∂
ϕ∂
меньше 1. На рис. 26
показан график функции
()
Tϕ и для иллюстрации способа решения
задачи приведена прямая
TT = .
Полученное уравнение удобно преобразовать к виду (73) следую-
щим образом:
4
стrст
ТTТ
α
εσ
+= . (74)
В данном случае рассматриваемая производная имеет вид
3
4
ст
ст
Т
Т α
εσ
=
∂
∂ϕ
.
Значит, такой записью уравнения для метода последовательных
приближений можно пользоваться для температур, определяемых не-
равенством
14
3
<
α
εσ
ст
Т . Если в качестве первого приближения вы-
брать
rст
TT =
(
ст
T
всегда
r
T<
), то получим 14
3
<
α
εσ
r
T . Когда
r
T
дос-
таточно велико и предыдущее неравенство не выполняется, то ре-
шаемое уравнение (72) нужно переписать в следующем виде:
⎟
⎠
⎞
⎜
⎝
⎛
α
εσ
−−λ+=
4
стrстстст
TТTTT
,
(75)
где
λ – параметр, который вводится в уравнение для того, чтобы в по-
лученном уравнении (75) обеспечивалось требование
1<
∂
ϕ∂
T
.
Очевидно, что уравнения (74) и (75) эквивалентны при любом вы-
боре параметра
λ , т.к. из уравнения (74) следует, что в уравнении (75)
при верно определённой величине
ст
T выражение в скобках должно
равняться нулю, и уравнение (75) будет удовлетворяться.
Здесь функция
ϕ
, введенная в рассмотрение по формуле (73),
имеет вид
()
⎟
⎠
⎞
⎜
⎝
⎛
α
εσ
−−λ+=ϕ
4
стrстстст
TТTTT
и анализируемая производная зависит от введенного параметра
λ :
⎟
⎠
⎞
⎜
⎝
⎛
α
εσ
−λ+=
∂
∂ϕ
3
411
ст
ст
T
T
.

62
Параметр
λ необходимо выбрать таким, чтобы выполнялось не-
равенство
1<
∂
∂ϕ
ст
T
.
Желательно, чтобы в дополнение к записанному требованию к
производной величина
ст
T∂
∂ϕ
была меньше нуля, тогда истинное зна-
чение корня лежит между двумя, идущими одно вслед другому при-
ближениями, и просто оценивается погрешность решения, так как она
всегда не больше, чем разница между двумя последними приближе-
ниями.
11. СВОБОДНО-МОЛЕКУЛЯРНЫЕ ТЕЧЕНИЯ ГАЗА
Гипотеза сплошности среды, широко применяемая при исследо-
вании достаточно плотных газов, в условиях разреженных газов непри-
годна.
Воздух в земной атмосфере при нормальных условиях на уровне
моря в
3
1 см содержит
19
106872 ⋅. молекул, длина среднего свободно-
го пробега молекулы равна
м,
8
10636
−
⋅
, среднее расстояние между
центрами молекул –
см
6
10
3
1
−
⋅ . Каждая молекула в одну секунду ис-
пытывает до 10 млрд (
10
10 ) столкновений. Если молекулы газа столк-
нутся с движущимся телом, то они почти мгновенно за время, намного
меньшее, чем характерное время процесса
τ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=τ
хар
хар
V
l
, через соуда-
рения с другими молекулами передадут им часть кинетической энер-
гии, и возмущающее действие тела распространится на всю окружаю-
щую тело среду.
С увеличением высоты уменьшается плотность воздуха, и длина
свободного пробега молекул может стать соизмеримой, а затем пре-
взойти размеры обтекаемого тела. В этом случае отразившиеся от те-
ла молекулы, могут столкнуться с другими молекулами только вдали
от тела. Таким образом, возмущающее действие тела не будет рас-
пространяться на непосредственно окружающую его среду и гипотеза
сплошности теряет смысл. Значит, необходимо учитывать молекуляр-
ную структуру газа.
При свободно-молекулярном течении, как уже указывалось, моле-
кулы, отраженные от тела, движущегося в неограниченном потоке, не
оказывают влияния на невозмущенный поток. Следовательно, в окре-
стности обтекаемого тела не должны возникать ударные волны и не
должен образовываться «пограничный слой».

63
На основании этих соображений при расчете теплопередачи и
аэродинамических характеристик тел, движущихся в свободно-
молекулярном потоке, можно рассматривать независимо два течения:
течение, образованное молекулами, сталкивающимися с телом при
его движении, и течение, образованное молекулами, отраженными от
тела или испускаемыми им.
При вычислении потока количества движения или энергии моле-
кул, достигающих поверхности тела, предполагается, что газ нахо-
дится в состоянии местного максвелловского равновесия. Поэтому ре-
зультаты таких вычислений при рассмотрении течений на больших вы-
сотах необходимо использовать с некоторой осторожностью, так как в
настоящее время наши знания о состоянии и составе верхней атмо-
сферы все еще ограничены.
12. РЕЖИМЫ ТЕЧЕНИЯ ГАЗА
При изменении длины свободного пробега молекул изменяется и
характер взаимодействия тела с окружающей средой. Существенным
параметром, влияющим на аэродинамические характеристики летяще-
го тела, является средняя длина свободного пробега частицы
l
– ста-
тистически средняя величина расстояния, проходимого частицами
среды между последовательными столкновениями.
Изменение величины
l
в зависимости от высоты над уровнем
земли (для нейтральных частиц) приведено в табл. 1.
Таблица 1
Изменение характерных параметров атмосферы по высоте
Н[км] l[м] Т[град K] p[Н/м
2
]
ρ
[кг/м
3
]
0
6.6 10
-8
288
1.013 10
5
1.22
10 2.0 10
-7
223 25000 0.42
20
9.1 10
-7
216
5400
0.088
30
4.4 10
-6
226
1100
0.018
40
2.0 10
-5
250
314
4.2 10
-3
50
7.9 10
-5
270
90
1.15 10
-3
60
2.6 10
-4
247
25
3.5 10
-4
70
9.8 10
-4
220
6.1
1.1 10
-4
80
4.4 10
-3
198
1.26
1.7 10
-5
90
2.4 10
-2
187
0.23
4.1 10
-6
100
1.4 10
-2
196
0.054
7.2 10
-7
120
2.9
334
7.9 10
-3
6.6 10
-8
140
15.7
559
2 10
-3
1.3 10
-8
160
53.4
695
7.7 10
-3
3.4 10
-8
180
120
775
3.8 10
-4
1.3 10
-8
200
233
854
2.2 10
-4
6.3 10
-10
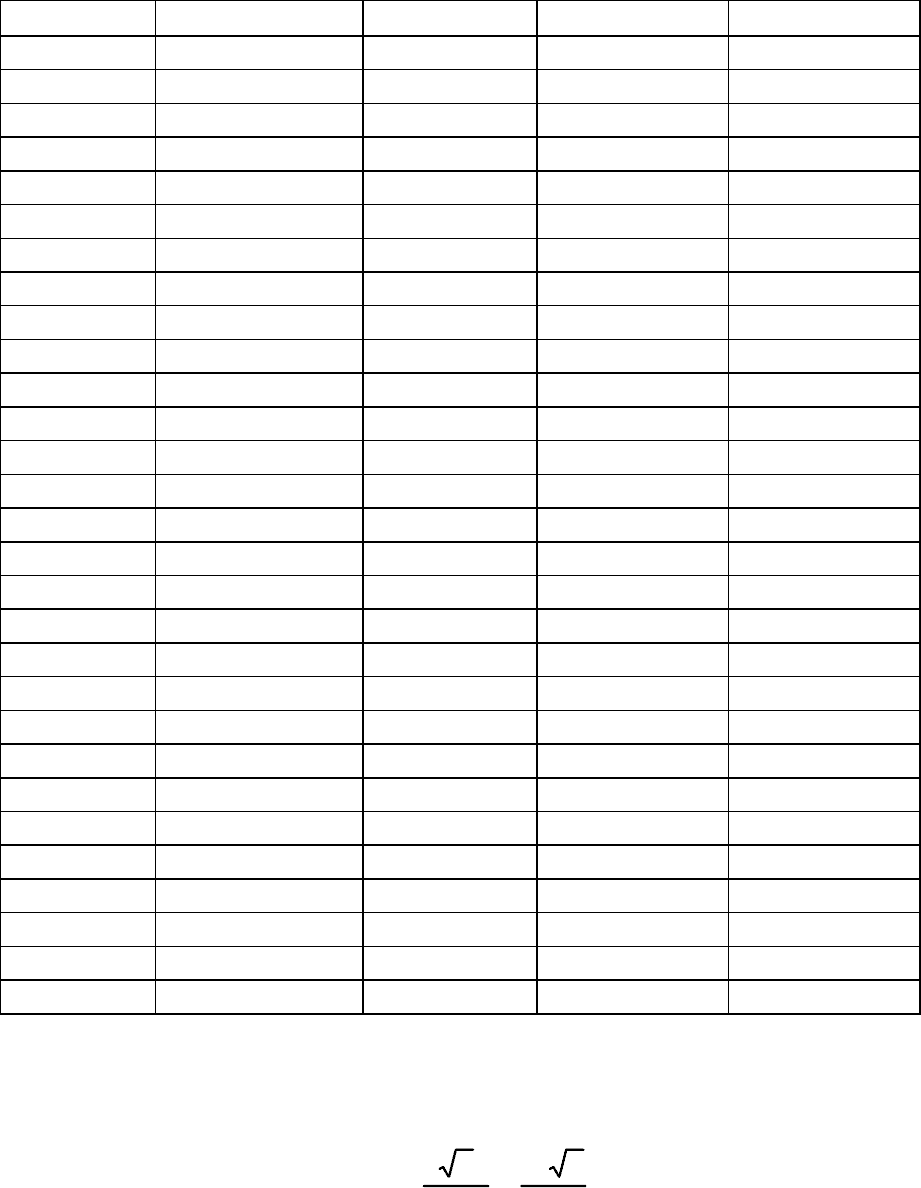
64
Окончание табл. 1
Н[км] l[м] Т[град K] p[Н/м2]
ρ
[кг/м3]
220
418
889
1.3 10
-4
3.4 10
-10
240 697 924 3.09 10
-4
7.8 10
-11
260 1115 947 1.98 10
-5
4.73 10
-11
280 1722 959 1.3 10
-5
2.97 10
-11
300 2596 970 8.71 10
-6
1.91 10
-11
320 3936 981 5.81 10
-6
1.2310
-11
340 5903 987 3.9 10
-6
8.04 10
-12
360 8008 990 2.88 10
-6
5.80 10
-12
380 11380 993 2.03 10
-6
4.00 10
-12
400 15990 995 1.45 10
-6
2.79 10
-12
420 22293 996 1.04 10
-6
1.98 10
-12
440 30889 996 7.52 10
-7
1.40 10
-12
460 42175 997 5.51 10
-7
1.01 10
-12
480 57306 997 4.06 10
-7
7.22 10
-13
500 77181 998 3.01 10
-7
5.21 10
-13
550 1.537 10
5
999 1.51 10
-7
2.38 10
-13
600 2.84 10
5
1000 8.21 10
-8
1.13 10
-13
650 4.77 10
5
1000 4.88 10
-8
5.72 10
-14
700 7.31 10
5
1000 3.19 10
-8
3.08 10
-14
750 1.03 10
6
1000 2.26 10
-8
1.79 10
-14
800 1.3710
6
1000 1.70 10
-8
1.14 10
-14
850 1.73 10
6
1000 1.31 10
-8
7.79 10
-15
900 2.14 10
6
1000 1.09 10
-8
5.76 10
-15
950 2.59 10
6
1000 8.98 10
-9
4.43 10
-15
1000 3.11 10
6
1000 7.51 10
-9
3.56 10
-15
1050 3.56 10
6
1000 6.55 10
-9
3.04 10
-15
1100 4.08 10
6
1000 5.72 10
-9
2.60 10
-15
1150 4.65 10
6
1000 5.01 10
-9
2.24 10
-15
1200 5.26 10
6
1000 4.43 10
-9
1.95 10
-15
Средняя длина свободного пробега
l
может быть подсчитана по
формуле, известной из кинетической теории газов:
ρπ
=
π
=
22
22
r
m
rn
l
,
где
n
– число молекул в см
3
;
r
– эффективный радиус молекулы;
nm=ρ – плотность газа; т – масса молекулы.
Так как эффективный радиус не может быть определён непосред-
ственным измерением, то более целесообразно выразить длину

65
свободного пробега
l
через количественно измеряемые величины, на-
пример через вязкость газа. В соответствии с данными кинетической
теории газа динамический коэффициент вязкости может быть записан
следующим образом:
lV.
ср
ρ=µ 4990 ,
где
ср
V – средняя скорость молекул, связанная со скоростью звука a
соотношением
8
k
Va
ср
π
=
.
Следовательно, длину свободного пробега можно вычислить по
формуле
a
k.l
ρ
µ
= 2551
. (76)
При очень больших разрежениях реализуется свободно-
молекулярный режим. В этом случае длина свободного пробега моле-
кул в несколько раз больше размеров тела.
С уменьшением разрежения, когда длина свободного пробега мо-
лекул соизмерима с размерами тела, реализуется переходный режим.
При умеренном разрежении, когда длина свободного пробега мо-
лекул мала по сравнению с характерным размером тела, имеет место
течение со скольжением.
В качестве параметра, характеризующего режимы течения, при-
нимают число Кнудсена
L
l
Kn =
,
где
l
– длина свободного пробега;
L
– характерный размер тела.
Величину
l
можно взять из приведенной выше таблицы.
При наличии пограничного слоя число Кнудсена определяется по
толщине пограничного слоя
δ :
δ
=
δ
l
Kn
.
Число
δ
Kn можно выразить через известные критерии подобия.
С использованием определений для введённых выше чисел Кнуд-
сена получаем соотношение
δ
=
δ
l
KnKn
. (77)
Число Кнудсена, согласно формуле (76) и с учетом равенства
ρ
µ
=ν
,

66
где
ν – кинематический коэффициент вязкости, можно записать сле-
дующим образом:
aLV
V
k.
aL
k.
L
l
Kn
ν
=
ρ
µ
== 25512551
.
Окончательно, выражение для числа Кнудсена через известные
критерии подобия преобразуется к виду
Re
M
k.Kn 2551= ,
где в выражения для чисел
Kn и Re входит одна и та же харак-
терная длина.
С учётом равенства (77) можно записать:
δ
=
δ
l
Re
M
k.Kn 2551
.
Так как толщина пограничного слоя
δ зависит от чисел Маха и
Рейнольдса, то границы течений также должны определяться ком-
плексом параметров из чисел
M
и Re .
Разделение газовой динамики на различные режимы течения, ос-
новывающееся на характерных значениях соответствующего числа
Кнудсена, является весьма условным. Наиболее часто принимают, что
влияние разреженности газа следует учитывать, если длина свободно-
го пробега превышает 1 % от толщины пограничного слоя. Это значе-
ние соответствует границе между течением сплошной среды и «тече-
нием со скольжением».
Следовательно, газовая динамика континуума соответствует зна-
чениям
010.
l
<
δ
.
Так как, согласно теории ламинарного пограничного слоя, при дос-
таточно больших числах Рейнольдса
ReL
1
≈
δ
,
то, с учётом записанных выше равенств, получаем следующие соот-
ношения:
01025512551 .
Re
Mk
.
aL
Rek
.
l
<=
ρ
µ
=
δ
.
Таким образом, приближённо границу целесообразности приме-
нения гипотезы сплошности среды можно записать в виде
010.
Re
M
< .
Эпюра скоростей в пограничном слое для течения сплошной сре-
ды показана на рис. 27, а.
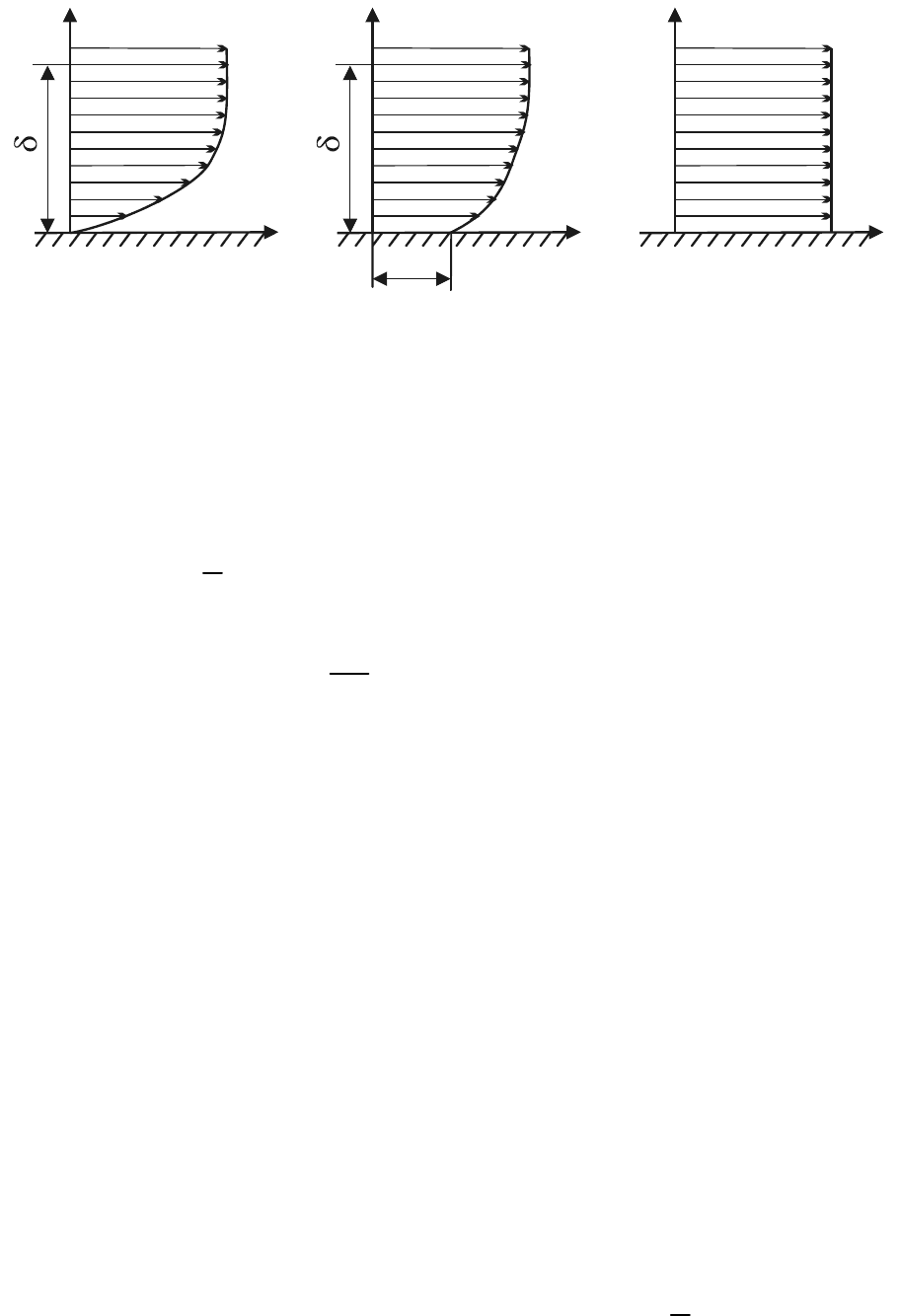
67
X
Y
v
0
X
Y
r
v
v
0
X
Y
v
0
Рис. 27. Течение газа вблизи твёрдой границы:
а – течение б – течение в – свободно-
сплошной среды; со скольжением; молекулярное течение
При очень малых числах Рейнольдса в качестве характерного
размера следует принять не толщину пограничного слоя, а некоторый
линейный размер (например, диаметр
L
канала). В этом случае число
Кнудсена равно
L
l
и в качестве границы течения континуума можно
принять:
010.
Re
M
< при
1<Re
.
За областью течения сплошной среды находится область «тече-
ния со скольжением». Для «течения со скольжением» не справедлива
гипотеза прилипания. Такое течение характеризуется, в частности,
тем, что слой газа, примыкающий к поверхности тела, имеет конечную
составляющую скорости, касательную к телу.
Течение со скольжением возникает в том случае, когда свободный
пробег молекул
l
не пренебрежимо мал по сравнению с толщиной по-
граничного слоя
δ
,но значительно меньше последней:
δ<l
, то про-
филь скорости направленного движения газа имеет форму, изобра-
жённую на рис. 27, б.
При расчёте «течения со скольжением» также можно использо-
вать уравнения газовой динамики сплошной среды. Однако при иссле-
довании таких течений следует в граничные условия на твёрдой по-
верхности вводить поправку на так называемое «скольжение» и «ска-
чок температуры».
В качестве верхней границы области «течения со скольжением»
(т.е. течений, характеризующихся, в частности, тем, что слой газа,
примыкающий к поверхности тела, имеет конечную, касательную к те-
лу, составляющую скорости) принимают значение
L
l
порядка 10 %.
Следовательно, область течения со скольжением ограничена преде-
лами
68
10010 .
Re
M
. << при 1>Re ;
10010 .
Re
M
. << при 1<Re .
При очень больших значениях числа Кнудсена (
1>>Kn ) погранич-
ный слой у поверхности тела не образуется, так как реэмитированные
(отражённые) поверхностью тела молекулы сталкиваются с молекула-
ми внешнего потока на далёком от тела расстоянии. Таким образом,
тело не вносит искажений в поле скоростей внешнего потока. Эта об-
ласть течения называется областью «свободно-молекулярного тече-
ния газа».
По имеющимся данным такое течение наблюдается при
3>
Re
M
.
Профиль скоростей свободно-молекулярного течения показан на
рис. 27, в. В рассматриваемой области трение и теплообмен на по-
верхности обтекаемого тела рассчитываются из условия однократного
столкновения молекул газа с поверхностью.
Переходная область между режимом со скольжением и свободно-
молекулярным режимом представляет собой большую сложность для
изучения, так как в ней приходится учитывать как столкновение моле-
кул между собой, так и неоднократные столкновения их с телом, а это
создаёт большие теоретические трудности.
Каждый режим течения газа реализуется в определенном диапа-
зоне изменения чисел Кнудсена. Строгих границ между течениями
провести нельзя. Полученные выше границы носят условный характер,
но точность результатов расчётов по изложенной выше методике
удовлетворяет требованиям, предъявляемым в настоящее время к
подобным исследованиям.
Ниже приведена сводка границ описанных областей:
010.
Re
M
< – течение сплошной среды;
10010 .
Re
M
. <≤ – течение со скольжением;
310 <≤
Re
M
;
Re
M
. – переходный режим;
3≥
Re
M
– свободно-молекулярное течение.
Это разграничение удобно тем, что нет необходимости вычислять
толщину пограничного слоя. Коэффициент
ν
, входящий в число
R
e ,
можно вычислить из формулы
a
k.l
ν
= 2551
,
в результате получается следующее выражение:
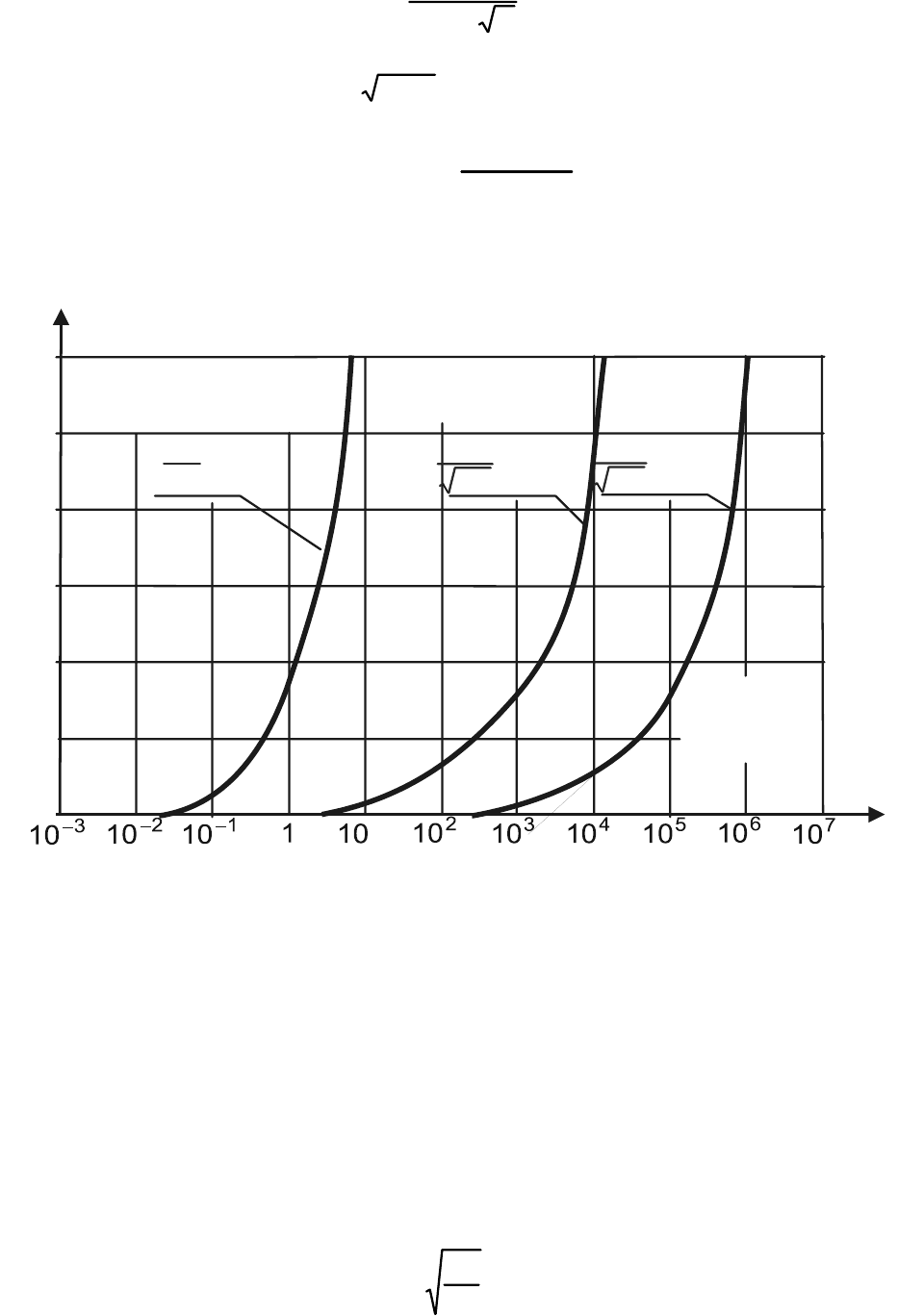
69
0
2
4
6
8
10
Свободно-молекуляр-
ное течение
Переходный
режим
Скольже-
ние
Течение
сплошной
среды
10.
Re
M
=
3
=
Re
M
010.
Re
M
=
Re
M
12
Рис. 28. Границы различных режимов течения разреженного газа
k.
la
2551
=ν
.
Длину свободного пробега
l
находим из табл. 1, скорость звука
определяем по формуле
kRTa = .
Газовая постоянная имеет следующее значение:
градкг
дж
R
⋅
= 287
.
На рис. 28 показаны описанные выше области различных режимов
течения газа и границы приведенных режимов.
Сопоставляя данные рис. 28 с длиной свободного пробега из табл.
1, можно получить представление о связи между высотой полёта и
границами различных режимов. Для ракеты длиной 3 м влияние
скольжения начинается с высоты 50 км при
1=
M
и 30 км при 4=
M
.
Свободно-молекулярное течение устанавливается при любой скорости
полёта, начиная с высоты 140 км.
Из кинетической теории газов следует, что средняя скорость бес-
порядочного движения молекул определяется по формуле
∞
π
= a
k
c
i
8
,
70
а наиболее вероятная скорость
m
c по формуле
∞
= a
k
c
m
2
.
13. МАКСИМАЛЬНАЯ РАДИАЦИОННАЯ ТЕМПЕРАТУРА
Пусть на рассматриваемую стенку, перпендикулярно ей, набегает
поток со скоростью
∞
V . На стенке выделяется элемент площади s
,
на
который
опирается цилиндрическая поверхность высотой
l
. Объём га-
за, находящегося внутри данной поверхности, определяется по фор-
муле
slW ⋅= .
Масса газа в выделенном объёме находится следующим образом:
ρ⋅⋅=ρ⋅= slWm
.
Кинетическая энергия газа в выделенном объеме вычисляется в
соответствии с равенством
22
22
∞∞
ρ
==
sVlmV
J
.
Эта энергия передается площадке за время
∞
=τ
V
l
. За единицу
времени площадке сообщается энергия
2
3
∞
ρ
=
τ
sV
J
, а на единицу
площади поставляется поток энергии, равный
2
3
∞
ρ
=
V
q
пост
. В резуль-
тате стенка нагревается до температуры
w
T и излучает поток энергии,
равный
4
wизл
Tq εσ= .
В равновесном состоянии температура стенки принимает такое
значение, что
излпост
qq = , тогда
4
3
2
w
T
V
εσ=
ρ
∞
и
3
4
w
V
T
2
ρ
εσ
∞
=
.
Величина
w
T
называется максимальной радиационной темпера-
турой.
