Тюрев В.В. Гиперзвуковые течения газа
Подождите немного. Документ загружается.

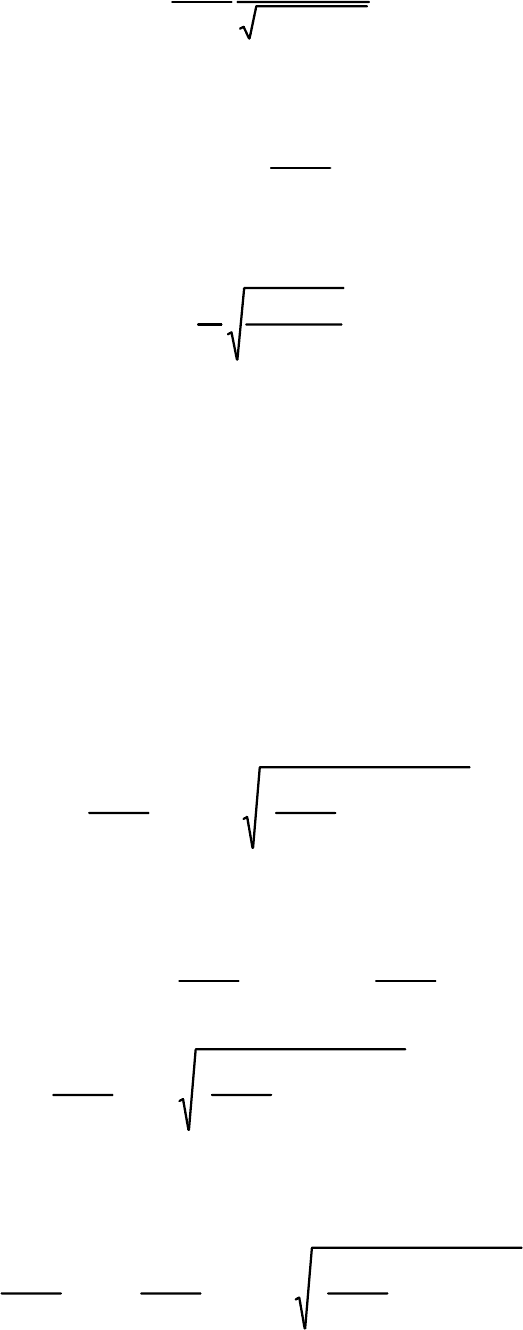
31
()
12
11
−
β
+
→
kk
k
M
.
При
н
M , стремящемся к бесконечности, согласно равенству (44),
2
1+
ϖ=β
k
.
Поэтому число Маха
M
стремится к такому пределу:
()
1
21
−ϖ
→
kk
M
.
Иначе говоря, в случае
∞→
2
н
M при малых углах наклона скачка
β число Маха за скачком будет большим. Если скачок имеет неболь-
шую интенсивность, то числа Маха перед скачком и за ним при гипер-
звуковой скорости имеют значения одного и того же порядка.
При рассмотрении течения Прандтля – Майера все параметры
были представлены в функции угла отклонения потока, тогда как для
течения за скачком найдены зависимости, содержащие угол наклона
самого скачка.
Для удобства вычислений необходимо выразить параметры тече-
ния газа после скачка уплотнения через угол поворота потока
ϖ
. Вы-
ражение (45) можно переписать в таком виде:
1
4
1
4
1
2
+
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
+ϖ
+
=β
ннн
M
k
M
k
M
.
Таким образом,
()
++
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
+
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
=−β=−
β
1
4
1
4
1
11
22
22
ннн
M
k
M
k
MK
11
4
1
2
1
2
−+
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
ϖ
+
+
нн
M
k
M
k
.
Искомое выражение для угла
β
через угол
ϖ
преобразуется к ви-
ду
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
+ϖ
+
ϖ
+
=−β 1
4
1
4
1
2
1
1
2
2
нннн
M
k
M
k
M
k
M . (54)

32
Для сильных возмущений, когда выполняется неравенство
∞→ϖ
н
M , данное равенство можно переписать таким образом:
()
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
++
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
=−β
2
2
2
4
1
1
11
4
1
21
н
нн
M
k
M
k
M
.
Следовательно, при больших числах Маха искомая формула име-
ет вид
()
2
2
2
1
1
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
≈−β
нн
M
k
M
. (55)
Подставляя равенство (55) в формулы (46) – (49), можно предста-
вить изменение давления и плотности на скачке уплотнения, а также
величины возмущений скорости в функции угла отклонения потока (уг-
ла встречи потока с поверхностью тела).
Для вычисления сил, действующих на тело в гиперзвуковом пото-
ке газа, необходимо знать распределение давления по поверхности
обтекаемого тела. Для сильных возмущений (
∞→ϖ
н
M ), с учётом ра-
венства (48), формула для изменения давления принимает такой вид:
2
2
1
1
2
1
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
+
+
+=
н
н
M
k
k
k
p
p
.
Легко видеть, что искомое давление может быть вычислено по
следующей формуле:
()
()
2
2
1
1 ϖ
+
+=
н
н
M
kk
p
p
. (56)
Из полученных зависимостей следует, что при гиперзвуковых ско-
ростях в плоском скачке уплотнения изменение параметров определя-
ется (как и в течении Прандтля – Майера) одним критерием
β=ϖ
н
MK
– произведением числа Маха на угол отклонения потока.
4. ОПРЕДЕЛЕНИЕ СИЛ, ДЕЙСТВУЮЩИХ НА ПЛОСКУЮ ПЛАСТИНУ,
НА БОЛЬШИХ СВЕРХЗВУКОВЫХ СКОРОСТЯХ
ПРИ МАЛОМ УГЛЕ АТАКИ
Полученные выше результаты дают возможность вывести про-
стые формулы для коэффициентов подъёмной силы и лобового со-
противления пластины, обтекаемой газовым потоком с гиперзвуковой
скоростью при малом угле атаки (рис. 9).

33
y
x
O
B
A
нижн
V
верх
V
∞
V
C
3
C
2
C
1
Рис. 9. Схема обтекания плоской пластины
Как известно, при обтекании любого тела сверхзвуковым потоком
возмущения, вызванные телом в потоке газа, вперёд против потока не
передаются. Поэтому часть линии тока
AO
, расположенная перед
пластиной, остаётся прямой линией. В потоке невязкой жидкости или
газа любая линия тока может рассматриваться, как граница потока.
Задача обтекания пластины потоком газа, в связи с указанным обстоя-
тельством, может быть разбита на две задачи:
1) изучение течения выше линии
AOBx ;
2) изучение течения ниже линии
AOBx .
Первая задача исследует обтекание внешнего угла и выше рас-
сматривалась как течение Прандтля – Майера. Вторая задача изучает
явление обтекания внутреннего угла и ранее рассматривалась как
плоский скачок уплотнения.
В дальнейшем параметры невозмущённого потока будут помече-
ны индексом «
∞
», параметры на верхней поверхности пластины – ин-
дексом «
в
», а на нижней поверхности – индексом «
н
».
Коэффициент равнодействующей аэродинамической силы, сов-
падающей в данном случае с нормальной силой, направлен перпенди-
кулярно к пластине и равен
2
2
∞∞
ρ
−
=
V
pp
С
вн
y
.
Принимая во внимание равенство
2
2
2
2
2
2
2
∞∞
∞
∞
∞
∞∞
∞∞
=
ρ
ρ
=
ρ kMp
a
p
kV
V
,
коэффициент нормальной силы можно определить по формуле
2
2
∞
∞∞
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
kM
p
p
p
p
C
в
н
y
. (57)
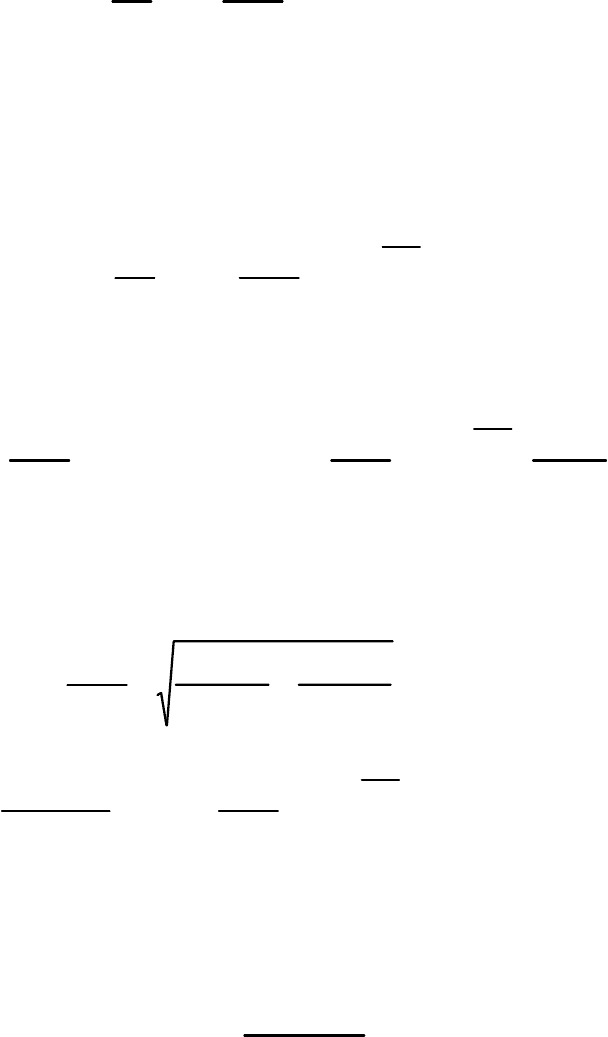
34
Здесь уменьшаемое есть безразмерное давление на нижней сто-
роне пластины (за скачком) и определяется по формуле (48):
()
1
1
2
1
2
2
−β
+
+=
∞
∞
М
k
k
p
p
н
.
Вычитаемое в правой части равенства (57) представляет собой
безразмерное давление на верхней стороне пластины (как при обтека-
нии выпуклого тупого угла), которое, согласно формуле (20), при
ϖ−=δ имеет вид
1
2
2
1
1
−
∞
∞
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
−
−=
k
k
в
M
k
p
p
.
Подставляя данные выражения в равенство (40), можно получить:
()
2
1
2
2
2
2
2
1
111
1
2
∞
−
∞∞
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
−
−−+−β
+
=
kM
M
k
M
k
k
C
k
k
y
.
Заменив первую круглую скобку согласно равенству (54), получа-
ем для коэффициента нормальной силы такую формулу:
()
⎪
⎩
⎪
⎨
⎧
+
ϖ
+
+
+
+
=
∞
2
2
2
1
2
1
2
1
M
kk
C
y
2
1
2
2
2
2
1
11
2
ϖ
⎪
⎭
⎪
⎬
⎫
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
ϖ
−
−−
ϖ
+
−
∞
∞
k
k
M
k
kM
. (58)
Если угол наклона пластины
ϖ равен или больше предельного уг-
ла поворота потока в течении Прандтля – Майера, который определя-
ется в соответствии с равенством (24)
()
∞
−
−=ϖ
Mk 1
2
,
то на верхней стороне пластины устанавливается полный вакуум. В
этом случае величина, стоящая в квадратных скобках выражения (58),
равна нулю.
При малых углах атаки коэффициенты подъёмной силы
ya
C и ло-
бового сопротивления
xa
C связаны с коэффициентом нормальной си-
лы следующим образом:
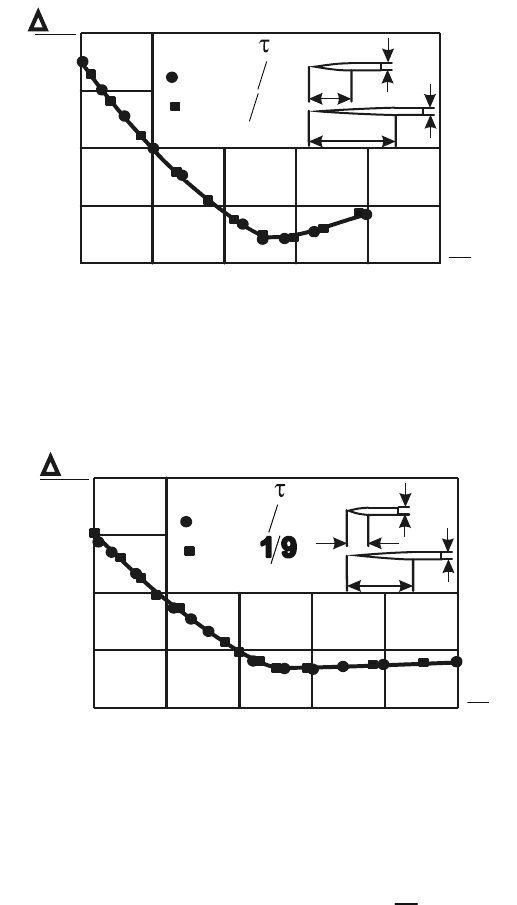
35
121
61
6
3
0
50
=
τ
.K
∞
M
L
d
L
x
02.
61.
21.
80.40.
20.
20.
−
40.
0
p
∞
p
d
L
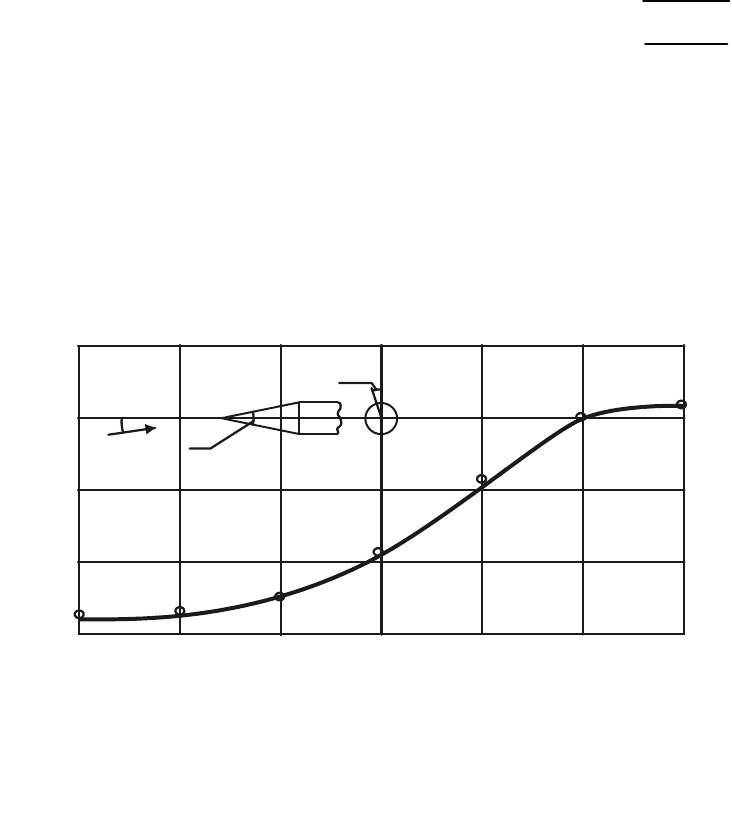
Рис. 10. Распределение давления
для первой пары тел
31
3
0
1
=
τ
K
∞
M
L
d
L
x
02.
61.
21.
80.40.
0
p
∞
p
d
L
9
80.80.
80
−
.80
−
.
61.
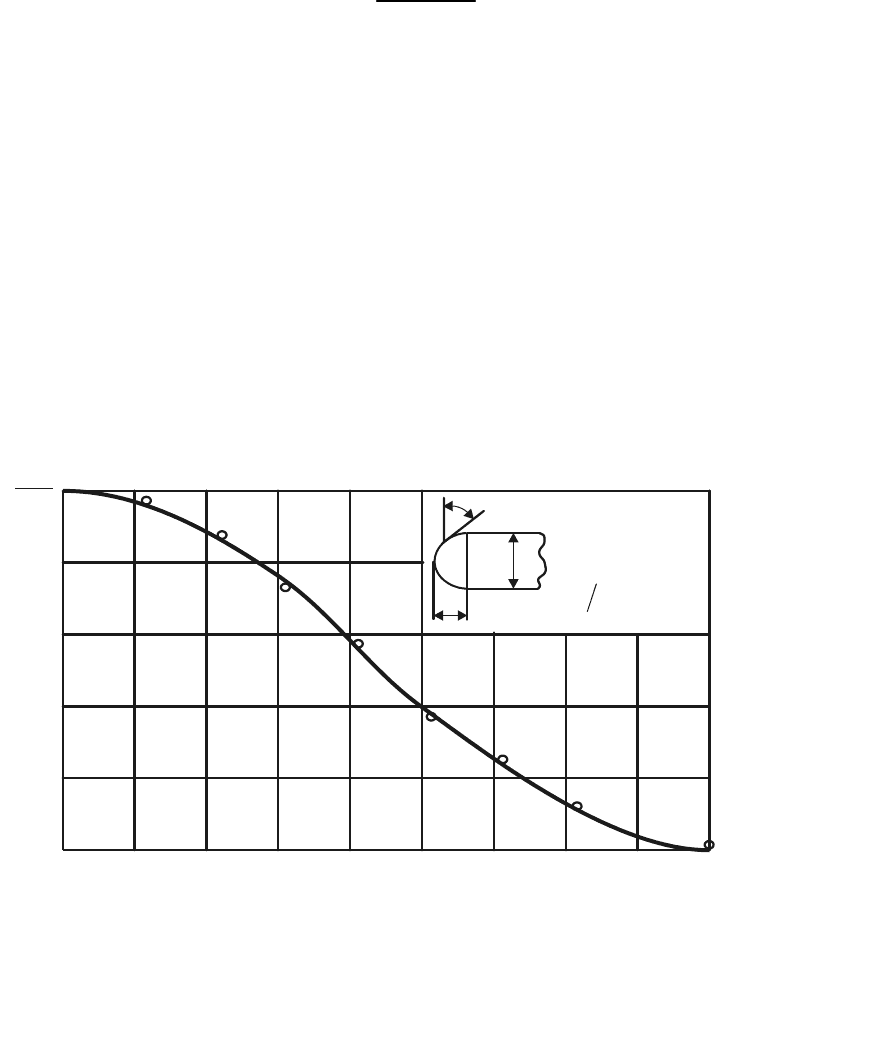
Рис. 11. Распределение давления
для второй пары тел
yyya
CcosCC ≈ϖ= , ϖ≈ϖ≈ϖ=
yayyxa
CCsinCC . (59)
При бесконечном увеличении числа Маха (
∞→
∞
M ) имеем
()
2
1 ϖ+= kC
ya
,
()
3
1 ϖ+= kC
xa
.
Как видим, аэродинамические коэффициенты при очень больших
значениях числа
∞
M и при малых углах атаки весьма малы и, кроме
того, зависят от величины
∞
M . В общем случае эти коэффициенты за-
висят от критерия
ϖ
K .
5. О ГИПЕРЗВУКОВОМ ОБТЕКАНИИ ТОНКИХ ЗАОСТРЁННЫХ
В ПЕРЕДНЕЙ ЧАСТИ ТЕЛ
Результаты, полученные
ранее, могут быть применены
непосредственно к расчёту
гиперзвукового обтекания
тонкого заострённого спереди
тела (рис. 10 - 12). Течение у
поверхности такого тела
представляет собой либо
течение за косым скачком
уплотнения (при положи-
тельном угле отклонения
потока), либо течение
Прандтля – Майера (при
отрицательном угле отклонения потока).
Как уже было показано
выше, в таких случаях при
малых углах заострения тела
и малых углах атаки основной
критерий подобия представ-
ляет собой произведение
числа Маха набегающего
потока
∞
M на некоторый
характерный угол
τ
. Под
величиной
τ
может
подразумеваться или угол
отклонения потока
ϖ=τ
(угол
наклона поверхности тела к
набегающему потоку), или относительная толщина тела
l
d
=τ
(отно-
шение наибольшего поперечного размера тела к его длине), так как в
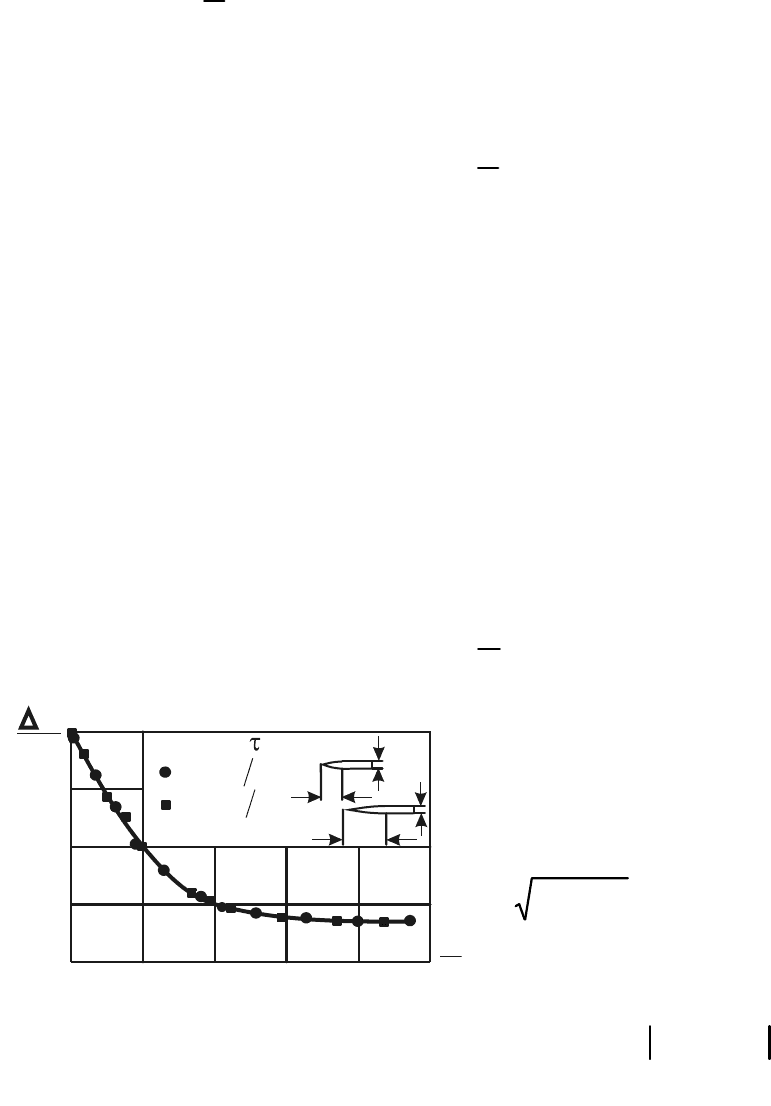
36
1
31
4
2
0
2
−
2
=
τ
K
∞
M
L
d
L
x
02 .
61.
21 .
80 .40.
0
p
∞
p
d
L
6
2
1
6
Рис. 12. Распределение давления
для третьей пары тел
случае тонкого тела эти величины пропорциональны. Тонкие заост-
рённые тела, у которых критерий
constMK =τ=
∞τ
, будем называть
аффинно-подобными. Очевидно, что сохранение такого аффинного
подобия обтекания тела при изменении угла атаки
α достигается в
том случае, когда последний пропорционален характерному углу тела,
т.е. при условии
const=
τ
α
. Итак, относительные величины скоростей,
коэффициенты сил аэродинамической природы и другие факторы, ко-
торые характеризуют гиперзвуковое обтекание тонкого тела, сохраня-
ют свои значения, если не изменяются величины
τ
∞
M
и
τ
α
.
Это подтверждается опытными данными, приведенными на
рис. 10 – 12, на которых изображены кривые значений безразмерного
избыточного давления на поверхности цилиндра с оживальной голов-
ной частью. Кривые получены при разных значениях числа Маха и для
различных величин относительной толщины оживальной части (при
нулевом угле атаки). Из рисунков видно, что кривые распре-
деления давления универсальны при изменении чисел
∞
M и
τ , если выдерживается условие аффинного подобия
constM =τ
∞
.
Исследования показывают, что область действия закона подобия
для гиперзвукового обтекания тонкого тела оживальной формы при-
близительно определяется следующими границами:
2>
∞
M ,
50,
l
d
<=τ
.
Область применимости за-
кона подобия значительно
расширяется, если в качестве
критерия подобия вместо ве-
личины
τ
∞
M взять величину
1
2
−τ
∞
M . Выше было пока-
зано, что при гиперзвуковом
обтекании тонкого тела про-
дольное возмущение скорости
ничтожно
∞
<< Vv
x
, а попе-
речная скорость пропорцио-
нальна углу наклона поверх-
ности тела:
∞
τ= Vv
y
.
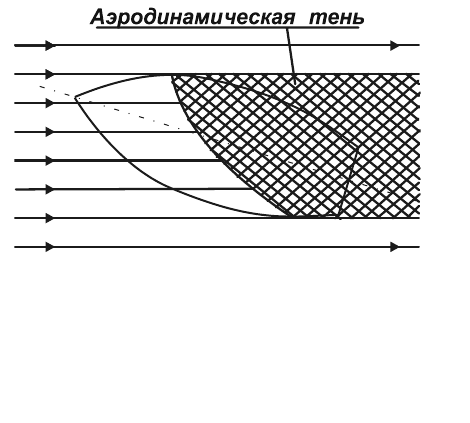
37
Рис. 13. Обтекание тела, соот-
ветствующее модели Ньютона
Иначе говоря, тонкое тело раздвигает слои обтекающего его газа
таким образом, как будто в каждом слое (независимо от соседних сло-
ёв) происходит вытеснение газа непроницаемым подвижным поршнем
в направлении, перпендикулярном направлению движения тела. Если
всю область обтекания разбить плоскостями, перпендикулярными к
скорости набегающего потока на множество слоёв, то в каждом из них
будет наблюдаться неустановившееся движение, направленное толь-
ко параллельно этим плоскостям.
Эта особенность гиперзвуковых течений получила название зако-
на плоских сечений. С помощью данного закона нетрудно рассчитать
лобовое сопротивление тела, определяемого работой расширения эк-
вивалентного поршня соответствующей формы. Работа совершается
над газом в слое за время прохождения тела сквозь этот слой. Контур
поршня в каждый момент времени и нормальную скорость его точек
определяем исходя из формы тела, а давление на его поверхности
находим из решения задачи о неустановившемся движении газа.
6. ЗАКОН СОПРОТИВЛЕНИЯ НЬЮТОНА
Накопленный значительный опыт показывает, что для расчёта со-
противления тела при гиперзвуковом обтекании можно использовать
закон сопротивления Ньютона, в математической модели которого по-
лагалось, что движущаяся жидкость состоит из одинаковых частиц, за-
полняющих равномерно пространство и не взаимодействующих друг с
другом. При столкновении с телом частицы газа теряют нормальную к
поверхности тела составляющую количества движения (происходит
неупругий удар), вследствие чего появляется сила давления потока на
тело. Избыточное давление газа на участки тела, расположенные по-
зади его наибольшего поперечного сечения, т.е. в аэродинамической
тени (рис. 13), Ньютон считал равным нулю.
Если элемент поверхности
тела площадью
dF наклонён к
невозмущённому набегающему
потоку под углом
ϖ , то масса
газа, в которой происходит
уменьшение количества
движения, равна
dFsinV ϖρ
∞
,
поэтому нормальная
составляющая силы давления
по закону Ньютона
определяется по выражению

38
dFsinVdP ⋅ϖρ=
∞
2
2
, (60)
а величина местного увеличения давления газа – по формуле
ϖρ==−
∞∞
2
2
sinV
dF
dP
pp . (61)
Коэффициент давления
p
C
определяется по следующей форму-
ле:
ϖ=
ρ
−
=
∞
∞
2
2
2
2
sin
V
pp
C
p
. (61
1
)
В общем случае обтекания тела предположение Ньютона, разу-
меется, не оправдывается в связи с тем, что возмущения, вызванные
телом в потоке, распространяются на большие расстояния от тела и
постепенно с удалением от тела ослабевают. Таким образом, сосед-
ние струйки газа имеют различные направления и величины скоро-
стей. Однако при обтекании тела с большой сверхзвуковой скоростью
закон Ньютона становится справедливым, так как в этом случае удар-
ная волна располагается близко к поверхности тела, и все струйки до
скачка уплотнения имеют одинаковое направление и величину скоро-
сти (невозмущённого потока). За скачком уплотнения упомянутые
струйки движутся в тонком слое между скачком и телом и приобретают
почти одинаковые скорости, параллельные поверхности тела. Чем
больше число Маха и тоньше тело, тем ближе к действительности
теория Ньютона. Вместе с тем, следует отметить, что даже в пре-
дельном случае при
∞→M закон Ньютона отвечает точному реше-
нию только при
1=
k
.
Если 1≠
k
, то закон Ньютона неточен даже при ∞→M , так как
при этом из точного решения (41) можно получить:
β
+
ρ=−
∞∞∞
2
2
1
2
sin
k
Vpp
; (62)
1
2
1
2
−
β
+
β
=ϖ
cos
k
tg
tg
. (63)
Однако практический расчёт распределения давления по по-
верхности тела, обтекаемого гиперзвуковым потоком, с помощью за-
кона Ньютона даёт во многих случаях удовлетворительные результа-
ты, несмотря на то, что влияние вязкости в теории Ньютона не учиты-
вается.
39
180
120
60
0
100.
C
p
10
°
76.
°
ϕ
°ϕ
96.
=
M
∞
300.
200.
Рис. 14. Распределение давления по поверхности
конуса, обтекаемого потоком под углом атаки.
Сравнение формулы Ньютона и
экспериментальных данных
На рис. 14 показано безразмерное давление
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
ρ
−
=
∞∞
∞
2
2
V
pp
С
p
в раз-
личных точках поперечного сечения конуса с центральным углом
°10
()
°=ϖ 5 . Конус обтекается потоком воздуха с числом Маха 96.M =
∞
под углом атаки
°=α 76. . Кривая на рис. 14 рассчитана по формуле
Ньютона (61
1
). Как видно из приведенного рисунка, эксперименталь-
ные точки лежат достаточно близко к теоретической кривой.
Пригодность формулы Ньютона для расчёта давления на теле
свидетельствует о том, что локальная картина обтекания определяет-
ся местным «углом встречи» поверхности тела с невозмущённым по-
током. Указанное обстоятельство привело к мысли о возможности рас-
чёта гиперзвукового обтекания заострённого тела по методу касатель-
ных клиньев (для осесимметричного тела – касательных конусов). В
этом методе предполагается, что местное давление в любой точке на
поверхности произвольного тела такое же, как на клине (конусе), каса-
тельном к поверхности в этой точке.
Метод касательных клиньев (конусов) менее удобен, чем формула
Ньютона, так как в общем случае зависимость давления на клине от
его угла представляется в неявном виде, а на конусе она определяет-
ся лишь численными методами.
Однако в гиперзвуковом приближении эти зависимости, как было
показано выше, удаётся получить в явной аналитической форме.
40
9060
30
0
L
d
80 .
60.
40 .
20.
C
C
*
p
p
50.dL
=
4M
=
ϖ
ϖ
Рис.15. Давление на поверхности обтекаемого в продольном
направлении цилиндра со сферической головной частью
Было замечено, что можно добиться значительно лучшего совпа-
дения расчётных и экспериментальных данных, если следующим об-
разом видоизменить формулу Ньютона:
∗
ϖ
ϖ
=
2
2
sin
sin
CC
*
pp
; (63
1
)
здесь
*
p
C – безразмерное давление в передней точке тела, которое
легко вычислить по теории сверхзвуковых течений идеального газа
при заданном
∗
ϖ – угле между касательной к контуру тела в этой точ-
ке и направлением набегающего потока;
ϖ – аналогичный угол в про-
извольной точке контура.
На рис. 15 показано распределение давления по поверхности
симметричного продольно-обтекаемого цилиндра со сферической го-
ловной частью при
4=
∞
М . Сплошная линия, рассчитанная по уточ-
нённой формуле Ньютона, проходит близко к экспериментальным точ-
кам.
Показанное на рис. 15 тело имеет затупленную носовую часть, и
при
ϖ =0 величина коэффициента давления равна
*
p
C . В месте сочле-
нения носовой и цилиндрической частей касательная к образующей
носовой части тела совпадает с образующей его цилиндрической час-
ти, поэтому в пределе коэффициент давления носовой части стремит-
ся к нулю.
