Тюрев В.В. Гиперзвуковые течения газа
Подождите немного. Документ загружается.


41
0
x
R
R
x
03.
02.01.
80.
40.
C
C
*
p
p
5.M
=
75.M
=
40
°
8
Рис. 16. Распределение давления по поверхности конуса со
сферической головной частью
На рис. 16 приведена картина распределения давления по длине
конуса со сферической головной частью радиуса
R
(центральный угол
раскрытия конуса
°=ϖ 802 ) при значениях числа Маха 8575 .,.M = .
Кривая, рассчитанная по формуле (63
1
), проходит близко к экспери-
ментальным точкам.
Необходимо отметить, что расчёты по формуле Ньютона дают хо-
рошие результаты для тел выпуклой формы. Для тел вогнутой формы
расчётные значения сил получаются заниженными. Это объясняется
тем, что в действительности слой газа, заключённый между скачком
уплотнения и поверхностью тела, не бесконечно тонок, поэтому при
криволинейной форме этого слоя возникает градиент давления по его
толщине. Разность давлений на поверхностях тела и скачка уплотне-
ния порождена центробежной силой, учитывая которую, можно полу-
чить поправку к формуле Ньютона, впервые введённую Буземаном.
С помощью формулы Ньютона удаётся решить задачу о форме
тела наименьшего сопротивления при некоторых заданных услови-
ях (при заданных объеме и длине тела или при заданных площади
наибольшего сечения и длине и т. д.).
Для решения такой задачи нужно, прежде всего, составить вы-
ражения для сил, действующих на тело.
Проекция элементарной силы давления на направление движения

42
– лобовое сопротивление – определяется согласно формуле (60):
dFsinVsindPdP
x
ϖρ=ϖ=
∞∞
3
2
,
откуда полная сила сопротивления
∫∫
ϖρ=ϖρ=
∞∞∞∞
y
F
y
F
x
dFsinVdFsinVP
2
2
3
2
. (64)
Здесь
F
– поверхность тела,
y
F
– ее проекция на плоскость, нор-
мальную к направлению движения.
Поперечная составляющая элементарной силы давления – подъ-
емная сила – определяется по формуле
dFcossinVdP
y
ϖϖρ−=
∞∞
2
2
.
Отсюда полная величина подъемной силы
∫∫
ϖϖρ−=ϖϖρ−=
∞∞∞∞
y
F
y
F
y
dFcossinVdFcossinVP
2
2
2
. (65)
Задаваясь той или иной формой зависимости угла наклона по-
верхности от длины, можно выполнить интегрирование выражений
(64) и (65) и получить аналитические зависимости, которые затем
использовать, в частности, для отыскания оптимальных значений
геометрических параметров тела при каких-либо заданных услови-
ях путем решения задачи на минимум величины
x
P
.
С помощью формулы Ньютона нетрудно, например, показать,
что при гиперзвуковом обтекании затупленный конус с меньшим боко-
вым углом может иметь меньшее сопротивление, чем заостренный
конус с большим углом.
Если «площадка» в носовой части затупленного конуса имеет ра-
диус
r
и его боковой угол
2
ϖ , а у «острого» конуса той же длины и
того же максимального радиуса
R
боковой угол
1
ϖ (рис. 17), то со-
гласно равенству (64) отношение сил лобового сопротивления этих
тел составляет величину
(
)
1
22
2
2222
1
2
ϖ
ϖ−+
==
sinR
sinrRr
P
P
f
x
x
,
где
22
2
1
2
x
R
R
sin
+
=ϖ
,
(
)
()
2
2
2
2
2
xrR
rR
sin
+−
−
=ϖ
.
Подставляя эти выражения и вводя безразмерные обозначения

43
r
R
2
ϖ
1
ϖ
V
∞
Рис. 17. Усеченный и
полный конусы равной
длины с одинаковыми
миделевыми
сечениями
Rxx = , Rrr = , окончательно получим
()
(
)
(
)
22
222
2
1
1
1
xr
xrr
xf
+−
+−
+=
.
Приравнивая нулю первую
производную функции f , найдем оп-
тимальную величину радиуса
опт
r ,
которому соответствует минимум
значения этой функции, т. е. минимум
сопротивления
422
250501 x.xx.r
опт
+−+= .
Например, при 1=x имеем 380.r
опт
=
и 760,f
min
= , поэтому сопротивление
оптимального усеченного конуса
оказывается на 24% меньше, чем у
обычного конуса той же длины.
Решая тем же методом эту задачу для клина, можно убе-
диться в том, что по расчету «оптимальный» усеченный клин по-
лучается лишь при 1<x
(
)
°>ϖ 45 , т. е. при столь большом цен-
тральном угле раскрытия, что, по-видимому, теряется практическая
значимость решения.
Рассмотрим упоминавшуюся ранее поправку Буземана к фор-
муле Ньютона для случая обтекания криволинейной поверхности.
Ввиду того, что слой газа, состоящий из частиц, заключенных между
поверхностью тела и ударной волной, не бесконечно тонок, давле-
ние непосредственно за волной при криволинейной траектории час-
тиц не равно давлению на поверхности; разность этих давлений вы-
звана действием центробежной силы.
В элементарном слое толщиной dS эта разность давлений, оче-
видно, равна
R
d
Vdp
δ
ρ=
2
,
где R – радиус кривизны слоя;
V,ρ – значения плотности газа и скорости движения в слое (вдоль
линии тока).
Из условия неразрывности имеем:
y
dFVVld
∞∞
ρ=δρ
.
Здесь
l
– ширина слоя по нормали к плоскости чертежа;

44
y
F – площадь сечения тела, плоскостью, нормальной к направ-
лению набегающего потока.
Подставляя значение δd из этого равенства в предыдущее,
имеем
y
VdF
l
R
V
dp
∞∞
ρ
=
.
После интегрирования получаем изменение давления поперек
слоя за счет центробежной силы:
∫
∞∞
∞
ρ
=−
y
F
y
VdF
lR
V
pp
.
Составляющая скорости, касательная к поверхности тела, при
встрече частиц с телом не изменяется, следовательно, ϖ=
∞
cosVV .
Радиус кривизны поверхности определяется по формуле
ββ
−=
ϖ
−=
dsinl
dF
d
ds
R
,
где s – длина, измеренная по обводу тела; β – угол встречи потока
с ударной волной.
Тогда разность давлений на стенке и на границе слоя опреде-
лится по формуле
∫
β
β
βρ=−
∞∞∞
y
F
y
dFcos
dF
d
sinVpp
2
.
Давление на границе слоя определяется по формуле Ньютона
(63
1
), поэтому избыточное давление на стенке с учетом центробежной
силы равно
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
β
β
β+βρ=−
∫
∞∞∞
y
F
y
dFcos
dF
d
sinsinVpp
2
2
. (66)
Эта зависимость впервые была получена Буземаном и названа
формулой Ньютона – Буземана. Для тел выпуклой формы расчёт по
исходному закону Ньютона (61) дает результаты, более близкие к
опытным данным, чем расчет по уточненной формуле (66). Это объ-
ясняется тем, что по формуле Ньютона давление получается ниже
истинного (так как угол встречи потока с ударной волной β больше
угла встречи с телом ϖ , который фигурирует в формуле Ньюто-
на), а для выпуклого тела поправка на центробежную силу дополни-
тельно уменьшает давление. Наоборот, в случае обтекания вогнутого

45
тела поправка на центробежную силу положительна, т. е. компенси-
рует заниженное давление, которое дает закон Ньютона. Сопостав-
ление расчетов с опытными данными показывает, что для вогнутого
тела формула (66) дает лучшие результаты, чем формула (61).
7. ВЛИЯНИЕ МАЛОГО ЗАТУПЛЕНИЯ ПЕРЕДНЕГО КОНЦА
ТОНКОГО ТЕЛА НА ЕГО ОБТЕКАНИЕ ПРИ ГИПЕРЗВУКОВЫХ
СКОРОСТЯХ
При гиперзвуковом обтекании тонкого тела с затупленной носо-
вой частью образуется отошедший скачок уплотнения, в передней
части которого давление возрастает настолько сильно, что даже при
малых размерах затупления аэродинамическое сопротивление мо-
жет существенно увеличиться. Мимо этого факта нельзя пройти в
связи с тем, что реальные тела (крылья, фюзеляжи, корпуса ракет)
всегда бывают затуплены. Осуществить полет идеально заострен-
ного тела нельзя хотя бы потому, что при больших скоростях поле-
та нагревание воздуха около носовой части тела настолько значи-
тельно, что заостренный конец неизбежно должен оплавиться.
Положим в первом приближении, что сопротивление затупленного
тонкого тела равно сумме сопротивления затуплённой части
1x
P и
сопротивления остальной части тела
2x
P , давление на которую
рассчитываем, исходя из теории гиперзвукового обтекания заост-
ренного тела (см. разд. 5). Отношение этих сопротивлений опреде-
ляют в соответствии с равенствами (41), (47) и (55):
2
2
1
2
1
y
y
x
x
F
F
P
P
ϖ
≈
. (67)
Здесь ϖ – угол между боковой поверхностью тела и направлением
набегающего потока;
1y
F ,
2y
F – проекции поверхностей соот-
ветственно затупленной части и всего остального тела на плос-
кость, перпендикулярную к направлению набегающего потока.
Отсюда видно, что дополнительное сопротивление, вызванное за-
туплением тонкого тела, сравнимо с сопротивлением исходного за-
остренного тела при весьма малой относительной площади затупле-
ния:
2
2
1
ϖ≈
y
y
F
F
. (68)
Например, при угле отклонения потока рад.08705 =°=ϖ сопротив-
ление затупленного тела при относительной площади затупления

46
≈
2
1
y
y
F
F
0,0075 примерно удваивается. Заменим отношение площадей
отношением линейных размеров
ν
⎟
⎠
⎞
⎜
⎝
⎛
=
D
d
F
F
y
y
2
1
.
Здесь d – поперечный размер затупленной части;
LD ϖ= – линейный размер максимального поперечного сечения
тела;
L – длина тела;
ν – показатель степени, равный единице для плоских тел и
двум для осесимметричных тел.
Таким образом, имеем для клина
D
d
F
F
y
y
=
2
1
,
а для конуса
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
=
D
d
F
F
y
y
.
Относительный линейный размер затупленной части тонкого те-
ла, у которого сопротивление при гиперзвуковом обтекании в два
раза больше, чем у такого же заостренного тела, связан с углом
отклонения потока соотношением
3
2
ϖ≈
D
d
или
ν
ν+
ϖ≈
2
L
d
.
В рассмотренном выше примере ( 0870.=ϖ радиана) относитель-
ные размеры затупления у клина
00750
2
.Dd ≈ϖ≈
, у конуса
0870.Dd ≈ .
Детальное рассмотрение задачи о гиперзвуковом обтекании
тонкого тела показывает, что затупление носовой части тела вызывает
существенное искажение картины распределения давлений на значи-
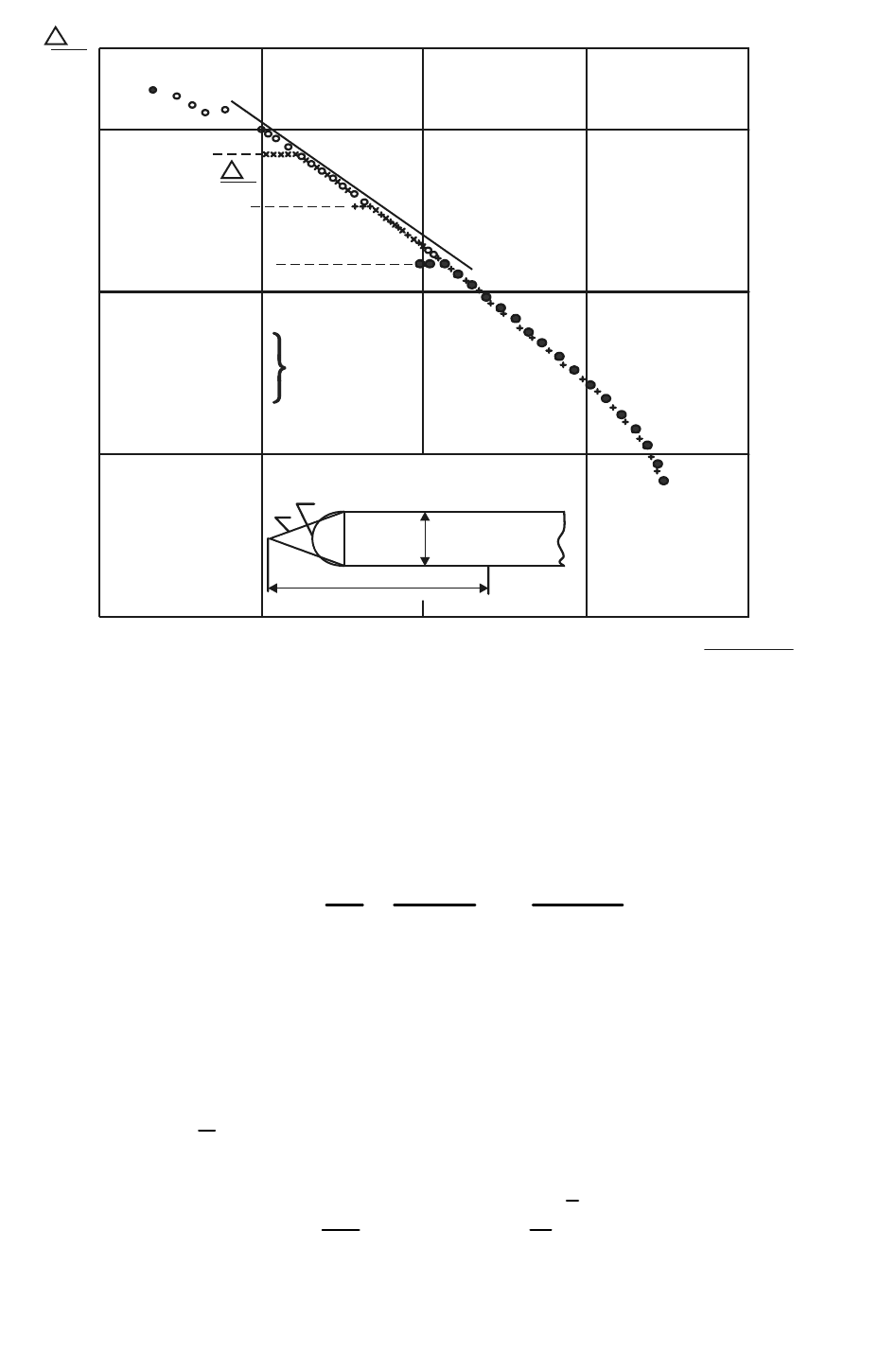
тельной части боковой поверхности тела. На рис. 18 показано распре-
деление безразмерного избыточного давления по длине пластины с
клиновидной и полукруглой передними кромками. Угол раскрытия
переднего клина подбирался для каждого значения числа Маха в
набегающем потоке (
∞
M
= 5,00; 6,86; 9,50) так, чтобы скорость за
головным присоединенным скачком равнялась скорости звука
(
1
M
=1), а пластина с полукруглой кромкой испытывалась при
∞
M
=
14.
47
x
d
контура
излома
точки
.2141
.3761
.0014
.509
.866
.005
.3261
2
1
10
1
dMC
x
x
3
10
1
−
10
2
−
10
3
−
10
4
−
10
1
−
p
p
∞
p
p
∞
1
2
M
C
x
.400
1
З
у
Значения
Рис. 18. Распределение давления на пластинке с клиновид-
ной (1) и закруглённой (2) кромками
Безразмерные кривые
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
=
∞
∞
∞
dMC
x
f
p
pp
p
p
x
3
∆
отходят от некоторой универсальной зависимости лишь вблизи точки
излома контура; значение величины
x
C для носовой части тела
клиновидной формы (рис.18) определялось по теории косого скачка
уплотнения, а для полукруглой формы — по уточненной формуле
Ньютона
⎟
⎠
⎞
⎜
⎝
⎛
=
∗
pC
x
3
2
. Расчетная зависимость (сплошная линия)
3
2
3
120
⎟
⎠
⎞
⎜
⎝
⎛
=
∞
x
d
MC.
p
p
x
∆
удовлетворительно согласуется с экспериментальными данными.
Эта приближенная зависимость получена с помощью теории то-
48
0
02.
51.
01.
50.
2
2
tg
d
x
C
x
50.
01.
51.
22
tgV
p
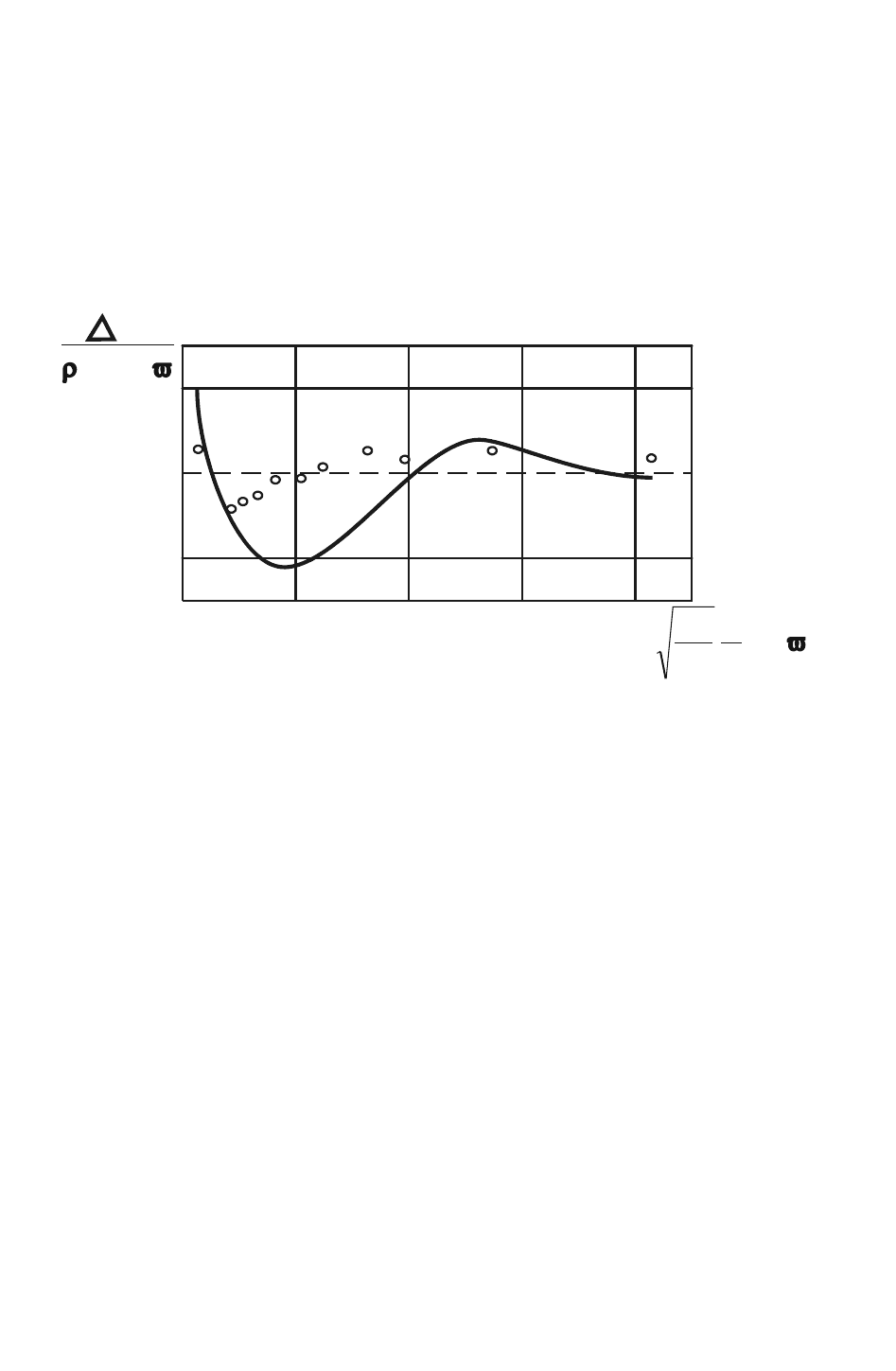
Рис. 19. Давление на поверхности затупленного конуса
чечного взрыва и гипотезы плоских сечений, причем сила, дейст-
вующая на затупленный носок тела, рассматривается как дополни-
тельная сосредоточенная сила.
В заключение отметим одну интересную особенность обтекания
тонкого затупленного конуса, обнаруженную и теоретическим, и экс-
периментальным путем. Указанная особенность состоит в том, что из-
быточное давление (рис. 19) на части поверхности затупленного кону-
са оказывается ниже, чем у заостренного конуса.
Иначе говоря, воздействие обтекания затупленного носка на со-
седние области потока может привести к тому, что при известной
«степени затупленности» конуса его сопротивление окажется ниже,
чем у остроносого. На рис. 19 сплошная кривая получена в результате
расчётов. Здесь же для сравнения приведена кривая распределения
давления по образующей остроносого конуса (пунктир).
8. О ВЛИЯНИИ ВЯЗКОСТИ В ГИПЕРЗВУКОВЫХ ТЕЧЕНИЯХ
Влияние вязкости в гиперзвуковых течениях представляет собой
сложную проблему. Все газы и жидкости являются вязкими и тепло-
проводными, однако воздух и другие газы – это маловязкие и слабо-
теплопроводные среды, и для них внутреннее трение и теплопровод-
ность в основном проявляются в тонких слоях, примыкающих к гра-
ничной поверхности обтекаемого тела. Вследствие этого для реше-
ния многих практически важных задач обтекания тел потоком газа с
большими скоростями можно воспользоваться идеями и методами
теории пограничного слоя. Впервые они были выдвинуты Л. Прандт-
лем для случая течения несжимаемой жидкости ещё в 1904 г. В тех
случаях, когда пограничный слой намного тоньше ударного слоя (зо-
49
С
к
а
ч
о
к
слоягопогранично
границаВнешняя
т
о
к
а
Л
и
н
и
я
x
TVp
T
V
p
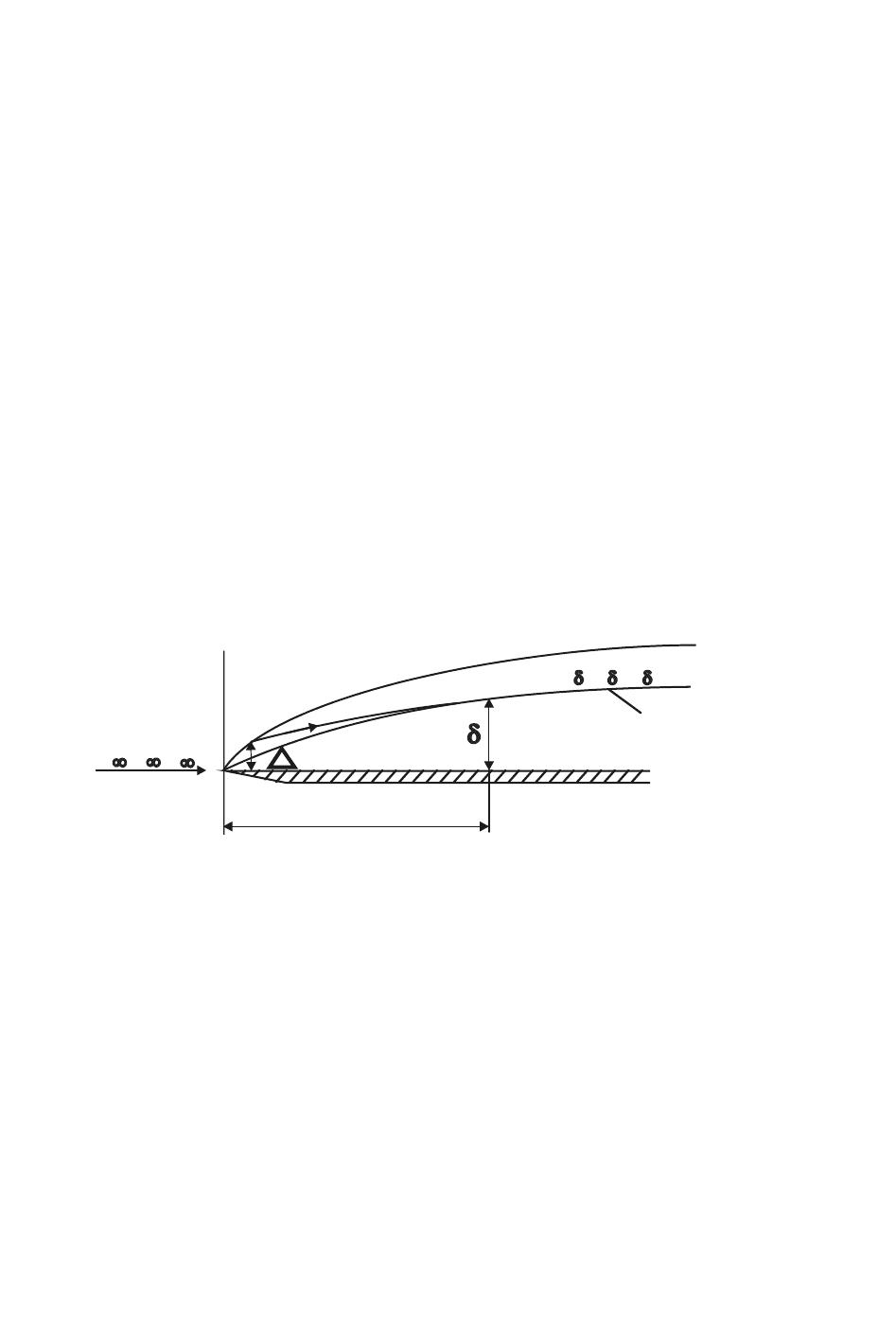
Рис. 20. Схема пограничного слоя и
индуцированного им ударного слоя
ны между ударной волной и поверхностью тела), расчет напряжений
трения и теплообмена ведется обычными методами, разработанными в
теории пограничного слоя.
Правда, при гиперзвуковых скоростях температура газа вследст-
вие торможения потока на скачках уплотнения и в пограничном слое
может оказаться очень высокой и тогда придется учитывать не только
сжимаемость газа, но также диссоциацию, а при температурах выше
°5000 и ионизацию газа. Кроме того, в гиперзвуковом пограничном
слое при обтекании остроносого тонкого тела, или даже постав-
ленной по потоку плоской пластины, появляется продольный гради-
ент давления, ибо, как известно, пограничный слой воздействует на
внешний поток так же, как утолщение тела (на величину толщины вы-
теснения пограничного слоя), вызывая образование ударных волн
(рис. 20). Иначе говоря, пограничный слой может породить во внеш-
нем потоке у остроносого тела «собственный» ударный слой, начи-
нающийся от передней кромки тела. При обтекании тела с затуп-
ленным носком обычно этого не наблюдают, в связи с тем, что в по-
граничном слое за отошедшей ударной волной скорости бывают доз-
вуковыми или ненамного превосходят скорость звука.
Теоретическое и экспериментальное исследования гиперзвукового
пограничного слоя, вызывающего на пластине и на тонком теле (клин,
конус) появление ударного слоя с продольным градиентом давлений,
проводились в работах Беккера, Лиза и Пробстина, Бертрама, Кен-
далла и др. [18].
Суть теоретического подхода к решению этой задачи состоит в
следующем. Давление в каждом поперечном сечении пограничного
слоя считается постоянным и зависящим от полного угла поворота
потока:
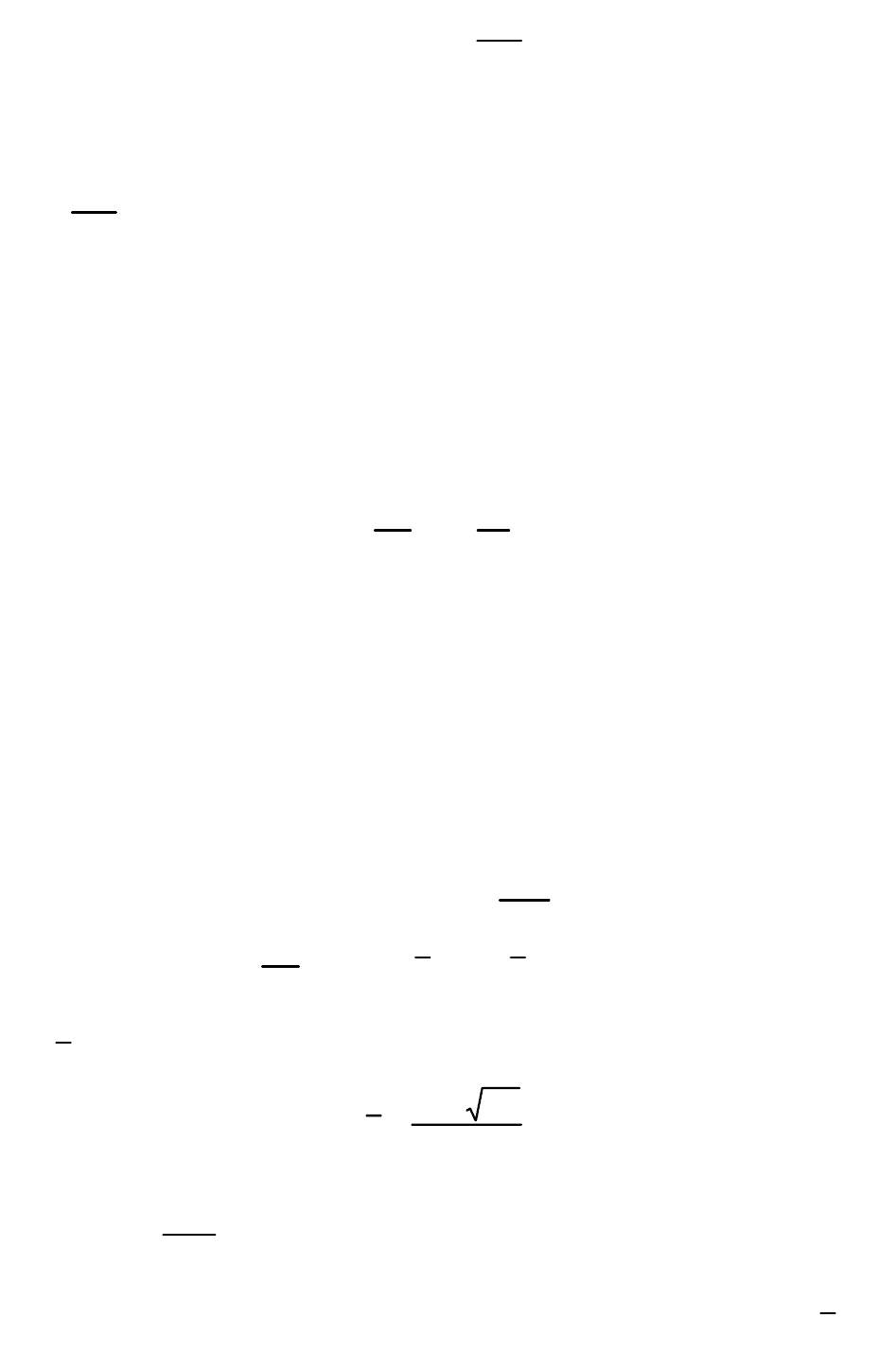
50
dx
d
∗
δ
+ϖ=ϖ
0
.
Здесь
0
ϖ – местный угол отклонения поверхности тела от направ-
ления невозмущенного потока;
dx
d
∗
δ
=ϖ∆
– дополнительное отклонение потока, соответствующее
толщине вытеснения
∗
δ пограничного слоя (ввиду малости углов тан-
генс угла считаем равным самому углу, измеренному в радианах).
Величину
∗
δ можно определить приближенно, используя из-
вестные методы расчета пограничного слоя без градиента давления.
При вычислении толщины
∗
δ давление принимается в первом при-
ближении таким же, как в потоке без пограничного слоя. Зависимость
вязкости от температуры аппроксимируется линейной функцией
δ
∞
δ
ϖ
=
µ
µ
Т
Т
с
r
,
где индекс «
r
» относится к значениям на стенке, а индекс «δ » –
к границе слоя.
В свою очередь, изменение давления, вызванное отклонением
внешнего потока под воздействием тела увеличенной вследствие
нарастания пограничного слоя толщины, можно вычислить с помощью
уточненной формулы Ньютона (61) или по методу касательных
клиньев или конусов.
В итоге, например, для плоской пластины получается следующая
приближенная формула для безразмерного давления в ламинарном
пограничном слое (при 41.
k
= и
7250 .
C
Pr
p
=
λ
µ
=
):
2
0503101 χ+χ+=
∞
..
p
p
, (69)
где χ – фактор взаимодействия слоя с потоком:
∞
∞∞
=χ
ex
R
СМ
3
.
Здесь индекс
∞
соответствует параметрам невозмущенного по-
тока,
∞
∞
∞
ν
=
xV
R
ex
– число Рейнольдса.
Сравнение расчетных данных с экспериментальными, приве-
денное на рис. 21, дает удовлетворительные результаты при
4≤χ
.
Числа Рейнольдса, вычисленные по толщине передней кромки
