Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие

Подождите немного. Документ загружается.

Глава 7. Основы выборочного метода

В этой главе рассмотрим вопросы построения оценок случайных величин

по выборочным данным и показатели качества этих оценок.

7.1. Общие сведения о выборочном методе

В практике статистических наблюдений различают два вида наблюдений:

сплошное, когда изучаются все объекты, и выборочное, когда изучается часть

объектов. Вся подлежащая изучению совокупность объектов называется гене-

ральной совокупностью.

Генеральная совокупность – весь мыслимый набор данных, описывающих

какое-либо явление. Более строго: генеральная совокупность – это случайная

величина ξ(ω), заданная на пространстве

элементарных событий Ω с выделен-

ным в нем полем событий S, для которых указаны их вероятности P. Понятие

генеральной совокупности в определенном смысле аналогично понятию слу-

чайной величины (закону распределения вероятностей).

Выборка из объема n (или просто выборка) – ограниченный набор n реаль-

но наблюдаемых выборочных из генеральной совокупности значений, описы-

вающих

исследуемое явление.

Конкретная выборка x

, … , x

– это конечная последовательность n чисел

– реализация случайной величины ξ(ω).

ие

Случайная выборка объема n из генеральной совокупности (или выборка из

распределения случайной величины ξ) – это последовательность X

, … , X

не-

зависимых одинаково распределенных случайных величин, распределение ка-

ждой из которых совпадает с распределением случайной величины ξ(ω).

Случайная выборка имеет распределен

{}{}

∏∏

=<=<<=

iinnnXX

xFxXPxXxXPxxF

111,...,

)(,...,),...,(

Суть выборочного метода состоит в том, чтобы по некоторой части ге-

неральной совокупности (по выборке) делать выводы о ее свойствах в целом.

Преимущества выборочного метода наблюдения по сравнению со сплошным:

- существенно экономит затраты ресурсов;

- является единственно возможным в случае бесконечной генеральной сово-

купности;

- при тех же затратах ресурсов дает

возможность проведения углубленного

анализа за счет расширения программы исследования;

- позволяет снизить ошибки регистрации, т.е. расхождения между истинным

и зарегистрированным значениями признака.

Основной недостаток выборочного метода – ошибки репрезентативности.

Выборка называется репрезентативной (или представительной), если она

достаточно хорошо воспроизводит генеральную совокупность.

Чтобы по данным выборки иметь возможность судить о генеральной сово

купности, она должна быть отобрана случайно.

7.2. Вариационные ряды и их характеристики

7.2.1. Вариационные ряды и их графическое изображение

Различные значения признака (случайной величины ξ) называются вари-

антами, обозначим как x. Для того чтобы рассмотреть и проанализировать ис-

ходные данные, их необходимо каким-то образом представить. Основные фор-

мы представления выборки из генеральной совокупности следующие.

Представление выборки в несгруппированном виде

),...,(

1 n

Представление выборки в упорядоченном виде

)()2()1(

...

xxx ≤≤

≤

. В этом

случае x

(i)

− i-й член вариационного ряда (или i-я порядковая статистика). Чле-

ны вариационного ряда, в отличие от элементов исходной выборки, уже не яв-

ляются взаимно независимыми (из-за предварительной упорядоченности).

Представление выборки в группированном виде. Здесь область задания

случайной величины ξ разбивается на L интервалов группировки. При этом из-

вестны только количество элементов выборки

)...,,1(, Lin

, попавших в i-й ин-

тервал, и последовательность границ интервалов разбиения. Область задания

случайной величины ξ, как правило, ограничена минимумом и максимумом

выборки. Согласно формуле Старджесса рекомендуемое число L интервалов

[]

nL lg322,31 += ,

а величина интервала равна

Lxxh )(

minmax

−

, где

minmax

−

− разность между

наибольшим и наименьшим значениями признака. Иногда интервалы группи-

ровки могут быть неравными. Это определяется условиями проведения экспе-

римента и природой исследуемого явления.

Числа, показывающие, сколько раз встречаются варианты из данного ин-

тервала, называются частотами

)...,,1(, Lin

, а отношения − отно-

сительными частотами (или частостями).

nnw

Следует помнить, что от несгруппированной выборки всегда можно перей-

ти к группированной, но не наоборот. Переход к группированной форме со-

пряжен с потерей информации об исследуемом явлении.

Определение 7.1. Вариационный ряд – это ранжированный в порядке воз-

растания или убывания ряд вариантов с соответствующими им частотами.

Вариационный ряд может быть дискретным или непрерывным. Вариаци-

онные ряды графически могут быть изображены в виде полигона, гистограммы

и кумулятивной кривой.

Полигон служит для изображения, как правило, дискретного вариационно-

го ряда и представляет собой

ломанную, у которой концы отрезков имеют ко-

ординаты

Linx

...,,1),,( =

Гистограмма используется только для изображения интервальных вариа-

ционных рядов и представляет собой ступенчатую фигуру из прямоугольников

с основаниями, равными интервалам значений признака

, и высота-

iii

xxh −=

ми, равными относительным частотам w

каждого из интервалов. Если соеди-

нить середины верхних оснований прямоугольников отрезками, то можно по-

лучить полигон того же распределения.

Кумулятивная кривая (кумулянта) – кривая накопленных частот (часто-

стей). Для дискретного ряда кумулянта представляет собой ломанную, соеди-

няющую точки

или , где . Для

интервального ряда ломаная начинается из точки, абсцисса которой равна на-

чалу первого интервала, а ордината – накопленной частоте (частости), равной

нулю. Другие концы этой ломанной соответствуют концам интервалов.

),(

Liwx

K1),,( =

∑∑

wwnn

К характеристикам одномерного распределения частот относятся:

- меры положения, характеризующие среднее положение распределения;

- меры рассеяния, отражающие изменчивость распределения;

- меры формы, характеризующие

отклонение распределения от нормального.

7.2.2. Средние величины

Средние величины характеризуют значения признака, вокруг которого

концентрируются наблюдения. Наиболее распространенной из средних величин

является средняя арифметическая.

Определение 7.2. Средняя арифметическая вариационного ряда – сумма

произведений всех вариантов на соответствующие частоты, деленная на сумму

частот:

∑

где

− варианты дискретного ряда или середины интервалов интервального

вариационного ряда,

− соответствующие им частоты.

Основные свойства средней арифметической аналогичны свойствам мате-

матического ожидания:

1. Средняя арифметическая константы равно этой константе,

cc = .

ccx = .

+=+ .

4. Средняя арифметическая отклонений вариантов от средней арифметической

равна нулю:

−

5. Средняя арифметическая суммы признаков равно сумме средних арифмети-

ческих этих признаков:

yxyx +=+

6. Общая средняя равна средней арифметической групповых средних, причем

весами являются объемы групп:

∑

, где

− групповая средняя j-й

группы, объем которой равен

, L − число групп.

Замечание 7.1. Можно показать, что средняя арифметическая – это оценка

математического ожидания на основе метода наименьших квадратов.

При решении практических задач могут использоваться и иные формы

средней, которые получаются из средней степенной

k-го порядка:

0,,

)(

>∈

⎟

⎠

⎞

⎜

⎝

⎛

∑

xZk

x .

Очевидно, что при k = 1 имеем формулу средней арифметической. При некото-

рых других значениях k получаем формулы:

∑

−

=−=

)1(

− средняя гармоническая;

xxk

∏

)0(

− средняя геометрическая.

Рассмотренные выше средние величины называют аналитическими. Наря-

ду с ними в статистике применяют структурные или порядковые средние, наи-

более распространенными из которых являются медиана и мода.

Медианой вариационного ряда называется значение признака, приходящее-

ся на середину упорядоченного по возрастанию ряда наблюдений. Если выбор-

ка состоит из (2

N + 1) членов, то под медианой понимается (N + 1) -е по вели-

чине значение варианты. Если же выборка состоит из 2N членов, то медианой

считают полусумму N-го и (N + 1)-го значений варианты.

Достоинство медианы как меры положения заключается в том, что на нее

практически не влияют значения крайних членов вариационного ряда

, особен-

но, когда они оказались чрезмерно большими по абсолютной величине в срав-

нении с остальными членами ряда.

Модой вариационного ряда называется вариант, которому соответствует

наибольшая частота. Особенность моды как меры положения состоит в том, что

она не изменяется при изменении членов ряда, отдаленных от центра ряда.

7.2.3. Показатели вариации и формы распределения

Средние величины не отражают изменчивости, степени рассеяния значе-

ний признака. Для оценки меры рассеяния используют показатели вариации.

Простейшей и весьма приближенной мерой рассеяния является вариацион-

ный размах R, равный разности между наибольшим и наименьшим вариантами

ряда:

minmax

xxR −=

Если выборка состоит только из двух значений, то вариационный размах

является исчерпывающей характеристикой рассеяния. При увеличении объема

выборки эта мера уже становится недостаточной, потому что учитывает только

два крайних, экстремальных значения.

Разделим вариационный ряд девятью значениями на десять равных частей.

Эти значения назовем децилями и обозначим

. Мерой рассеяния

(которая, в противоположность вариационному размаху, почти не зависит от

экстремальных значений и в то же время включает в себя 80% всего выбороч-

ного распределения и имеет очень малые колебания от выборки к выборке) яв-

ляется интердецильный размах, равный

,..., DZDZ

1980

DZDZI

−

Наибольший интерес представляют меры рассеяния наблюдений вокруг

средних величин, в частности, вокруг средней арифметической.

Определение 7.3. Средним линейным отклонением вариационного ряда на-

зывается средняя арифметическая абсолютных величин отклонений вариантов

от их средней арифметической:

nxx

∑

−

Определение 7.4. Дисперсией s

вариационного ряда называется средняя

арифметическая квадратов отклонений вариантов от их средней арифметиче-

ской:

nxx

∑

−

)(

В качестве меры рассеяния, наряду с выборочной дисперсией, используют

среднее квадратическое отклонение s, равное

ss = .

Введенные выше меры рассеяния являются размерными величинами. По-

этому могут возникнуть трудности при их сравнении для выборок из разных

генеральных совокупностей. Наиболее распространенной безразмерной меры

рассеяния является коэффициент вариации v, равный

)0(%,100 ≠⋅= x

v .

Выборка является однородной, если

. Коэффициент вариации особенно

пригоден для сравнения выборок из генеральных совокупностей одного типа,

т.е. имеющих один и тот же тип закона распределения.

%33>v

Начальный момент v

и центральный момент µ

k-го порядка вариационно-

го ряда определяются по формулам

∑

nxx

∑

−

=µ

)(

С помощью моментов распределения можно описать не только среднюю

тенденцию и рассеяние, но и другие особенности вариации признака, в частно-

сти форму распределения. Как было указано в § 3.4, форму распределения ха-

рактеризуют коэффициенты асимметрии и эксцесса. Данные коэффициенты

определяют через центральные моменты.

Замечание 7.2. Средняя арифметическая, дисперсия и другие рассмотрен-

ные характеристики вариационного ряда являются статистическими аналогами

математического ожидания ][

, дисперсии ][

D и соответствующих харак-

теристик случайной величины ξ.

7.3. Понятие оценки параметров

Сформулируем задачу оценки параметров в общем виде. Пусть распреде-

ление признака ξ – генеральной совокупности – задается функцией вероятно-

стей

)(),(

xPxp =

=θ

(для дискретной случайной величины ξ) или плотно-

стью вероятности

(для непрерывной случайной величины ξ), которая

содержит неизвестный параметр θ. Например, это параметр λ для показатель-

ного распределения, a и σ

),( θ

для нормального распределения и т.д. Параметр θ

является величиной неслучайной, детерминированной.

Для вычисления параметра θ исследовать всю генеральную совокупность

не представляется возможным. Поэтому о параметре θ судят по выборке, со-

стоящей из значений x

, … , x

. Эти значения можно рассматривать как частные

значения n независимых случайных величин X

, … , X

, каждая из которых име-

ет тот же закон распределения, что и сама случайная величина θ.

Определение 7.5. Оценкой

)

параметра θ называют всякую функцию ре-

зультатов наблюдений над случайной величиной ξ, с помощью которой судят о

значении параметра θ:

),...,(

1 nnn

XXθ=θ

)

Т.к. X

, … , X

− случайные величины, то и оценка

)

− случайная величи-

на, зависящая от закона распределения случайной величины θ и числа n.

Всегда существует множество функций от результатов наблюдений

, … , X

, которые будут оценками параметра θ. Возникает проблема – как из-

мерить «близость» оценки

)

к истинному значению θ, или как определить ка-

чество оценки? Качество оценки определяется не по одной конкретной выбор-

ке, а по всему мыслимому набору конкретных выборок, т.е. по случайной вы-

борке. Поэтому для установления качества полученных оценок следует в соот-

ветствующих формулах заменить конкретные выборочные значения x

на слу-

чайные выборочные значения X

Качество оценки устанавливают, проверяя, выполняются ли следующие

три свойства: состоятельность, несмещенность и эффективность.

Определение 7.6. Оценка

)

называется состоятельной, если она сходится

по вероятности к истинному значению θ:

(

)

1lim0 =ε<θ−θ>ε∀

∞→

)

, или

θ→θ

∞→

)

. (7.1)

Свойство состоятельности является обязательным для оценки.

Определение 7.7. Оценка

)

называется несмещенной, если ее математиче-

ское ожидание равно истинному значению θ:

θ=θ ][

)

. (7.2)

Данное свойство желательно, но не обязательно. Часто полученная оценка

бывает смещенной, но ее можно скорректировать так, чтобы она стала несме-

щенной. Иногда оценка бывает смещенной, но асимптотически несмещенной,

что означает:

θ=θ

∞→

][lim

)

Определение 7.8. Оценка

∗

)

называется эффективной в определенном

классе оценок Θ, если она самая точная среди всех оценок этого класса, т.е.

имеет минимальную дисперсию:

][min][

θ=θ

Θ∈θ

∗

)

. (7.3)

Эффективность является решающим свойством, определяющим качество

оценки. Эффективность оценки

)

определяется отношением:

][

)(

=θ

∗

)

. (7.4)

Чем ближе e к 1, тем эффективнее оценка. Если

при , то такая

оценка называется

асимптотически эффективной. На практике в целях упро-

щения расчетов часто делается компромисс между несмещенностью и эффек-

тивностью – используют незначительно смещеннные оценки или оценки, обла-

дающие большей дисперсией

1→e

∞→n

][

D θ

)

по сравнению с эффективными оценками.

Ниже рассмотрим, какими из свойств обладают некоторые полученные

выше оценки числовых характеристик.

7.3.1. Среднее арифметическое выборочных значений как оценка ма-

тематического ожидания

Пусть случайная величина ξ имеет математическое ожидание и дисперсию,

равные соответственно a и σ

. Для случайной выборки оценка математического

ожидания примет вид:

∑

)

. Согласно следствию 5.1 aX

n ∞→

→ , что

означает состоятельность оценки

)

. Несмещенность оценки

)

устанав-

ливается прямой проверкой:

MaM

===

⎥

⎦

⎤

⎢

⎣

⎡

∑∑∑

==− 111

][

)

Теперь докажем, что

)

эффективна в классе линейных несмещенных оце-

нок. Линейная оценка имеет вид

∑

iin

Xca

)

. (7.5)

Для линейной несмещенной оценки выполняется условие

aaM

=][

)

, поэтому

∑∑∑

===

⎥

⎦

⎤

⎢

⎣

⎡

iin

caXMcXcMaM

111

][][

)

т.е. для ее несмещенности необходимо

. Найдем дисперсию

∑

∑∑∑

===

σ==

⎥

⎦

⎤

⎢

⎣

⎡

iin

cXDcXcDaD

][][

)

Поэтому для определения наиболее эффективной в классе линейных несме-

щенных оценок надо минимизировать дисперсию

][

)

при выполнении усло-

вия несмещенности

∑

ccc

minarg),,( K . (7.6)

Задача (7.6) – задача на условный экстремум, которая сводится к задаче на

безусловный экстремум. Строим для (7.6) функцию Лагранжа:

⎟

⎠

⎞

⎜

⎝

⎛

−λ−=λ

∑∑

1),,,(

ccccL K .

Для определения точки экстремума находим частные производные и приравни-

ваем их к нулю:

=−=

λ∂

∂

∑

;

nic

,...,1,02 ==λ−=

∂

Подставляя значения

),...,1(,2/ nic

λ=

, полученные из первых n уравнений,

в последнее уравнение, получаем

nic

,...,1,

=⇒=

Итак, при

),...,1(,/1 ninc

, оценка (7.5) имеет минимальную дисперсию,

т.е.

)

является эффективной в классе линейных несмещенных оценок.

7.3.2. Свойства оценки дисперсии

Для случайной выборки оценка дисперсии примет вид

∑

−=σ

)(

)

. (7.7)

Изучение свойств этой оценки начнем с проверки на несмещенность. Рас-

крыв квадрат под знаком суммы в уравнении (7.7), имеем:

(

)

∑

+−=σ

iin

XMXXMXM

][][2][

][

)

. (7.8)

Далее найдем каждое из слагаемых в скобках под знаком суммы:

()

][][][ aXMXDXM

iii

+σ=+=

][][][

][ a

XMXMXM

XMXXM

jii

−

⎟

⎠

⎞

⎜

⎝

⎛

⎥

⎦

⎤

⎢

⎣

⎡

∑∑

≠

⎟

⎠

⎞

⎜

⎝

⎛

⎥

⎦

⎤

⎢

⎣

⎡

⋅=

∑∑∑∑

≠=== ji

XNXMXM

MXM ][][][

111

][

)1(

−

Подставив найденные выражения в (7.8), получим

+σ

−

−σ=σ

)

откуда видно, что оценка

)

имеет систематическое смещение (–σ

/n). Без ог-

раничения общности будем считать, что

0][

, т.к. мы всегда можем от-

нять

от всех X

. Отметим, что это смещение стремится к нулю при

∞

→n

С целью устранения смещения скорректируем оценку следующим образом:

∑

−

=σ

−

222

)(

)

. (7.9)

Действительно,

222

][

][ σ=σ

−

=σ

)

, т.е. скорректированная по формуле

(7.9) оценка не смещена.

Предложение 7.1. При увеличении объема случайной выборки

)(

σ→−

−

∑

∞→

т.е. оценка (7.9) является состоятельной.

Доказательство. Без ограничения общности считаем, что

0][

. При

этом предположении

. Из (7.9) вытекает, что

][][ σ==

XDXM

⎟

⎠

⎞

⎜

⎝

⎛

−

=σ

∑

Применяя закон больших чисел в форме Хинчина (предложение 5.2) к последо-

вательности

, имеем:

,...,

σ→

→∞

∑

В силу предположения

0][

по закону больших чисел

∞→

→

. Сле-

довательно, 0

∞→

→ . Отсюда вытекает, что . 

σ→

∞→

7.3.3. Сравнение оценок

Предположим, что у нас имеются две несмещенные оценки

),...,('

1 n

XXθ

)

),...,(''

1 n

XXθ

)

для скалярного параметра

∈

. Возникает дилемма, какую из

оценок предпочесть? Простой и разумный совет состоит в том, чтобы выбрать

оценку с

меньшей дисперсией.

Пример 7.1. Предположим, что X

, … , X

– независимая случайная выбор-

ка из равномерного распределения в отрезке

]1,1[

−

, где θ – неизвестный

параметр. Рассмотрим две следующие оценки для

θ:

XXX

=θ ),...,('

)

, 2)max(min),...,(''

1 iin

XXXX +=θ

)

Нетрудно установить, что обе оценки являются несмещенными и

nD 2/1]'[ =θ

)

Немного более сложное вычисление показывает, что )()/1(]''[

∞→Ο=θ nnD

)

Следовательно, при больших n дисперсия второй оценки стремится к нулю

быстрее, чем дисперсия выборочного среднего. Другими словами, при доста-

точно большом объеме выборки оценка

)

становится эффективней оценки '

)

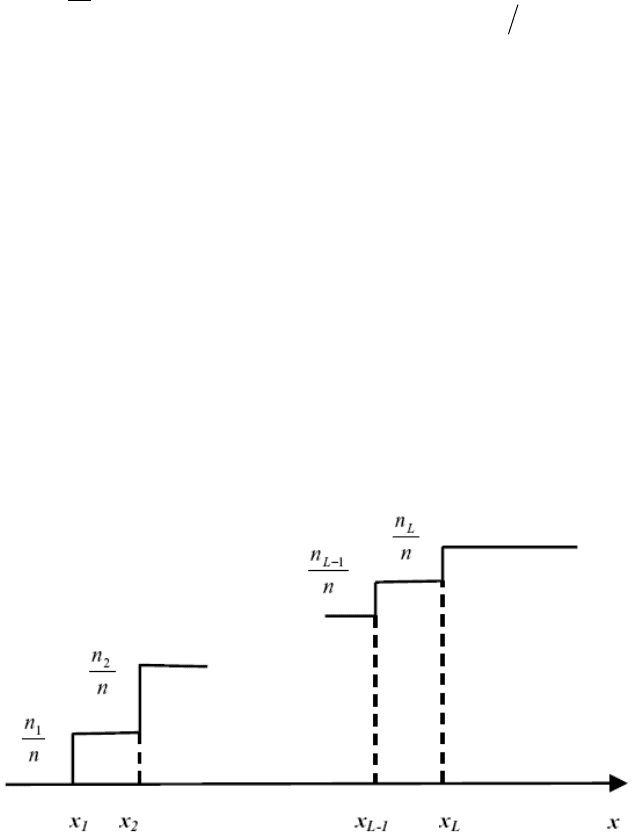
7.4. Оценка функций распределения и плотности

Оценку функции распределения вероятностей F

(x) получаем по тому же

принципу, который был применен при оценивании числовых характеристик:

оценкой функции распределения генеральной случайной величины ξ служит

функция распределения выборки x

, … , x

. На рис. 7.1 приведен пример эмпи-

рической функции распределения.

Рис. 7.1.

Предложение 7.2. Выборочная функция распределения F

(x) в каждой

точке

∞

<<∞−

,, рассматриваемая как функция случайной выборки, схо-

дится по вероятности к теоретической функции распределения в этой точке:

)()( xFxF

n ξ

∞→

→ . (7.10)

Доказательство: Обозначим

}{)( xPxFp

. Тогда случайная выбор-

ка

, … , X

порождает схему Бернулли, на каждом шаге которой может про-

изойти событие {

< x}, i = 1,…, n, или случиться противоположное {X

≥ x},

причем прямое событие на каждом шаге происходит с одинаковыми вероятно-

стями

p = P{X

< x}, поскольку выборочные случайные величины X

распреде-

лены как генеральная случайная величина

ξ.

Тогда значение эмпирической функции распределения в любой точке

x для

конкретной выборки

, … , x

является отношением числа положительных ис-