Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие
Подождите немного. Документ загружается.

Определение 4.2. Распределение случайных величин ξ
1
, … , ξ
n
называется
абсолютно непрерывным, если существует функция
такая, что
),...,(
1...
1
n
xxp
n
ξξ
1)
;
0),...,(,...,
1...1
1
≥∈∀
ξξ nn
xxpRxx
n
2)
;
∫∫
∞
∞−
∞
∞−
ξξ
=1...),...,(...
11...
1
nn
dxdxxxp
n
3)
. (4.1)
∫∫
∞−
ξξ
∞−
ξξ
=∈∀
1
11
),...,(...),...,(...,...,
1...11...1
x
n
x
nnn
xxFdydyyypRxx
n
n
n
Функция
, обладающая перечисленными свойствами, называется
совместной плотностью распределения набора случайных величин
),...,(
1...
1
n
xxp
n
ξξ
n
ξ
ξ ,...,
1
.
Следствие 4.1. В тех точках , в которых плотность
непрерывна, верна формула
n
n
Rxx ∈),...,(
1
),...,(
1...
1
n
xxp
n
ξξ
),...,(
...
),...,(
1...
1
1...
1
1
n
n
n
n
xxp
xx
xxF
n
n
ξξ
ξξ
=
∂∂
∂
. (4.2)
Можно показать, что
.
∫
∞
∞−
ξξ−ξξ
=
−
nnn
dxxxpxxp
nn
),...,(),...,(
1...11...
111
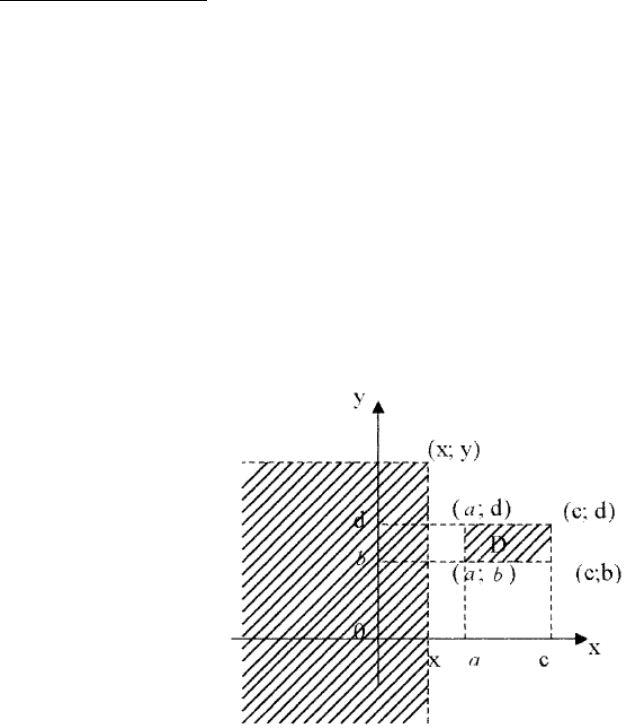
4.1.1. Двумерная случайная величина
Рассмотрим частный случай – двумерную случайную величину (
ξ; η).
Функцией распределения F
ξη
(x, y) случайной величины (ξ ;η) назовем F
ξη
(x, y) =
P(
ξ < x, η < y), т.е. F
ξη
(x, y) − вероятность попадания точки (ξ; η) в левый ниж-
ний бесконечный квадрат плоскости
Оxy с вершиной в точке (x, y).
Рис. 4.1.
Свойства F
ξη
(x, y):
1) 0 ≤ F
ξη
(x, y) ≤ 1;
2)
F
ξη
(x, −∝) = F
ξη
(−∝, y) = F
ξη
(−∝, −∝) = 0;
61
3) F
ξη
(+∝, +∝) = 1;
4) F
ξη
(x, +∝) = F
ξ
(x);
5)
F
ξη
(+∝, y) = F
η
(y);
6) F
ξη
(x, y) − функция неубывающая.
7)
P{(ξ; η) ∈ D} = F
ξη
(c; d) − F(a; d) − F(c; b) + F(a; b).
Случайная величина (
ξ; η) называется дискретной, если ξ и η − дискретные
случайные величины. Простейшей формой закона распределения дискретной
случайной величины является таблица распределения, т.е. перечень возможных
значений (
х
i
; y
i
) и их соответствующих вероятностей p
ij
= P(ξ = х
i
; η = y
j
), где
i = 1; ... ; n; j = 1; ..., m.
Условие нормировки:
. Тогда можно найти:
1
11
=
∑∑
==
n
i
m
j
ji
p
P(ξ = х
i
) =
∑∑
P(η = y
==
==η=ξ
n
j
n
j
jiji
pyxP
11
);(,
j
) = .
∑∑
==
==η=ξ
m
i
m
i
jiji
pyxP
11
);(
η
ξ
y
1
y
2
... y
j
... y
n
x
1
p
11
p
12
... p
1j
... p
1n
x
2
p
21
p
22
... p
2j
... p
2n
... ... ... ... ... ... ...
x
i
p
i1
p
i2
... p
ij
... p
in
... ... ... ... ... ... ...
x
m
p
m1
p
m2
... p
mj
... p
mn
Пример 4.1. Дано распределение двумерной случайной величины
η
ξ
26 30 41 50
2,3 0,05 0,12 0,08 0,04
2,7 0,09 0,30 0,11 0,21
Найти законы распределения составляющих случайных величин ξ и η.
Решение.
ξ
2,3 2,7
Р
0,29 0,71
Действительно,
P(ξ = 2,3) = P(ξ=2,3;η=26) + P(ξ=2,3;η=30) + P(ξ=2,3;η=41) + P(ξ=2,3;η=50) =
= 0,05 + 0,12 + 0,08 + 0,04 = 0,29; аналогично найдем
Р(ξ = 2,7) = 0,71.
η
26 30 41 50
P
0,14 0,42 0,19 0,25
Действительно, Р(η = 26) = Р(ξ=2,3; η=26)+Р(ξ=2,7; η=26) = 0,05+0,09 = 0,14;
62
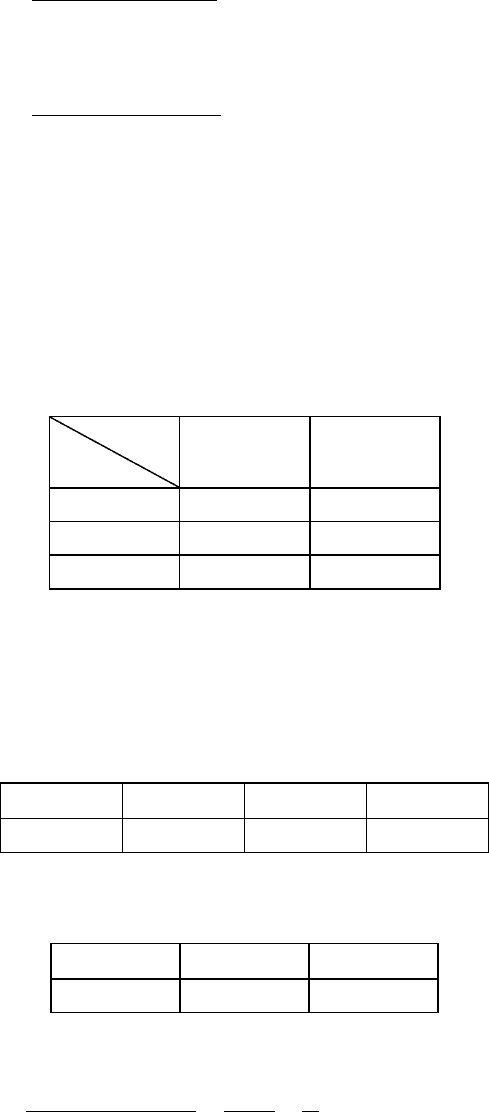
Р(η = 30) = Р(ξ=2,3; η=30)+Р(ξ=2,7;η=30) = 0,12+0,30 = 0,42; аналогично най-
дем Р(η = 41) = 0,19 и Р(η = 50) = 0,25.
4.1.2. Условные законы распределения двумерной дискретной слу-
чайной величины
По теореме умножения вероятностей
P(ξ = х
i
; η = y
j
) = P(ξ = х
i
)⋅P(η = y
j
/ ξ = х
i
) , то
P(η = y
j
/ ξ = х
i
) =
)(
);(
i
ji
xP
yxP
=ξ
=
η
=ξ
.
Аналогично, т.к.
P(ξ = х
i
; η = y
j
) = P(η = y
j
)⋅P(ξ = х
i
/ η = y
j
), то
P(η = y
j
/ ξ = х
i
) =
)(
);(
j
ji
yP
yxP
=η
=
η
=ξ
.
Условным распределением дискретной случайной величины ξ при η = у
j
на-
зовем перечисление возможных значений случайной величины
ξ и их соответ-
ствующих условных вероятностей. Аналогично определяется условное распре-
деление дискретной случайной величины
η при ξ = х
i
.
Пример 4.2. Дано распределение двумерной случайной величины
η
ξ
3 6
10 0,25 0,10
14 0,15 0,05
18 0,32 0,13
Найти: а) законы распределения составляющих ξ и η; б) условный закон
распределения
η при условии, что ξ = 10; в) условный закон распределения ξ
при условии, что
η = 6, и М[ξ / η = 6].
Решение. Закон распределения ξ:
ξ
10 14 18
Р
0,35 0,20 0,45
Закон распределения η:
η
3 6
Р
0,72 0,28
Условный закон распределения η при условии, что ξ = 10. Найдем
P(η = 3 / ξ = 10)=
7
5
35,0
25,0
)10(
)3,10(
==
=ξ
=
η
=ξ
P
P
;
63
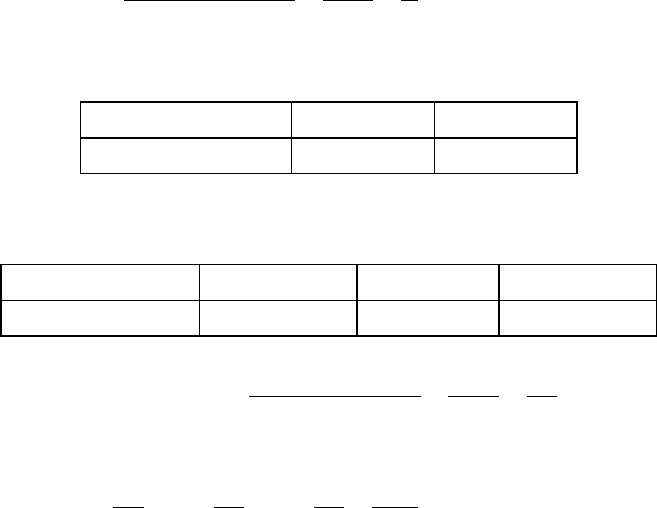
P(η = 6 / ξ = 10) =
7
2
35,0
1,0
)10(
)6,10(
==
=ξ
=
η
=ξ
P
P
Отсюда, условный закон распределения
η при условии, что ξ = 10, имеет вид
η
3 6
P(η / ξ = 10)
5/7 2/7
Условный закон распределения ξ при условии, что η = 6, имеет вид
ξ
10 14 18
P(ξ / η = 6)
10/28 5/28 13/28
Действительно, P(ξ = 10 / η = 6)=
28
10
28,0
10,0
)6(
)6,10(
==
=η
=
η
=
ξ
P
P
.
Аналогично найдем
P(ξ = 14 / η = 6) = 5/28 и P(ξ = 18 / η = 6) = 13/28.
M[ξ / η = 6] = 43,14
28
404
28
13
18
28
5
14
28
10
10
≈=⋅+⋅+⋅ .
4.2. Математическое ожидание функции от случайных величин
Предложение 4.2. Пусть − некоторая функция, зависящая от n
переменных. Тогда
RRg
n
→:
[]
∫∫
∞
∞−
∞
∞−
ξξ
=ξξ
nnnn
dxdxxxpxxggM
n
...),...,(),...,(...),...,(
11...11
1
. #
Математическое ожидание существует тогда и только тогда, когда инте-
грал сходится абсолютно. Из
предложения 4.2 вытекает, в частности, что
[]
∫∫
ξξ
=ξξ
2
21
21212121
),(
R
dxdxxxpxxM
.
Теперь ясно, как вычислять ковариацию:
[]
][][),cov(
212121
ξ
⋅
ξ
−ξξ=ξξ MMM .
Для абсолютно непрерывных случайных величин верны:
- свойство линейности математического ожидания
[]
][...][...
1111 nnnn
McMcccM
ξ
+
+
ξ=
ξ
++ξ
;
- формула для дисперсии суммы
∑
≤<≤
ξ
ξ
+
ξ
+
+ξ
=
ξ++ξ
nji
jinn
DDD
1
11
),cov(2][...][]...[
.
4.3. Независимость случайных величин
Следующее определение обобщает понятие независимости, данное в § 2.9,
на случай произвольных случайных величин.
64
Определение 4.3. Случайные величины ξ
1
, … , ξ
n
называются независимы-
ми
, если
)()...(),...,(,...,
11...1
11
nnn
xFxFxxFxx
nn
ξξξξ
=
∀
.
Следствие 4.2. Случайные величины ξ
1
, … , ξ
n
с абсолютно непрерывным
распределением являются независимыми тогда и только тогда, когда
)()...(),...,(
11...
11
nn
xpxpxxp
nn
ξξξξ
= .
Предложение 4.3. Если ξ
1
и ξ
2
независимы, то для любой пары интервалов
и ] верно равенство
],(
111
baB = ,(
222
baB =
{}{}
{
}
22112211
, BPBPBBP
∈
ξ
⋅
∈ξ=∈ξ∈ξ
. #
Такое же утверждение имеет место для любого конечного числа случайных
величин
, … , :
],(
111
baB = ],(
nnn
baB =
}{}...{},...,{
1111 nnnn
BPBPBBP
∈
ξ
∈
ξ
=∈ξ∈ξ .
Предложение 4.4. Если ξ
1
, … , ξ
n
− независимые абсолютно непрерывные
случайные величины, у которых существует математическое ожидание, то
[]
][]...[...
11 nn
MMM ξξ=ξξ
.
Доказательство. Доказательство просто – последовательно применяем
предложение 4.2, следствие 4.2 и определение 3.8:
[]
==ξξ
∫∫
∞
∞−
∞
∞−
ξξ
nnnn
dxdxxxpxxM
n
...),...,(.........
11...11
1
==
∫∫
∞
∞−
∞
∞−
ξξ
nnn
dxdxxpxpxx
n
...)()...(......
111
1
.
∫∫
∞
∞−
∞
∞−
ξξ
ξξ=⋅⋅= ][]...[)(...)(
1111
1
nnnn
MMdxxpxdxxpx
n
Следствие 4.3. Если ξ
1
, … , ξ
n
− независимы, то
[]
][...][...
11 nn
DDD
ξ
+
+ξ
=
ξ++ξ
.
Доказательство. Достаточно показать, что
0),cov( =ξξ
≠
∀
ji
ji
. Это, в
свою очередь, следует из
предложения 4.4.
4.4. О некоррелированных зависимых случайных величинах
Ниже рассмотрим пример, показывающий, что некоррелированность и не-
зависимость не являются эквивалентными понятиями. Логически этот параграф
продолжает обсуждение, начатое в § 2.10.
Рассмотрим случайную величину
ξ, равномерно распределенную на
, и случайные величины
],[
ππ−
ξ
=
η
cos
1
и
ξ
=
η
sin
2
. Покажем, что
, но случайные величины η
0),cov(
21
=ηη
1
и η
2
зависимы:
65
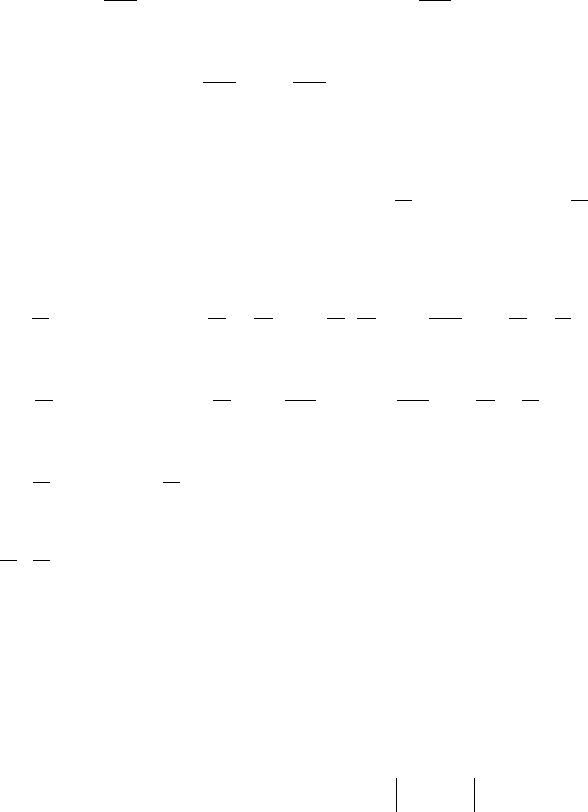
0
2
1
cos][
1
=
π
⋅=η
∫
π
π−
dxxM , 0
2
1
sin][
2
=
π
⋅=η
∫
π
π−
dxxM ,
02sin
4
1
2
1
)sin(cos][
21
=
π
=
π
⋅=ηη
∫∫
π
π−
π
π−
xdxdxxxM .
Тем самым,
и некоррелированность установлена.
0),cov(
21
=ηη
Рассмотрим теперь интервалы
⎥
⎦
⎤
⎢
⎣
⎡
=
2
1
,0
1
B и
⎥
⎦
⎤
⎢
⎣
⎡
=
2
1
,0
2
B , и покажем, что
}{}{},{
22112211
BPBPBBP
∈
η
⋅
∈η
≠
∈η∈η
. Действительно,
6
1
6
2
2
1
2
,
33
,
22
1
,0
1
=
π
⋅⋅
π
=
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
ππ
⎥
⎦
⎤
⎢
⎣
⎡
π
−
π
−∈ξ=
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
∈η
UPP ,
6
1
6
2
2
1
,
6
5
6
,0
2
1
,0
2
=
π
⋅⋅
π
=
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
π
π
⎥
⎦
⎤
⎢
⎣
⎡
π
∈ξ=
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
∈η
UPP ,
0}{
2
1
,0,
2
1
,0
21
=∅=
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
∈η
⎥
⎦
⎤
⎢
⎣
⎡
∈η PP .
Так как
6
1
6
1
0 ⋅≠
, то η
1
и η
2
− зависимые случайные величины.
Замечание 4.2. Мы рассмотрели пример случайных величин, которые, оче-
видным образом, являются
функционально зависимыми: ,
2
2
2
1
))((1))(( ωη−=ωη
но их коэффициент корреляции равен нулю:
0),(
21
=
η
η
ρ
. Это резко контрасти-
рует со случаем линейной зависимости между случайными величинами, кото-
рая имеет место тогда и только тогда, когда
1),(
=
η
ξ
ρ
(см. § 2.10). Таким обра-
зом, можно сказать, что коэффициент корреляции отражает
степень линейной
зависимости
между случайными величинами.
4.5. Преобразования случайных величин
4.5.1. Преобразования одной случайной величины
Пусть непрерывная случайная величина ξ имеет функцию F
ξ
(x) и плот-
ность
p
ξ
(x) распределения. Построим с помощью функции
R
R
g
→:
случайную
величину
η = g(ξ). Требуется найти функцию распределения и, если существу-
ет, плотность распределения
η.
Замечание 4.3. Плотность распределения случайной величины η = g(ξ)
существует далеко не при любых функциях
g. Так, если функция g кусочно-
постоянна, то случайная величина
η имеет дискретное распределение, и плот-
ность ее распределения не существует. Плотность распределения
p
η
(x) заведомо
существует, если, например, функция
g монотонна («строго монотонна»).
66
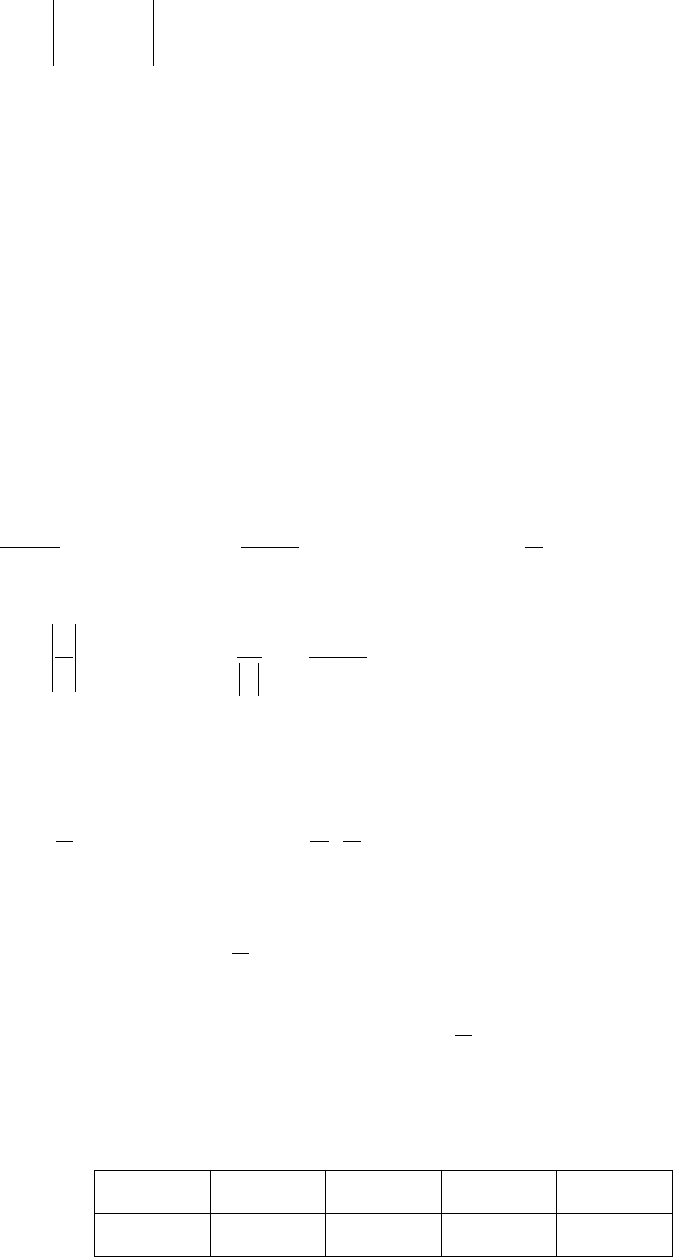
Предложение 4.5. Пусть ξ имеет функцию F
ξ
(x) и плотность p
ξ
(x) распре-
деления, и функция
R
R
g
→:
монотонна. Тогда случайная величина η = g(ξ)
имеет плотность распределения
()(
)()()(
11
xgpxgxp
−
ξ
−
η
⋅
′
=
)
, (4.3)
где )
− функция, обратная к g. #
(
1
⋅
−
g
Можно показать, что для нахождения числовых характеристик случайной
величины
η = g(ξ) достаточно лишь знание закона распределения аргумента:
∫
∞
∞−
ξ
=ξ=η dxxpxggMM )()()]([][ , (4.4)
()
∫
∞
∞−
ξ
η−=ξ=η dxxpMxggDD )(][)()]([][
2
. (4.5)
Пример 4.3. Найти плотность вероятности случайной величины ba
+
ξ
=
η ,
где 0
, ξ имеет функцию F≠a
ξ
(x) и плотность p
ξ
(x) распределения.
Решение. Согласно предложению 4.5 имеем:
a
bx
xg
a
b
−
=⇒
−η
=ξ
−
)(
1
, тогда
(
)
a
xg
1
)(
1
=
′
−
, отсюда по формуле (4.3)
плотность вероятности случайной величины
ba
+
ξ
=
η
равна
(
)
⎟
⎠
⎞
⎜
⎝
⎛
−
=⋅=
ξ
−
ξη
a
bx
p
a
xgp
a
xp
1
)(
1
)(
1
.
Пример 4.4. Найти математическое ожидание и дисперсию случайной ве-
личины
, если плотность распределения случайной величины ξ
есть
ξ−=η sin32
xxp cos
2
1
)( =
ξ
на отрезке
⎥
⎦
⎤
⎢
⎣
⎡
ππ
−
2
,
2
.
Решение. Используем формулы (4.4), (4.5):
2cos
2
1
)sin32(][
2/
2/
=⋅−=η
∫
π
π−
xdxxM ,
()
3472cos
2
1
)sin32(][][][
2
2/
2/
2
2
2
=−=−⋅−=η−η=η
∫
π
π−
xdxxMMD .
Рассмотрим дискретную случайную величину
ξ с рядом распределения
ξ
x
1
x
2
…
x
n
P
p
1
p
2
…
p
n
Если различным возможным значениям случайной величины ξ соответст-
вуют различные значения случайной величины
η, то вероятности соответст-
67
вующих значений случайных величин ξ и η равны, т.е. если Р(ξ = х
i
) = p
i
, то и
P(η = ϕ(x
i
)) = p
i
.
Пример 4.5. Пусть имеем дискретную случайную величину ξ
ξ
−2
3 5
Р
0,3 0,6 0,1
и η = ξ
2
, то
η
4 9 25
P
0,3 0,6 0,1
Если различным возможным значениям случайной величины ξ соответст-
вуют значения
η, среди которых есть равные между собой, то вероятности по-
вторяющихся значений случайной величины
η равны суммам вероятностей со-
ответствующих значений случайной величины
ξ.
Пример 4.6. Найти ряд распределения случайной величины η = ξ
2
, если
ξ
−2
1 2 3
Р
0,1 0,3 0,2 0,4
Решение. Поскольку P(η = 4) = P(ξ = −2) + P(ξ = 2) = 0,1 + 0,2 = 0,3;
P(η = 1) = P(ξ = 1) = 0,3; P(η = 9) = P(ξ = 3) = 0,4; то
η
1 4 9
P
0,3 0,3 0,4
4.5.2. Композиция законов распределений
Многие важные случайные величины представляются в виде сумм незави-
симых слагаемых. Нижеследующее утверждение устанавливает, как распреде-
ление суммы связано с распределениями слагаемых. Вид закона распределения
суммы случайных величин не совпадает с законами распределения слагаемых.
Определение 4.4. Композицией законов распределений называется преобра-
зование, по которому можно получить закон распределения суммы случайных
величин на основе совместного закона распределения случайных величин.
Предложение 4.6. Пусть случайные величины ξ
1
и ξ
2
независимы и абсо-
лютно непрерывны с плотностями
и ). Тогда
)(
1
xp
ξ
(
2
xp
ξ
∫
∞
∞−
ξξξ+ξ
−= dyyxpypxp )()()(
2121
. # (4.6)
68
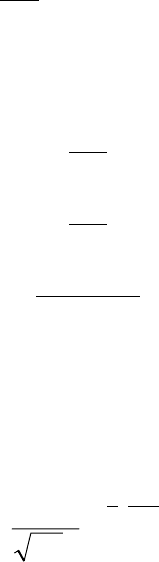
Замечание 4.4. Если f и g − абсолютно интегрируемые функции на R, то
определена
операция свертки функций f и g:
∫
∞
∞−
−=∗ dyyxgyfxgf )()())((
&
.
69
)
Таким образом,
предложение 4.6 гласит, что если ξ
1
и ξ
2
независимые случай-
ные величины, имеющие плотность, то )(()(
2121
xppxp
ξξξ+ξ
∗
=
.
Предложение 4.7. Сумма произвольного числа независимых нормальных
случайных величин имеет нормальное распределение.
#
Рассмотрим часто используемые, функции от случайных величин.
Пример 4.7. (Композиция равномерных распределений). Даны независимые
равномерно распределенные случайные величины
ξ
1
и ξ
2
с параметрами l
1
и l
2
.
Требуется найти: а) совместный закон распределения случайных величин
ξ
1
и
ξ
2
; б) закон распределения случайной величины ξ = ξ
1
+ ξ
2
.
Решение. Так как случайные величины ξ
1
и ξ
2
− независимые, то, учитывая
следствие 4.3, совместная плотность распределения имеет вид:
],,0[,],0[
2211
lxlx
∈
∈
⎪
⎩
⎪
⎨
⎧
==
ξξξξ
,0
,
1
)()(),(
21
2121,
2121
ll
xpxpxxp
в противном случае.
Пусть для определенности
l
1
≤ l
2
. Тогда, согласно (4.6), плотность суммы
∫
∞
∞−
ξξξ+ξ
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+≤<
−+
≤<
≤<
=−=
.,
,,
,0,
)()()(
212
21
21
21
21
1
1
21
2121
llxl
ll
xll
lxl
ll
l
lx
ll
x
dyyxpypxp
Пример 4.8. (Композиция нормальных законов распределений). Применив
аналогичные как в
примере 4.5 рассуждения, получим, что плотность распреде-
ления суммы случайных величин
и равна
),(~
2
111
σξ aN ),(~
2
222
σξ aN
),(
2
1
)()()(
2
2
1
2
2121
σ=
σπ
=−=
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
−
∞
∞−
ξξξ+ξ
∫
aNedyyxpypxp
ax
,
где
, т.е. композиция нормальных законов
распределения снова приводит к нормальному закону распределения.
21
2
2
2
1
2
21
21
2, σσρ+σ+σ=σ+=
ξξ
aaa
Пример 4.9. (Распределение χ
2
−Пирсона). Распределением χ
2
−Пирсона с n
степенями свободы называется распределение суммы квадратов
n независимых
стандартных нормальных случайных величин:
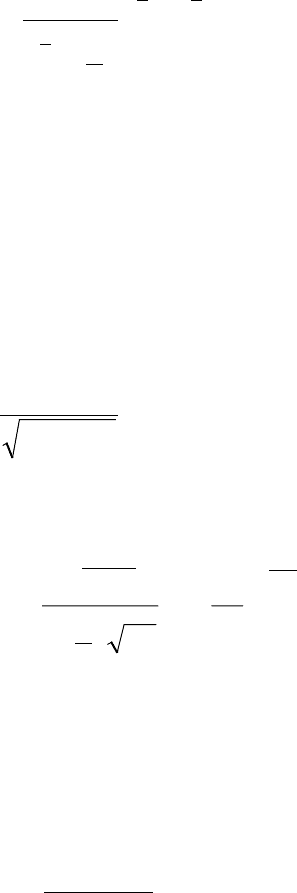
)1,0(~,)(
1
22
Nn
i
n
i
i
ξξ=χ
∑
=
.
Плотности распределения случайных величин
χ
2
(n) имеют вид:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<
≥
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
−−
,0,0
,0,
2
2
1
)(
2
1
2
2
x
xex
n
xf
xn
n
где
− гамма-функция.
∫
∞
−−
=Γ
0
1
)( dzzep
pz
Пример 4.10. (Распределение Стьюдента). Распределение Стьюдента бы-
ло введено в 1908 г. английским статистиком В. Госсетом, публиковавшемся
под псевдонимом «Стьюдент». Закону распределения Стьюдента с
n степенями
свободы удовлетворяет отношение
nn
nt
/)(
)(
2
χ
ξ
=
,
где
ξ − стандартная нормальная случайная величина, независимая от χ
2
.
Плотность распределения Стьюдента равна
2
1
2
)(
1
2
2
1
)(
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
n
nt
n
x
n
n
n
xp .
При плотность распределения Стьюдента сходится к плотности стан-
дартной нормальной случайной величины.
∞→n
Пример 4.11. (Распределение Фишера). F−распределением Фишера с
степенями свободы называется распределение случайной величины, равное
),( nm
nn
mm
nmF
/)(
/)(
),(
2
2
χ
χ
= .
4.6. Многомерное нормальное распределение
Важнейшим примером совместного распределения нескольких случайных
величин является многомерное нормальное распределение. Оно играет важную
роль в теории вероятностей и часто возникает в различных приложениях.
Определение 4.5. Говорят, что набор случайных величин
),...,(
1 n
ξ
ξ
=ξ
имеет многомерное нормальное (или гауссовское) распределение, если найдутся
вещественный вектор )
, невырожденная вещественная n × n − мат-
,...,(
1 n
aa=a
70
