Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие

Подождите немного. Документ загружается.

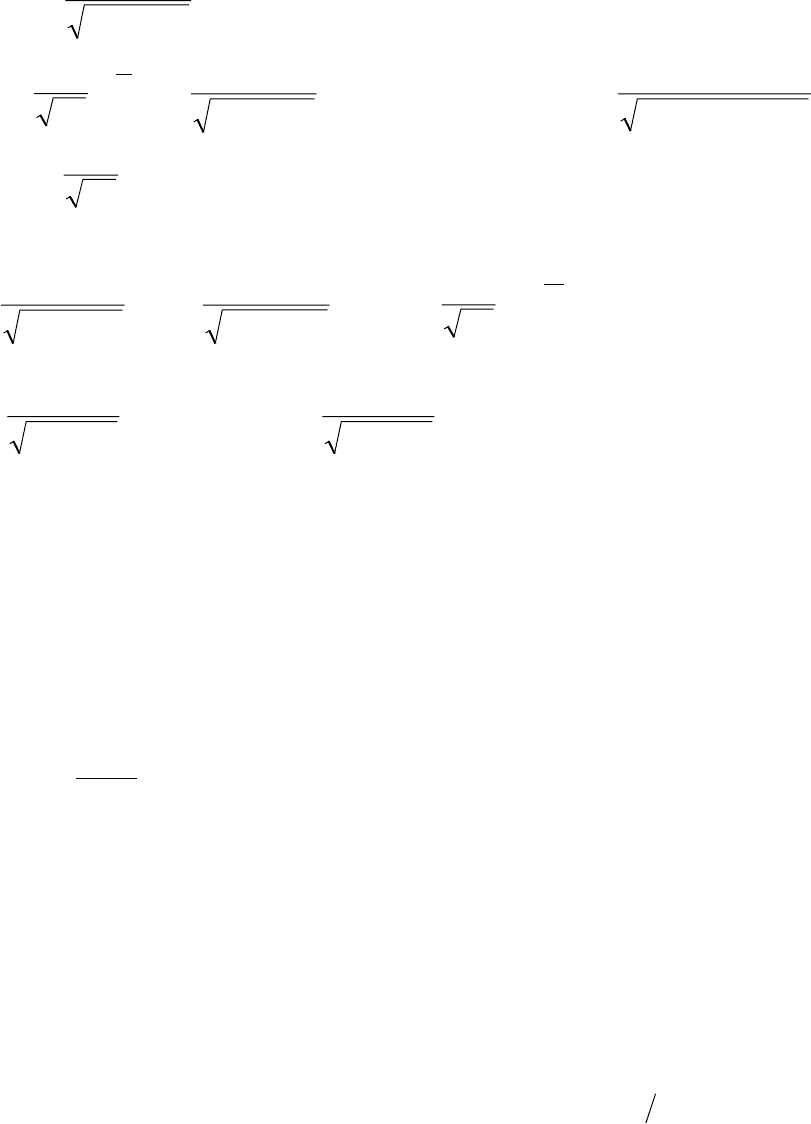
Решение. Поскольку количество грибов n – велико, то используем вместо

биномиального распределения его аппроксимацию. В данном случае p = 0,25.

При этом: , 107525,0300 >=⋅=np 2025,5675,025,0300)1( >=

⋅

−

np , по-

этому используем нормальную аппроксимацию.

а) Если вероятность p наступления события A в каждом испытании посто-

янна и отлична от 0 и 1, то вероятность

того, что событие A произойдет

k раз в достаточно большом числе n независимых испытаниях приближенно

вычисляется по формуле (2.12):

)(

)1(

)(

pnp

−

≈

где

)(

etf

−

)1( pnp

npk

−

Отсюда получим:

75,025,0300

25,030075

⋅⋅

⋅−

39894,0

)0()(

== eftf

0532,0)75(

25,0;300

б) Применяем формулу (2.13):

(

)

)()(

1020,

tFtFdvcP

npn

−→

≤

где

;

)1(

pnp

npc

−

;

)1(

pnp

npd

−

∫

∞−

−

dxetF

)( − кривая Гаусса, зна-

чения которой определяются из таблиц. Имеем:

33333,3

75,075

7550

−=

⋅

−

33333,3

75,075

75100

⋅

−

99914,000043,099957,0)33333,3()33333,3()()(

001020

−

− FFtFtF

Таким образом,

()

99914,010050

25,0;300

≈

≤

≤ kP

2.12. Неравенства Чебышева

Предложение 2.16. (Первое неравенство Чебышева). Если случайная ве-

личина ξ принимает только неотрицательные значения и имеет математическое

ожидание, то для любого положительного числа ε:

()

≤ε≥ξ

][M

. (2.14)

Доказательство. Замечая, что

{} {}

1)()(

ε<ξε≥ξ

, и, пользуясь основ-

ными свойствами математического ожидания (предложение 2.5), получим

{} {} {}

{

}

≥

≥ξ+ξ=ξ

ε≥ξε<ξε≥ξ

PIMIMIMM ][][][][

. 

Пример 2.21. Сумма всех вкладов в банке составляет 2 млн. руб., а вероят-

ность того, что случайно взятый вклад не превысит 10 тысяч руб., равна 0,6.

Что можно сказать о числе вкладчиков?

Решение. Пусть ξ − размер случайно взятого вклада, а n − число всех

вкладчиков. Тогда средний размер вклада равен:

nM 2000][

(тыс. руб.). Со-

гласно неравенству (2.14):

()

][

≤≤ξ

или

()

2000

110 −≥≤ξ

. Учитывая,

что

, получим

()

6,010 =≤ξP

6,0

200

1 ≤−

, откуда 500

≤

n .

Предложение 2.17. (Второе неравенство Чебышева). Для любой случай-

ной величины, имеющей математическое ожидание и дисперсию, и произволь-

ного ε > 0 справедливо неравенство:

{}

][

≤ε>ξ−ξ

. (2.15)

Доказательство. Применим первое неравенство Чебышева (2.14) к слу-

чайной величине

, взяв в качестве положительного числа ε

])[( ξ−ξ=ξ

′

][]])[[(

}])[({

ξ−ξ

≤ε>ξ−ξ

DMM

. (2.16)

Очевидно, что

}])[({}][{

ε>ξ−ξ=ε>ξ−ξ MPMP

. Тогда из (2.16) следует до-

казываемое неравенство. 

Учитывая, что события

−

][M

≤

−

][M

противоположны, не-

равенство Чебышева можно записать в другой форме:

][

1}][{

−≥ε≤ξ−ξ

. (2.17)

Пример 2.22. Случайная величина ξ имеет дисперсию 0,004. Найти вероят-

ность того, что случайная величина ξ отличается от М[ξ] более чем на 0,2.

Решение. В соответствии с неравенством (2.17) получаем

1,0

04,0

004,0

)2,0(

004,0

}2,0][{

==≤>ξ− MXP

Замечание 2.15. Неравенство Чебышева применимо для любых случайных

величин. В форме (2.15) оно устанавливает верхнюю границу, а в форме (2.17) −

нижнюю границу вероятности рассматриваемого события.

2.13. Теорема Чебышева

Предложение 2.18. (Теорема Чебышева). Пусть

...,,...,

1 n

– независимы и

. Тогда

CDi

≤ξ∀ ][

0>ε∀ при

][...][...

→

⎭

⎬

⎫

⎩

⎨

⎧

ε>

ξ++ξ

−

ξ++ξ

∞→

. (2.18)

Доказательство. Обозначим n

/)(

K . Тогда левая часть (2.18)

запишется в виде

{

}

>η−η ][MP . Применяя второе неравенство Чебышева и

замечание 2.13, получим, что эта вероятность может быть оценена сверху сле-

дующим образом:

⎥

⎦

⎤

⎢

⎣

⎡

ξ++

≤

⎭

⎬

⎫

⎩

⎨

⎧

ε>

ξ++ξ

−

ξ++ξ

...

][

][...][...

[]

22222

][...][...

≤

ξ++ξ

Последнее выражение, очевидно, стремится к нулю при . 

∞→n

Если все случайные величины ξ

, …, ξ

, … имеют одно и то же распреде-

ление, теорема Чебышева обретает следующую форму.

Следствие 2.1. Пусть ξ

, … , ξ

, … – независимые одинаково распределен-

ные случайные величины с конечной дисперсией:

∞

][

. Пусть aM

][.

Тогда 0 при >ε∀

...

→

⎭

⎬

⎫

⎩

⎨

⎧

ε>−

ξ++ξ

∞→ a

Выведем отсюда закон больших чисел для последовательности независи-

мых испытаний. Для этого вспомним, что число успехов

может быть пред-

ставлено в виде суммы независимых одинаково распределенных случайных ве-

личин с бернуллиевским распределением (см. пример 2.13). Непосредственно

получаем следующее утверждение, которое известно как теорема Бернулли.

Следствие 2.2. (Теорема Бернулли). Пусть

– число успехов в последова-

тельности из n независимых испытаний Бернулли с вероятностью успеха в еди-

ничном испытании p. Тогда

⎭

⎬

⎫

⎩

⎨

⎧

ε>−

, или 0>

∀

при 0→

⎭

⎬

⎫

⎩

⎨

⎧

ε>−

∞→ p

. 

Пример 2.23. При штамповке пластинок из пластмассы брак составляет

3%. Найти вероятность того, что при проверке партии в 1000 пластинок вы-

явится отклонение от установленного процента брака меньше чем на 1%.

Решение. Из условия задачи следуют, что n = 1000, p = 0,03,

q = 1 − p = 0,97, ε = 0,01. Запишем теорему Бернулли через вероятность проти-

воположного события, а именно

709,0

1,0

0291,0

01,01000

97,003,0

=−=

⋅

−=

−≥

⎭

⎬

⎫

⎩

⎨

⎧

ε<−

Таким образом, искомая вероятность Р ≥ 0,709.

Замечание 2.16. Теорема Бернулли имеет важное методологическое значе-

ние, связанное с возможностью «частотного определения». Допустим, нас ин-

тересует вероятность некоторого случайного события A, которое может про-

изойти в результате проведения некоторого опыта. Предположим, что имеется

принципиальная возможность воспроизводить неограниченное количество раз

условия опыта. Пусть

− число появлений события A при n независимых по-

вторениях опыта. Тогда по теореме Бернулли имеет место устойчивость час-

тот, а именно при больших n значения v

/n будут колебаться около некоторого

числа, которое и есть вероятность P(A).

Однако следует учесть, что свойство устойчивости частот (равная веро-

ятность успеха в единичном испытании) не всегда может иметь место на

практике. Наличие теоремы ничего не может диктовать природе – в природе

может иметь место устойчивость частот, а может и

не иметь. Такие величины

называют неопределенными. Этот вопрос тесно примыкает к проблеме различ-

ных подходов к определению понятия вероятности и к проблеме границ приме-

нимости теории вероятностей.

Утверждения этого параграфа становятся более краткими, если ввести ни-

жеследующее понятие.

Определение 2.13. Последовательность случайных величин сходит-

ся по вероятности к случайной величине ξ, если

{}

∞

0>ε∀ при

{

}

0→

−

ξ∞→

Кратко это записывают следующим образом:

. ξ→ξ

Таким образом, утверждения следствий 2.1 и 2.2 кратко записываются, как

→

ξ++ξ

→

, соответственно.

Предложение 2.19. Пусть , и числовая последовательность

при . Тогда и . #

ξ→ξ

η→η

→ ∞→n

ξ→ξ cc

η+ξ→η+ξ

Глава 3. Общие случайные величины

Дискретные вероятностные пространства, рассмотренные в предыдущей

главе, обладают ограничением: определенные на них случайные величины мо-

гут принимать не более чем счетное число значений. Как с точки зрения разви-

тия теории, так и из потребностей практических приложений, часто необходи-

мо рассматривать случайные величины с непрерывными значениями. Теория,

позволившая строго изучать общие

случайные величины была построена в 1933

году выдающимся отечественным математиком А.Н. Колмогоровым. Предло-

женный им подход получил название

аксиоматики теории вероятностей Кол-

могорова

. Он привлекает математический аппарат теории меры для задания ве-

роятностей, и интегрирование по Лебегу для вычисления математических ожи-

даний. Эти вопросы лежат вне рамок данного курса, поэтому в следующем па-

раграфе мы с целью общего ознакомления лишь коснемся вопросов, связанных

с определением общего вероятностного пространства по Колмогорову.

3.1. Общее определение вероятностного пространства

В отличие от рассматривавшейся нами ранее дискретной ситуации, где ве-

роятностным пространством была названа пара (

Ω, P), под общим вероятност-

ным пространством следует понимать тройку объектов (

Ω, F, P), смысл кото-

рых раскрывается следующими определениями.

Определение 3.1. Вероятностным пространством называется тройка

(

Ω, F, P), где Ω – произвольное множество (элементарных исходов), F – σ−ал-

гебра подмножеств множества

Ω (события), P – вероятностная мера на (Ω, F).

Определение 3.2. Система F подмножеств множества Ω называется σ−ал-

геброй

, если:

Ω ∈ F (Ω – единица в σ−алгебре), ∅ ∈ F;

2) Если

FAA

∈

,...,...

, то и , т.е. F замкнуто относительно

счетных объединений и пересечений;

∈

∞

∈

∞

3) Если

∈,, то

∈

Определение 3.3. Вероятностной мерой P называется отображение

→:

, обладающее следующими свойствами:

0)( ≥∈∀

1)( =Ω

3) Если

FAA

∈

,...,...

∅

≠∀

AAji I , то .

∑∑

∞

⎟

⎠

⎞

⎜

⎝

⎛

)(

APAP

В рамках такого подхода элементы

F трактуются как события.

Замечание 3.1. Дискретное вероятностное пространство вкладывается в

эту схему. В качестве

σ−алгебры событий F здесь выступает множество все-

возможных подмножеств дискретного множества

Ω.

3.2. Случайные величины (общий случай)

Определение 3.4. Случайной величиной ξ = ξ(ω) называется такое отобра-

жение

, что

R→Ωξ: F

∈

≤

∈∀ })(:{

Можно показать, что если

)(

– случайная величина, то

Rba

∈

∀ ,,

}{

>ξ

}{

<ξ

, ,

}{ ba ≤ξ<

}{ ba

≤

(3.1)

есть события. Идея такого определения случайной величины состоит в том,

чтобы обеспечить тот факт, что множества вида (3.1) являются событиями.

В общем случае распределение случайных величин описывается в терми-

нах функций распределений.

Определение 3.5. Функцией распределения случайной величины ξ называ-

ется функция

, определяемая следующим образом RRF →

}{)( xPxF <ξ=

Приращения функции распределения имеют очень простой смысл:

}{}{}{)()( baPaPbPaFbF

≤

−<ξ

−

ξξ

. (3.2)

Предложение 3.1. Имеют место следующие общие свойства функций рас-

пределения

1)(0 ≤≤∀

xFx

(x) – неубывающая функция:

)()(

2121

xFxFxx

ξξ

≤

∀

3) Пределы на бесконечности:

0)(lim)(

−

∞

−∞→

xFF

, 1)(lim)(

=+∞

+∞→

xFF

4) Функция

(x) непрерывна слева в каждой точке:

)()(lim)0(

xFyFxF

ξξ

−→

==−

. #

Пример 3.1. Простейший случай – константа: ξ(ω) = c. В этом случае

Пример 3.2. Дискретная случайная величина ξ – число выпавших очков на

игральной кости:

Замечание 3.2. Каков вероятностный смысл точки разрыва функции рас-

пределения? Ответ на этот вопрос получится, если в (3.2) положить

, а a

устремить к x слева:

)0()(}{

−

=ξ

ξξ

xFxFxP

. Чтобы строго обосновать этот

вывод, следует воспользоваться свойствами вероятностной меры из § 3.1. Та-

ким образом, функция распределения имеет разрыв в точке x тогда и только то-

гда, когда

0}{ >=ξ

. Более того, величина скачка в точке разрыва совпадает с

этой вероятностью.

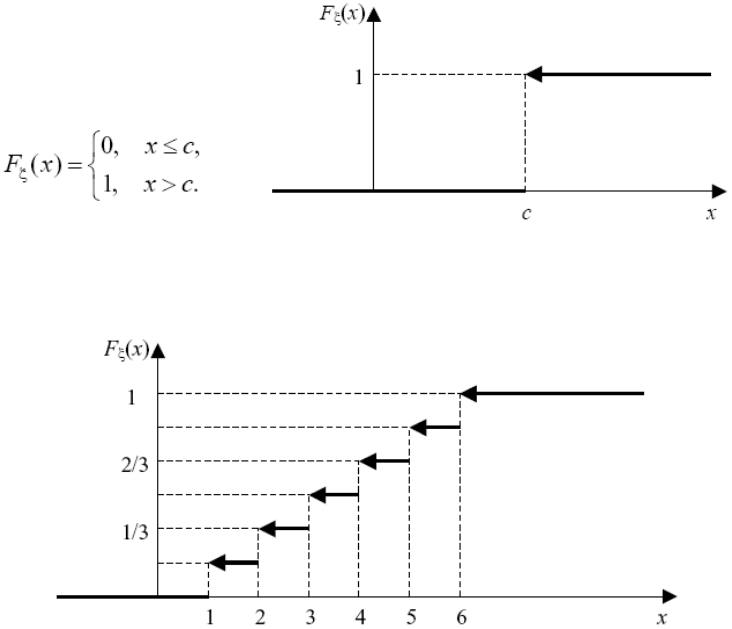
Пример 3.3. Среди шести элементов два изношенных. Составить ряд рас-

пределения случайной величины Х – числа изношенных элементов среди трех

наудачу отобранных. Найти функцию распределения F(x) и построить ее гра-

фик.

Решение. Случайная величина Х может принимать значения: 0; 1; 2.

P(Х = 0) =

⋅

2,0

!6!1!3!2!0

!3!3!4!2

⋅

⋅⋅

⋅

; Р(Х = 1) =

6,0

⋅

;

Р(Х = 2)=

.2,0

⋅

Условие нормировки: 0,2 + 0,6 + 0,2 = 1.

0 1 2

0,2 0,6 0,2

Найдем F(x):

если x ∈ (-∞; 0], то F(x) = P(X < x) = 0;

если x ∈ (0; 1], то F(x) = P(X < x) = P(X = 0) = 0,2;

если x ∈ (1; 2], то F(x) = P(X < x) = P(X = 0) + P(X = 1) = 0,2 + 0,6 = 0,8;

если x ∈ (2; +

), то F(x) = P(X < x) = P(X = 0) + P(X = 1) + P(X = 2) =

∞

= 0,2 + 0,6 + 0,2 = 1.

Следовательно,

⎪

⎩

⎪

⎨

⎧

∞+∈

∈

−

∞

∈

).;2(,1

],2;1(,8,0

],1;0(,2,0

],0;(,0

)(

Итак,

∑

)(

pxF

, т.е. суммируем те p

, для которых x

< x.

Зная F(x), можно, например, найти Р(Х

= 3) = 0, т.к. x = 3 – точка непрерыв-

ности F(x); или найти Р(Х

= 1) = 0,8 – 0,2 = 0,6, т.к. x = 1 – точка разрыва F(x);

или P(–1

≤ X < 1,5) = F(1,5) – F(–1) = 0,8 – 0 = 0,8.

3.3. Непрерывные случайные величины

3.3.1. Понятие непрерывной случайной величины

Случайная величина, значения которой заполняют некоторый промежуток,

называется непрерывной. В частности, это может быть не один промежуток, а

объединение нескольких. Промежутки могут быть конечными, полубесконеч-

ными или бесконечными, например:

];( ba );( b

−

∞

);[

∞

, .

);( ∞−∞

Вообще непрерывная случайная величина – это абстракция. Снаряд, выпу-

щенный из пушки, может пролететь любое расстояние, скажем, от 5 до 5,3 км.,

но никому не придёт в голову измерять эту величину с точностью до 0,000001

км. (т.е. до миллиметра), не говоря уже об абсолютной точности. На практике

такое расстояние будет дискретной случайной величиной,

у которой одно зна-

чение от другого отличается по крайней мере на 1 метр. При описании непре-

рывной случайной величины принципиально невозможно выписать и зануме-

ровать все ее значения, принадлежащие даже достаточно узкому интервалу.

Эти значения образуют несчетное множество, называемое «континуум».

Если ξ − непрерывная случайная величина, то равенство ξ = x представляет

собой, как и в случае дискретной случайной величины, некоторое случайное

событие, но для непрерывной случайной величины это событие можно связать

лишь с вероятностью, равной нулю, что однако не влечёт за собой невозможно-

сти события. Так, например, можно говорить, что только с вероятностью

«нуль» снаряд пролетит 5285,6287 метра, или что отклонение действительного

размера детали от номинального составит 0,001048 миллиметра. В этих случаях

практически невозможно установить, произошло событие или нет, так как из-

мерения величин проводятся с ограниченной точностью, и в качестве результа-

та измерения можно фактически указать лишь границы более или менее узкого

интервала, внутри которого находится измеренное значение.

Значениям непрерывной случайной величины

присуща некоторая неопре-

деленность. Например, нет практического смысла различать два отклонения от

номинального размера, равные 0,4 мм и 0,4000025 мм. Вероятность, отличная

от нуля, может быть связана только с попаданием величины в заданный, хотя

бы и весьма узкий, интервал. Здесь можно привести сравнение с распределени-

ем массы вдоль стержня.

Определение 3.6. Случайную величину назовем непрерывной, если ее

функция распределения F

(x) непрерывна.

Легко видеть (см. замечание 3.2), что случайная величина непрерывна то-

гда и только тогда, когда

{}

ξ xP при всех x.

Важный класс непрерывных случайных величин – абсолютно непрерыв-

ные случайные величины. Это случайные величины, распределение которых

имеет плотность распределения.

Определение 3.7. Случайная величина ξ называется абсолютно непрерыв-

ной, если существует функция p

(x) такая, что

1) p

(x) ≥ 0,

– условие нормировки непрерывной случайной величины ξ,

∫

∞

∞−

=1)( dxxp

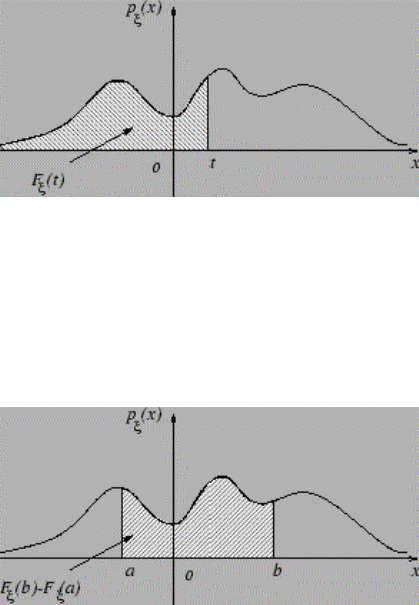
∈∀ имеет место равенство (см. рис. 3.1): .

∫

∞−

ξξ

tFdxxp )()(

Функция p

(x), обладающая вышеперечисленными свойствами, называется

плотностью распределения случайной величины ξ.

Следствие 3.1. Если ξ – абсолютно непрерывная случайная величина, то

}{)()()( baPaFbFdxxp

<ξ≤=−=

ξξξ

∫

Рис. 3.1.

Т.к. вероятность попадания непрерывной случайной величины ξ в точку

равна нулю, имеем P(a ≤ ξ < b) = P(a ≤ ξ ≤ b) = Р(a <ξ ≤ b) = Р(a < ξ < b).

Наглядный смысл плотности можно проиллюстрировать рис. 3.2.

Рис. 3.2.

Замечание 3.3. Если плотность p

(x) непрерывна в точке x, то из cледст-

вия 3.1 следует, что при

0→∆

)()()()(}{ xoxxpxFxxFxxxP

∆

−

∆

+≤ξ≤

ξξξ

Следствие 3.2. Если x – точка непрерывности функции p

(x), то

)()( xpxF

ξξ

′

3.3.2. Примеры абсолютно непрерывных распределений

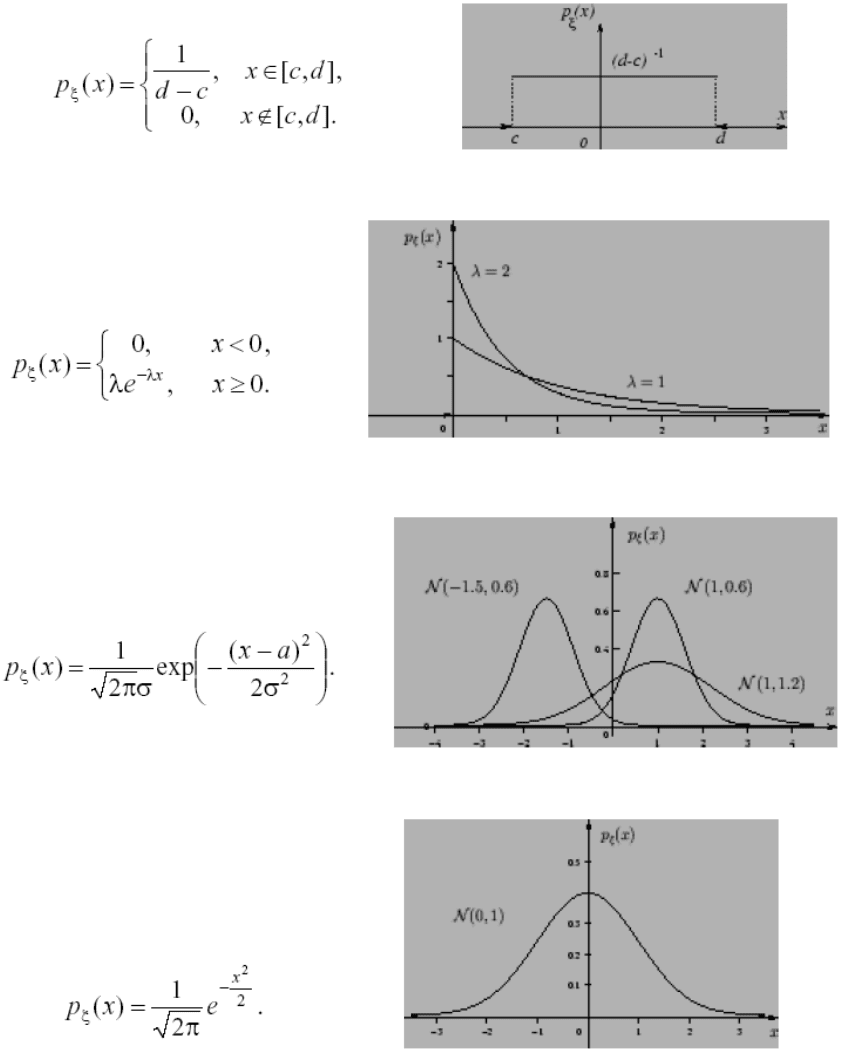
1) Равномерное распределение на отрезке : ],[ dc

2) Показательное (или экспоненциальное) распределение с параметром λ > 0:

3) Нормальное (или гауссовское) распределение ), ,(

σaN

a ∈ , : 0>σ

Стандартное нормальное распределение − N(0, 1):

Пример 3.4. Случайная величина ξ задана функцией распределения