Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие
Подождите немного. Документ загружается.

809,0458,0351,0)()()()(
=
+
=
+=+=
B
P
A
P
B
A
P
C
P
.
Пример 1.12. Для получения кредита предприятие обратилось к трем бан-
кам. Статистические исследования показали, что вероятности выделения кре-
дита этими банками соответственно равны р
1
= 0,5, р
2
= 0,4 и р
3
= 0,9. Банки
выделяют кредит независимо друг от друга и, если примут решение о его выде-
лении, то в размере: первый банк – 160 млн. руб., второй – 40 млн. руб., третий
– 200 млн. руб. Найти вероятности того, что предприятие получит кредит в
размере: а) 200 млн. руб.; б) не менее 240 млн. руб.; в) любом.
Решение. Введем события
: А – первый банк выделит кредит; В – второй
банк выделит кредит; С – третий банк выделит кредит; D – предприятие полу-
чит кредит в размере 200 млн. руб.; E – предприятие получит кредит в размере
не менее 240 млн. руб.; F – предприятие получит кредит.
а) Т.к. D = A⋅B, то
P(D) = 0,5⋅0,4⋅(1 – 0,9) + (1 – 0,5)⋅(1 – 0,4)
⋅0,9 = 0,02 + 0,27 = 0,29.
б) Т.к. E =
C
B
A
C
B
A
C
B
A
⋅
⋅
+
⋅
⋅+⋅
⋅
, то
P(E) = 0,5⋅(1 – 0,4)⋅0,9 + (1 – 0,5)⋅0,4⋅0,9 + 0,5⋅0,4⋅0,9 = 0,63.
в) Т.к.
C
B
A
F ⋅
⋅
= , то P(F) = 1 – P( C
B
A
⋅
⋅
) = 1 – 0,5⋅0,6⋅0,1 = 0,97.
1.9. Формула полной вероятности и формула Байеса
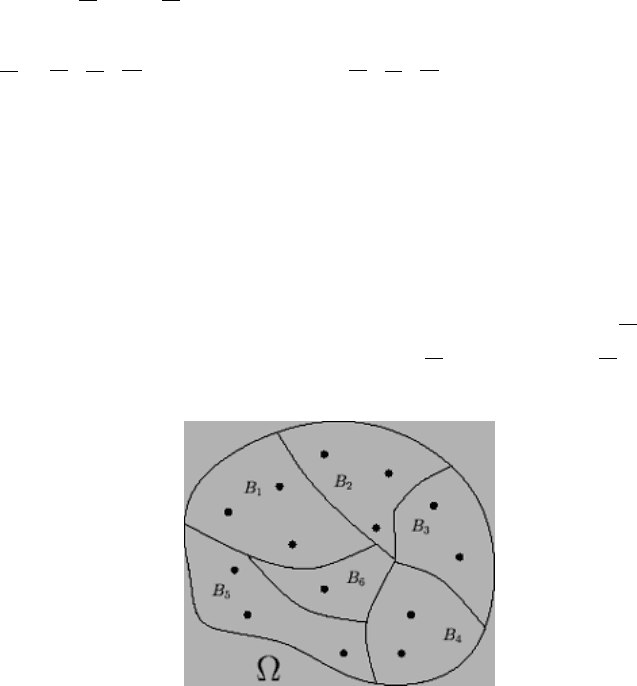
Определение 1.6. Набор событий B
1
, … , B
n
называется полной группой не-
совместных событий
или разбиением пространства Ω, если
Ω=
∑
=
n
i
i
B
1
и ji ≠∀
∅
=
ji
BB I .
Очевидно, что любые два противоположных события
A и
A
образуют пол-
ную группу несовместных событий, т.е.
1)()()()(
=
Ω=
+
=
+
PAPAPAAP
.
Рис 1.7. Разбиение пространства Ω.
Предложение 1.5. (Формула полной вероятности). Пусть события
B
1
, … , B
n
образуют разбиение. Тогда .
∑
=
=
n
i
ii
BPBAPAP
1
)()/()(
Доказательство. Справедливо представление
n
ABABA ++
=
K
1
. Следова-
тельно,
. Для завершения доказательства достаточ-
но применить формулу произведения вероятностей (1.4).
)()()(
1 n
ABPABPAP ++= K
21

Предложение 1.6. (Формула Байеса). Пусть B
1
, … , B
n
– разбиение. Тогда
∑
=
=
n
i
ii
kk
k
BPBAP
BPBAP
ABP
1
)()/(
)()/(
)/(
. #
Замечание 1.5. События, образующие разбиение пространства Ω в форму-
лах полной вероятности и Байеса часто называют
гипотезами и обозначают H
i
.
Пример 1.13. Есть три завода, производящих одну и ту же продукцию. При
этом 1-й завод производит 25%, 2-й завод
− 35% и 3-й завод − 40% всей произ-
водимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от про-
дукции 2-го и 4% от продукции 3-го завода.
Вся продукция смешивается и поступает в продажу. Найти: а) вероятность
купить бракованное изделие; б) условную вероятность того, что купленное из-
делие изготовлено 1-м заводом, если это изделие бракованное.
Решение. Обозначим событие A – «куплено бракованное изделие». Так как
производят продукцию три завода, то выдвинем три гипотезы:
H
1
– изделие изготовлено первым заводом;
H
2
– изделие изготовлено вторым заводом;
H
3
– изделие изготовлено третьим заводом.
Найдем вероятности гипотез: P(H
1
) = 0,25; P(H
2
) = 0,35; P(H
3
) = 0,4. Проверим:
P(H
1
) + P(H
2
) + P(H
3
) = 0,25 + 0,35 + 0,4 = 1.
Найдем условные вероятности события
A относительно выдвинутых гипотез:
P(A/H
1
) = 0,05; P(A/H
1
) = 0,03; P(A/H
1
) = 0,04.
Определим вероятность события
A по формуле полной вероятности:
039,04,004,035,003,025,005,0)()/()(
1
=⋅+⋅+⋅==
∑
=
n
i
ii
HPHAPAP .
Вычислим долю первого завода в общем количестве бракованных изделий,
т.е. переоценим гипотезу
H
1
по формуле Байеса:
321,0
039,0
25,005,0
)(
)()/(
)()/(
)()/(
)/(
11
3
1
11
1
=
⋅
===
∑
=
AP
HPHAP
HPHAP
HPHAP
AHP
i
ii
.
Пример 1.14. Турист, заблудившись в лесу, вышел на полянку, от которой
в разные стороны ведут 5 дорог. Если он пойдет по первой дороге, то вероят-
ность выхода из леса в течение часа равна 0,6; если по второй – 0,3; если по
третьей – 0,2; если по четвертой – 0,1; если по пятой – 0,1. Какова вероятность
того, что турист пошел по первой
дороге, если через час он вышел из леса?
Решение. В данном случае событие A – «турист через час он вышел из ле-
са» произошло. Поэтому используем формулу Байеса. Искомая вероятность то-
го, что турист пошел по первой дороге, если через час он вышел из леса, равна
∑
=
=
5
1
11
1
)/()(
)/()(
)/(
i
ii
HAPHP
HAPHP
AHP
,
где
H
i
– гипотеза «турист пойдет по i-й дороге, i = 1, 2, 3, 4, 5. Очевидно, что
все пять гипотез равновероятны, т.е.
2,0)()()()()(
54321
=
=
=== HPHPHPHPHP .
22

Значения условных вероятностей даны в условии задачи:
1,0)/()/(;2,0)/(;3,0)/(;6,0)/(
54321
=
=
=
=
= HAPHAPHAPHAPHAP .
Отсюда имеем:
=
⋅+⋅+⋅+⋅+⋅
⋅
=
1,02,01,02,02,02,03,02,06,02,0
6,02,0
)/(
1
AHP
462,0
3,1
6,0
1,01,02,03,06,0
6,0
==
++++
=
.
1.10. Независимость событий
Определение 1.7. События A и B называются независимыми, если
)()()(
B
P
A
P
A
B
P
⋅= .
Замечание 1.6. Если A и B независимы и P(B) > 0, то
)(
)(
)()(
)(
)(
)/( AP
BP
BPAP
BP
ABP
BAP ===
.
Аналогично, если A и B независимы и P(A)
> 0, то
)()
/
( B
P
A
B
P
=
.
Пример 1.15. Бросание двух игральных костей:
Ω = {(a
1
, a
2
): a
1
, a
2
∈ {1, … , 6}}, |Ω| = 36,
A = {на первой кости выпала «6»},
B = {на второй кости выпала «6»},
A = {(6, 1), (6, 2), … , (6, 6)}, |A| = 6,
B = {(1, 6), (2, 6), … , (6,
6)}, |B| = 6,
AB = {(6,
6)}, |AB| = 1.
6
1
36
6
)( ==
Ω
=
A
AP ,
6
1
36
6
)( ==
Ω
=
B
BP ,
36
1
)( =
Ω
=
AB
ABP .
Таким образом,
)()()( B
P
A
P
A
B
P
⋅
=
, и события A и B – независимы.
Пример 1.16. Студент сдает три экзамена. Вероятность успешной сдачи
первого экзамена 0,9, второго – 0,65, третьего – 0,35. Найти вероятность того,
что он не сдаст хотя бы один экзамен.
Решение. Обозначим A – событие «студент не сдал хотя бы один экзамен».
Тогда
)(1)( APAP −= ,
где
A
– противоположное событие «студент сдал все экзамены».
Поскольку сдача каждого экзамена не зависит от других экзаменов, то
7953,035,065,09,01)(1)(
=
⋅
⋅−=−= APAP .
Предложение 1.7. Известно, что события A и B независимы. Тогда:
A
и B.
– независимы, A и
B – независимы,
A
и B – независимы.
23

Предложение 1.8. Если события A и B несовместны, то они независимы,
если и только если P(A) = 0 или P(B) = 0.
1.11. Статистическая независимость
Теперь распространим понятие независимости на случай произвольного
конечного набора событий A
1
, … , A
n
. Обсудим два способа распространения
определения 1.7 – понятия взаимной независимости и попарной независимости.
Определение 1.8. События A
1
, … , A
n
называются независимыми в совокуп-
ности (взаимно независимыми), если для всех k (1 ≤ k ≤ n) и для любых
1 ≤ i
1
< … < i
k
≤ n верно
)()()(
11 kk
iiii
APAPAAP KK = . (1.5)
24
)
Определение 1.9. События A
1
, … , A
n
называются попарно независимыми,
если
.
ji ≠∀ ()()(
jiji
APAPAAP ⋅=
Замечание 1.7. Понятия взаимной независимости и попарной независимо-
сти набора событий не являются равносильными, а именно,
Первая импликация вытекает из определений 1.8 и 1.9, достаточно взять в
равенстве (1.5) n = 2. Следующие два примера показывают, что события могут
быть попарно независимыми, но зависимыми в совокупности.
Пример 1.17. Производится бросание двух костей. Рассмотрим события:
A = {на первой кости выпало нечетное число очков},
B = {на второй кости выпало нечетное число очков},
C = {сумма очков – нечетна}.
События A, B, C – попарно независимые. Действительно,
2
/
1)()()( === C
P
B
P
A
P
,
4
/
1)()()(
=
=
=
BC
P
A
C
P
A
B
P
.
Но независимости в совокупности нет, т.к.
)()()(
8
1
0)( CPBPAPABCPABC =≠=⇒∅=
.
Глава 2. Дискретные случайные величины
Для дальнейшего изложения необходимо ввести понятие дискретного ве-
роятностного пространства. Мы будем называть дискретным вероятностным
пространством либо конечное вероятностное пространство, определенное в
§ 1.2, либо счетное вероятностное пространство, которое мы определим ниже.

2.1. Счетное вероятностное пространство
Пусть Ω – счетное множество, то есть, бесконечное множество, элементы
которого могут быть занумерованы натуральными числами:
Niin ∈
ω=
ω
ωω=Ω }{,...},...,,{
21
,
а функция P, зависящая от ω ∈ Ω, удовлетворяет условиям:
0)( ≥ω
P
, .
∑∑
Ω∈ω
∞
=
=ω=ω 1)()(
1i
i
PP
В этом случае говорят, что (Ω, P) – счетное вероятностное пространство.
Как и прежде, событиями будем называть любые подмножества множест-
ва элементарных исходов Ω: A ⊆ Ω.
2.2. Дискретные случайные величины
Определение 2.1. Случайной величиной назовем произвольную функцию на
множестве элементарных исходов: ξ: Ω → R, ξ = ξ(ω). Случайные величины
обозначают греческими или заглавными латинскими буквами.
Множества вида {ω: ξ(ω) = x} ⊆ Ω являются событиями. Далее для них бу-
дем использовать более короткое обозначение:
})(:{}{
x
x
=ωξ
ω
=
=
ξ
&
.
Так как Ω – не более чем счетно, то случайная величина ξ принимает не
более чем счетное число значений: x
1
, x
2
, … , x
k
, … .
Определение 2.2. Распределением дискретной случайной величины ξ назо-
вем таблицу
ξ
x
1
x
2
…
x
k
…
P
p
1
p
2
…
p
k
…
где }{})(:{
kkk
xPxPp
=
ξ=
=
ωξω= .
Замечание 2.1. Если k ≠ l, то {ξ = x
k
} ∩ {ξ = x
l
} = ∅. Более того,
Ω==ωξω
U
k
k
x })(:{
. Следовательно,
1
=
∑
k
k
p
.
2.3. Схема Бернулли
2.3.1. Распределение числа успехов в n испытаниях
Определение 2.3. Схемой Бернулли называется последовательность незави-
симых испытаний, в каждом из которых возможны лишь два исхода – «успех»
и «неудача», при этом «успех» в одном испытании происходит с вероятностью
р ∈ [0, 1], «неудача» – с вероятностью q = 1 – р.
25
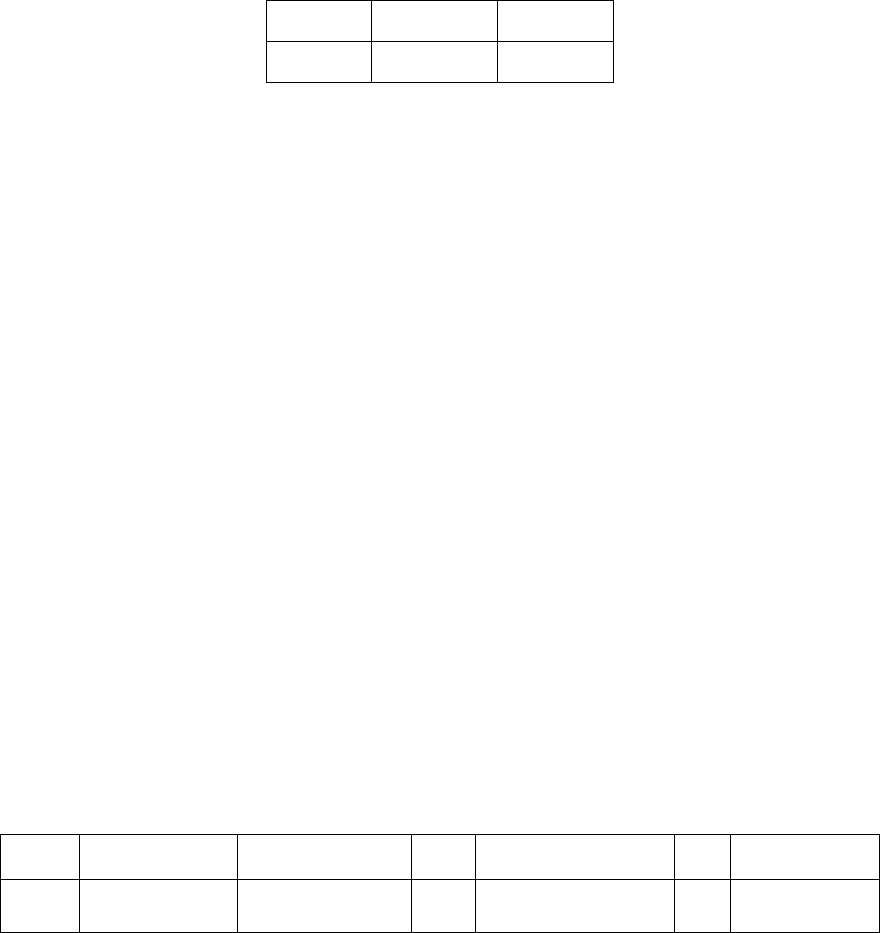
Определение 2.4. Бернуллиевской называют случайную величину, прини-
мающую два значения:
с вероятностью p,
⎩
⎨
⎧
=ξ
,0
,1
i
с вероятностью 1 –
p.
Таким образом, ее распределению соответствует таблица
ξ
0 1
P
1 − p
p
Предложение 2.1. (Формула Бернулли). Обозначим, через v
n
число успехов
в
n испытаниях схемы Бернулли. Тогда для любого k = 0, 1, ... , n
knkk
n
knkk
nnn
qpCppCkPkvP
−−
=−=== )1()()(.
Доказательство. Событие А = {v
п
= k} означает, что в п испытаниях схемы
Бернулли произошло ровно k успехов (и, соответственно, (n − k) неуспехов).
Рассмотрим один из благоприятствующих событию A элементарных исходов:
(
.
43421321
klk
nnnuuu
−
,....,,,...,)
Т.к. испытания независимы, вероятность такого элементарного исхода (первые
k испытаний завершились успехом, остальные неудачей) равна p
k
(1−p)
n
−
k
. Дру-
гие благоприятствующие событию A элементарные исходы отличаются от рас-
смотренного выше лишь расположением k успехов на n местах. Есть ровно C
n
k
способов расположить k успехов на n местах. Поэтому событие A состоит из C
n
k
элементарных исходов, вероятность каждого из которых равна p
k
(1−p)
n
−
k
.
Определение 2.5. Набор чисел P(v
n
= k) = C
k
p
k
(1−p)
n
−
k
, k = 0, 1, … ,n назы-
вается биномиальным распределением вероятностей и обозначается B
n,p
или
B(n, p). Случайную величину с этим законом распределения называют биноми-
альной. Она означает, что в п испытаниях схемы Бернулли произошло ровно k
успехов и (n−k) неуспехов.
Биномиальному распределению вероятностей соответствует таблица
ν
n
0 1
…
k
…
n
P
n
p)1( −
1
)1(
−
−
n
pnp
…
knkk
n
ppC
−
− )1(
…
n
p
Пример 2.1. В магазине 5 холодильников. Вероятность выхода из строя
каждого холодильника в течение года равна 0,2. Найти вероятность того, что в
течение года ремонта потребует: 1) 4 холодильника; 2) не менее 2 холодильни-
ков; 3) не более 1 холодильника; 4) не менее 1 холодильника.
Решение. Поскольку все холодильники имеют одинаковую вероятность
выхода из строя в течение года p = 0,2, то используем формулу
Бернулли.
1) Вероятность того, что в течение года ремонта потребуют 4 холодильни-
ка, равна
0064,08,02,05)1()4(
444
55
=⋅⋅=−== ppCkP .
26

2) Вероятность того, что в течение года ремонта потребуют не менее 2 хо-
лодильников, равна
=
=
−
=
−
=<−=≥ )1()0(1)2(1)2(
5555
kPkPkPkP
2627,08,02,058,02,011)1()1(1
4150411
5
500
5
=⋅⋅−⋅⋅−=−−−−= ppCppC .
3) Вероятность того, что в течение года ремонта потребует не более 1 хо-
лодильника, равна
7373,02627,01)2(1)1(
55
=
−
=≥−=≤ kPkP .
4) Вероятность того, что в течение года ремонта потребует не менее 1 хо-
лодильника, равна
=
=
−
=<−=≥ )0(1)1(1)1(
555
kPkPkP
6723,0
100000
67232
8,02,011)1(1
50500
5
==⋅⋅−=−−= ppC .
Пример 2.2. Вероятность того, что изделие является дефектным, равна 0,1.
Сколько надо выбрать изделий, чтобы среди них с вероятностью более 0,96
оказалось хотя бы одно бездефектное?
Решение. По условию задачи требуется найти минимальное число n, для
которого выполнялось бы неравенство
. Данное неравенство
равносильно тому, что
.
96,0)1( >≥kP
n
04,096,01)0(
00
=−<== qpCkP
n
nn
Подставив 9,0
=
p
, в последнее неравенство, и, учтя, что ,
имеем:
.
1,0=q 1
0
=
n
C
04,09,01,09,01)0(
000
<=⋅⋅===
nnn
nn
qpCkP
Прологарифмируем обе части полученного неравенства:
04,0ln9,0ln >n ⇒
551,30
1054,0
2189,3
9,0ln
04,0ln
=
−
−
=>n
⇒ . 31
min
=n
Таким образом, надо выбрать не менее чем 31 изделие, чтобы среди них с
вероятностью более 0,96 оказалось хотя бы одно бездефектное
Пример 2.3. Адвокат выигрывает в суде в среднем 70% дел. Найдите веро-
ятность того, что он из 8 дел выиграет больше половины.
Решение. По условию задач требуется определить вероятность ,
где
k – количество выигранных дел.
)4(
8
>kP
Поскольку вероятность выигрыша дела известна (7,0
=
p
), то
3,01
=−=
p
q . Отсюда по формуле Бернулли имеем:
=
=
+
=
+
=
+==> )8()7()6()5()4(
88888
kPkPkPkPkP
=⋅⋅+⋅⋅+⋅⋅+⋅⋅=
088
8
177
8
266
8
355
8
3,07,03,07,03,07,03,07,0 CCCC
797,00576,01776,02965,02450,0
=
+
++= .
Таким образом, вероятность того, что адвокат из 8 дел выиграет больше поло-
вины, равна 0,797.
27
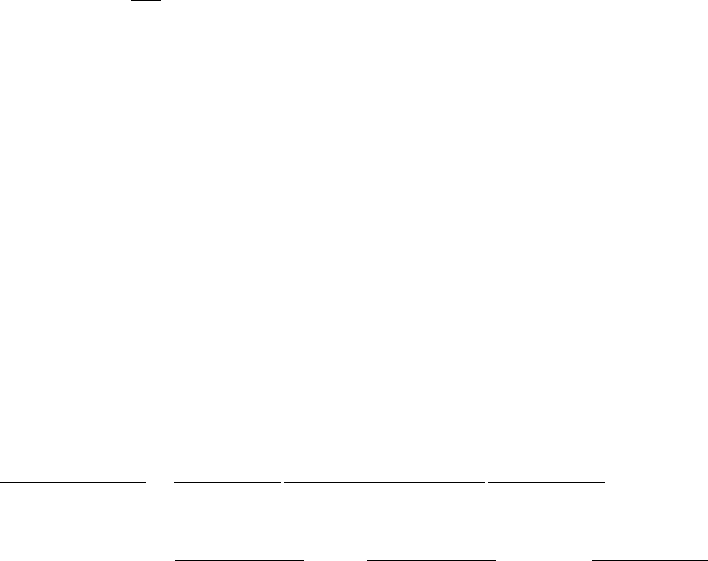
Определение 2.6. Будем говорить, что случайная величина Π имеет пуас-
соновское распределение с параметром
λ > 0, если она принимает целые неот-
рицательные значения со следующими вероятностями:
{}
...,1,0,
!
=
λ
==Π
λ−
ke
k
kP
k
.
2.3.2. Наиболее вероятное число успехов
По формуле Бернулли, событие «произошло 0 успехов в п испытаниях»
имеет вероятность
q
n
, 1 успех − вероятность npq
n−1
и т.д. Какое же число успе-
хов
наиболее вероятно, или, при каком k достигается максимум P(v
n
= k)?
Предложение 2.2. В n испытаниях схемы Бернулли с вероятностью успеха
p наиболее вероятным числом успехов является
а) единственное число
k
0
= [np + p], если число np + p не целое;
б) два числа
k
0
= np + p и k
0
= np + p − 1, если число np + p целое.
Доказательство. Чтобы выяснить это, сравним отношение P(v
n
= k) и
P(v
n
= k−1) с единицей:
=
+−−
−
=
−=
=
+−−
−
11
!
)!1()!1(
)!(!
!
)1(
)(
knk
knk
n
n
qp
qp
n
knk
knk
n
kvP
kvP
kq
kpnp
kq
pkn
kq
pkn −
+
+=−
+
−
+=
+−
= 11
)1(
1
)1(
.
Видим, что
(
a) Р(v
n
= k) > Р(v
n
= k − 1) при np + p − k > 0, то есть при k < np + p;
(
b) Р(v
n
= k) < Р(v
n
= k − 1) при np + p − k < 0, то есть при k > np + p;
(
c) P(v
n
= k) = P(v
n
= k − 1) при np + p − k = 0, что возможно лишь если пр + р
− целое число.
Рассмотрим два случая:
пр + р ∈ Z и пр + р ∉ Z. В первом случае пусть
k
0
= пр + р. Из полученных выше неравенств сразу следует, что
...)1()()1()2(...
0
)(
0
)(
0
)(
0
>+=>==−=<−=< kvPkvPkvPkvP
n
b
n
c
n
a
n
Во втором случае пусть
k
0
= [пр + р] (целая часть числа пр + р). Из неравенств
(
а), (b) следует, что
...)1()()1()2(...
0
)(
0
)(
0
)(
0
>+=>=<−=<−=< kvPkvPkvPkvP
n
b
n
a
n
a
n
.
Действительно, неравенство
Р(v
n
= k
0
) > Р(v
n
= k
0
− 1), например, следует из
(b), примененного для
k = k
0
− 1 > np + p.
В зависимости от того, является число
пр + р целым или нет, имеем либо
два равновероятных «наиболее вероятных» числа успехов
k
0
= пр + р и
k
0
− 1 = пр + р − 1, либо одно «наиболее вероятное» число успехов, равное
k
0
= [пр + р].
Замечание 2.2. В предложении 2.2 наиболее вероятное число успехов k
0
можно находить из двойного неравенства
pnpkqnp +
≤
≤
−
0
.
28
Пример 2.4. Если p = q = 1/2, то при четном числе испытаний n число
np + р = (п+1)/2 ∉ Z − не целое, так что наиболее вероятным является единст-
венное число успехов [(
п+1)/2] = n/2. Что совершенно понятно, так как есть не-
четное число возможностей – получить 0,1, ... ,
п успехов, причем вероятности
получить
k и п−k успехов одинаковы.
При нечетном же числе испытаний
п число пр + р = (п+1)/2 ∈ Z − целое,
так что наиболее вероятными (и одинаково вероятными) являются два числа
успехов (
п+1)/2 и (п−1)/2.
Пример 2.5. Вероятность появления события A в каждом из n независимых
испытаний равна 0,7. Сколько испытаний нужно произвести, чтобы наиболее
вероятное число появлений события
A в производимых испытаниях
20
0
=
k
?
Решение. По условию
7,0
=
p
и 3,0
=
q . Тогда из замечания 2.2 получим
7,07,0203,07,0 +≤≤− nn .
Это двойное неравенство равносильно системе неравенств
⎩
⎨
⎧
≥+
≤−
.207,07,0
,203,07,0
n
n
Из первого неравенства системы имеем
297,0
/
3,20
=
≤
n . Из первого неравен-
ства системы найдем
57,277,0
/
3,19
≈
≥n . Отсюда следует, что необходимо
произвести 28 или 29 испытаний.
2.3.3. Номер первого успешного испытания
Рассмотрим схему Бернулли с вероятностью успеха p в одном испытании.
Испытания проводятся до появления первого успеха. Введем величину τ, рав-
ную номеру первого успешного испытания.
Предложение 2.3. Вероятность того, что первый успех произойдет в испы-
тании с номером k ∈ N = {1, 2, 3, …}, равна
.
1
)(
−
==τ
k
pqkP
Доказательство. Действительно,
1
1
),,,()(
−
−
===τ
k
k
pqunnnPkP
43421
K
Определение 2.7. Набор чисел называется геометриче-
ским распределением вероятностей и обозначается G(p).
...},3,2,1,{
1
=
−
kpq
k
Геометрическое распределение вероятностей обладает интересным свойст-
вом «нестарения», заключающимся в следующем. Пусть величина τ обозначает
время безотказной работы (измеряемое целым числом часов) некоторого уст-
ройства. Предположим, что для величины τ вероятность принять любое свое
значение k равна pq
k−l
, т.е. P(τ = k) = рq
k−l
для любого k ∈ N. Тогда для произ-
вольных n, k ≥ 0
)()
/
(
k
P
n
k
n
P
>τ=>τ+>τ . (2.1)
29
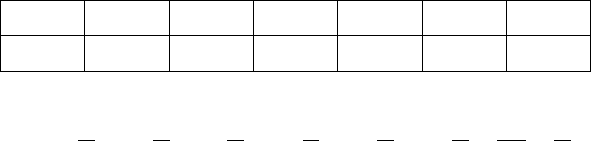
Формула (2.1) означает следующее. Если известно, что устройство уже прора-
ботало без отказа n часов, то вероятность ему работать еще не менее k часов та-
кая же, как вероятность проработать не менее k часов для нового устройства.
2.4. Математическое ожидание
Так как случайная величина ξ может принимать различные значения ξ(ω),
в зависимости от того, какой исход ω «виртуального» эксперимента (замеча-
ние 1.1) будет разыгран, то с разных точек зрения удобно иметь числовую ха-
рактеристику, имеющую смысл «среднего значения» случайной величины.
Определение 2.8. Математическим ожиданием дискретной случайной ве-
личины ξ называется число
∑
Ω∈ω
ω
ω
ξ
=
ξ
)()(][ PM
.
Математическое ожидание существует в том и только в том случае, когда
этот ряд сходится абсолютно.
Предложение 2.4. Математическое ожидание может быть вычислено как
∑∑
=
ξ==ξ
kk
kkkk
xPxpxM }{][
. (2.2)
Доказательство. Мы будем использовать следующий факт из курса мате-
матического анализа. Пусть дан абсолютно сходящийся ряд. Тогда его члены
можно произвольным образом переставлять и группировать, полученные в ре-
зультате этого ряды будут сходиться к одному и тому же значению:
∑
∑
∑
=
ω
=ωωξ=ξ
=ωξωΩ∈ω kx
k
k
PxPM
)(:
)()()(][
∑∑
∑
=
ω
ξ
ω
=ω=
=ωξω k
kk
kx
k
xPxPx
k
})(:{)(
)(:
.
Пример 2.6. Математическое ожидание бернуллиевской случайной вели-
чины:
ppp
M
=−⋅
+
⋅=ξ )1(01][
.
Пример 2.7. ξ – число очков, выпавших на игральной кости. Распределение
этой случайной величины:
ξ
1 2 3 4 5 6
P
1/6 1/6 1/6 1/6 1/6 1/6
2
7
6
21
6
1
6
6
1
5
6
1
4
6
1
3
6
1
2
6
1
1][ ==⋅+⋅+⋅+⋅+⋅+⋅==ξ
∑
k
k
kpM
.
Пример 2.8. Пусть случайная величина ξ имеет биномиальное распределе-
ние. Найдем ее математическое ожидание. Согласно (2.2) имеем
knk
n
k
k
n
qpkCM
−
=
∑
=ξ
0
][
.
30
