Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие

Подождите немного. Документ загружается.

РАЗДЕЛ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Теория вероятностей – математическая наука, изучающая закономерно-

сти случайных явлений. Случайным называют эксперимент, результат которо-

го нельзя предсказать заранее. Невозможность предсказать заранее – основное,

что отличает случайное явление от детерминированного.

Очевидно, что в экономике, как и в природе и технике, нет явлений, в ко-

торых отсутствовали бы элементы случайности. Знание закономерностей, кото-

рым подчиняются массовые случайные явления, позволяет предвидеть, как эти

явления будут протекать. Причем результат, развитие явления определяется как

основными факторами, так и второстепенными

, приводящими к случайным ис-

кажениям результата, т.е. вносящими в него элемент неопределенности. Эта

неопределенность, свойственная случайным явлениям, требует специальных

методов их изучения. Разработкой таких методов, изучением закономерностей,

наблюдаемых в случайных явлениях, и занимается теория вероятностей.

Не все случайные явления (эксперименты) можно изучать методами тео-

рии вероятностей, а лишь те, которые могут быть воспроизведены в одних и

тех же условиях и обладают (непонятно как проверяемым заранее) свойством

«статистической устойчивости»: если A – некоторое событие, могущее про-

изойти или не произойти в результате эксперимента, то доля n(А)/n числа экс-

периментов, в которых данное событие произошло, имеет тенденцию стабили-

зироваться с ростом общего числа экспериментов n, приближаясь к некоторо-

му числу P(А) – вероятности события A. Это число служит объективной ха-

рактеристикой «степени возможности» событию A произойти.

В дальнейшем мы будем говорить лишь о случайных явлениях, обладаю-

щих данными свойствами.

Глава 1. События и их вероятности

1.1. Определение понятия «вероятность»

Наибольшую трудность при изучении теории вероятностей представляет

принятие удовлетворительного определения вероятности. Наибольшее распро-

странение в настоящее время получили два подхода к определению вероятно-

сти – относительно-частотный и аксиоматический. Первый из них основан на

придании понятию «вероятность» некоторого физического смысла. Решения в

этом случае выполняются путем обращения к концепции относительной часто-

ты события. Ограничение данного подхода заключается в сложности его ис-

пользования в случаях, слишком трудных для анализа с точки зрения их физи-

ческого или экономического обоснования.

В аксиоматическом подходе вероятность события трактуется как некая

численная величина, удовлетворяющая определенным постулатам, но более

никак не определяется. Вопрос о том, соотносится ли она с

явлениями реально-

го мира или нет, не является поводом для размышлений при развитии матема-

тических построений, отправной точкой которых служат принятые постулаты.

Независимо от того, какие экономические величины обозначаются абстракт-

ными математическими символами, возникает та же математическая модель.

Задача экономиста состоит в выборе такого способа соотнесения математиче-

ской модели и явлений реального мира

, чтобы получить хотя и приближенные,

но полезные решения практических задач.

Из приведенных рассуждений следует, что наиболее подходящим для эко-

номических приложений подходом к определению вероятности должен быть

двунаправленный подход, при котором понятие относительной частоты неко-

торого случайного события используется для соотнесения простых результатов

с физической реальностью, а аксиоматический подход – для

получения матема-

тических описаний, соответствующих более сложным ситуациям.

1.2. Конечное вероятностное пространство

Рассмотрим произвольное конечное множество Ω = {ω

, … , ω

}, которое

впредь будем называть множеством элементарных исходов, а его элементы ω

– элементарными исходами. Число элементов множества Ω обозначим

Ω

. Оче-

видно, что

K=Ω . Пусть задана функция

]1,0[: →

Ω

. То есть, каждому эле-

ментарному исходу

ω поставлено в соответствие число P(ω) из отрезка [0, 1].

Будем предполагать, что

1)()(

=ω=ω

∑∑

Ω∈ω

PP . (1.1)

Функцию P, удовлетворяющую этим свойствам, назовем вероятностью на Ω.

Определение 1.1. Пару (Ω, P), составленную из множества Ω и функции P,

удовлетворяющих перечисленным выше требованиям, называют конечным ве-

роятностным пространством.

Пример 1.1. (Вероятностное пространство с равновероятными элемен-

тарными исходами). Производится бросание двух игральных костей, изготов-

ленных из однородного материала и имеющих правильную форму. Элементар-

ным исходом служит упорядоченная пара чисел

),( ji

, где i – число очков

на первой кости, j – число очков на второй кости. Множество элементарных ис-

ходов можно задать перечислением:

Ω = {(1,

1), (1,

2), …, (1,

6), (2,

1), …, (2,

6), …, (6,

1), …, (6,

6)}.

Очевидно, что

Ω . Вероятность можно задать как: ∀ω 361)( =ωP .

Пример 1.2. Монета подбрасывается до тех пор, пока не выпадет вверх

гербом. Пространство элементарных исходов состоит из бесконечного, но счет-

ного числа исходов: Ω = {г, рг, ррг, рррг, ррррг, рррррг, ... }, где р и г обознача-

ют выпадение решки и герба при одном подбрасывании, соответственно.

Пример 1.3. На поверхность стола бросается монета. Результатом экспе-

римента можно считать координату центра монеты (а если нам не безразличен

угол поворота монеты, то можно добавить и величину этого угла). Пространст-

во элементарных исходов — множество точек стола (в втором случае – множе-

ство пар {(x, ϕ)}, где x ∈ R

– точка стола и (р ∈ [0,

2π) – угол поворота). Число

элементарных исходов такого эксперимента несчетно.

1.3. Случайные события

Определение 1.2. Произвольные подмножества

Ω

⊆

множества элемен-

тарных исходов называются событиями. Пустое множество ∅ называется не-

возможным событием, все множество Ω

−

достоверным событием. Любое со-

бытие, состоящее из одного элемента, называется элементарным.

Иными словами, событие – это всякий факт, который в результате опыта

может произойти или не произойти. Под испытанием (опытом) понимается

осуществление некоторого комплекса условий. Событие в опыте называется

случайным, если при повторениях опыта оно иногда происходит, иногда нет.

Случайные события

обозначаются A, B, C и т.д. События в опыте называются

равновозможными, если условия их появления одинаковы и нет оснований

считать какое-либо из них более возможным, чем любое другое.

Пример 1.4. Опыт - бросание игральной кости; события:

– выпадение одного очка,

– выпадение двух очков,

– выпадение трех очков,

– выпадение четырех очков,

– выпадение пяти очков,

– выпадение шести очков,

В – выпадение четного числа очков,

С – выпадение более семи очков,

D – выпадение не более шести.

Достоверное событие в данном опыте – D, невозможное – С, остальные со-

бытия – случайные. События А

, А

не могут быть выражены через

более простые события и являются элементарными событиями (элементарными

исходами). Кроме того, они образуют полную группу равновозможных собы-

тий. Событие B не является элементарным, т.к. его можно выразить через более

простые события: либо наступит А

, либо наступит А

, либо А

Определение 1.3. Вероятностью события A называется число

. Зафиксируем некоторое подмножество

. Если

исход эксперимента ω принадлежит A, то говорят, что произошло событие

A, если

∑

∈ω

ω=

PAP )()(

},,{

1 K

A ωω⊆ K

∉ω , то говорят, что событие A не произошло.

Пример 1.5. Бросание двух игральных костей. Рассмотрим события:

A = {(1,5), (2,4), (3,3), (4,2), (5,1)} и B = A ∪ {(6,6)}.

Словами эти события можно описать следующим образом:

A = {суммарное число очков равно 6},

B = {суммарное число очков делится на 6}.

Очевидно, что P(A) = 5/36, P(B) = 1/6.

Замечание 1.1. Для того чтобы любая проблема могла изучаться математи-

ческими методами, вначале ее необходимо формализовать или, как принято го-

ворить, построить ее математическую модель. В данном случае задача сводится

к выбору вероятностного пространства. Замечательно то, что, изучая строгие

математические модели, мы, тем не менее, можем использовать нашу жизнен-

ную интуицию и «

здравый смысл». Этому способствует язык теории вероятно-

стей, перекидывающий мостик между теоретико-множественными конструк-

циями и привычной обиходной лексикой.

При построении вероятностных пространств, соответствующих реальным

практическим задачам, полезно держать в голове следующую схему. Имеется

некоторый «виртуальный» (то есть, воображаемый) эксперимент, возможные

исходы которого (

, … , ω

). Эксперимент завершается только одним исходом

, который заранее нельзя предугадать в точности.

1.4. Операции над событиями

Рассмотрим теперь, как язык теории вероятностей трактует теоретико-

множественные операции.

Если

A – событие, то его теоретико-множественное дополнение

}:{\ AAA ∉ωω=Ω=

тоже есть событие

, называемое отрицанием (или противоположным собы-

тием) события A. Событие

происходит тогда и только тогда, когда не проис-

ходит событие A.

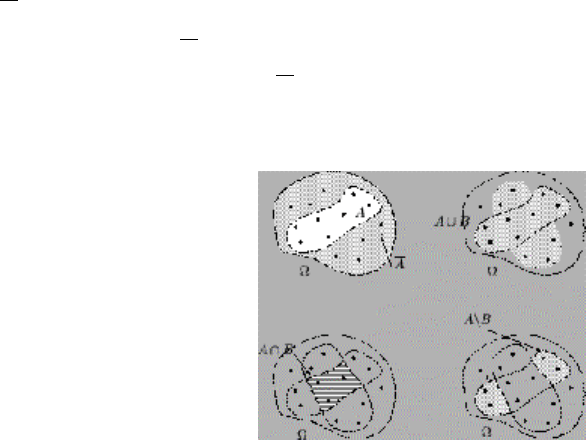
Рис. 1.1. Операции над событиями: отрицание, объединение, пересечение и

разность.

Если A и B – события (A, B ⊆ Ω), то A ∪ B, A ∩ B и A \ B – также события,

которые можно описать следующим образом:

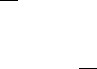
1) Объединение (или сумма) событий A ∪ B = A + B {произошло хотя бы одно

из событий A или B}, очевидно, что A ∪

= Ω.

2) Пересечение (или произведение) событий A ∩ B = A

⋅

B = AB {одновременно

происходят события A и B}, очевидно, что A ∩

= ∅.

3) Разность событий A \ B = A – B {произошло событие A, но не произошло B}.

Если A ∩ B = ∅, то говорят, что A и B несовместны (не могут произойти

одновременно). В противном случае они являются совместными.

Пример 1.6. Победитель конкурса награждается медалью (событие A),

премией (событие B), призом (событие C). Что представляют собой события:

а) A + B; б) ABC; в) AC – B?

Решение. а) Событие A + B состоит в награждении победителя или меда-

лью, или премией, или и тем, и другим.

б) Событие ABC состоит в награждении победителя

одновременно и меда-

лью, и премией, и призом.

а) Событие AC – B состоит в награждении победителя одновременно и ме-

далью, и призом без выдачи премии.

1.5. Простейшие свойства вероятностей

В данном параграфе мы покажем, какие свойства вероятности P имеют ме-

сто по отношению к только что введенным операциям над событиями.

Предложение 1.1. Пусть A и B – некоторые события, т.е. A, B ⊆ Ω. Имеют

место следующие свойства:

1) 0 ≤ P(A) ≤ 1, P(∅) = 0, P(Ω) = 1;

2) Если AB = ∅, то P(A∪B) = P(A+B) = P(A) + P(B);

3) Если AB ≠ ∅, то P(A∪B) = P(A

) + P(B) – P(AB).

Доказательство. ∀ω P(ω) ≥ 0 ⇒

∑

Ω∈ω

≥

0)()( PAP

Очевидно,

В случае, когда AB = ∅,

.1)()( =ω≤ω

∑∑

Ω∈ω∈ω

∑

∈ω∈ω∪∈ω

=ω=∪

ABBA

BPAPPPPBAP )()()()()()(

В общем случае имеет место представление: A∪B = (A\B) + (B\A) + AB.

Следовательно,

∑

∈ω∈ω∈ω

=∪

ABABBA

PPPBAP )()()()(

. Заметим, что

A = (A\B) + AB. Следовательно, по свойству 2

P(A) = P(A\B) + P(AB) ⇒ P(A\B) = P(A) − P(AB).

Аналогично, P(B\A) = P(B) − P(AB). Итак,

P(A∪B) = P(A\B) + P(B\A) + P(AB) =

= (P(A) − P

(AB)) + (P(B) − P(AB)) + P(AB) = P(A) + P(B) − P(AB). 

Предложение 1.2. (Теорема сложения вероятностей). Пусть A

, … , A

–

события. Тогда справедливы утверждения:

1. Если ∀ i

≠

j A

= ∅, то P(A

+ … + A

) = P(A

) + … + P(A

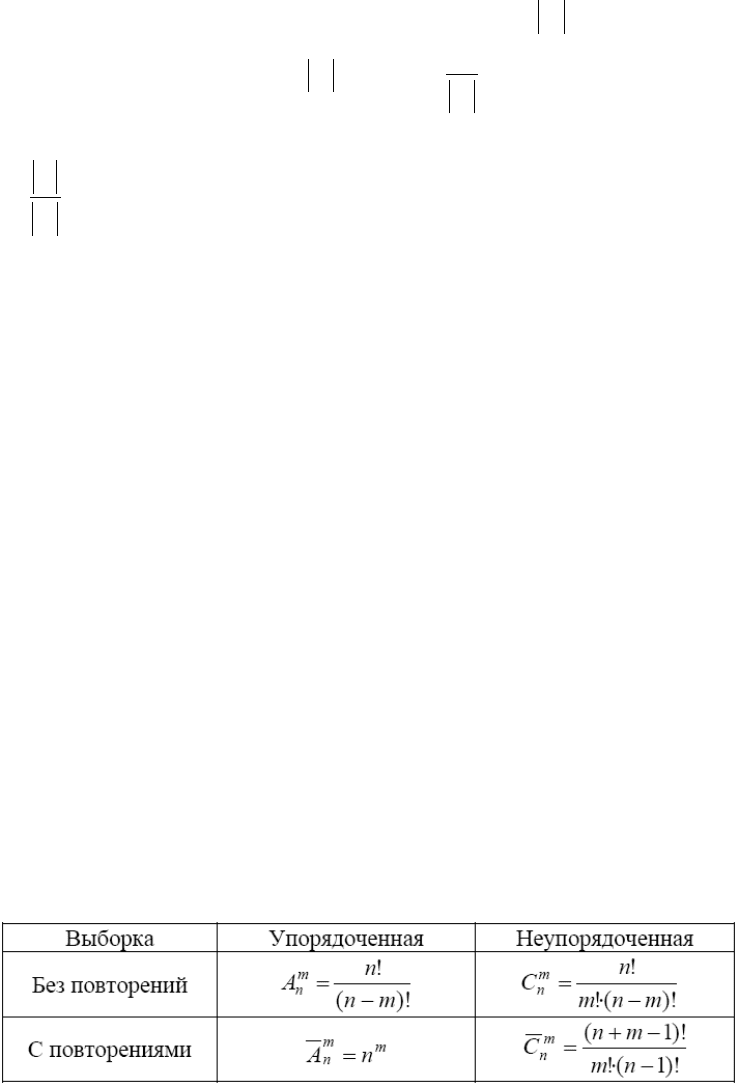
2. В общем случае справедливо равенство

∑∑

+−=∪∪

)()()(

AAPAPAAP K

. #

∑

−

−+−+

321

)()1()(

iii

AAPAAAP KK

1.6. Классическое определение вероятности

Под классическим определением вероятностей подразумевают выбор та-

кого конечного вероятностного пространства, в котором все элементарные ис-

ходы равновероятны: |Ω| < ∞, ∀ω

≠ ω

P(ω

) = P(ω

Покажем, что тогда с необходимостью

Ω

/1)(P . Действительно, пусть

∀ω P(ω) = a. Имеем

Ω

∑

Ω∈ω

aP )(1

⇒

Ω

a .

Следовательно, вероятность любого события

},...,{

1 K

равна

Ω

AP )( , (1.2)

которая читается так: вероятность события есть отношение числа благопри-

ятных исходов к общему числу исходов.

Замечание 1.2. Отметим, что формула (1.2) справедлива только для случая,

когда все исходы ω

равновероятны и образуют полную группу событий.

Замечание 1.3

Мы видим теперь, что подсчет вероятности в класси-

ческой схеме сводится к подсчету числа «шансов» (элементарных исхо-

дов), благоприятствующих какому-либо событию, и общего числа шансов.

Как правило, это делается с помощью формул комбинаторики.

1.6.1. Элементы комбинаторики

Имеется совокупность n объектов, назовем ее генеральной совокупностью.

Из генеральной совокупности наудачу отбираем m объектов, эту отобранную

совокупность назовем выборкой.

Выборка может быть упорядоченной, если порядок элементов играет роль,

и может быть неупорядоченной, если порядок элементов роли не играет.

Выборка может быть без повторений, если элементы повторяться не могут,

и может

быть с повторениями, если элементы в выборке повторяются.

Таблица 1.1

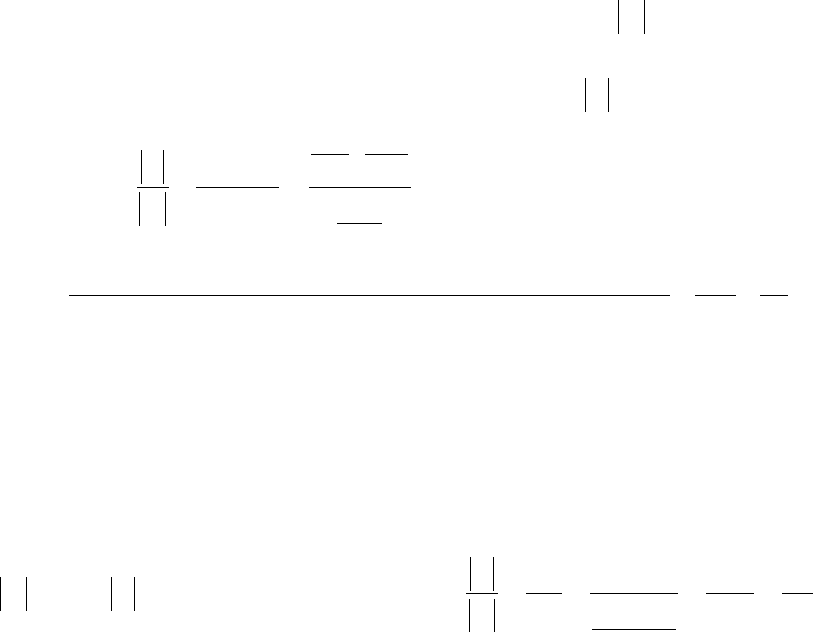
Упорядоченная выборка из n элементов по m называется размещением, не-

упорядоченная выборка из n элементов по m называется сочетанием. Число

размещений и сочетаний с повторениями и без повторений из n элементов по m

можно найти из таблицы 1.1.

Следует запомнить: а) n! = n(n−1)(n−2)…2⋅1; б) 0! = 1.

Предложение 1.3. (Правило произведения). Пусть подсчитывается количе-

ство объектов, каждый из которых строится в результате последовательного

выполнения n действий. Первое действие может быть выполнено а

способами,

второе − а

способами, … , последнее – а

способами, при этом количество

способов выполнить каждое действие не зависит от того, какими были преды-

дущие действия. Тогда общее количество объектов равно а

⋅а

⋅

…⋅а

. #

Пример 1.7. Два счета из десяти выполнены с ошибками. Найти вероят-

ность того, что из четырех взятых на проверку счетов один счет окажется с

ошибками.

Решение. Используем классическую формулу (1.2). Т.к. имеем неупорядо-

ченные выборки без повторений, то всего случаев

C=Ω , из них благоприят-

ных (согласно

предложению 1.3, имеем два действия – выбор 1 счета с ошиб-

ками из двух и выбор 3 правильных счетов из 8)

CCA ⋅= . Следовательно,

⋅

Ω

)(

!6!4

!10

!5!3

!1!1

⋅

)10987654321()54321()321(

)654321()4321()87654321(21

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

⋅

⋅⋅⋅⋅

⋅

⋅⋅⋅⋅

105

Пример 1.8. В комитете из 7 человек нужно выбрать председателя и секре-

таря. Найти вероятность того, что ими окажутся два определенных человека.

Решение. Обозначим через B рассматриваемое событие: B – председателем

и секретарем окажутся два вполне определенных человека.

Воспользуемся классической формулой (1.2) для вычисления вероятности

события

B. Т.к. выборки в данном случае упорядоченные и без повторений, то

==Ω BA , следовательно,

!)27(

)(

⋅

−

Ω

BP .

1.7. Геометрическая вероятность

Рассмотрим некоторую область Ω в R

(на прямой, на плоскости, в про-

странстве). Предположим, что «мера» Ω (длина, площадь, объем, соответствен-

но) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бро-

саем в эту область точку (см. рис. 1.2).

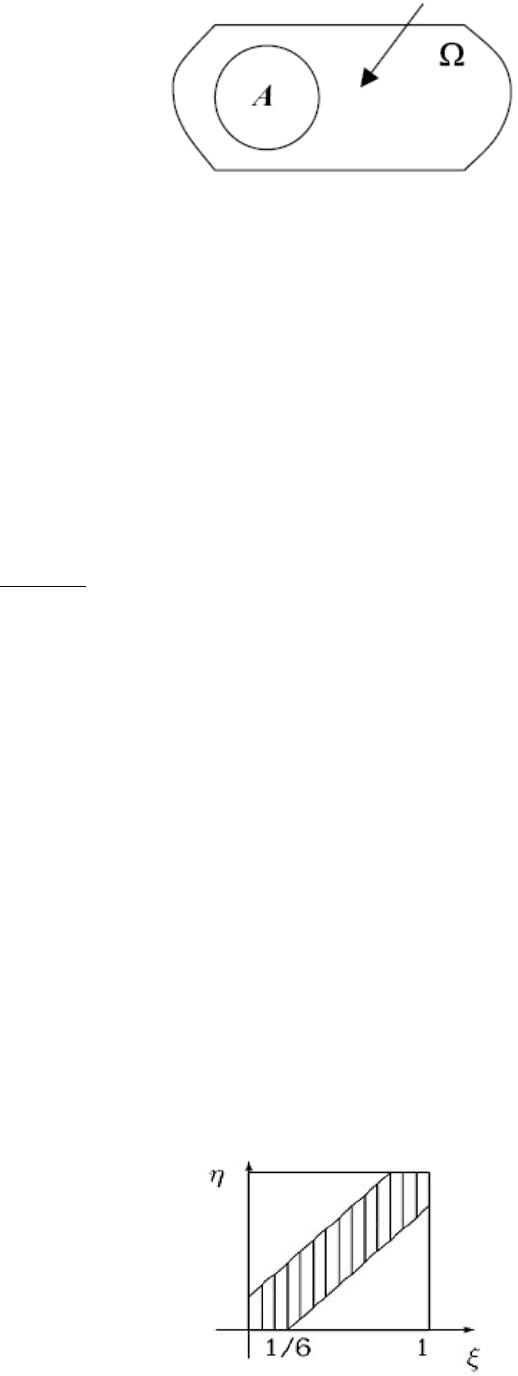
Рис. 1.2.

Термин «наудачу» здесь означает, что вероятность попадания точки в лю-

бую часть A с Ω не зависит от формы или расположения А внутри Ω, а зависит

лишь от «меры» области А (если А измеримо).

Определение 1.4.

Эксперимент удовлетворяет условиям «геометрического

определения вероятности», если его исходы можно изобразить точками неко-

торой области Ω в R

так, что вероятность попадания точки в любую часть

A ⊂ Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от

меры области А и равна:

)mes(

)(

Ω

, (1.3)

где mes(A) – мера области A, благоприятствующей появлению искомого собы-

тия; mes(Ω) – мера области Ω.

«Мерой» мы пока будем называть длину, площадь, объем и т.д. Если для

точки, брошенной в область Ω, выполнены условия геометрического определе-

ния вероятности, то говорят, что точка равномерно распределена в области Ω.

Пример 1.9. (Задача о встрече). Два лица X и Y условились встретиться в

определенном месте между двумя и тремя часами дня. Пришедший первым

ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность

встречи этих лиц, если каждый из них может прийти в любое время в течение

указанного часа независимо от другого

Решение. Будем считать интервал с 14 до 15 часов дня отрезком [0,1] дли-

ной 1 час. Пусть ξ и η − моменты прихода X и Y (точки отрезка [0,1]). Все воз-

можные результаты эксперимента − множество точек квадрата со стороной 1:

Ω = {(ξ, η): 0 ≤ ξ ≤ 1, 0 ≤ η ≤ 1} = [0, 1] × [0, 1], т.е. mes(Ω) = 1.

Рис. 1.3.

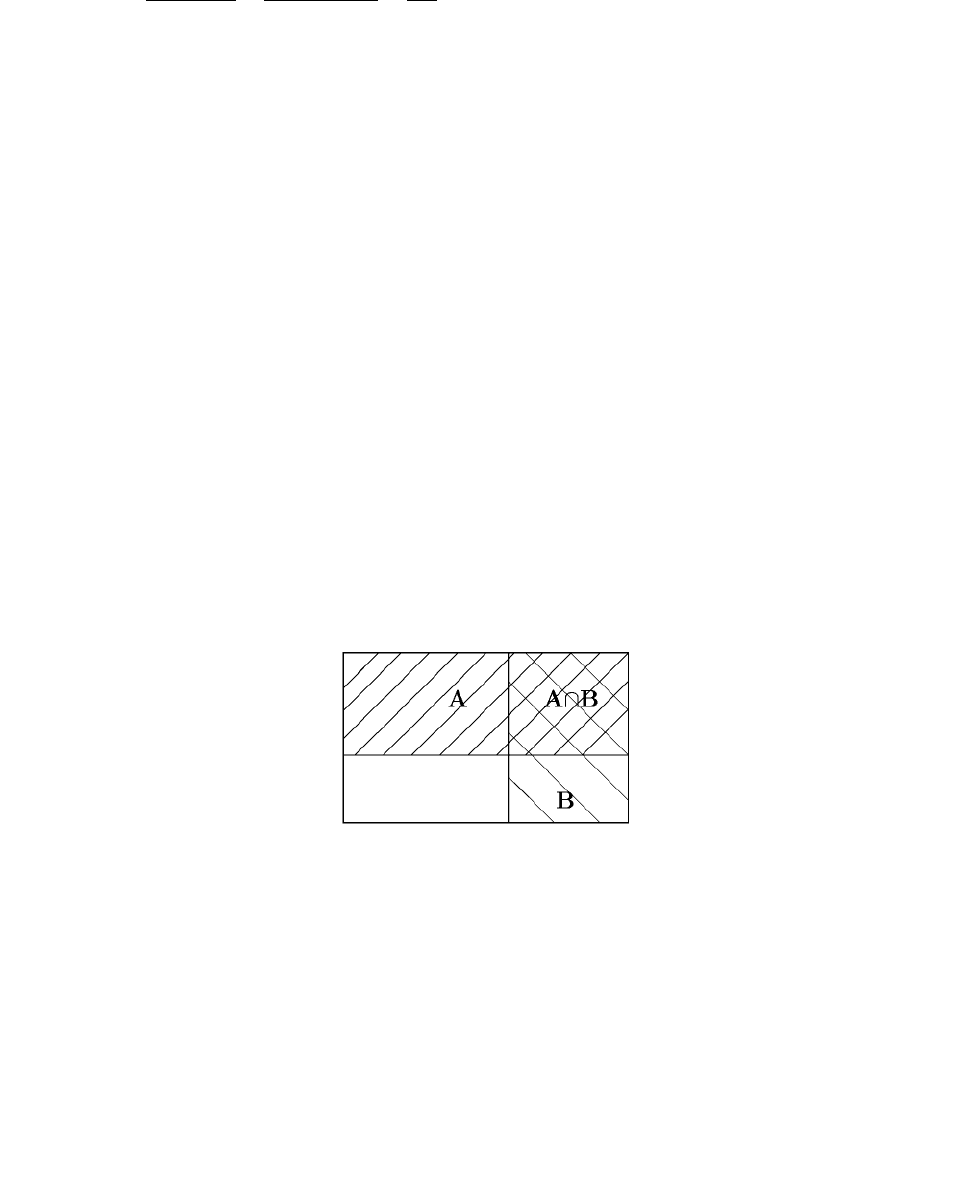
Можно считать, что эксперимент сводится к бросанию точки наудачу в

квадрат. При этом благоприятными исходами (рис. 1.3) являются точки множе-

ства A = {(ξ, η): ⏐ξ − η⏐ ≤ 1/6} (10 минут = 1/6 часа).

То есть попадание во множество A наудачу брошенной в квадрат точки оз-

начает, что X и Y встретятся. Тогда вероятность

встречи равна

)6/5(1

)mes(

)(

−

Ω

AP .

Замечание 1.4. Если даже эксперимент удовлетворяет геометрическому

определению вероятности, далеко не для всех множеств A ⊂ Ω, вероятность

может быть вычислена по формуле (1.3). Причиной этого является существова-

ние так называемых «неизмеримых» множеств, мера которых не существует. А

если не для всех подмножеств Ω мы можем определить их вероятности, следует

сузить класс множеств, называемых

«событиями», оставив в этом классе только

те множества, для которых мы можем определить вероятность.

1.8. Условные вероятности

Нередко мы сталкиваемся с необходимостью оценить «шансы» интере-

сующего нас события A, когда нам известно о том, что произошло некоторое

другое событие B. Для этого вводится понятие условной вероятности.

Пример 1.10. Кубик подбрасывают один раз. Известно, что выпало более

трех очков. Какова при этом вероятность того, что выпало четное число очков?

Рис. 1.4.

Здесь пространство элементарных исходов состоит из трех равновозможных

элементарных исходов: Ω = {4, 5, 6}, и событию A = {выпало четное число оч-

ков} благоприятствуют два из них: А = {4, 6}. Поэтому P(А) = 2/3. Посмотрим

на этот вопрос с точки зрения первоначального эксперимента. Пространство

элементарных исходов при одном подбрасывании кубика состоит из шести то-

чек: Ω = {1, 2, 3, 4, 5, 6}. Слова «известно, что выпало более трех очков» озна-

чают, что в эксперименте произошло событие B = {4, 5, 6}. Слова «какова при

этом вероятность того, что выпало четное число очков?» означают, что нас ин-

тересует, в какой доле случаев при осуществлении B происходит и А. Вероят-

ность события А, вычисленную в предположении, что нечто о результате экс-

перимента уже известно (событие B произошло), обозначим через P(A/B).

Мы хотим вычислить отношение числа исходов, благоприятствующих A

внутри B (то есть благоприятствующих одновременно A и В), к числу исходов,

благоприятствующих B (рис. 1.4)

)(

6/3

6/2

)/(

BAP

∩

===

Определение 1.5. Пусть A и B – два события, причем P(B) > 0. Условной ве-

роятностью события A относительно события B называется вероятность собы-

тия A при условии, что событие B уже произошло, равная

)(

)/(

ABP

BAP =

Если нам известна условная вероятность P(A/B), мы можем вычислить ве-

роятность произведения событий P(AB):

)

()()

()()( B

(1.4)

Формула (1.4) носит название формулы произведения вероятностей. Она

может быть обобщена на случай произвольного числа событий.

Предложение 1.4. (Теорема умножения вероятностей). Пусть A

, … , A

–

события. Тогда справедливо равенство

)/()/()/()()(

12121312121 −

nnn

AAAAPAAAPAAPAPAAAP KKK

. #

Пример 1.11. Студент знает 25 вопросов из 35. Ему наудачу задали три во-

проса. Какова вероятность того, что: а) студент ответит на все три вопроса; б)

хотя бы на два вопроса?

Решение. а) Искомое событие A «студент ответит на все три вопроса» про-

изойдет, если студент ответит правильно на первый вопрос, затем ответит пра-

вильно на второй вопрос и затем ответит правильно на третий вопрос. Отсюда

, где A

321

AAAA ⋅⋅=

– событие «студент ответил правильно на i-й вопрос».

По теореме умножения вероятностей имеем

351,0

333435

232425

235

225

135

125

)/()/()()(

213121

⋅⋅

−

⋅

−

⋅== AAAPAAPAPAP .

Искомое событие C «студент ответит хотя бы на два вопроса» равно

+= , где B – событие «студент ответит ровно на два вопроса». При под-

счете числа благоприятных исходов для события B имеем два независимых

действия – выбор двух вопросов из числа известных (2 из 25) и выбор одного

вопроса из числа неизвестных (1 из 10). Т.к. выборки в данном случае неупоря-

доченные и без повторения, то

по классической формуле (1.2)

458,0

333435

3102425

!35!9!1!23!2

!32!3!10!25

)(

⋅⋅

⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅

⋅

Ω

BP .

Т.к. события A и B – несовместные, то по теореме сложения вероятностей