Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие

Подождите немного. Документ загружается.

)

рица C = {c

} и набор независимых стандартных нормальных случайных вели-

чин

такие, что

,...,(

1 n

ηη=η

111111

nnnnnn

cca

η++η+=ξ

η+

η+=ξ

(4.7)

или в матричной форме:

=ξ Ca .

Предложение 4.8. Случайная величина ξ

в (4.7) имеет нормальное распре-

деление

, где , .#

),(

aN σ

∑

=σ

iji

∑

=ξξ

kjijki

),cov(

Рассмотрим n × n − матрицу B = CC

, где C

− матрица, транспонированная

C. Легко видеть, что такая матрица симметрична (b

= b

) и является невыро-

жденной в силу невырожденности матрицы

C. Более того, из предложения 4.7

следует, что

),cov(

jiij

b ξξ=

Можно также доказать, что матрица

B является строго положительной в

следующем смысле: для любого ненулевого вещественного вектора

0),...,(

≠

zz .

∑∑

jiij

zzb

Матрицу

B = {b

} называют матрицей ковариаций, а вектор −

вектором средних многомерного нормального распределения. Этих двух харак-

теристик достаточно для того, чтобы полностью описать многомерное нор-

мальное распределение. А именно, справедливо следующее утверждение.

()

aaa ,...,

Предложение 4.9. Плотность многомерного нормального распределения

записывается в виде следующей формулы:

⎟

⎠

⎞

⎜

⎝

⎛

−−−

−

ξξ

))(),((

exp

)2(

),,(

2/1

axaxB

xxp

где

),...,(

1 n

xx=x

− определитель матрицы B,

),(

⋅

− обычное евклидово

скалярное произведение в R

∑

vuvu

),(,

),...,(

1 n

uuu

, . #

),...,(

1 n

vvv =

Замечание 4.5. Если n = 1, то функция, выписанная в предложении 4.8,

принимает вид обычной нормальной плотности. Из вида многомерной нор-

мальной плотности видно, что она определяется лишь параметрами

a и B. По-

этому этот закон распределения часто обозначают N(

a, B).

Замечание 4.6. Утверждение предложения 4.8 можно считать эквивалент-

ным определением многомерного нормального распределения. Если плотность

имеет указанный вид с некоторой невырожденной положительной матрицей

то существуют такие a,

C и

, что справедливо представление (4.7).

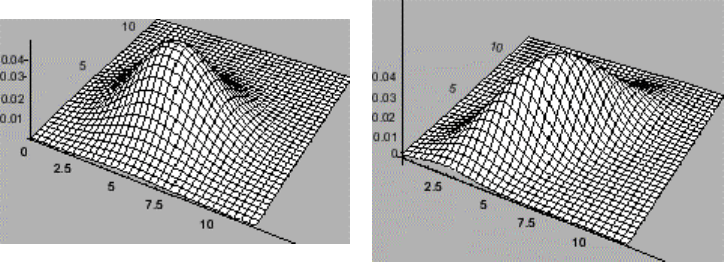
На рис 4.2 приведены примеры двумерных нормальных плотностей.

⎟

⎠

⎞

⎜

⎝

⎛

,)5;5,5(

⎟

⎠

⎞

⎜

⎝

⎛

,)6;5,5(

Рис. 4.2. Примеры двумерных нормальных плотностей.

Предложение 4.10. Предположим, что вектор ),...,(

1 n

имеет много-

мерное нормальное распределение. Тогда любой набор его компонент

имеет (k−мерное) нормальное распределение. #

),...,(

1 k

ξξ=ξ

′

Замечание 4.7. Иногда матрица C, участвующая в соотношениях (4.7),

имеет ранг меньше чем n. В этом случае говорят, что ),...,(

1 n

ξξ=

имеет вы-

рожденное многомерное нормальное распределение. У такого распределения

плотность не существует.

Глава 5. Предельные законы теории вероятностей

Под законом больших чисел в широком смысле понимается принцип, со-

гласно которому, по формулировке А.Н. Колмогорова, совокупное действие

большого числа случайных факторов приводит, при некоторых весьма общих

условиях, к результату, почти не зависящему от случая. Иными словами, при

большом числе случайных величин их средний результат перестает быть слу-

чайным

и может быть предсказан с большой степенью определенности.

Под законом больших чисел в узком смысле понимается ряд математиче-

ских теорем, в каждой из которых для тех или иных условий устанавливается

факт приближения средних характеристик большого числа испытаний к неко-

торым определенным постоянным.

Без преувеличения можно сказать, что закон больших чисел является

од-

ним из наиболее важных утверждений теории вероятностей. В этой главе рас-

смотрим классические теоремы, имеющие универсальный характер – закон

больших чисел и центральную предельную теорему, которые имеют исключи-

тельное значение для математической статистики.

5.1. Закон больших чисел

В § 2.13 был рассмотрен закон больших чисел для случая дискретных слу-

чайных величин. Примечательно то, что он без изменений переносится на об-

щий случай случайных величин.

Предложение 5.1. (Закон Больших Чисел в форме Чебышева). Пусть

− последовательность независимых случайных величин и выполнено

условие

,...,...,

1 n

ξξ

cDNi

≤

∈∀ ][

. Тогда 0>

∀

][][

lim

⎭

⎬

⎫

⎩

⎨

⎧

ε>

ξ++ξ

−

ξ++ξ

∞→

. #

Следствие 5.1. Пусть

,...,...,

1 n

− последовательность независимых оди-

наково распределенных случайных величин с конечной дисперсией:

∞

][

Обозначим aM

ξ ][. Тогда

∀

0lim

⎭

⎬

⎫

⎩

⎨

⎧

ε>−

ξ++ξ

∞→

, или, более кратко,

∞→

→

ξ+

В действительности, это утверждение верно в более общей ситуации,

а именно, предположение о существовании дисперсии не является необходи-

мым. Имеет место так называемый закон больших чисел в форме Хинчина.

Предложение 5.2. (Теорема Хинчина). Пусть

,...,...,

1 n

− последователь-

ность независимых одинаково распределенных случайных величин, у которых

существует математическое ожидание: aM

][. Тогда

∞→

→

ξ++ξ K

. #

5.2. Центральная предельная теорема

Интегральная предельная теорема Муавра-Лапласа, которая рассматрива-

лась в § 2.11, интересна тем, что она является частным случаем общей и уни-

версальной центральной предельной теоремы. Основополагающий вклад в раз-

работку этой тематики внесли выдающиеся отечественные математики:

П.Л. Чебышев, А.А. Марков и А.М. Ляпунов.

Приведем вариант центральной предельной теоремы (ЦПТ)

для независи-

мых одинаково распределенных слагаемых.

Предложение 5.3. (ЦПТ). Пусть

,...,...,

1 n

− последовательность незави-

симых одинаково распределенных случайных величин с конечной дисперсией.

Обозначим aM

ξ ][ и . Тогда

0][

>σ=ξ

∈

∀

)(lim

xFx

⎭

⎬

⎫

⎩

⎨

⎧

≤

−ξ

+ξ

∞→

где

∫

∞−

−

dyexF

)( − функция распределения N(0, 1). #

Замечание 5.1. Обозначим

...

. Тогда , .

Следовательно, утверждение ЦПТ может быть записано в виде

naSM

=][

][ σ= nSD

)(

][

lim

xFx

SMS

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

≤

−

∞→

Как уже отмечалось выше, интегральную теорему Муавра-Лапласа для

схемы Бернулли можно считать следствием ЦПТ.

Замечание 5.2. Существуют обобщения центральной предельной теоремы

на случай независимых разнораспределенных слагаемых. При этом на отдель-

ные слагаемые ξ

накладываются условия, обеспечивающие их «пренебрежимо

малый» вклад в сумму S

с ростом n. Наиболее известными условиями такого

рода являются условия Ляпунова и Линдеберга.

Центральная предельная теорема имеет огромное значение для примене-

ний теории вероятностей в естествознании и технике. Ее действие проявляется

там, где наблюдаемый процесс подвержен влиянию большого числа независи-

мых случайных факторов, каждый из которых лишь ничтожно мало изменяет

течение процесса. Наблюдатель, следящий за состоянием процесса в целом, на-

блюдает лишь суммарное действие этих факторов. Эта схема поясняет также

исключительное место, которое нормальное распределение занимает среди

других вероятностных распределений.

Центральная предельная теорема дает возможность аппроксимировать рас-

пределение сумм независимых случайных величин нормальным распределени-

ем, чем часто пользуются на практике.

В связи с этим, очень важным является

вопрос о том, насколько быстро допредельное выражение в центральной пре-

дельной теореме приближается к F

(x). Приведем формулировку теоремы Бэр-

ри-Эссеена о скорости сходимости в ЦПТ.

Предложение 5.4. (Теорема Бэрри

−

Эссеена). Предположим, что выполне-

ны условия ЦПТ для независимых одинаково распределенных случайных вели-

чин, и, кроме того, существует

][

ξM

. Тогда справедлива оценка

xFx

SMS

][

)(

][

sup

≤−

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

≤

−

где c − некоторое число между

π2/1 и 0,8. #

Глава 6. Цепи Маркова

6.1. Основные понятия теории марковских цепей

Пусть {E

, E

, ... , E

} – множество возможных состояний некоторой физи-

ческой системы. В любой момент времени система может находиться только в

одном состоянии. С течением времени система переходит последовательно из

одного состояния в другое. Каждый такой переход называется шагом процесса.

Для описания эволюции этой системы введем последовательность дис-

кретных случайных величин {ξ

, ξ

, ... , ξ

...}. Индекс n играет роль времени.

Если в момент времени n система находилась в состоянии E

, то мы будем счи-

тать, что ξ

= j. Таким образом, случайные величины являются номерами со-

стояний системы.

Определение 6.1. Последовательность {ξ

, ξ

, ... , ξ

...} образует цепь Мар-

кова, если для любого n и любых k

, k

, ... , k

...

)/(),...,/(

1100

ijPikjP

nnnn

=ξ=ξ=ξ

−−

Для цепей Маркова вероятность в момент времени n попасть в состояние

, если известна вся предыдущая история изучаемого процесса, зависит только

от того, в каком состоянии находился процесс в момент (n – 1). То есть при

фиксированном «настоящем» «будущее» не зависит от «прошлого». Свойство

независимости «будущего» от «прошлого» при фиксированном «настоящем»

называется отсутствием последействия или марковским свойством.

Вероятности },...,2,1{,),/()

(

rjiijPnp

nnij

∈

ξ=

−

называются вероят-

ностями перехода из состояния E

в состояние E

за один шаг.

Определение 6.2. Цепь Маркова называется однородной, если вероятности

перехода p

(n) не зависят от n, т.е. если вероятности перехода не зависят от но-

мера шага, а зависят только от того, из какого состояния и в какое осуществля-

ется переход. Для однородных цепей Маркова вместо p

(n) будем писать p

Вероятности перехода удобно располагать в виде квадратной матрицы

⎥

⎦

⎤

⎢

⎣

⎡

rrrr

ppp

...

............

...

22221

11211

P .

Матрица P называется матрицей вероятностей перехода однородной цепи

Маркова за один шаг. Очевидно, что для всех i:

∑

Вектор

, где )),...,,(

21 r

aaa=a (

iPa

, (i, j = 1, 2, ..., r) называется век-

тором начальных вероятностей.

Замечание 6.1. Свойства однородных цепей Маркова полностью опреде-

ляются вектором начальных вероятностей и матрицей вероятностей перехода.

Пример 6.1. Завод выпускает телевизоры определенного типа. В зависимо-

сти от того, находит ли данный тип телевизора спрос у населения, завод в конце

каждого года может находиться в одном из состояний: состояние 1 – спрос

есть, состояние 2 – спроса нет. Пусть вероятность сохранить состояние 1 в сле-

дующем году с учетом возможного изменения спроса равна 0,8, а

вероятность

изменить состояние 2 с учетом мероприятий по улучшению выпускаемой моде-

ли равна 0,6. Тогда процесс производства на данном заводе можно описать це-

пью Маркова с матрицей переходов

⎥

⎦

⎤

⎢

⎣

⎡

4,06,0

2,08,0

P .

В конкретных случаях для описания эволюции цепи Маркова вместо мат-

рицы P используют граф

, вершинами которого являются состояния цепи, а

стрелка, идущая из состояния E

в состояние E

с числом p

над ней показывает,

что из состояния E

в состояние E

возможен переход с вероятностью p

. В том

случае, когда p

= 0, соответствующая стрелка не проводится. Порядок по-

строения граф рассмотрим на примере.

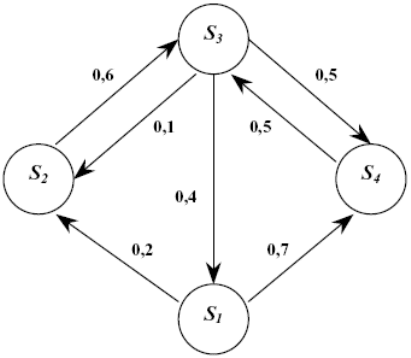
Пример 6.2. По заданной матрице переходов

⎥

⎦

⎤

⎢

⎣

⎡

5,05,000

5,001,04,0

06,04,00

7,002,01,0

построим граф состояний. Имеем (рис. 6.1)

Рис. 6.1.

Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 воз-

можных состояния S

, S

. На графе не отмечаются вероятности перехода

системы из одного состояния в то же самое. При рассмотрении конкретных

систем удобно сначала построить граф состояний, затем определить вероят-

ность переходов системы из одного состояния в то же самое (исходя из требо-

вания равенства единице суммы элементов строк матрицы), а потом составить

матрицу переходов системы.

р ч

Тогда веро-

бы

Предложение 6.1. (Формула Маркова). Пусть – вероятность того, что

в результате n испытаний система перейдет из состояния i в состояние j, l – не-

которое промежуточное состояние между состояниями i и j, п и ем p

)(n

(1) = p

Обозначим соответствующую матрицу переходов как

ijn

= }{

)(

ятность

)(n

p может ть найдена по формуле Маркова

∑

−

ppp

)()()(

, (6.1)

или, что равносильно

. #

mnmn

PPPP ==

−

Замечание 6.2. Равенство (6.1) представляет собой несколько видоизмен-

ную формулу полной вероятности. Зная переходные вероятности (т.е. зная мат-

рицу перехода P = P

), можно найти вероятности перехода из состояния в со-

стояние за два шага

, зная ее – найти матрицу Р

, и т.д.

Пример 6.3. Найти матрицу P

, если известна матрица переходов

⎥

⎦

⎤

⎢

⎣

⎡

7,03,0

9,01,0

Решение.

⎥

⎦

⎤

⎢

⎣

⎡

7,03,0

9,01,0

, ,

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

76,024,0

72,028,0

7,03,0

9,01,0

7,03,0

9,01,0

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

=⋅=

748,0252,0

756,0244,0

76,024,0

72,028,0

7,03,0

9,01,0

213

PPP

6.2. Теорема о предельных вероятностях

Предложение 6.2. (Теорема о предельных вероятностях Биркгофа–

Неймана). Если при некотором n

все элементы матрицы поло-

жительны, то существуют пределы

)]([

jij

bnp

∞→

)(lim , (i, j = 1, 2, ..., r). Предель-

ные вероятности b

не зависят от начального состояния E

и являются единст-

венным решением системы уравнений

⎪

⎩

⎪

⎨

⎧

∑

.,...,2,1,

rjbpb

kjk

(6.2)

Физический смысл этой теоремы заключается в том, что вероятности на-

хождения системы в состоянии E

практически не зависят от того, в каком со-

стоянии она находилась в далеком прошлом.

Цепь Маркова, для которой существуют пределы b

, называется эргодиче-

ской. Решение (b

, b

, ... , b

) системы (6.2) называется стационарным распреде-

лением вероятностей для марковской цепи с матрицей перехода

Если из состояния E

система может перейти в состояние E

с положитель-

ной вероятностью за конечное число шагов, то говорят, что E

достижимо из E

Состояние E

называется существенным, если для каждого состояния E

достижимого из E

, E

достижимо из E

. Если же для хотя бы одного j E

дости-

жимо из E

, а E

не достижимо из E

, то E

– несущественное состояние.

6.3. Области применения цепей Маркова

Цепи Маркова служат хорошим введением в теорию случайных процессов,

т.е. теорию простых последовательностей семейств случайных величин, обыч-

но зависящих от параметра, который в большинстве приложений играет роль

времени. Она предназначена, главным образом, для полного описания как дол-

говременного, так и локального поведения процесса. Приведем некоторые наи-

более изученные в

этом плане вопросы.

Броуновское движение и его обобщения – диффузионные процессы и про-

цессы с независимыми приращениями. Теория случайных процессов способст-

вовала углублению связи между теорией вероятностей, теорией операторов и

теорией дифференциальных уравнений, что, помимо прочего, имело важное

значение для физики и других приложений. К числу приложений относятся

процессы, представляющие интерес для

актуарной (страховой) математики,

теории массового обслуживания, генетики, регулирования дорожного движе-

ния, теории электрических цепей, а также теории учета и накопления товаров.

Мартингалы. Эти процессы сохраняют достаточно свойств цепей Маркова,

чтобы для них оставались в силе важные эргодические теоремы. От цепей Мар-

кова мартингалы отличаются тем, что когда текущее состояние известно,

толь-

ко математическое ожидание будущего, но необязательно само распределение

вероятностей, не зависит от прошлого. Помимо того, что теория мартингалов

представляет собой важный инструмент для исследования, она обогатила но-

выми предельными теоремами теорию случайных процессов, возникающих в

статистике, теории деления атомного ядра, генетике и теории информации.

Стационарные процессы. Эргодическая теорема Биркгофа–Неймана

быть

интерпретирована как результат, описывающий предельное поведение стацио-

нарного случайного процесса. Такой процесс обладает тем свойством, что все

вероятностные законы, которым он удовлетворяет, остаются инвариантными

относительно сдвигов по времени. Эргодическую теорему Биркгофа–Неймана

можно представить как утверждение о том, что при определенных условиях

среднее по ансамблю совпадает со средним по времени. Это означает, что одну

и ту же информацию можно получить из долговременного наблюдения за сис-

темой и из

одновременного (и одномоментного) наблюдения многих независи-

мых копий той же самой системы. Закон больших чисел есть не что иное, как

частный случай эргодической теоремы Биркгофа. Интерполяция и предсказа-

ние поведения стационарных гауссовских процессов, понимаемых в широком

смысле, служат важным обобщением классической теории наименьших квадра-

тов. Теория стационарных процессов – необходимое орудие

исследования во

многих областях.

Марковские процессы (процессы без последействия) играют важную роль

в моделировании систем массового обслуживания (СМО) и социально-

экономических процессов.

РАЗДЕЛ 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Математическая статистика – раздел математики, посвященный ана-

лизу данных. Это самостоятельная область знаний, которая в значительной

степени опирается на понятия теории вероятностей. C формальной точки зре-

ния математическая статистика является такой же формально-логической сис-

темой, как анализ, алгебра и теория вероятностей.

В математической статистике можно выделить два основных направления:

описательную статистику

и индуктивную статистику (статистический вывод).

Описательная статистика занимается накоплением, систематизацией и пред-

ставлением экспериментальных данных в удобной форме. Индуктивная стати-

стика на основе этих данных позволяет сделать определенные выводы относи-

тельно объектов, о которых собраны данные, или оценить их параметры.

Задачи, решаемые математической статистикой, являются, в некотором

смысле, обратными задачам

теории вероятностей. Вероятностные задачи, как

правило, устроены следующим образом: распределения случайных величин

считаются изначально известными, основываясь на знании этих распределений,

требуется найти вероятности различных событий, математические ожидания,

дисперсии, моменты распределений и т.п. В статистических задачах само рас-

пределение считается неизвестным, и целью исследования является получение

более или менее достоверной информации

об этом распределении на основе

данных, собранных в результате наблюдений (экспериментов).

Сравнительная характеристика областей применения теории вероятностей

и математической статистики представлена в следующей таблице:

Области применения теории вероятностей и математической статистики

Теория вероятностей Математическая статистика

1. Модель, описывающая изучае-

мое явление или объект, известна

заранее. Есть сведения обо всей

генеральной совокупности, опи-

сывающей исследуемое явление.

2. Используемый математический

аппарат не зависит от предметной

области.

3. Выводы о поведении исследуе-

мого объекта или явления делают-

ся по всей генеральной совокуп-

ности.

1. Модель, описывающая исследуемое явление, априори

неизвестна.

Для определения модели можно проводить пробные

испытания (сформировать выборку из генеральной со-

вокупности).

3. Иногда модель может быть задана априори с точно-

стью до неизвестных параметров.

4. Значения неизвестных параметров модели могут быть

приближенно получены по выборке из генеральной со-

вокупности.

5. Выводы о поведении объекта или явления делаются

по выборке ограниченного

объема и распространяются

на всю генеральную совокупность.

Отметим, что статистические методы реализованы в различных статисти-

ческих пакетах прикладных программ, например STATISTICA, SPSS,

STATGRAPHICS и др. Задачей данного раздела является освоение основных

понятий и методов математической статистики.