Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие
Подождите немного. Документ загружается.

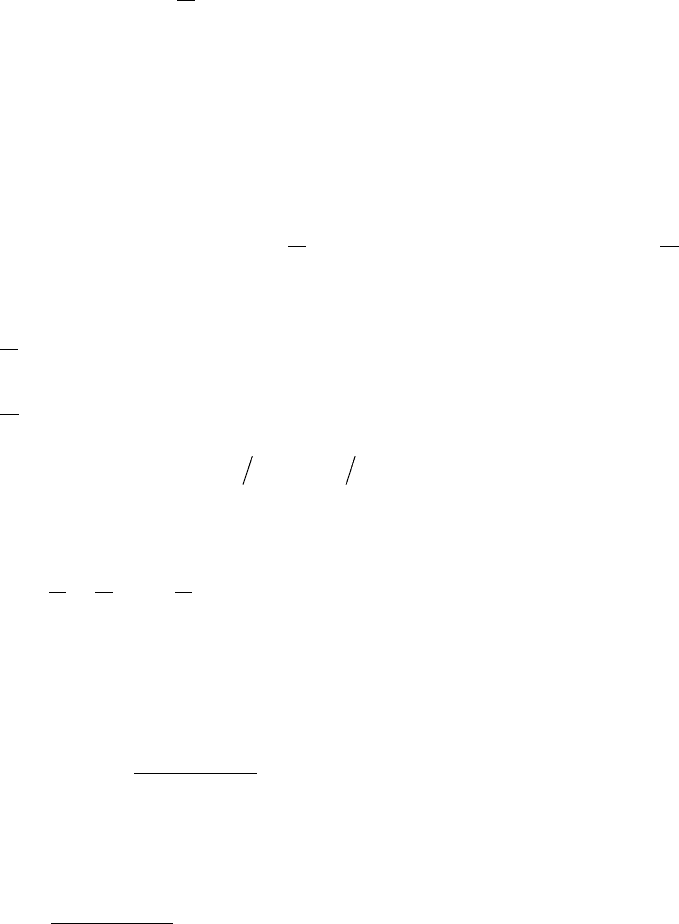
⎪
⎩
⎪
⎨
⎧
>
≤≤−⋅+
−
<
=
ξ
.,1
,,arctg
,,0
)(
ax
axa
a
x
cb
ax
xF
Найти: 1) постоянные b и c; 2) плотность распределения вероятностей p
ξ
(x).
Решение. Для определения b и c воспользуемся свойствами 1) и 2) функции
распределения. Т.к. случайная величина ξ задана на отрезке [−a, a], то должны
выполняться условия:
0)(
=
−aF
и
1)(
=
aF
. В данном случае
0
4
)1arctg()( =
π
−=−⋅+=− cbcbaF
,
1
4
1arctg)( =
π
+=⋅+= cbcbaF
.
В результате получаем систему двух уравнений с неизвестными b и c:
⎪
⎩
⎪
⎨
⎧
=
π
+
=
π
−
,1
4
,0
4
cb
cb
решив которую, найдем
21=b
,
π
=
2c
. Следовательно, случайная величина ξ
характеризуется следующей функцией распределения
⎪
⎩
⎪
⎨
⎧
>
≤≤−
π
+
−
<
=
ξ
.,1
,,arctg
2
2
1
,,0
)(
ax
axa
a
x
ax
xF
Плотность распределения вероятностей определим, используя следствие
3.2. При a
x
−< и a
x
> имеем
0)()(
=
′
=
ξξ
xFxp
. При
],[ aa
x
−
∈
)(
2
)()(
22
xa
a
xFxp
+π
=
′
=
ξξ
.
Итак, случайная величина ξ имеет следующую плотность распределения
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤≤−
+π
−<
=
ξ
.,0
,,
)(
2
,,0
)(
22
ax
axa
xa
a
ax
xp
Пример 3.5. Случайная величина ξ задана плотностью распределения
⎪
⎩
⎪
⎨
⎧
π>
π≤<π
π
≤
=
ξ
.2/,0
,2/4/,2sin2
,4/,0
)(
x
xx
x
xp
Найти функцию распределения F
ξ
(x).
Решение. Если x ≤ π/4, то p
ξ
(x) = 0, следовательно,
∫∫
∞−∞−
ξξ
=⋅==
xx
dtdttpxF 00)()(.
Если π/4 ≤ x ≤ π/2, то
.
∫∫
π
∞−π
ξ
−=+⋅=
4/
4/
2cos2sin20)( xtdtdtxF
x
51

Если x > π/2, то
()
102cos002sin20)(
4/
2/
4/
2/
2/
4/
=+−=⋅++⋅=
∫∫∫
π
∞−
π
π
π
π
π
ξ
xdttdtdtxF
x
.
Итак, случайная величина ξ имеет следующую функцию распределения:
⎪
⎩
⎪
⎨
⎧
π>
π≤<π−
π
≤
=
ξ
.2/,1
,2/4/,2cos
,4/,0
)(
x
xx
x
xF
3.4. Числовые характеристики абсолютно непрерывной случай-
ной величины
Определение 3.8. Математическим ожиданием абсолютно непрерывной
случайной величины ξ с плотностью p
ξ
(x) назовем число
∫
∞
∞−
ξ
=ξ dxxxpM )(][ . (3.3)
По определению, математическое ожидание существует тогда и только то-
гда, когда интеграл (3.3) сходится абсолютно. Формула (3.3) аналогична фор-
муле (2.2) для дискретных случайных величин.
Предложение 3.2. Пусть
RR
g
→:
− некоторая функция. Имеет место
формула:
. Математическое ожидание
∫
∞
∞−
ξ
=ξ dxxpxggM )()()]([
)]([ ξ
g
M
сущест-
вует тогда и только тогда, когда этот интеграл сходится абсолютно. #
В частности,
, а дисперсия равна
∫
∞
∞−
ξ
=ξ dxxpxM )(][
22
[]
∫
∞
∞−
ξ
ξ−=ξ−ξ=ξ dxxpMxMMD )(])[(][][
2
2
, или, учитывая замечание 2.4,
()
2
2
2
2
)()(][][][
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=ξ−ξ=ξ
∫∫
∞
∞−
ξ
∞
∞−
ξ
dxxxpdxxpxMMD . (3.4)
Пример 3.6. Найти математическое ожидание и дисперсию случайной ве-
личины ξ с плотностью распределения
⎪
⎩
⎪
⎨
⎧
∉
∈
=
ξ
.)3,0(,0
,)3,0(,
9
2
)(
x
xx
xp
Решение. Используя формулы (3.3), (3.4), получим
2
39
2
9
2
9
2
)(][
3
0
3
3
0
2
3
0
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
==⋅==ξ
∫∫∫
∞
∞−
ξ
x
dxxxdxxdxxxpM
;
52
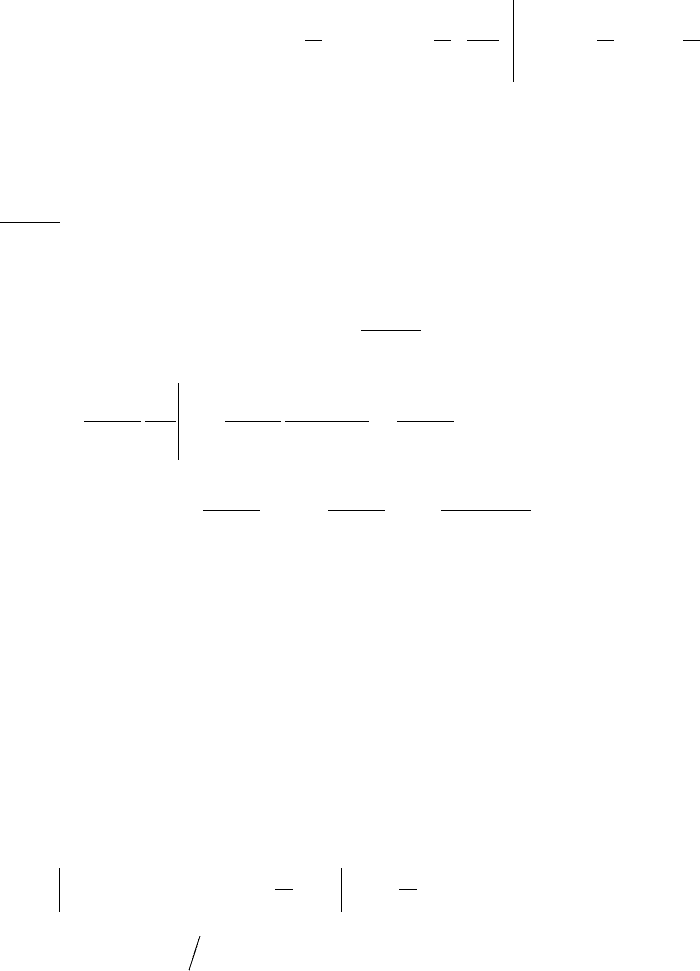
()
2
1
4
2
9
4
49
2
4
9
2
][)(][
3
0
4
3
0
2
2
2
=−=−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=−⋅=ξ−=ξ
∫∫
∞
∞−
ξ
x
xdxxMdxxpxD
.
Пример 3.7. Найдем математическое ожидание и дисперсию равномерного
распределения с плотностью
⎪
⎩
⎪
⎨
⎧
∉
∈
−
=
ξ
.],[,0
,],[,
1
)(
dcx
dcx
cd
xp
Решение. М[ξ] =
∫∫∫∫
+∞
∞−
+∞
∞−
+
−
+=
d
cd
c
dxdx
cd
xdxdxxxf 0
1
0)(
=
=
=
−
d
c
x
cd 2
1
2
22
1
22
dccd
cd
+
=
−
−
.
D[ξ] = M[ξ
2
] − M[ξ]
2
=
12
)(
2
1
2
2
2
cddc
dx
cd
x
d
c
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
∫
.
Пример 3.8. Найдем математическое ожидание и дисперсию показательно-
го распределения с плотностью
⎩
⎨
⎧
≥λ
<
=
λ−
ξ
.0,
,0,0
)(
xe
x
xp
x
Решение.
М[ξ] =
[ u = x, du = dx, dv = , v = = − ] =
=λ
∫
+∞
λ−
0
dxex
x
dxe
xλ−
λ
∫
λ−
λ dxe
x
x
e
λ−
=
+−
+∞
λ−
0
x
xe =
∫
+∞
λ−
0
dxe
x
λ
=
λ
−
∞+
λ−
11
0
0
x
e .
Аналогично находим
2
1][ λ=ξD .
Можно показать, что для случайной величины
ξ, распределенной по нор-
мальному закону
,
),(
2
σaN a
M
=
ξ
][, .
2
][ σ=ξD
Математическое ожидание и дисперсия являются важнейшими числовыми
характеристиками случайных величин. Однако они хотя и являются самыми
важными, но далеко не исчерпывают всего набора употребимых числовых ха-
рактеристик случайной величины. Рассмотрим некоторые из них.
Предположим, что
строго возрастающая функция F(t) есть функция рас-
пределения некоторой
непрерывной случайной величины ξ (рис. 3.3). В даль-
нейшем
α − число между 0 и 1.
Определение 3.9. Квантилью уровня α для распределения, порождаемого
функцией
F
ξ
(t), называется число k
α
, являющееся решением уравнения
α=
<
ξ=
ααξ
}{)( kPkF ,
53
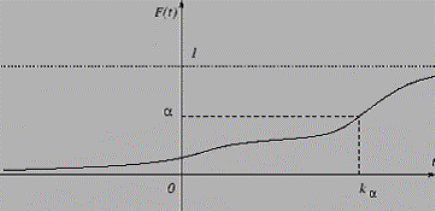
т.е. , где − функция, обратная к функции F. )(
1
α=
−
α
Fk RF →
−
)1,0(:
1
Рис. 3.3.
Замечание 3.4. Квантили часто называют также процентными точками
распределения. Под 100
α%−ной точкой k
100α%
подразумевается квантиль k
1–α
,
т.е. такое значение случайной величины
ξ, при котором . α=≥ξ
α−
}{
1
kP
Квантиль k
0,5
случайной величины ξ называется медианой Me[ξ]. Она ис-
пользуется в качестве показателя центра группирования наряду с математиче-
ским ожиданием. Для абсолютно непрерывных случайных величин медиана –
это граница, левее и правее которой находятся значения случайной величины с
вероятностями, равными 0,5.
Для дискретных случайных величин медиана находится на отрезке, кото-
рый определяется из условий:
.
5,0,5,0
1
11
>≤
∑∑
+
==
l
i
i
l
i
i
pp
Чаще всего пользуются, кроме медианы
k
0,5
, квантилями k
0,25
и k
0,75
, кото-
рые называются
квартилями.
Предложение 3.3. Предположим, что ξ − абсолютно непрерывная случай-
ная величина с четной плотностью
p(x), то есть
)()(
x
p
x
pR
x
−=
∈
∀
. Тогда
1) 1)()(
=−+∈∀
t
F
t
F
R
t
,
2)
α−α
−
=∈α∀
1
)1,0( kk
.
Доказательство. Для определенности считаем, что t ≥ 0. Производя замену
переменных в интеграле и пользуясь четностью плотности, получим цепочку
равенств
==−≤ξ=−
∫
−
∞−
t
dxxptPtF )(}{)([замена x =
−
z] ==−=
∫∫
+∞+∞
tt
dzzpdzzp )()(
)(1}{1}{
t
F
t
P
t
P
−
=
≤
ξ
−
=
≥ξ=
.
Первая часть предложения доказана, вторая вытекает из первой.
Если функция распределения
F(t) удовлетворяет тождеству
1)()(
=
−
+
t
F
t
F
,
то соответствующее ей распределение называется
симметричным.
Для абсолютно непрерывных распределений в качестве числовой характе-
ристики используют
моду. Модой называется точка локального максимума
54

функции плотности. Мода случайной величины ξ обозначается Mo[ξ]. Распре-
деления, имеющие одну моду, называются унимодальными, несколько – поли-
модальными.
Замечание 3.5. Для нормального распределения Me[ξ] = Mo[ξ] = M[ξ].
Определение 3.10. Начальным моментом k−го порядка случайной величи-
ны
ξ называется математическое ожидание k−й степени этой величины
][][
k
kk
M ξ=ν=ξν .
Определение 3.11. Центральным моментом k−го порядка случайной вели-
чины
ξ называется математическое ожидание k−й степени отклонения величи-
ны
ξ от ее математического ожидания
]])[[(][
k
kk
MM ξ−ξ=µ=ξµ .
Формулы для вычисления моментов для дискретных случайных величин
(принимающих значения
x
i
с вероятностями p
i
) и непрерывных (с плотностью
вероятности
p
ξ
(x)) приведены в таблице 3.1.
Таблица 3.1.
Нетрудно заметить, что при k = 1 первый начальный момент случайной ве-
личины
ξ есть ее математическое ожидание, т.е.
][
1
ξ
=
ν
M
, а при k = 2 второй
центральный момент – дисперсия, т.е.
][
2
ξ
=
µ
D
.
При изучении распределений, отличных от нормального, возникает необ-
ходимость количественно оценить это различие. С этой целью вводят специ-
альные характеристики, в частности
асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному. Наоборот, боль-
шие значения асимметрии и эксцесса указывают на значительное отклонение от
нормального.
Определение 3.12. Коэффициентом асимметрии теоретического распре-
деления называют отношение центрального момента третьего порядка к кубу
среднего квадратического отклонения:
3
3
σµ=β .
55
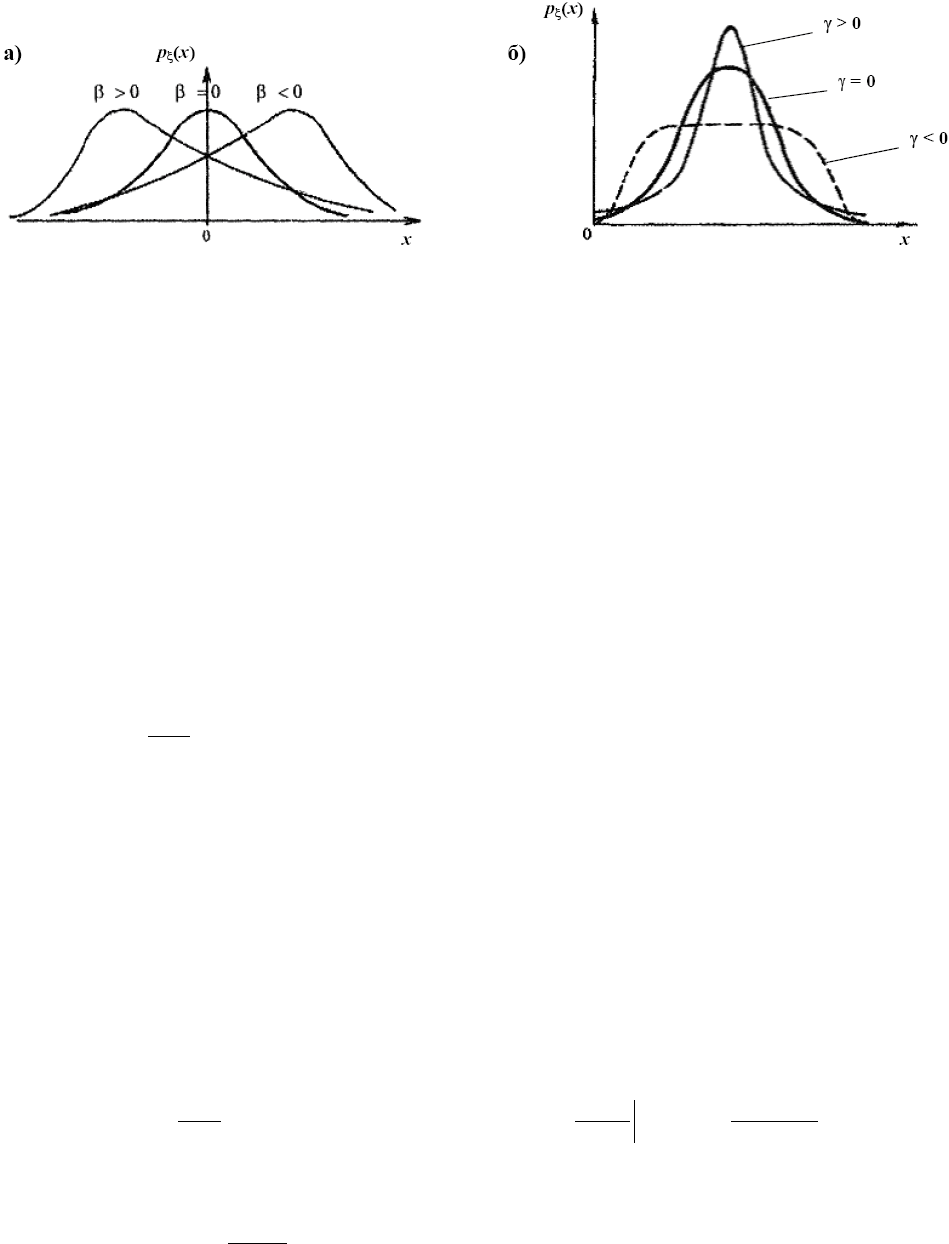
Для симметричного распределения β (и µ
3
) равен нулю. При β < 0 распре-
деление имеет левостороннюю асимметрию (средняя арифметическая меньше
медианы), при
β > 0 − правостороннюю (рис. 3.4,а).
Рис. 3.4. Зависимость формы плотности распределения вероятности от: а) ко-
эффициента асимметрии; б) коэффициента эксцесса.
Определение 3.13. Коэффициентом эксцесса теоретического распределе-
ния называют характеристику, которая определяется равенством
.
3/
4
4
−σµ=γ
Распределение с более острой вершиной – с крутизной, большей, чем у
нормального распределения, имеет
γ > 0; распределение, более плоское, чем
нормальное, имеет γ < 0. Зависимость формы плотности распределения от γ
приведена на рис. 3.4,б.
Пример 3.9. Случайная величина ξ – годовой доход (в усл. ед.) наугад взя-
того лица, облагаемого налогом. Ее плотность распределения имеет вид
p
ξ
(x) =
⎪
⎩
⎪
⎨
⎧
<
≥
,5,0
,5,
1,3
x
x
x
a
где
a – неизвестный параметр.
Требуется: а) определить значение параметра
a; б) найти функцию распре-
деления
F
ξ
(x); в) определить математическое ожидание и среднее квадратиче-
ское отклонение; г) определить размер годового дохода
x
l
, не ниже которого с
вероятностью
P = 0,5 окажется годовой доход случайно выбранного налогопла-
тельщика.
Решение. Воспользуемся условием нормировки: . 1)( =
∫
+∞
∞−
ξ
dxxp
10
5
5
1,3
=+
∫∫
∞−
+∞
dx
x
a
dx , откуда =
∫
+∞
−
5
1,3
dxxa +=
−
∞+
−
0
1,2
5
1,2
x
a
1
51,2
1,2
=
⋅
a
,
следовательно,
.
667,611,25
1,2
=⋅=a
Итак,
⎪
⎩
⎪
⎨
⎧
<
≥
=
ξ
.7,0
,7,
1,324
)(
5,3
x
x
x
xp
56
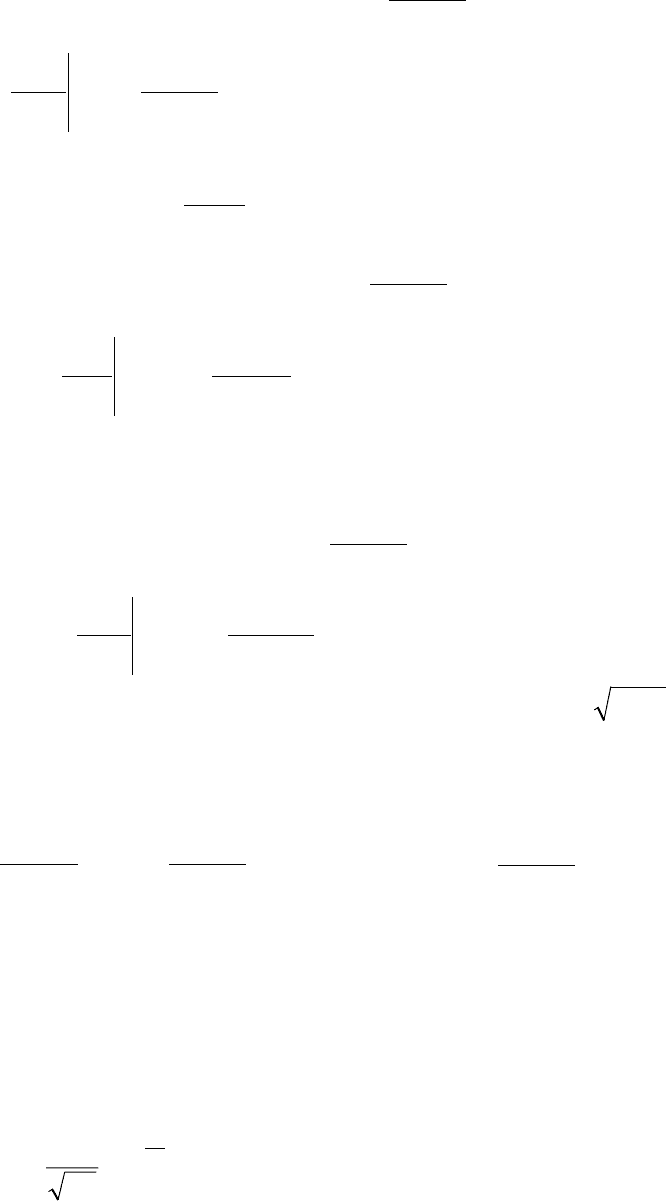
Функция распределения
∫
∞−
ξξ
=
x
dxxpxF )()(.
Для
x < 5: F
ξ
(x) = 0, т.к. при x < 5 p
ξ
(x) = 0.
Для
x ≥ 5: ==
∫
∞−
ξξ
x
dxxpxF )()(
∫∫
∞−
+
5
5
1,3
667,61
0
x
dx
x
dx
==
∫
−
x
dxx
5
1,3
667,61
=
x
x
5
1,2
1,2
667,61
−
−
=
5,2
64,129
1
x
− .
Итак,
⎪
⎩
⎪
⎨
⎧
≥−
<
=
ξ
.5,
5,129
1
,5,0
)(
1,2
x
x
x
xF
==ξ
∫
+∞
∞−
ξ
dxxxpM )(][ +⋅
∫
∞−
5
0 dxx 667,61
667,61
7
1,3
=
∫
+∞
dx
x
x =
∫
+∞
−
7
1,2
dxx
=
+∞
−
−
5
1,1
1,1
667,61
x
545,9
51,1
667,61
0
1,1
≈
⋅
+= .
2222
][)(][][][ ξ−=ξ−ξ=ξ
∫
+∞
∞−
ξ
MdxxpxMMD
,
=
∫
+∞
∞−
ξ
dxxpx )(
2
∫
∞−
+⋅
5
2
0 dxx
667,61
667,61
5
1,3
2
=
∫
+∞
dx
x
x
=
∫
+∞
−
7
1,1
dxx
+∞
−
−
⋅=
5
1,0
1,0
667,61
x
525
51,0
667,61
0
1,0
≈
⋅
+= . Следовательно,
D[ξ] = M[ξ
2
] − M[ξ]
2
≈ 525 − (9,545)
2
≈ 433,884; σ
ξ
= ][ξD ≈ 20,83.
Т.к. по определению
F
ξ
(x) = P(ξ < x) и P(ξ < x) + P(ξ ≥ x) = 1, то
P(ξ ≥ x) = 1 − P(ξ < x) = 1 − F
ξ
(x),
следовательно,
P(ξ ≥ x
1
) = 1 − F
ξ
(x
1
) = 0,5, откуда F
ξ
(x
1
) = 0,5.
5,0
667,61
1
1,2
1
=−
x
; ;5,05,01
667,61
1,2
1
=−=
x
335,123
5,0
667,61
1,2
1
≈=x
.
Отсюда
.
894,9335,123335,123
476,01,2/1
1
≈==x
3.5. Нормальное распределение
Функция распределения стандартного нормального закона
N(0, 1), ввиду ее
важности имеет специальное обозначение:
∫
∞−
−
π
=
t
x
dxetF
2
0
2
2
1
)(
&
. (3.5)
Ее график (см. рис. 3.5) называют
нормальной кривой (кривой Гаусса). Плот-
ность стандартного нормального закона обозначают как
ϕ(x).
57
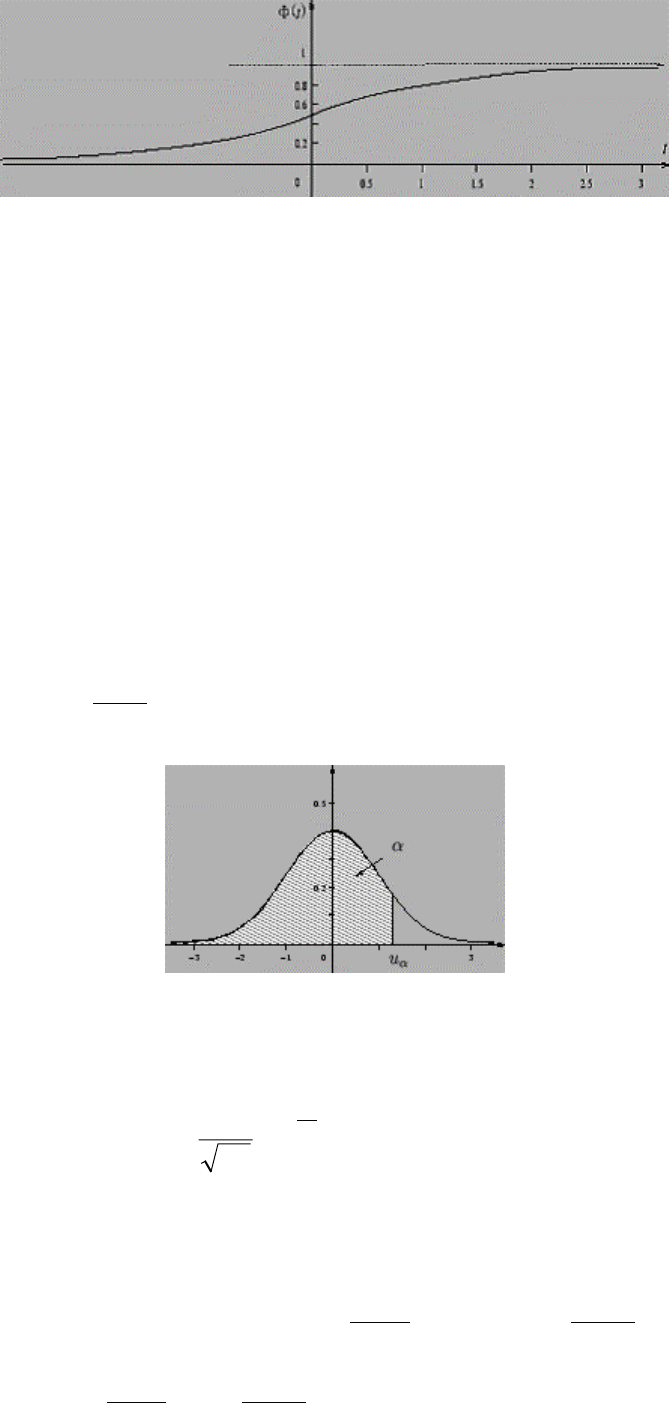
Рис. 3.5.
Квантили этого распределения (рис. 3.6) будем обозначать как
α
=
αα
)(:
0
uFu .
Функция
F
0
(t) не является элементарной, то есть, интеграл в (3.5) не может
быть сведен к табличным и быть композицией элементарных функций. Для
функции
F
0
(t) составлены подробные таблицы, ее значения вычисляются мно-
гими прикладными программами. С их помощью, например, можно найти, что
399865,0)3(
99865,00
≈
⇒≈ uF . (3.6)
Согласно
предложению 3.3 имеем тождества
1)()(
00
=
−+ tFtF
,
αα−
−
= uu
1
. (3.7)
Если
ξ имеет распределение , то ),(
2
σaN
σ
−
ξ
/)( a
− стандартная нормальная
случайная величина. Функция распределения случайной величины
ξ легко за-
писывается через функцию
F
0
(t):
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
=
σ
at
FtF
aN
0
),(
)(
2
.
Рис. 3.6.
Замечание 3.6. Т.к.
5,0)0(
0
=
F
, то F
0
(t) можно выразить через функцию
Лапласа
Φ(t), равную
∫
−
π
=Φ
t
x
dxet
0
2
2
2
1
)(
. А именно, . )(5,0)(
0
ttF Φ+=
Найдем вероятность попадания в интервал для случайной величины
ξ с
распределением
N(a, σ
2
):
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
−α
Φ+−
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
−β
Φ+=α−β=β<ξ<α
aa
FFP 5,05,0)()()(
⎟
⎠
⎞
⎜
⎝
⎛
σ
−α
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
σ
−β
Φ=
aa
.
58
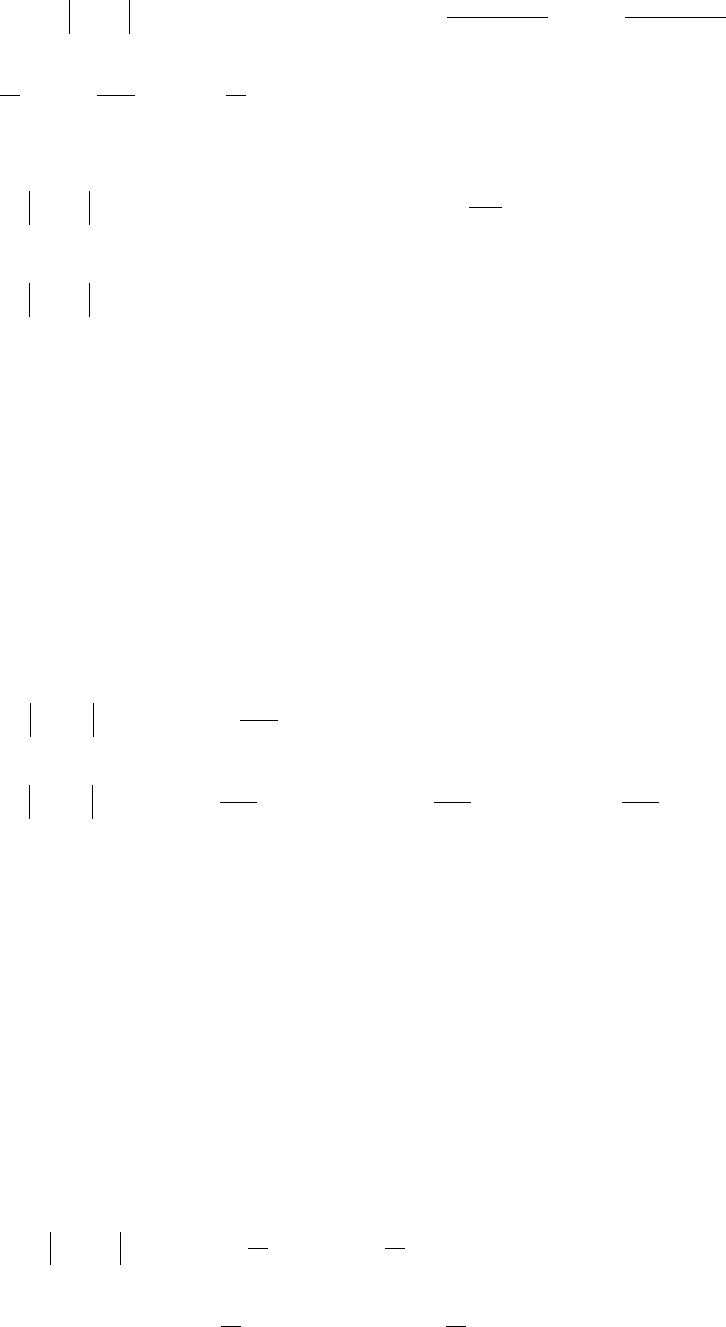
Откуда
{}
=
⎟
⎠
⎞
⎜
⎝
⎛
σ
−δ−
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
σ
−δ+
Φ=δ+<δ−=δ<−ξ
aaaa
aaPaP
)(
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ=
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ−
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ=
2.
Положив в последней формуле
δ = 3σ, получим
{}
9973,049865,02)3(2
3
2)33(3 =⋅≈Φ=
⎟
⎠
⎞
⎜
⎝
⎛
σ
σ
Φ=σ+<σ−=σ<−ξ aaPaP
.
Следовательно,
{
}
0027,09973,013
=
−
≈
σ>−ξ aP . (3.8)
Вероятность в правой части, пренебрежимо мала для многих практических
применений. Поэтому правило «трех сигм» читают так:
нормальная случайная
величина уклоняется от своего среднего не более чем на три корня из диспер-
сии
. Как видно из (3.8), это правило ошибочно лишь в 0,27% случаев.
Пример 3.10. На станке изготовляются втулки, длина которых L представ-
ляет нормально распределенную случайную величину, причем
М[L] = 20cм,
σ = 0,2 см. Найти: 1) вероятность того, что длина втулки будет отклоняться от
ее среднего значения на величину, меньшую 0,3 см; 2) длину втулки с вероят-
ностью 0,95; 3) длину втулки с вероятностью 0,9973.
Решение. По условию a = 20см, σ = 0,2 см.
{}
8662,04332,02)5,1(2
2,0
3,0
23,0
=⋅≈Φ=
⎟
⎠
⎞
⎜
⎝
⎛
Φ=<− aLP
.
{}
⇒=
⎟
⎠
⎞
⎜
⎝
⎛
δ
Φ⇒=
⎟
⎠
⎞
⎜
⎝
⎛
δ
Φ=δ<−
475,0
2,0
95,0
2,0
2aLP
⇒=
δ
96,1
2,0
⇒=δ⇒ 392,0 20 – 0,392 < L < 20 + 0,392 ⇒ 16,608 < L < 20,392.
Пример 3.11. Фирма занимается выпуском фломастеров. Станок−автомат
контролирует их диаметры
Х, пропуская в упаковки фломастеры с диаметром
10 мм, допуская отклонение от стандарта 0,1 мм. В выпущенной партии было
забраковано автоматом 0,27% фломастеров. Найти интервал, в котором заклю-
чены диаметры выпущенных фломастеров.
Решение. Известно, что средний размер диаметра фломастеров, т.е.
M[Х] = а = 10, среднее квадратическое отклонение σ = 0,1. Вероятность выпус-
ка не бракованных фломастеров составляет 99,73%, т.е. 0,9973.
Воспользуемся формулой:
{}
9973,022 =
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ⇒
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ=δ<− aXP
.
Отсюда найдем
δ: 4987,09973,02 =
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ⇒=
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ
.
По таблице значений функции Лапласа находим, что
δ/σ = 3, отсюда сле-
дует,
δ = 3σ; δ = 3⋅0,1 = 0,3, δ = 0,3.
59

Найдем искомый интервал из неравенства:
3,010 <−X ⇒ –0,3 < X – 10 < 0,3 ⇒ 10 – 0,3 < X < 10 + 0,3 ⇒ 9,7 < X < 10,3.
Получили интервал (9,7; 10,3), в котором с вероятностью 0,9973 будут за-
ключены диаметры изготовленных фломастеров.
Глава 4. Совместное распределение случайных величин
Задачи, в которых участвует только одна случайная величина, редки. Как
правило, результат опыта определяется несколькими случайными величинами
(
ξ
1
, … , ξ
n
), образующими случайный вектор или многомерную случайную вели-
чину
. Формализм для изучения распределений случайных векторов вполне ана-
логичен рассмотрению распределения одной (скалярной) случайной величины.
4.1. Совместная функция и плотность распределения
Как и раньше, наиболее универсальным инструментом являются функции
распределения.
Определение 4.1. Совместной функцией распределения случайных величин
ξ
1
, … , ξ
n
назовем функцию ), зависящую от n вещественных пе-
ременных, такую, что
,...,(
1...
1
n
xxF
n
ξξ
{
}
nnn
xxPxxF
n
≤
ξ
≤
ξ
=
ξξ
,...,),...,(
111...
1
.
Предложение 4.1. Перечислим некоторые свойства функций распределе-
ния нескольких случайных величин:
1.
.
1),...,(0
1...
1
≤≤
ξξ n
xxF
n
2. Монотонность по каждой переменной, например,
),...,,(),...,,(
2
)2(
1...2
)1(
1...
)2(
1
)1(
1
11
nn
xxxFxxxFxx
nn
ξξξξ
≤<∀
.
3. Пределы на «минус бесконечности». Если в совместной функции распреде-
ления зафиксировать все переменные, кроме одной, а оставшуюся переменную
устремить к
−∝, то этот предел равен нулю. Например, для фиксированных
n
xxx ,...,,
31
0),...,,,(lim
321...
1
2
=
ξξ
−∞→
n
x
xxxxF
n
.
4. Пределы на «+
∝ или –∝ бесконечности»:
1),...,(lim
1...
...
1
1
=
ξξ
+∞→
+∞→
n
x
x
xxF
n
n
,
0),...,(lim
1...
...
1
1
=
ξξ
−∞→
−∞→
n
x
x
xxF
n
n
.
5. Если зафиксируем все переменные, кроме одной, которую устремим к +
∝,
получим функцию распределения меньшего набора случайных величин. На-
пример,
),,...,(),...,(
11...11...
111
+
∞=
−ξξ−ξξ
−
nn
xxFxxF
nn
. #
Наиболее удобный для теории и очень важный для практических приложе-
ний случай – это случай абсолютно непрерывных распределений.
60
