Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие
Подождите немного. Документ загружается.

ходов (т.е. исходов, для которых {X
i
< x}) к общему числу исходов n, а при пе-
реходе к случайной выборке
X
1
, … , X
n
становится случайной величиной µ(x)/n,
где µ(x) – биномиальная случайная величина.
Согласно теореме Бернулли (см.
следствие 2.2), частость µ(x)/n сходится
по вероятности к вероятности
p, поэтому
)(}{
)(
)( xFxPp
n
x
xF
P
n
n
ξ
→∞
=<ξ=→
µ
= .
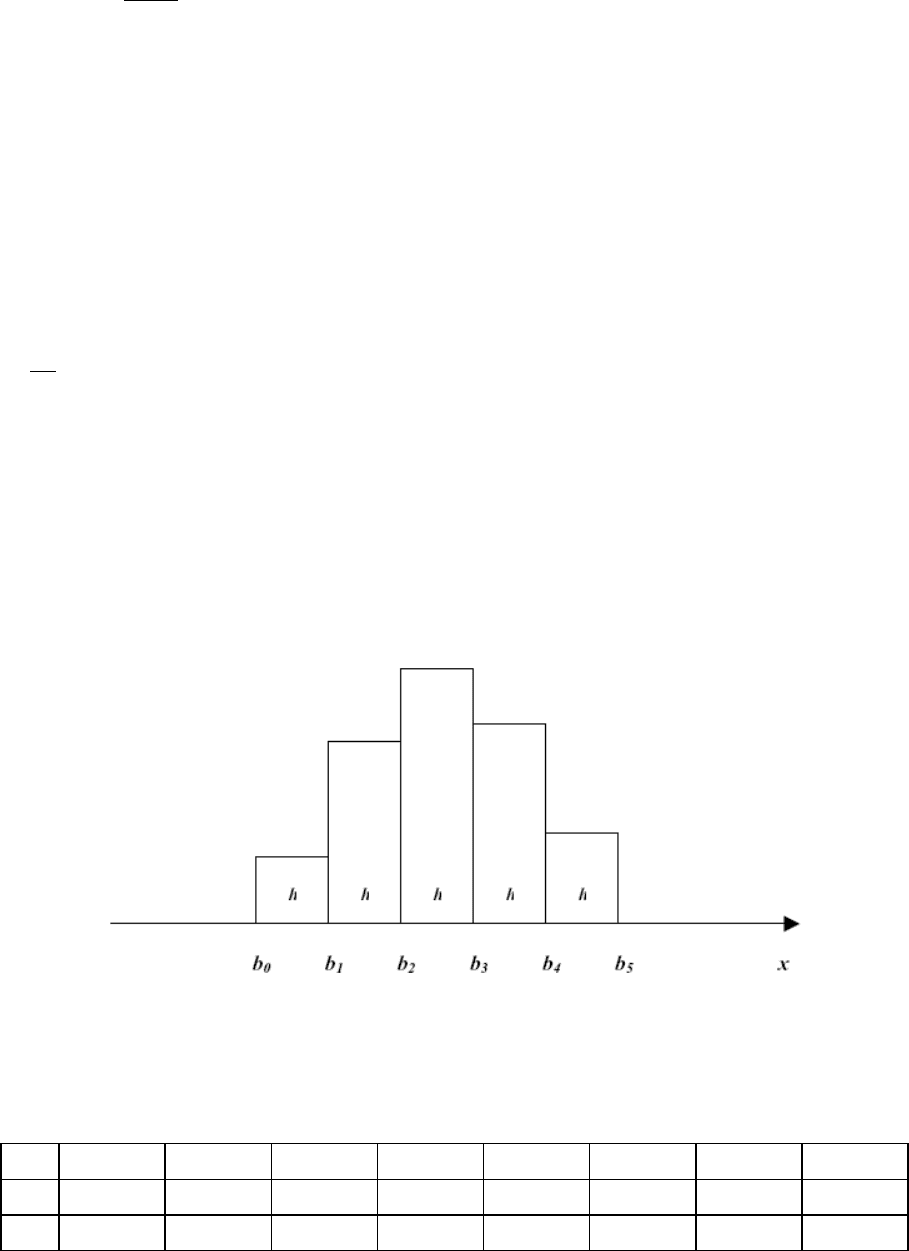
Функция плотности p
ξ
(x) оценивается с помощью гистрограммы следую-
щим образом. Вся числовая прямая разбивается на
L непересекающихся полу-
интервалов
∞
=
−
∞
=
==
− Liii
bbLibbh ,,,...,1),,[
01
, по конкретной выборке
x
1
, … , x
n
подсчитывается число наблюдений n
i
, i = 1,…, L, попавших в каждый
интервал. Затем над каждым полуинтервалом
i-м строится прямоугольник,
площадь которого пропорциональна
n
i
.
Точно так же, как и выше, можно доказать, что частости попадания на по-
луинтервалы сходятся по вероятности к соответствующим вероятностям
{}
ii
b
b
P
n
i
bxbPdxxp
n
n
i
i
<≤=→
−ξ
∞→
∫
−
1
1
)(
.
При подходящем подборе полуинтервалов гистограмма
p
n
(x) будет напо-
минать график функции плотности
p
ξ
(x).
Если известно, что плотность отлична от нуля только на некотором отрез-
ке, то полуинтервалы можно, и желательно, выбирать одинаковой длины
h, а
площади прямоугольников – равными частостям
n
i
/n. Поэтому вся площадь под
гистограммой будет равна единице. На рис. 7.2 показан пример такой гисто-
граммы.
Рис. 7.2.
Пример 7.2. Выборочная проверка размеров дневной выручки оптовой ба-
зы от реализации товаров по 100 рабочим дням дала следующие результаты:
i
1 2 3 4 5 6 7 8
J
i
0 – 5 5 – 10 10 – 15 15 – 20 20 – 25 25 – 30 30 – 35 35 – 40
n
i
2 7 14 19 25 20 10 3
91
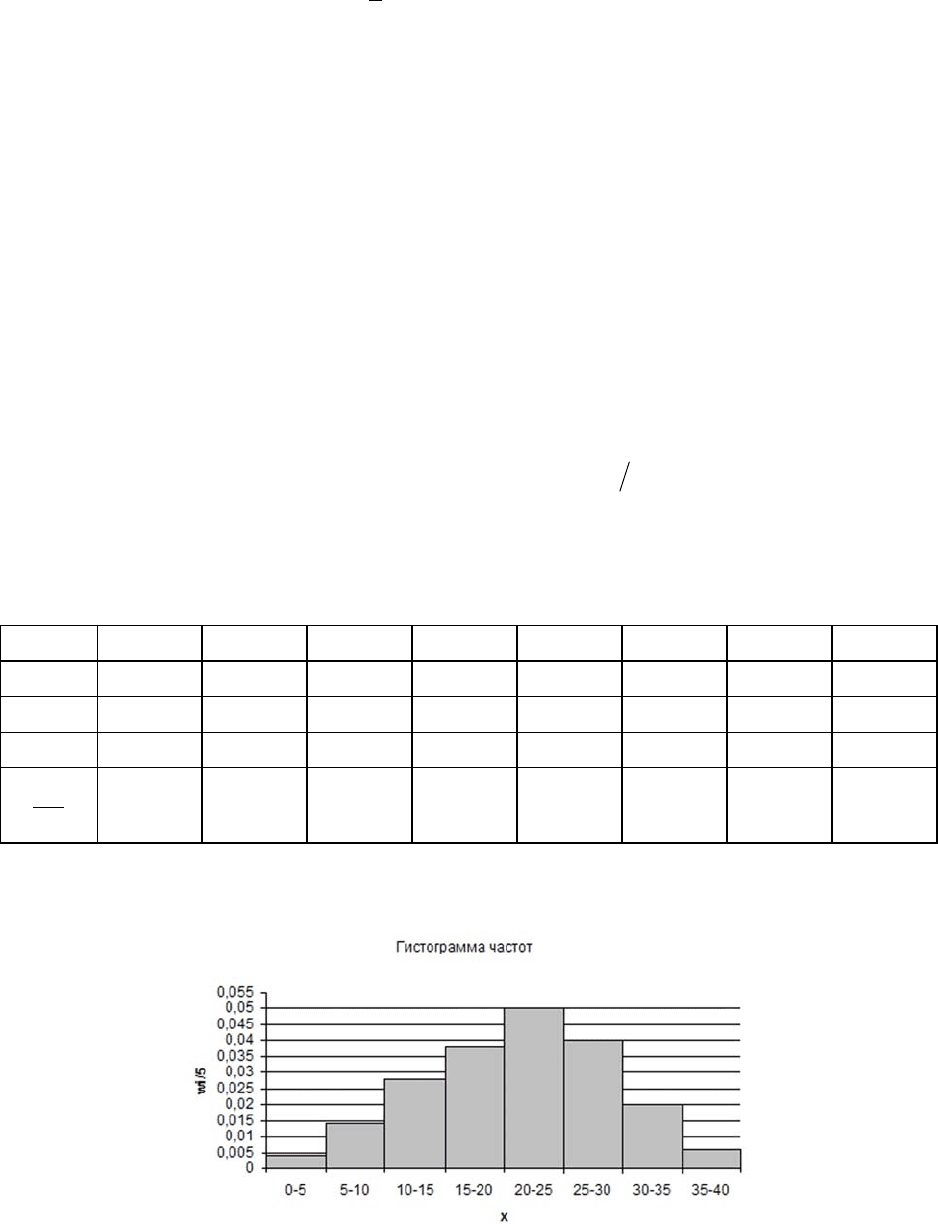
Здесь, i – номер интервала значений дневной выручки (i = 1, … , 8); J
i
– грани-
цы
i-того интервала (в условных денежных единицах); n
i
– число рабочих дней,
когда дневная выручка оказывалась в пределах
i-го интервала; при этом оче-
видно, что
. Требуется:
100
8
1
==
∑
=
nn
i
i
1) построить гистограмму частот;
2) найти несмещенные оценки
x
и s
2
для математического ожидания и диспер-
сии случайной величины Х (дневной выручки оптовой базы) соответственно;
3) определить приближенно вероятность того, что в наудачу выбранный рабо-
чий день дневная выручка составит не менее 15 условных денежных единиц.
Решение.
1) В условиях данной задачи естественно исходить из того, что наблюдае-
мая случайная величина
Х (дневная выручка оптовой базы) имеет непрерывное
распределение вероятностей.
Статистическим аналогом графика плотности распределения такой случай-
ной величины, как известно, является гистограмма относительных частот. Она
представляет собой совокупность прямоугольников, построенных на выделен-
ных интервалах наблюденных значений случайной величины
Х как на основа-
ниях. Площадь каждого
i-го прямоугольника равна относительной частоте w
i
i-
го интервала, определяемой по формуле
nnw
ii
/
=
, так что 1.Отсюда
высота
i-го прямоугольника вычисляется ка
8
1
=
∑
=i
i
w
к
i
h где h
i
w
).
i
– величина i-го
интервала (в данной задаче
h
i
= h = 5 для всех i = 1, … , 8
Полная площадь гистограммы, таким образом, равна единице. На основе
изложенного для построения гистограммы составим следующую таблицу.
i 1 2 3 4 5 6 7 8
J
i
0 – 5 5 – 10 10 – 15 15 – 20 20 – 25 25 – 30 30 – 35 35 – 40
n
i
2 7 14 19 25 20 10 3
w
i
0,02 0,07 0,14 0,19 0,25 0,20 0,10 0,03
5
i
w
0,004 0,014 0,028 0,038 0,05 0,04 0,02 0,006
Построим гистограмму:
92
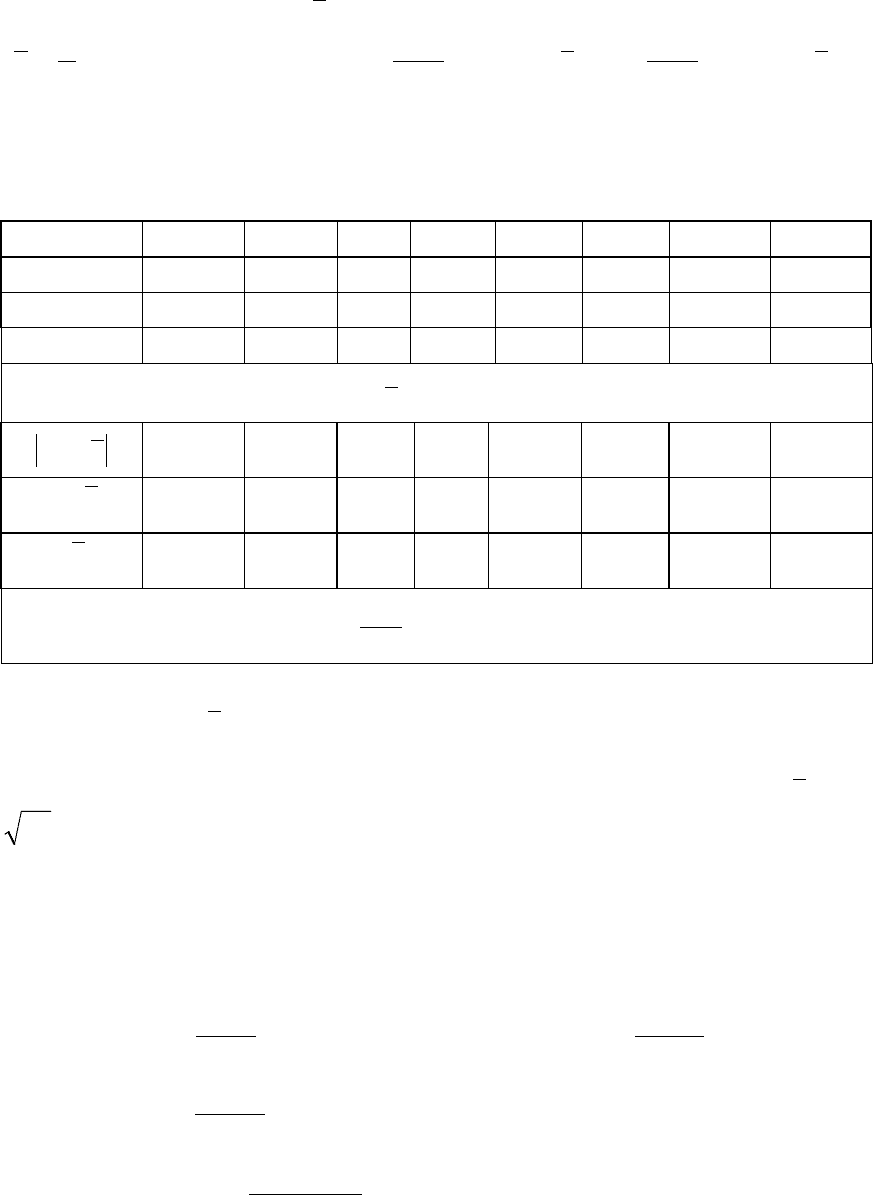
Вид этой гистограммы позволяет считать рассматриваемое распределение
вероятностей нормальным.
2) Несмещенные оценки
x
и s
2
найдем по формулам
∑∑
==
==
8
1
8
1
1
i
ii
i
ii
wxnx
n
x ,
∑∑
==
−
−
=−
−
=
8
1
2
8
1
22
)(
1
)(
1
1
i
ii
i
ii
wxx
n
n
nxx
n
s
,
где
x
i
– середина i-го интервала.
Все необходимые вычисления для удобства и наглядности проведем в рам-
ках следующей таблицы:
i
1 2 3 4 5 6 7 8
x
i
2,5 7,5 12,5 17,5 22,5 27,5 32,5 37,5
w
i
0,02 0,07 0,14 0,19 0,25 0,20 0,10 0,03
x
i
w
i
0,05 0,525 1,75 3,325 5,625 5,5 3,25 1,125
x
= 21,15
xx
i
−
18,65 13,65 8,65 3,65 1,35 6,35 11,35 16,35
2
)( xx
i
−
347,82 186,32 74,82 13,32 1,82 40,32 128,82 267,32
ii
wxx
2
)( −
6,96 13,04 10,48 2,53 0,46 8,06 12,88 8,02
06,6343,62
99
100
2
=⋅=s
Таким образом,
x
=21,15 усл. ден. ед., (усл. ден. ед.)06,63
2
=s
2
.
3) Как установили в пункте 1, распределение случайной величины
Х можно
считать нормальным. В качестве его параметров возьмем оценки
15,21
=
≈
x
a и
94,7
2
=≈σ s полученные в пункте 2. Тогда приближенно вероятность
P(Х ≥ 15) того, что в наудачу выбранный рабочий день дневная выручка опто-
вой базы составит не менее 15 условных денежных единиц, можно вычислить c
использованием функции Лапласа Ф(х). Имеем
Р(X < 15) + Р( X≥ 15) = 1 ⇒ Р(X ≥ 15) = 1 – Р(X < 15) = 1 – F(15),
Но
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
Φ+=
ax
xF 5,0)( и значит
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
Φ+=
a
F
15
5,0)15(. Итак, имеем
.
15
5,0)15(
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
−=≥
a
ФXP Найдем, используя таблицу 1 приложения
.78,07794,02794,05,0)77,0(5,0
)]()([)77,0(5,0
94,7
15,2115
5,0)15(
≈=+=Φ+=
=Φ−=−Φ=−Φ−=
⎟
⎠
⎞
⎜
⎝
⎛
−
Φ−=≥ xxXP
Таким образом, P(Х ≥ 15) ≈ 0,78. Это означает, что в
среднем в 78 из 100
рабочих дней дневная выручка оптовой базы составит не менее 15 усл. ден. ед.
93
Глава 8. Точечные и интервальные оценки параметров
распределений
Имеется два подхода к оцениванию неизвестных параметров распределе-
ний по наблюдениям: точечный и интервальный. Точечный указывает лишь
точку (число), около которой находится оцениваемый параметр; при интер-
вальном находят интервал, который с некоторой вероятностью, задаваемой ис-
следователем, накрывает неизвестное числовое значение параметра.
8.1. Методы построения точечных оценок
Точечное оценивание параметров распределений можно осуществлять сле-
дующими методами: моментов (method of moments); максимального правдопо-
добия (maximum-likelihood method); наименьших квадратов (least-squares
method); минимума χ
2
; робастными (устойчивыми к отклонению модели от за-
данного вида); непараметрическими и др. Рассмотрим некоторые из них.
8.1.1. Метод моментов
Пусть некоторая непрерывная случайная величина ξ описывается моделью
, где . Необходимо оценить неизвестные параметры Θ
модели по выборке конечного объема x
),( Θ
ξ
xp
),...,(
1 K
θθ=Θ
1
, … , x
n
, полученной из генеральной со-
вокупности. Суть методо моментов состоит в приравнивании оценок моментов
(начальных, центральных) эмпирического распределения соответствующим
теоретическим моментам выбранной модели, являющимся функциями неиз-
вестных параметров модели, и затем решении полученной системы уравнений.
Число уравнений в системе определяется количеством искомых параметров.
Начальные и центральные теоретические моменты k-го порядка
могут быть
получены из выражений
)(),( Θν=Θ=ν
∫
∞
∞−
ξ k
k
k
dxxpx
, ,
)(),()( Θµ=Θν−=µ
∫
∞
∞−
ξ k
k
kk
dxxpx
а их оценки
k
ν
)
и
k
µ
)
− по выборке x
1
, … , x
n
. Полагая, что
k
ν
)
и
k
µ
)
являются со-
стоятельными оценками моментов ν
k
и µ
k
, приравниваем их друг другу. В ре-
зультате получим систему
⎩
⎨
⎧
µ=Θµ
ν=Θν
,)(
,)(
kk
kk
)
)
(8.1)
число уравнений в которой должно быть равным числу
K неизвестных пара-
метров θ
i
, (
K
i ,...,1= ). Решив систему (8.1) относительно неизвестных парамет-
ров Θ, получим М-оценки
)(M
i
θ
)
, (
K
i ,...,1
=
).
Если случайная величина ξ является дискретной, то вместо плотности вероят-
ности
используем функцию вероятности
),( Θ
ξ
xp
iii
pxPxp
=
Θ
=ξ=
Θ
ξ
),(),(
, а
начальные и центральные теоретические моменты определяем по формулам:
94

)(
1
Θν==ν
∑
=
k
n
i
i
k
ik
px , )()(
1
Θµ=−=µ
∑
=
k
n
i
iik
pxx .
Замечание 8.1. Вопрос о том, какие начальные и центральные моменты
включать в систему (8.1) следует решать, руководствуясь конкретными целями
исследования и сравнительной простотой форм зависимостей моментов от па-
раметров. На практике, как правило, ограничиваются четвертыми моментами.
Предложение 8.1. Пусть решение системы (8.1) существует и функции
2111
)(
)(
,,...,1),,,,,,(
21
KKKKivv
KK
M
i
M
i
+==µµθ=θ
)
K
)
)
K
)
)
)
непрерывны в точке
)...,,,...,,(
21
11 KK
vvm
µ
µ
=
. Тогда оценки, полученные по ме-
тоду моментов, состоятельны. #
Пример 8.1. Найдем оценку параметра λ закона распределения Пуассона.
Известно, что для случайной величины ξ, распределенной по закону Пуас-
сона,
λ=ξ][
M
. Поэтому для нахождения единственного параметра λ достаточ-
но приравнять теоретический ν
1
и эмпирический
1
ν
)
начальные моменты перво-
го порядка. Момент
x
M
=ν
)(
1
)
, следовательно, оценка метода моментов парамет-
ра λ есть выборочное среднее
x
.
Пример 8.2. Случайная величина ξ имеет нормальный закон распределения
N(a, σ
2
), при этом числовые значения параметров a и σ
2
неизвестны. Найдем
оценки метода моментов для этих параметров.
Используя формулу (3.5), выразим моменты
ν
1
и
ν
2
через a и σ
2
:
∫
∞
∞−
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
−
=
πσ
=ν 2,1,
2
1
2
2
1
kdxex
ax
k
k
.
Система (8.1) в данном случае примет вид
⎩
⎨
⎧
σ+=ν
=ν
.
,
22
2
1
a
a
Отсюда получаем
M-оценки
xx
n
a
n
i
i
M
==ν=
∑
=1
1
)(
1
)
)
,
2
1
22
1
22
12
)(2
)(
11
σ=−=−=ν−ν=σ
∑∑
==
)
))
)
n
i
i
n
i
i
M
xx
n
xx
n
.
Замечание 8.2. Оценки метода моментов обычно состоятельны, однако по
эффективности они не являются «наилучшими», т.к. их эффективность )(
)(M
n
e θ
)
часто значительно меньше единицы. Тем не менее, метод моментов часто ис-
пользуется на практике, благодаря сравнительно простым вычислениям. Это
объясняется тем, что для большинства статистических моделей, соответствую-
щих основным вероятностным распределениям, система (8.1) без труда решает-
ся в каждом конкретном случае.
95

8.1.2. Метод максимального правдоподобия
Основным методом получения оценок параметров генеральной совокупно-
сти по выборочным данным является
метод максимального правдоподобия
(ММП). Пусть в результате статистического наблюдения получена выборка
x
1
, … , x
n
, которая описывается некоторой моделью
),(
Θ
ξ
xp
, где ),...,(
1 K
θ
θ
=Θ .
Определение 8.1. Функция (вообще говоря, случайная величина)
∏
=
ξ
Θ=Θ
n
i
in
xpxxL
1
1
),(),,...,( . (8.2)
называется
функцией правдоподобия. Функцию называют лога-
рифмической функцией правдоподобия
.
),,...,(ln
1
Θ
n
xxL
Определение 8.2. Согласно методу максимального правдоподобия искомые
ML-оценки
)(ML
Θ
)
определяются из условия
),,...,(max),,...,(
1
)(
1
Θ=Θ
Θ
n
ML
n
xxLxxL
)
. (8.3)
При условии независимости вариантов
x
i
плотность (8.2) вероятности со-
вместного появления результатов выборки
x
1
, … , x
n
является мерой правдопо-
добности
получения наблюдений x
1
, … , x
n
. И оценки
)(ML
Θ
)
таковы, что имею-
щиеся наблюдения
x
1
, … , x
n
наиболее правдоподобные.
Замечание 8.3. Если функция правдоподобия ) является диф-
ференцируемой по переменным
x
,,...,(
1
Θ
n
xxL
1
, … , x
n
, то оценка наибольшего правдоподо-
бия удовлетворяет системе уравнений
Ki
xxL
i
Kn
,...,1,0
),...,;,...,(
11
=∀=
θ∂
θθ∂
.
Эта система представляет собой известное из курса математического анализа
необходимое условие экстремума функции многих переменных.
Нахождение
)(ML
Θ
)
упрощается, если максимизировать не саму функцию L,
а
L
ln , поскольку максимум обеих функций достигается при одних и тех же
значениях Θ. Поэтому для отыскания вектора оценок параметров
)(ML
Θ
)
надо
вместо (8.3) решить систему (при
2≥
K
) уравнений правдоподобия, получае-
мую приравниваем частных производных по параметрам θ
i
к нулю:
Ki
L
i
,...,1,0
ln
=∀=
θ∂
∂
)
. (8.4)
а затем отобрать то решение, которое обращает функцию
L
ln в максимум.
Для дискретной случайной величины ξ вместо плотности вероятности
используем функцию вероятности
),( Θ
ξ
xp
iii
pxPxp =Θ=
ξ
=
Θ
ξ
),(),(
.
Пример 8.3. Найти ML-оценку для вероятности p наступления некоторого
события
A по числу m появлений этого события в n независимых испытаниях.
96
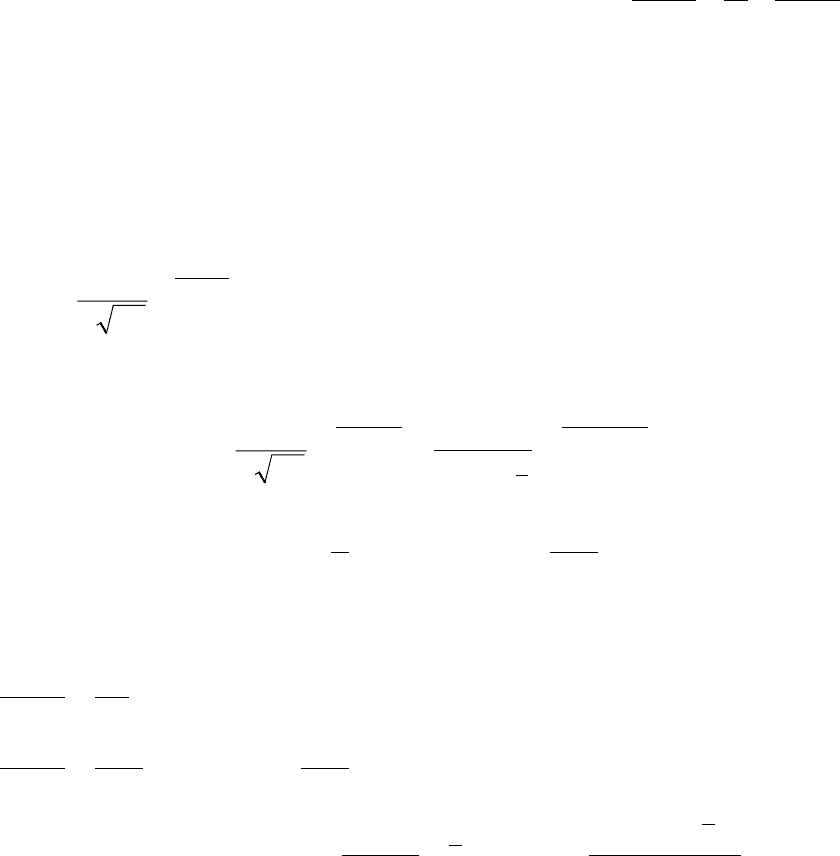
Решение. Составим функцию правдоподобия:
mnm
mnm
n
ppppppppxxL
−
−
−=−−= )1()1)...(1(...),,...,(
1
4434421321
.
Тогда
)1ln()(lnln
p
mn
p
m
L
−
−+= и согласно (8.4)
0
1
ln
=
−
−
−=
p
mn
p
m
dp
Ld
,
откуда
nmp
ML
/
)(
=
)
. Таким образом, ML-оценкой вероятности p является час-
тость
nmw
/
= этого события.
Пример 8.4. Найдем методом максимального правдоподобия оценки пара-
метров
a и σ
2
нормального закона распределения по выборке x
1
, … , x
n
.
Плотность вероятности нормально распределенной случайной величины ξ
2
2
2
)(
2
1
)(
σ
−
−
ξ
πσ
=
ax
exp .
Тогда функция правдоподобия примет вид:
2
1
2
2
2
2
)(
2
1
2
)(
2
1
)2(
1
2
1
),,,...,(
σ
−
−
=
σ
−
−
∑
=
πσ
=
πσ
=σ
∏
n
i
i
i
ax
n
n
n
i
ax
n
eeaxxL
.
Логарифмируя, получим:
∑
=
−
σ
−π+σ−=
n
i
i
ax
n
L
1
2
2
2
)(
2
1
)]2ln([ln
2
ln .
Для нахождения параметров
a и σ
2
надо согласно (8.4) решить систему
уравнений правдоподобия:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
σ
−−
σ
=
σ∂
∂
=−
σ
=
∂
∂
∑
∑
=
=
,0
2
)(
2
1ln
,0)(
1ln
1
2
2
42
1
2
n
i
i
n
i
i
n
ax
L
ax
a
L
откуда ML-оценки равны:
x
n
x
a
n
i
i
ML
==
∑
=1
)(
)
,
n
xx
n
i
i
ML
∑
=
−
=σ
1
2
)(
2
)(
)
.
Таким образом, ML-оценками математического ожидания a и дисперсии σ
2
нормально распределенной случайной величины являются соответственно вы-
борочная средняя арифметическая и выборочная дисперсия.
Важность ММП связана с его оптимальными свойствами. Так, если для па-
раметра θ существует эффективная оценка
ef
n
θ
)
, то оценка максимального
правдоподобия единственная и равна этой эффективной оценке
ef
n
θ
)
. Кроме то-
го, при достаточно общих условиях оценки максимального правдоподобия яв-
ляются состоятельными, асимптотически эффективными и имеют асим-
птотически нормальное распределение.
Замечание 8.4. Основной недостаток ММП – трудоемкость вычисления
оценок, связанных с решением уравнений правдоподобия, чаще всего нелиней-
97

ных. Существенно также и то, что для построения ML-оценок и обеспечения их
«хороших» свойств необходимо точное знание типа анализируемого закона
распределения p
ξ
(x, Θ), что во многих случаях практически нереально.
8.1.3. Метод наименьших квадратов
Метод наименьших квадратов (МНК) – один из наиболее простых прие-
мов построения оценок. Суть его заключается в том, что оценка определяется
из условия минимизации суммы квадратов отклонений выборочных данных от
определяемой оценки. Дадим постановку задачи для линейной модели в общем
случае. Запишем линейную модель в виде
ε+Θ= X
y
,
где y − вектор-столбец наблюдений y
1
, … , y
n
размерности n,
X − матрица известных коэффициентов
Knij
x
×
}{
)(
K
n >
,
Θ− вектор-столбец неизвестных параметров
K
θ
θ
,...,
1
размерности K,
ε − вектор-столбец случайных величин
n
ε
ε
,...,
1
размерности n, которые не-
коррелированы, имеют нулевое математическое ожидание и дисперсию σ
2
.
Определение 8.3. Метод наименьших квадратов состоит в минимизации
скалярной суммы квадратов
)()( Θ−Θ−=
XyXy
T
Q (8.5)
по компонентам
K
θ
θ
,...,
1
вектора Θ. Необходимым условием обращения (8.5) в
минимум является условие
Ki
Q
i
K
,...,1,0
),...,(
1
==
θ∂
θθ∂
.
Выполняя дифференцирование, получаем
, откуда нахо-
дим вектор LS-оценок:
0)(2 =Θ− XyX
T
yXXX
TTLS 1)(
)(
−
=Θ
)
. Предполагается, что матрица
невырождена и, следовательно, может быть обращена.
XX
T
Пример 8.5. Найдем оценку метода наименьших квадратов
)(LS
θ
)
для мате-
матического ожидания случайной величины ξ по выборке x
1
, … , x
n
.
Согласно методу наименьших квадратов оценка
)(LS
θ
)
находится из условия
минимизации суммы квадратов отклонений выборочных значений x
i
от значе-
ния искомой МНК-оценки:
.
min)()(
1
2)()(
→θ−=θ
∑
=
n
i
LS
i
LS
xf
))
Используем необходимое условие экстремума
∑
=
=θ−−=
θ
n
i
LS
i
LS
x
d
df
1
)(
)(
0)(2
)
)
, откуда x
n
x
n
i
i
LS
==θ
∑
=1
)(
)
,
т.е. МНК-оценка математического ожидания есть выборочная средняя.
98

Замечание 8.5. МНК, отличаясь по подходу от метода максимального
правдоподобия, и, обладая своими собственными оптимальными свойствами,
совпадает с ММП в важном случае нормально распределенных наблюдений.
МНК получил самое широкое распространение в практике статистических ис-
следований, т.к.:
- не требует знания закона распределения выборочных данных;
- имеет простую вычислительную реализацию.
В отличие от
ММП, МНК в общем случае не обладает даже асимптотиче-
скими оптимальными свойствами. Однако в одном очень важном классе ситуа-
ций он, даже при малых выборках, обладает свойством оптимальности. А
именно, если все наблюдения (варианты) x
i
имеют одинаковые дисперсии, вза-
имно некоррелированы и являются линейными функциями неизвестных пара-
метров, то МНК дает несмещенные оценки, которые имеют минимальную дис-
персию (т.е. обладают свойством эффективности).
В последние годы развиваются робастные (или устойчивые) и непарамет-
рические методы оценивания. Они позволяют находить оценки, хотя и не яв-
ляющиеся наилучшими
в рамках предполагаемого закона распределения, но
обладающие достаточно устойчивыми свойствами при отклонении реального
закона от предполагаемого. Например, устойчивой оценкой математического
ожидания по конечной выборке является медиана этой выборки.
8.2. Неравенство Рао–Крамера–Фреше
Рассмотрим более подробно вопрос об эффективности оценок. В определе-
нии 7.4 дано понятие эффективности оценки, но как ее определять не показано.
Пусть p
ξ
(x, θ) − плотность вероятности случайной величины ξ, если ξ − непре-
рывна, и
),(),( θ=ξ
=
θ
ξ ii
xPxp
, если ξ − дискретна, θ − неизвестный параметр.
Предложение 8.2. При выполнении функцией p
ξ
(x, θ) достаточно общих
условий регулярности: дифференцируемости по θ, независимости области оп-
ределения от θ и т.д., являющихся достаточно общими, справедливо неравен-
ство Рао–Крамера–Фреше (неравенство информации):
]'[min
)(
1
][
'
θ=
θ
≥θ
∈θ
D
nI
D
S
)
, (8.6)
где
][θ
)
D
− дисперсия оценки
θ
)
параметра θ; n − объем выборки; I(θ) − количе-
ство информации Фишера о параметре, содержащееся в единичном наблюде-
нии и определяемое формулами:
- в дискретном случае
∑
=
θ
θϕ
⎥
⎦
⎤
⎢
⎣
⎡
θϕ
′
θϕ
=
⎥
⎦
⎤
⎢
⎣
⎡
θ
θϕ
=θ
n
i
iX
iX
iX
X
x
x
x
d
xd
MI
1
2
),(
),(
),(
),(ln
)(
,
- в непрерывном случае
∫
∞
∞−
θ
θθϕ
⎥
⎦
⎤
⎢
⎣
⎡
θϕ
′
θϕ
=
⎥
⎦
⎤
⎢
⎣
⎡
θ
θϕ
=θ dx
x
x
d
xd
MI
X
X
X
X
),(
),(
),(
),(ln
)(
2
2
. #
99
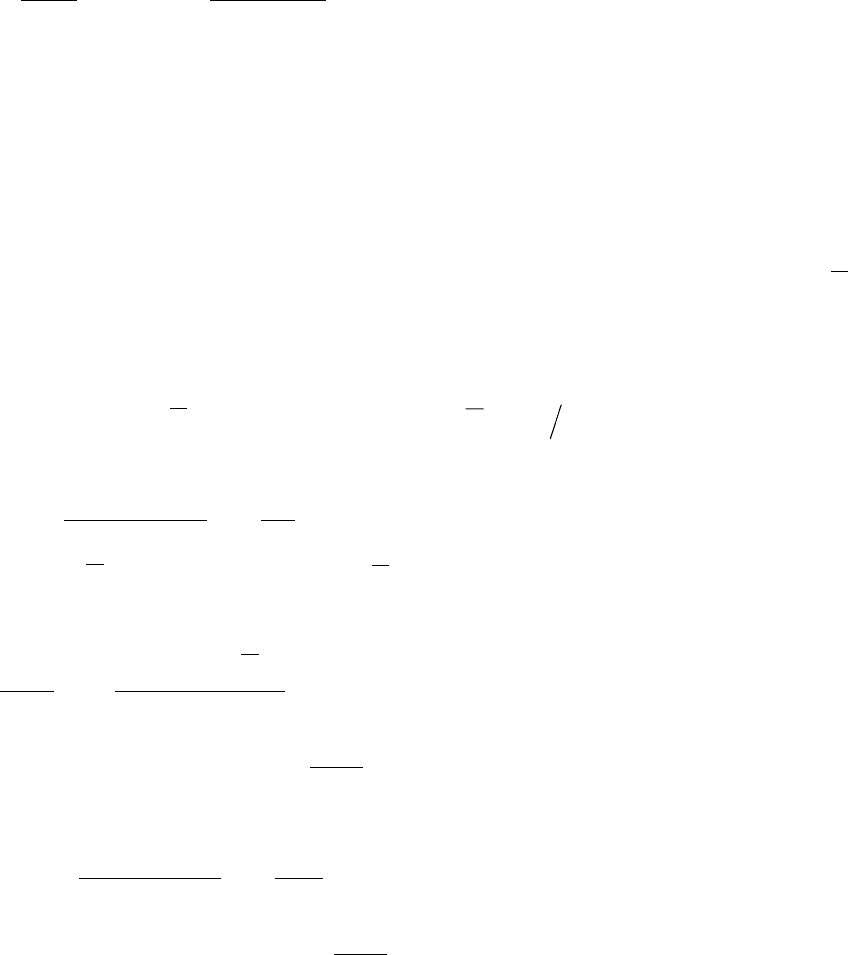
Поэтому
1
][)(
1
][min
][
1
)(
'
≤
θθ
=θ
θ
=θ
Θ∈θ
))
)
DnI
D
D
e
. (8.7)
Если
1)( =θ
)
e
, то
θ
)
− эффективная оценка параметра θ в классе Θ всех его не-
смещенных оценок. Т.е. неравенство информации (8.6) позволяет найти тот ми-
нимум
, который должна иметь дисперсия оценки , чтобы быть
эффективной оценкой.
]'[min
'
θ
Θ∈θ
D
2
θ
σ
)
Пример 8.6. Убедиться в том, что найденная методом моментов по случай-
ной выборке из генеральной совокупности с распределением N(a, σ
2
) оценка
X
параметра a является эффективной в классе несмещенных оценок, а оценка s
2
параметра σ
2
является, после исключения смещения, асимптотически эффек-
тивной.
Решение. Оценка
X − несмещенная, и
nXD
2
][ σ=
. Предположив, что σ
2
известна, и, используя формулу (8.7), с учетом нормальности распределения
2
2
1
),(ln
)(
σ
=
⎥
⎦
⎤
⎢
⎣
⎡
ϕ
=
da
axd
MaI
X
,
получим, что
1)( =Xe
. Следовательно,
X − эффективная оценка.
Оценка дисперсии
2
n
σ
)
смещенная; исключив смещение, получим оценку
1
)(
1
1
2
22
−
−
=σ
−
=
∑
=
n
XX
n
n
s
n
i
i
n
)
,
дисперсия которой равна
1
2
][
4
2
−
σ
=
n
sD
. Считая, что a известно, и, используя
(8.7), в которой, с учетом нормальности распределения,
4
2
2
2
2
1
),(ln
)(
σ
=
⎥
⎦
⎤
⎢
⎣
⎡
σ
ϕ
=σ
d
axd
MI
X
,
получим, что эффективность
1
1
)(
2
<
−
=
n
n
se
, а асимптотическая эффективность
. Следовательно, s
1)(lim)(
22
0
==
∞→
sese
n
2
− асимптотически эффективная оценка.
Замечание 8.6. В заключение обсуждения методом нахождения оценок,
отметим, что, даже имея большие объемы экспериментальных данных, мы не
имеем возможности указать точные значения оцениваемых параметров, а опре-
деляем лишь их оценки, близкие «в среднем», или «в большинстве случаев».
Поэтому важной задачей является, рассматриваемое далее, определение точно-
сти и достоверности найденных оценок.
100
