Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие
Подождите немного. Документ загружается.


Таблица 9.2
№№
[]
1
,
+ii
xx
n
i
p
i
np
i
(n
i
−np
i
)
2
i
ii
np
npn
2
)( −
1 94 – 100 3 0,017 1,7
10 7,6 5,76 0,758
111
2 100 – 106 7 0,059 5,9
3 106 – 112 11 0,141 14,1 9,61 0,682
4 112 – 118 20 0,228 22,8 7,84 0,344
5 118 – 124 28 0,247 24,7 10,89 0,441
6 124 – 130 19 0,182 18,2 0,64 0,035
7 130 – 136 10 0,087 8,7
12 11,6 0,16 0,014
8 136 – 142 2 0,029 2,9
Всего 100 0,990 99,0
−
ψ
calc
= 2,27
9.2.2. Критерий согласия Колмогорова−Смирнова
Критерий согласия Колмогорова
−
Смирнова проверяет гипотезу о согласии
при небольшом объеме выборки, когда F
mod
(x, Θ) известна полностью, т. е. из-
вестны и параметры модели. Рассмотрим последовательность критерия.
1-й шаг. Формулирование основной H
0
и альтернативной H
1
гипотез (9.2).
2-й шаг. Задание уровня значимости α.
3-й шаг. Формирование критической статистики.
В критерии Колмогорова−Смирнова для введения меры отклонения эмпи-
рического и модельного распределений используются статистика вида
),()(max
mod
Θ−= xFxFD
n
x
n
. В качестве статистмки ψ
cr
используем функцию
ψ
cr
= ),()(max
mod
Θ−⋅=⋅ xFxFnDn
nxn
. (9.4)
Предложение 9.1. Какова бы ни была функция распределения F
mod
(x, Θ)
непрерывной случайной величины ξ, распределение
ψ
cr
имеет пределом функ-
цию
, не зависящую от вида функции . #
∑
∞
−∞=
ψ−
−=ψΚ
i
i
i
cr
cr
e
22
2
)1()(
),(
mod
ΘxF
Если F
mod
(x, Θ) задана с точностью до неизвестных параметров Θ и они
оцениваются по конечной выборке размера n, то предельное распределение ста-
тистики
nD
n
уже зависит от F
mod
(x, Θ). При этом статистика ψ
cr
будет зави-
сеть только от формы распределения F
mod
(x, Θ). Если в модельном распределе-
нии есть только параметры сдвига и масштаба, то применимость критерия Кол-
могорова–Смирнова корректна.
4-й шаг. Из определения функции распределения следует, что при доста-
точно большом n и любом ψ
cr
> 0 вероятность того, что
nD
n
примет значение,
меньшее ψ
cr
, будет иметь вид
α=−−=ψΚ−=ψ≥
∑
∞
−∞=
ψ−
i
i
i
crcrn
cr
enDP
22
2
)1(1)(1}{
.
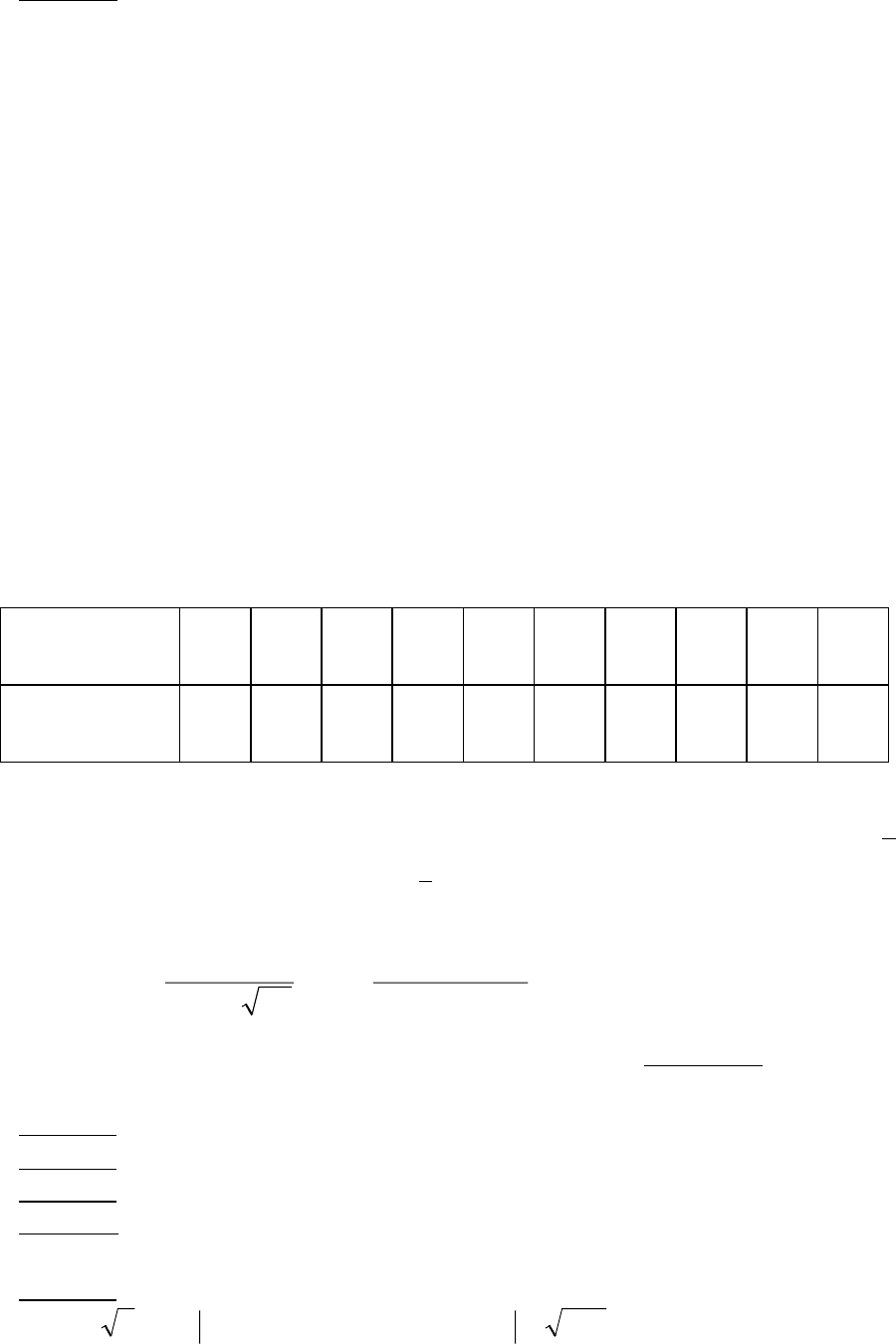
Значение ψ
cr.u
при заданном α можно найти в статистических таблицах.
Нижняя критическая граница в данном критерии не используется.
5-й шаг. ψ
calc
определяется из (9.4) подстановкой значений n и D
n
, для кон-
кретных эмпирических данных. Если выполняется условие ψ
calc
≤ ψ
cr.u
, то гипо-
теза о согласии эмпирического распределения и модельного принимается.
Замечание 9.5. Для большого объема выборки, ее нужно сгруппировать и
значения F
n
(x) и F
mod
(x, Θ) определять на границах интервалов группирования.
Применение критерия в принципе возможно лишь тогда, когда теоретиче-
ская функция распределения F
mod
(x, Θ) задана полностью. Но такой случай на
практике встречается весьма редко. Обычно из теоретических соображений из-
вестен лишь вид функции распределения, а ее параметры определяются по эм-
пирическим данным.
Пример 9.3. Даны результаты исследования отклонения фактического вы-
пуска продукции (тыс. руб.) от планового (план – 1000 тыс. руб.) 400 предпри-
ятий в группированном виде (табл. 9.3). Проверить гипотезу о согласии эмпи-
рического распределения с нормальной моделью по критерию Колмогорова–
Смирнова при α = 0,05.
Таблица 9.3
Фактический
выпуск
950-
960
960-
970
970-
980
980-
990
990-
1000
1000-
1010
1010-
1020
1020-
1030
1030-
1040
1040-
1050
Количество
предприятий
5 15 60 72 80 60 55 30 20 3
Решение. Параметры нормального закона – математическое ожидание a и
дисперсия σ
2
неизвестны, поэтому заменяем их на выборочную среднюю
x
и
выборочную дисперсию
2
σ
)
, равные 45,99
=
x
и
998,361026,19
22
==σ
)
. Следо-
вательно, распределение нормальной модели будет иметь вид
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
π
=Θ
996,723
)45,997(
exp
2026,19
1
),(
2
mod
x
xf ,
⎟
⎠
⎞
⎜
⎝
⎛
−
Φ+===Θ
∫
∞−
ξ
03,19
45,997
5,0)03,19;45,997;()(),(
mod
x
xFdyypxF
N
x
.
1-й шаг. Формулирование основной H
0
и альтернативной H
1
гипотез (9.2).
2-й шаг. α = 0,05.
3-й шаг. Вид ψ
cr
и ее распределение находим из (9.4) и предложения 9.1.
4-й шаг. Из таблицы значений функции Колмогорова для уровня значимо-
сти α = 0,05 определяем ψ
cr.u
= 1,36.
5-й шаг. Используя данные таблицы 9.4, находим
ψ
calc
= .
634,00317,0400)03,19;45,997;()(max =⋅=−⋅ xFxFn
Nn
x
112

Т.к. ψ
calc
>
ψ
cr.u
, то гипотеза H
0
отвергается с ошибкой первого рода α = 0,05.
Результаты вычисления статистики
ψ
calc
сведены в табл. 9.4.
Таблица 9.4
Результаты вычисления ψ
calc
для примера 9.3
113
][
1
,
+ii
xx
F
n
(x)
σ
−
=
)
xx
z
i
i
Φ(z
i
)
)(5,0
);;(
mod
i
z
xxF
Φ+=
=σ
)
);;()(
mod
σ−
)
xxFxF
n
0
–∞
–0,5 0 0
–∞ ÷ 960
0,0125 –1,97 –0,4756 0,0244 0,0119
960 ÷ 970
0,05 –1,44 –0,4222 0,0778 0,0278
970 ÷ 980
0,2 –0,92 –0,3159 0,1841 0,0159
980 ÷ 990
0,38 –0,39 –0,1517 0.3483 0,0317
990 ÷ 1000
0,58 0,13 0,0517 0,5517 0,0283
1000 ÷ 1010
0,73 0,66 0,2454 0,7454 0,0154
1010 ÷ 1020
0,8675 1,18 0,3810 0,8810 0,0135
1020 ÷ 1030
0,9425 1,71 0,4564 0,9564 0,0139
1030 ÷ 1040
0,9925 2,23 0,4871 0,9871 0,0054
1040 ÷ ∞
1,0
∞
0,5 1,0 0
9.3. Критерии однородности
Основные гипотезы однородности можно записать в виде:
)(...)()(:
210
xFxFxFH
l
F
=== ; ; .
l
a
aaaH === ...:
210
22
2
2
10
...:
l
H σ==σ=σ
σ
Рассмотрим два наиболее распространенных статистических критерия про-
верки гипотез об однородности анализируемых генеральных совокупностей.
9.3.1. Критерий однородности Смирнова
Пусть имеются две выборки объемами n
1
и n
2
. Элементы каждой выборки
независимы, непрерывны и сгруппированы в L интервалов. Проверим, принад-
лежат ли выборки одной генеральной совокупности. Критерий Смирнова при-
меним если: данные представлены в группированном виде; min(n
1
, n
2
) > 50.
1-й шаг. Формирование основной и альтернативной гипотез
)()(:
0
yFxFH
ηξ
=
,
)()(:
1
yFxFH
ηξ
≠
.
2-й шаг. Задание уровня значимости α.
3-й шаг. Формирование критической статистики
∑
=
ν+µ
ν−µ
L
i
ii
ii
nn
nn
1
2
21
21
)//(
ψ
cr
= ,
где µ
i
, ν
i
− количество попаданий в i-й интервал группирования соответственно
первой и второй выборок. Если
nnn
=
=
21
, то ψ
cr
=
∑
=
ν+µ
ν−µ
L
i
ii
ii
1
2
)(
.
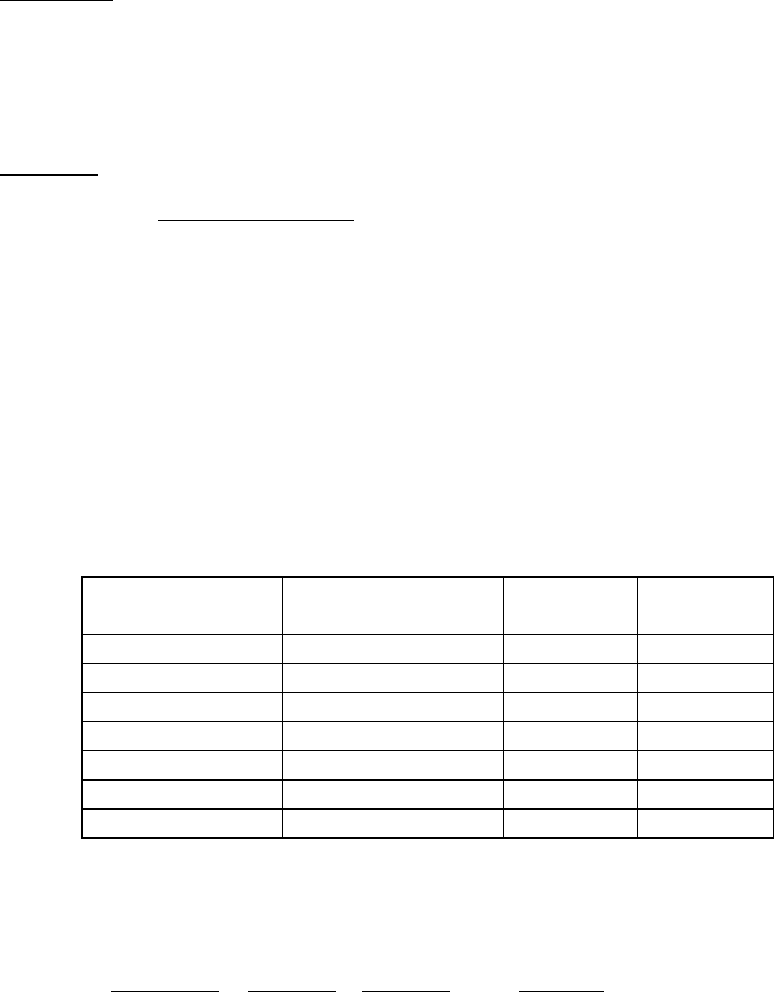
Предложение 9.2. Предельное распределение критической статистики ψ
cr
при неограниченном росте объемов выборок n
1
, n
2
и в условиях справедливости
проверяемой гипотезы H
0
стремится к χ
2
−распределению с (L – 1) числом сте-
пеней свободы, т. е.
(ψ
F
nn ∞→
21
,
lim
cr
) . # )1(
2
−χ= L
4-й шаг. Определение критической точки статистического критерия
ψ
cr.u
= . Критерий Смирнова является односторонним. Области не-
правдоподобно малых значений статистики ψ
)1(
2
%100
−χ
⋅α
L
cr
нет. Чем меньше расчетное зна-
чение критической статистики, тем более благоприятные условия складывают-
ся для принятия гипотезы об однородности двух выборок.
5-й шаг. Определение расчетного значения критической статистики
∑
=
ν+µ
ν−µ
L
i
ii
ii
nn
n
1
2
21
21
)//(
n .
ψ
calc
=
Если
ψ
calc
≤ ψ
cr.u
, то гипотеза H
0
верна, в противном случае H
0
отвергается.
Пример 9.4. В банке в течение двух дней проводилось исследование вре-
мени обслуживания клиентов. Данные представлены в табл. 9.5, где µ
i
, ν
i
−
времена обслуживания клиентов в первый и второй дни. Проверить однород-
ность двух группированных выборок – времени обслуживания в первый и вто-
рой дни по критерию Смирнова при уровне значимости α = 0,1.
Таблица 9.5
Статистические данные времени обслуживания клиентов в банке
Номер интервала
г
ру
ппи
р
ования i
Время обслужива-
ния
(
мин
)
µ
i
(1-й день) ν
i
(2-й день)
1 10 – 12 2 2
2 12 – 14 4 4
3 14 – 16 8 9
4 16 – 18 12 13
5 18 – 20 16 16
6 20 – 22 10 8
7 22 – 24 3 3
Решение. Верхняя критическая точка ψ
cr.u
= . Расчетное
значение критической статистики равно
645,10)6(
2
%10
=χ
ψ
calc
=
()
321,0
6
)33(
...
8
)44(
4
)22(
222
1
2
=
−
++
−
+
−
=
ν+µ
ν−µ
∑
=
L
i
ii
ii
.
Условие ψ
calc
≤ ψ
cr.u
выполняется, и H
0
верна с ошибкой первого рода 10%.
9.3.2. Критерий Вилкоксона−Манна−Уитни
Критерий Вилкоксона
−
Манна
−
Уитни является ранговым и применяется
для проверки однородности двух генеральных совокупностей понимаемой в
смысле отсутствия различий в значениях параметров
положения (средних зна-
114
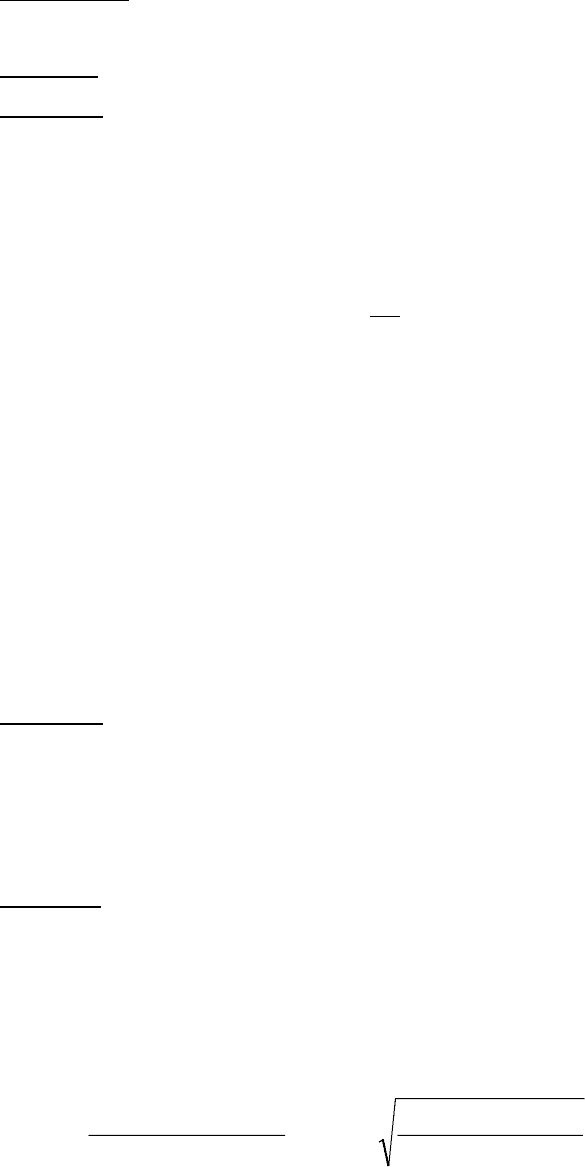
чений, медиан) соответствующих распределений (но не тождественного сов-
падения распределений, как в предыдущем критерии). Т.е. проверяется гипотеза
типа H
0
a
. Распределения проверяемых генеральных совокупностей неизвестны.
Статистические данные должны быть представлены в негруппированном виде.
В критерии возможны два случая. Рассмотрим их последовательно.
115
),...,
2
1 n
yy
Случай А. Пусть имеются две выборки независимых непрерывных случай-
ных величин
,
(
, где
),...,(
1
1 n
xx
25
1
≤
n
,
25
2
≤
n
.
1-й шаг. Формирование основной и альтернативной гипотез
, .
)()(:
0
yFxFH
ηξ
= )()(:
1
yFxFH
ηξ
≠
2-й шаг. Задание уровня значимости α.
3-й шаг. Формирование критической статистики, равной ψ
cr
= ,
где
− ранги элементов выборки меньшего объема . Суммирование
рангов
осуществляется по элементам меньшей выборки.
∑
+
=
21
1
)1(
nn
i
i
R
)1(
i
R
)(
21
nn ≤
)1(
i
R
Предложение 9.3. В условиях справедливости гипотезы H
0
статистика
ψ
cr
= при и
∑
+
=
21
1
)1(
nn
i
i
R
∞→
1
n
0lim
2
1
1
>=
∞→
c
n
n
n
стремится к нормальному распре-
делению с математическим ожиданием a = M[ψ
cr
] = и диспер-
сией σ
2/)1(
211
++ nnn
2
= D[ψ
cr
] = #
12/)(
2121
nnnn +
Для принятия решения об однородности двух выборок по критерию Вил-
коксона−Манна−Уитни необходимо выполнить следующие действия:
1) Проанализировать объемы выборок n
1
и n
2
, сравнить их между собой. Мень-
шую выборку будем считать первой. Пусть n
1
− объем меньшей выборки;
2) Из двух выборок составляем общий вариационный ряд с обозначением ран-
гов вариант. Если в обеих выборках есть одинаковые варианты, то в общем ва-
риационном ряду первыми записываются варианты меньшей (первой) выборки.
4-й шаг. По статистическим таблицам критических точек распределения
Вилкоксона−Манна−Уитни для уровня значимости а находим нижнюю крити-
ческую точку ψ
cr.l
= , где )),(
212/
nn
α
ω ,(
212/
nn
α
ω
− квантиль распределения
Вилкоксона−Манна−Уитни. Верхняя критическая точка равна
ψ
cr.u
=
121
)1( nnn
+
+
− ψ
cr.l
. (9.5)
5-й шаг. Вычисление расчетного значения критической статистики ψ
calc
=
осуществляется суммированием рангов вариант первой выборки
в общем вариационном ряду. Если выполняется условие ψ
∑
+
=
21
1
)1(
nn
i
i
R
)1(
i
R
cr.l
≤ ψ
calc
≤ ψ
cr.u
, то
гипотеза H
0
верна, в противном случае H
0
отвергается.
Случай Б. Объем хотя бы одной из выборок больше 25. Отличие данного
случая от предыдущего состоит только в вычислении ψ
cr.l
на четвертом шаге:
ψ
cr.l
=
⎥
⎦
⎤
⎢
⎣
⎡
++
−
−++
α−
12
)1(
2
1)1(
2121
2/1
121
nnnn
u
nnn
, (9.6)

где u
1–α/2
− квантиль нормального распределения уровня 1 − α/2.
Замечание 9.6. можно также находить в виде
2/1 α−
u
⎟
⎠
⎞
⎜
⎝
⎛
α−
Φ=
α−
2
1
arg
2/1
u
,
где Φ(⋅) − функция Лапласа, табличные значения которой известны.
Пример 9.5. Объемы дневных продаж овощных магазинов в двух районах
области представлены выборками (табл. 9.6, 9.7) x
i
, y
i
, ( 27,...,1
=
i ) (в тыс. руб.).
Проверить гипотезу об однородности двух выборок по критерию Вилкоксона–
Манна–Уитни при уровне значимости α = 0,05.
Таблица 9.6
17 13 22 9 20 9 20 9 22
20 21 21 22 19 23 14 20 19
X:
17 11 8 21 10 20 18 11 15
Таблица 9.7
17 13 22 9 20 10 16 9 21
15 21 21 22 18 21 15 20 18
Y:
17 11 8 21 17 15 18 11 19
Решение. Поскольку
2527
21
>
=
=
nn
, то воспользуемся алгоритмом для
случая Б. Будем считать первой выборку X. Составим из двух выборок общий
вариационный ряд (табл. 9.8), проставляя сразу ранги R
k
, (
21
,...,1 nnk
+
=
) эле-
ментам объединенного ряда. Принадлежность элемента той или иной выборке
обозначим с помощью индекса ранга.
Таблица 9.8
Элемент ряда 8
X
8
Y
9
X
9
X
9
X
9
Y
9
Y
10
X
10
Y
R
k
1 2 3 4 5 6 7 8 9
Элемент ряда 11
X
11
X
11
Y
11
X
13
X
13
Y
14
X
15
X
15
Y
R
k
10 11 12 13 14 15 16 17 18
Элемент ряда 15
Y
15
Y
16
Y
17
X
17
X
17
Y
17
Y
17
Y
18
X
R
k
19 20 21 22 23 24 25 26 27
Элемент ряда 18
Y
18
Y
18
Y
19
X
19
X
19
Y
20
X
20
X
20
X
R
k
28 29 30 31 32 33 34 35 36
Элемент ряда 20
X
20
X
20
Y
20
Y
21
X
21
X
21
X
21
Y
21
Y
R
k
37 38 39 40 41 42 43 44 45
Элемент ряда 21
Y
21
Y
21
Y
22
X
22
X
22
X
22
Y
22
Y
23
X
R
k
46 47 48 49 50 51 52 53 54
116
По таблице значений функции Лапласа для α = 0,05 найдем квантиль
. Из (9.5), (9.6), получим ψ
96,1)475,0(arg
2/1
=Φ=
α−
u
cr.l
и ψ
cr.u
:
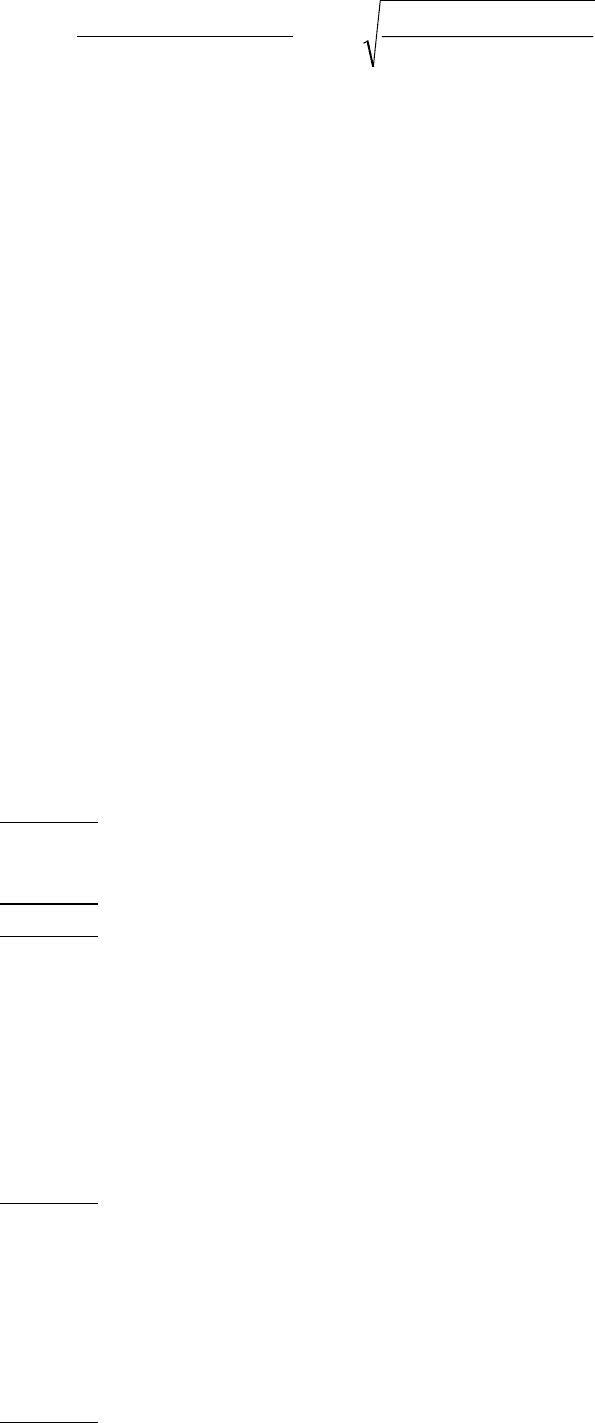
ψ
cr.l
=
7,628
12
)12727(2727
96,1
2
127)12727(
=
++⋅
−
−⋅++
,
ψ
cr.u
= 3,8567,62827)12727(
=
−⋅++ .
Вычислим расчетное значение критической статистики:
ψ
calc
= .
734545150431
54
1
)1(
1
)1(
21
=+++++==
∑∑
=
+
=
K
i
i
nn
i
i
RR
Условие ψ
cr.l
≤ ψ
calc
≤ ψ
cr.u
выполняется, следовательно, гипотеза H
0
верна.
9.4. Гипотезы о числовых характеристиках случайных величин
В общем случае гипотезы о числовых характеристиках случайных величин
имеют вид:
00
: ∆
∈
ΘH
, где
),...,(
1 K
θ
θ
=
Θ
− некоторый вектор параметров (но
может быть и скаляром, т.е.
1
θ
=
Θ
), а ∆
0
− область конкретных значений этих
параметров, которая может состоять из точки. Рассмотрим некоторые из крите-
риев проверки гипотез о числовых характеристиках случайных величин.
9.4.1. Проверка гипотез о равенстве дисперсий случайной величины
при известных математических ожиданиях
Пусть имеются две выборки ( ), ( ) случайных величин ξ и
η из нормальных генеральных совокупностей и пусть математические ожида-
ния a
1
,...,
1 n
xx
2
,...,
1 n
yy
ξ
и a
η
этих случайных величин известны. Необходимо проверить гипотезу
о равенстве дисперсий случайных величин.
1-й шаг. Формирование основной H
0
и альтернативной H
1
гипотез:
22
0
:
ηξ
σ=σH
, .
22
1
:
ηξ
σ≠σH
2-й шаг. Задание уровня значимости α.
3-й шаг. Формирование критической статистики. В качестве меры различия
дисперсий
σ
и выбираем величину ψ
2
ξ
2
η
σ
cr
= .
22
/
ηξ
σσ
Предложение 9.4. Предельное распределение статистики ψ
cr
как случай-
ной величины в случае справедливости гипотезы H
0
стремится к
F−распределению Фишера F(n
1
,
n
2
) с n
1
и n
2
числом степеней свободы
)1,1()(lim
21
,
21
−
−
=
ψ
∞→
nnFxF
кр
nn
. #
4-й шаг. Определение критических границ.
Верхняя критическая граница определяется как процентная точка распре-
деления Фишера уровня α/2: ψ
cr.u
= . Для F−распределения ниж-
няя критическая точка может быть найдена из выражения
),(
21%1002/
nnF
⋅α
ψ
cr.l
= = 1/ψ),(
21%100)2/1(
nnF
⋅α−
cr.u
.
Значение процентной точки
находится из таблиц.
),(
21%1002/
nnF
⋅α
5-й шаг. Расчетное значение критической статистики равно:
117

ψ
calc
=
∑
∑
=
η
=
ξ
η
ξ
−
−
=
σ
σ
2
1
1
2
2
1
2
1
2
2
)(
1
)(
1
n
i
i
n
i
i
ay
n
ax
n
)
)
. (9.7)
Если выполняется условие ψ
cr.l
≤ ψ
calc
≤ ψ
cr.u
, то H
0
верна с ошибкой первого ро-
да α, в противном случае H
0
отвергается.
Пример 9.6. Для данных примера 9.4. проверить, можно ли на уровне зна-
чимости α = 0,01 считать одинаковыми отклонения от среднего времени об-
служивания клиентов банка в первый и второй дни, если известно, что
, ,
8,17][ ==ξ
ξ
mM 6,17][ ==η
η
mM
55
21
=
=
nn .
Решение. Предварительно найдем
14,8,38,8
22
=σ=σ
ηξ
)
)
.
1-й шаг. , .
22
0
:
ηξ
σ=σH
22
1
:
ηξ
σ≠σH
2-й шаг. α = 0,01.
3-й шаг. ψ
cr
= .
22
/
ηξ
σσ
4-й шаг. Находим, используя таблицу процентных точек распределения
Фишера, верхнюю и нижнюю критические границы:
ψ
cr.u
= F
0,5%
(55; 55) = 2,024; ψ
cr.l
= 1/2,024 = 0,494.
5-й шаг. Определяем по (9.8) расчетное значение критической статистики:
ψ
calc
= 8,38/8,14 = 1,03.
Поскольку условие ψ
cr.l
≤ ψ
calc
≤ ψ
cr.u
выполняется, то H
0
принимается.
9.4.2. Проверка гипотез о равенстве дисперсий случайной величины
при неизвестных математических ожиданиях
Пусть имеются две выборки ( ), ( ) случайных величин ξ и
η из нормальных генеральных совокупностей и пусть математические ожида-
ния a
1
,...,
1 n
xx
2
,...,
1 n
yy
ξ
и a
η
этих случайных величин неизвестны. Необходимо проверить гипо-
тезу о равенстве дисперсий случайных величин.
1-й шаг. Формирование гипотез: , .
22
0
:
ηξ
σ=σH
22
1
:
ηξ
σ≠σH
2-й шаг. Задание уровня значимости α.
3-й шаг. Выбор критической статистики ψ
cr
= .
22
/
ηξ
σσ
Предельное распределение статистики
ψ
cr
при неизвестных a
ξ
и a
η
стре-
мится к распределению Фишера:
)1,1()(lim
21
,
21
−
−
=
ψ
∞→
nnFxF
cr
nn
.
4-й шаг. Определение критических границ. Соответственно верхняя и
нижняя критические точки равны:
ψ
cr.u
= , ψ
)1,1(
21%1002/
−−
⋅α
nnF
cr.l
= )1,1(
21%100)2/1(
−
−
⋅α−
nnF = 1/ψ
cr.u
.
5-й шаг. Расчетное значение критической статистики при неизвестных ма-
тематических ожиданиях определяется из выражения
118

ψ
calc
=
∑
∑
=
=
−
−
−
−
=
2
1
1
2
2
1
2
1
2
2
)(
1
1
)(
1
1
n
i
i
n
i
i
y
x
yy
n
xx
n
s
s
. (9.8)
Если выполняется условие ψ
cr.l
≤ ψ
calc
≤ ψ
cr.u
, то H
0
верна с ошибкой первого ро-
да α, в противном случае H
0
отвергается.
Пример 9.7. Для данных примера 9.4 проверить гипотезу о равенстве дис-
персий при неизвестных математических ожиданиях a
ξ
и a
η
для α = 0,1.
Решение. Поскольку a
ξ
и a
η
неизвестны, то определим по исходным дан-
ным их оценки:
84,17==
ξ
xa
)
,
65,17
=
=
η
ya
)
. Далее, используя оценки матема-
тических ожиданий, вычислим несмещенные оценки:
, .
55,8
2
=
x
s 30,8
2
=
y
s
Находим, используя таблицу процентных точек распределения Фишера,
верхнюю и нижнюю критические границы:
ψ
cr.u
= F
5%
(54; 54) = 1,571; ψ
cr.l
= 1/1,571 = 0,637.
Определяем по (9.8) расчетное значение критической статистики:
ψ
calc
= 8,55/8,30 = 1,03.
Поскольку условие ψ
cr.l
≤ ψ
calc
≤ ψ
cr.u
выполняется, то H
0
принимается.
9.4.3. Проверка гипотез о равенстве математических ожиданий слу-
чайных величин при известных дисперсиях
Такая задача ставится обычно тогда, когда выборочные средние оказыва-
ются различными. Возникает вопрос: значимо ли это различие?
Пусть даны две выборки (
), ( ) из нормальных генераль-
ных совокупностей случайных величин ξ и η, и известны их дисперсии. Необ-
ходимо проверить гипотезу о равенстве математических ожиданий.
1
,...,
1 n
xx
2
,...,
1 n
yy
1-й шаг. Формирование гипотез
ηξ
=
aaH :
0
,
ηξ
≠
aaH :
1
.
2-й шаг. Задание уровня значимости α.
3-й шаг. Формирование критической статистики и определение ее закона
распределения при
∞
→∞→
21
, nn : ψ
cr
=
2
2
1
2
// nn
aa
ηξ
ηξ
σ+σ
−
.
Предложение 9.5. Предельное распределение статистики ψ
cr
при извест-
ных
и стремится к нормальному распределению . #
2
ξ
σ
2
η
σ
)1,0()(lim
21
,
NxF
cr
nn
=
ψ
∞→
4-й шаг. Верхняя и нижняя критические точки соответственно равны:
ψ
cr.u
= , ψ
2/1 α−
u
cr.l
= −ψ
cr.u
, где
2/
− квантиль стандартного нормального
распределения уровня 1
− α/2.
1 α−
u
5-й шаг. Определение расчетного значения критической статистики
119
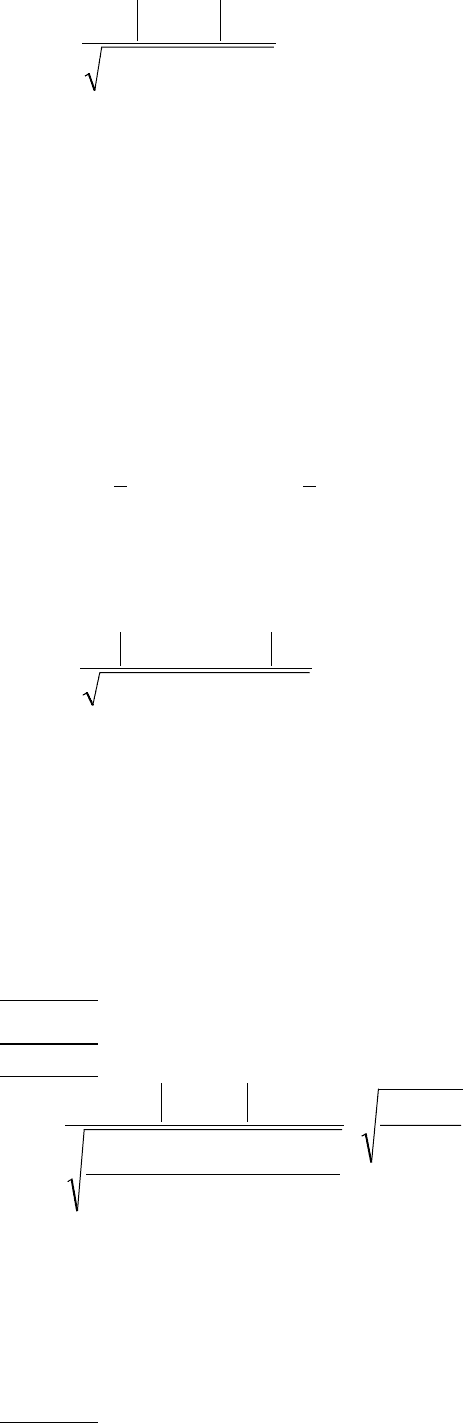
ψ
calc
= .
//
2
2
1
2
nn
aa
ηξ
ηξ
σ+σ
−
)
)
(9.9)
и принятие решения. Если выполняется условие ψ
cr.l
≤ ψ
calc
≤ ψ
cr.u
, то гипотеза
H
0
принимается. В противном случае H
0
отвергается с ошибкой первого рода α.
Замечание 9.7. Данный алгоритм проверки гипотез о равенстве a
ξ
и a
η
можно применять и при отклонении распределения случайных величин ξ и η от
нормального, но при условии, что n
1
и n
2
больше 30.
Пример 9.8. Для данных примера 9.4 проверить для уровня значимости
α
= 0,05 гипотезу о равенстве математических ожиданиях a
ξ
и a
η
при условии,
что дисперсии известны и равны
и .
65,8
2
=σ
ξ
12,8
2
=σ
η
Решение. Оценки математических ожиданий определим по исходным вы-
боркам:
84,17==
ξ
xa
)
,
65,17
=
=
η
ya
)
. Находим, используя таблицу функции
Лапласа, верхнюю и нижнюю критические границы:
ψ
cr.u
=
96,1)475,0(arg
2/05,01
=
Φ
=
−
u
, ψ
cr.l
= −1,96.
Определяем по (9.9) расчетное значение критической статистики:
ψ
calc
=
34,0
55/12,855/65,8
65,1784,17
=
+
−
.
Поскольку условие ψ
cr.l
≤ ψ
calc
≤ ψ
cr.u
выполняется, то H
0
не отвергается.
9.4.4. Проверка гипотез о равенстве математических ожиданий слу-
чайных величин при неизвестных дисперсиях
Пусть имеются две выборки ( ), ( ) из нормальных гене-
ральных совокупностей случайных величин ξ и η. Требуется проверить гипоте-
зу о равенстве a
1
,...,
1 n
xx
2
,...,
1 n
yy
ξ
и a
η
.
1-й шаг. Формирование гипотез
ηξ
=
aaH :
0
,
ηξ
≠
aaH :
1
.
2-й шаг. Задание уровня значимости α.
3-й шаг. Формирование критической статистики
21
21
21
2
2
2
1
2
)1()1(
nn
nn
nn
nn
aa
+
⋅
−+
σ−+σ−
−
ηξ
ηξ
))
ψ
cr
= .
Предложение 9.6. Предельное распределение статистики ψ
cr
стремится к
t−распределению Стьюдента с (n
1
+ n
2
− 2) числом степеней свободы:
)2()(lim
21
,
21
−+
=
ψ
∞→
nntxF
cr
nn
. #
4-й шаг. Верхняя и нижняя критические точки определяются по формулам:
ψ
cr.u
= t , ψ)2(
21%1002/
−+
⋅α
nn
cr.l
= −ψ
cr.u
,
120
