Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие

Подождите немного. Документ загружается.

8.3. Интервальные оценки числовых характеристик случайных

величин

Точечные оценки параметров генеральной совокупности могут быть при-

няты в качестве ориентировочных, первоначальных результатов обработки вы-

борочных данных. Их недостаток заключается в том, что неизвестно, с какой

точностью оценивается параметр. Если для выборок большого объема точность

обычно бывает достаточной (при условии несмещенности, эффективности и со-

стоятельности оценок), то для выборок

небольшого объема вопрос точности

оценок становится очень важным.

Определение 8.4. Интервальной оценкой параметра θ называется числовой

интервал

(

)

)2()1(

θθ

)

, который с заданной вероятностью γ накрывает неизвестное

значение параметра θ (рис.8.1):

γ=θθ∈θ=θ<θ<θ },({)(

)2()1()2()1(

nnnn

)

Рис. 8.1.

Границы интервала ),(

)2()1(

θθ

)

и его величина находятся по выборочным

данным, т.е. являются случайными величинами в отличие от параметра θ − ве-

личины неслучайной. Поэтому правильнее говорить о том, что интервал

),(

)2()1(

θθ

)

«накрывает», а не «содержит» значение θ. Числа

)1(

)

)2(

)

называ-

ются доверительными границами, интервал ),(

)2()1(

θθ

)

− доверительным интер-

валом для параметра θ. Число γ называется доверительной вероятностью (или

надежностью сделанной оценки).

Сначала задается надежность. Обычно ее выбирают равной 0,95, 0,99 или

0,999. Тогда вероятность того, что интересующий нас параметр попал в интер-

вал ),(

)2()1(

θθ

)

достаточно высока. Число 2/)(

)2()1(

θ+θ

)

– середина доверитель-

ного интервала – будет давать значение параметра θ с точностью

2/)(

)1()2(

θ−θ

)

. Доверительный интервал ),(

)2()1(

θθ

)

может накрывать параметр θ

или нет. Именно в таком смысле нужно понимать случайное событие, заклю-

чающееся в том, что доверительный интервал накрывает число θ. Величина до-

верительного интервала существенно зависит от объема выборки n (уменьша-

ется с ростом n) и от значения доверительной вероятности γ (увеличивается с

приближением γ к 1).

Очень часто (но не всегда) доверительный интервал вы-

бирается симметричным относительно параметра θ. Наибольшее отклонение ∆

оценки

)

от истинного значения параметра θ, которое возможно с заданной

доверительной вероятностью γ, называется предельной ошибкой выборки.

101

8.3.1. Доверительный интервал для математического ожидания нор-

мального распределения при известной дисперсии

Пусть случайная величина ξ (можно говорить о генеральной совокупности)

распределена по нормальному закону, для которого известна дисперсия

. Из генеральной совокупности делается случайная выборка X

][ σ=ξD

, … , X

объема n, которая рассматривается как совокупность n независимых случайных

величин, распределенных так же как ξ. Ранее также обсуждались равенства:

][][...][],[][...][

XDXDXDXMXMXM

=== ,

XDXMXM

][

][],[][ == .

Случайная величина

также распределена по нормальному закону (см.

предложение 4.7). Обозначим неизвестную величину M[ξ] через a и подберем

по заданной надежности γ число d > 0 так, чтобы выполнялось условие

(

)

γ=<− daXP . (8.8)

Так как

распределена по нормальному закону N(a, σ

/n), то получаем

(

)

=+<<−=<− )( daXdaPdaXP

⎟

⎠

⎞

⎜

⎝

⎛

Φ=

⎟

⎠

⎞

⎜

⎝

⎛

−−

Φ−

⎟

⎠

⎞

⎜

⎝

⎛

−+

ada

Осталось подобрать d таким, чтобы выполнялось равенство

γ=

⎟

⎠

⎞

⎜

⎝

⎛

2 или

⎟

⎠

⎞

⎜

⎝

⎛

. Для любого

]1,0[∈

можно по таблице найти такое число (кван-

тиль) t, что

2)(

=Φ t . Теперь из равенства

определим

Окончательный результат получим, представив формулу (8.8) в виде:

γ=

⎟

⎠

⎞

⎜

⎝

⎛

+<<

−

Смысл последней формулы состоит в следующем: с надежностью γ довери-

тельный интервал

⎟

⎠

⎞

⎜

⎝

⎛

−

X ;

покрывает неизвестный параметр a = M[ξ]

генеральной совокупности. Можно сказать иначе: точечная оценка

опреде-

ляет значение параметра M[ξ] с точностью

ntd σ=

и надежностью γ.

Пример 8.7. Пусть имеется генеральная совокупность с некоторой харак-

теристикой, распределенной по нормальному закону с дисперсией, равной 6,25.

Произведена выборка объема n = 27 и получена выборочная средняя арифмети-

ческая

12=

. Найти доверительный интервал, покрывающий неизвестное ма-

тематическое ожидание исследуемой характеристики генеральной совокупно-

сти с надежностью γ = 0,99.

102

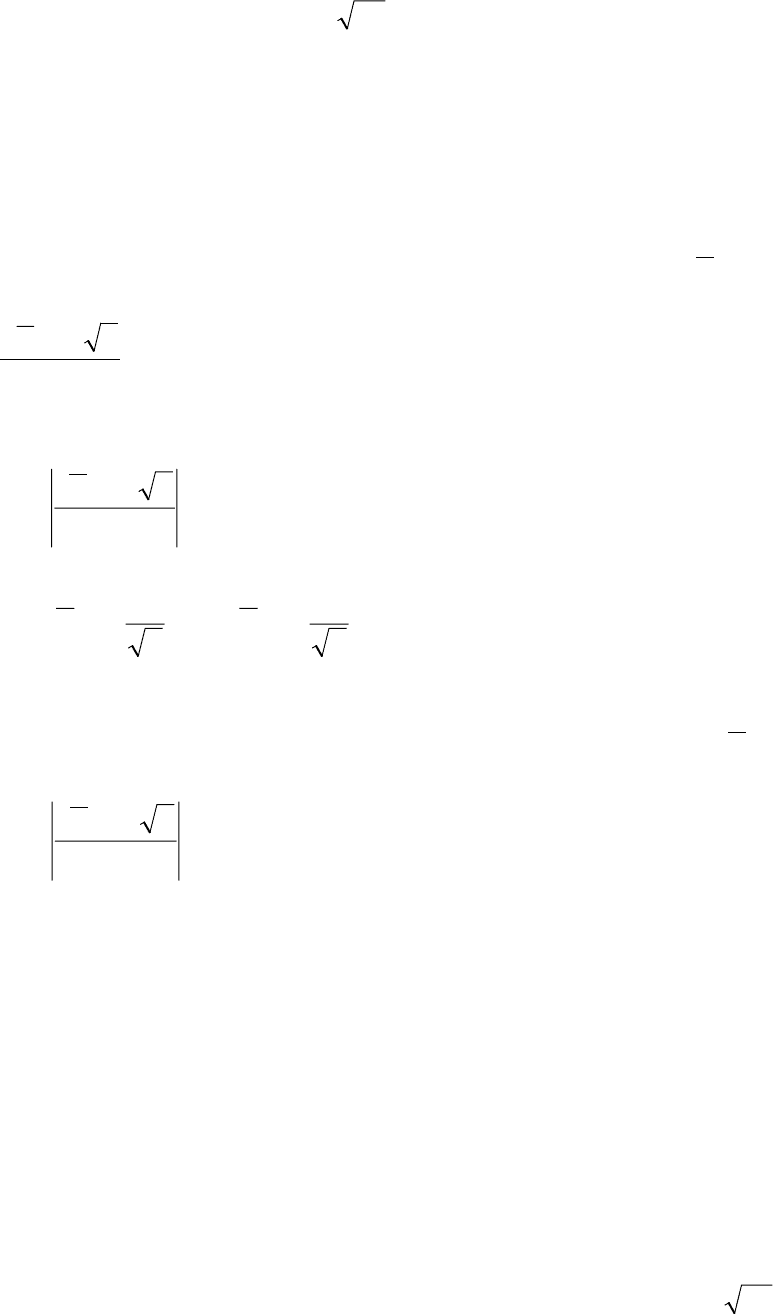
Решение. Сначала по таблице для функции Лапласа найдем значение t из

равенства

495,02/)( =

=Φ

. По полученному значению t = 2,58 определим

точность оценки

24,127/58,25,2 ≈⋅=d

. Отсюда получаем искомый довери-

тельный интервал: (10,76; 13,24).

8.3.2. Доверительный интервал для математического ожидания нор-

мального распределения при неизвестной дисперсии

Пусть ξ – случайная величина, распределенная по нормальному закону с

неизвестным математическим ожиданием M[ξ], которое обозначим a. Произве-

дем выборку объема n. Определим среднюю выборочную

и несмещенную

выборочную дисперсию s

по известным формулам. Случайная величина

naX

)( −

= распределена по закону Стьюдента с (n – 1) степенями свободы.

Задача заключается в том, чтобы по заданной надежности γ и по числу

степеней свободы (n – 1) найти такое число t

, чтобы выполнялось равенство

()

γ=

⎟

⎠

⎞

⎜

⎝

⎛

−

naX

(8.9)

или эквивалентное равенство

γ=

⎟

⎠

⎞

⎜

⎝

⎛

+<<−

γγ

tXa

tXP

. (8.10)

Здесь в скобках написано условие того, что значение параметра a принадлежит

некоторому промежутку, который и является доверительным интервалом, гра-

ницы которого зависят от надежности γ и параметров выборки

и s.

Чтобы определить значение t

по величине γ, преобразуем(8.9) к виду

()

γ−=

⎟

⎠

⎞

⎜

⎝

⎛

≥

−

naX

P .

Теперь по таблице процентных точек для случайной величины t, распределен-

ной по закону Стьюдента, по вероятности (1 – γ)/2 и числу степеней свободы

(n − 1) находим t

(1−γ)/2%

. Формула (8.10) дает ответ поставленной задачи.

Пример 8.8. На контрольных испытаниях 20-ти электроламп средняя про-

должительность их работы оказалась равной 2000 часов при среднем квадрати-

ческом отклонении, равном 11-ти часам. Известно, что продолжительность ра-

боты лампы является нормально распределенной случайной величиной. Опре-

делить с надежностью 0,95 доверительный интервал для математического ожи-

дания этой случайной величины.

Решение. Величина (1 – γ)/2 в данном

случае равна 0,025. По таблице рас-

пределения Стьюдента, при числе степеней свободы, равном 19, находим:

(1−γ)/2%

= 2,093. Вычислим теперь точность оценки:

148,520/11093,2 =⋅

. От-

сюда получаем доверительный интервал: (1994,852; 2005,148).

103

8.3.3. Доверительный интервал для дисперсии нормального распреде-

ления

Пусть случайная величина ξ распределена по нормальному закону с неиз-

вестной дисперсией D[ξ]. Делается выборка объема n. Из нее определяется не-

смещенная выборочная дисперсия s

. Случайная величина

()

][

sn −

=χ рас-

пределена по закону χ

c (n – 1) степенями свободы. По заданной надежности γ

можно найти сколько угодно границ

и интервалов, таких что

γ=χ<χ<χ )(

P . (8.11)

Найдем

и из следующих условий:

)(

−

=χ≤χP

)(

−

=χ≥χP

. (8.12)

Очевидно, что при выполнении условий (8.12) справедливо равенство (8.11).

В таблицах для случайной величины χ

обычно дается решение уравнения

. Из такой таблицы по заданной величине q и по числу степеней

свободы (n – 1) можно определить значение . Таким образом, сразу находит-

ся значение

в формуле (8.12). Для определения преобразуем (8.12):

=χ≥χ )(

1)(

γ+

γ−

−=χ≥χP

Полученное равенство позволяет определить по таблице значение

Теперь, найдя значения

и , представим равенство (8.11) в виде

γ=

⎟

⎠

⎞

⎜

⎝

⎛

χ<

−

<χ

][

)1(

P .

Последнее равенство перепишем в такой форме, чтобы были определены гра-

ницы доверительного интервала для неизвестной величины D[X]:

γ=

⎟

⎠

⎞

⎜

⎝

⎛

−

)1(

][

)1( sn

P .

Отсюда доверительный интервал для стандартного отклонения равен

γ=

⎟

⎠

⎞

⎜

⎝

⎛

−

)1(

][

)1( sn

. (8.13)

Пример 8.9. Считаем, что шум в кабинах вертолетов одного и того же ти-

па при работающих в определенном режиме двигателях – случайная величина,

распределенная по нормальному закону. Было случайным образом выбрано 20

вертолетов, и произведены замеры уровня шума (в децибелах) в каждом из

них. Несмещенная выборочная дисперсия измерений оказалась равной 22,5.

104

Найти доверительный интервал, накрывающий неизвестное стандартное откло-

нение величины шума в кабинах вертолетов данного типа с надежностью 98%.

Решение. По числу степеней свободы, равному 19, и по вероятности

находим из таблицы процентных точек распределения χ

01,02/)98,01( =−

ве-

личину

. Аналогичным образом для вероятности

получаем . Используем формулу (8.13):

191,36)19(

=χ=χ

99,02/)98,01( =+

633,7)19(

%99

=χ=χ

437,3

191,36

5,2219

)1(

⋅

− sn

484,7

633,7

5,2219

)1(

⋅

− sn

Отсюда искомый доверительный интервал составляет (3,437; 7,484).

Глава 9. Проверка статистических гипотез

На практике часто приходится на основе выборочных наблюдений прове-

рять различные предположения относительно генеральной совокупности. Про-

цедуру сопоставления выдвинутых гипотез с выборкой и решения вопроса от-

носительно приемлемости этих гипотез называют проверкой гипотез.

9.1. Статистическая гипотеза и общая схема ее проверки

Определение 9.1. Статистической гипотезой называется любое предпо-

ложение о виде или параметрах неизвестного закона распределения.

Примеры статистических гипотез: нормально распределенная случайная

величина ξ имеет генеральную среднюю, равную a; нормально распределенная

случайная величина ξ имеет дисперсию, равную σ

; выборка (x

, … , x

) взята из

нормально распределенной генеральной совокупности.

Проверяемую гипотезу обычно называют основной (или нулевой) и обозна-

чают H

. Наряду с нулевой гипотезой H

рассматривают альтернативную гипо-

тезу H

, являющуюся логическим дополнением H

. Нулевая и альтернативная

гипотезы представляют собой две возможности выбора, осуществляемого в за-

дачах проверки статистических гипотез. Правило, по которому гипотеза H

от-

вергается или принимается, называется

статистическим критерием.

Определение 9.2. Процедура обоснованного сопоставления высказанной

гипотезы с выборкой (x

, … , x

), осуществляемая с помощью того или иного

статистического критерия, называется статистической проверкой гипотезы.

Результат такого сопоставления может быть как отрицательным (наблюде-

ния противоречат выдвинутой гипотезе, следовательно, от нее надо отказаться),

так и положительным (наблюдения не противоречат высказанной гипотезе, и ее

можно принять в качестве одного из решений). Неотрицательный результат

проверки гипотез

не означает, что высказанное нами предположительное ут-

105

верждение является наилучшим. Могут также существовать другие гипотезы,

которые не будут противоречить тем же эмпирическим данным.

Статистические критерии проверки гипотез разнообразны, но у них единая

логическая схема построения критерия, которая укладывается в 5 этапов.

Этап 1. Выдвигается основная гипотеза H

Этап 2. Задается уровень значимости критерия α. Любое статистическое

решение, принимаемое на основе ограниченного ряда наблюдений, сопровож-

дается, хоть и малой, вероятностью ошибочного заключения. Именно в доле

случаев α гипотеза H

может быть отвергнута при условии, что она верна. Та-

кие ошибки называют ошибками 1-го рода.

Или, наоборот, в доле случаев β мы можем принять гипотезу H

, в то время

как она ошибочна. Эти ошибки являются ошибками 2-го рода.

При фиксированном объеме выборки n величины вероятностей α или β мы

можем выбирать самостоятельно. Если есть возможность сколь угодно увели-

чивать n, то теоретически можно добиться как угодно малых ошибок α и β при

любой фиксированной альтернативной гипотезе H

Определение 9.3. Вероятность α допустить ошибку 1-го рода, т.е. отверг-

нуть гипотезу H

, когда она верна, называется уровнем значимости критерия и

определяется как α = P(H

Чем весомее для исследователя потери от ошибочного непринятия гипоте-

зы H

, тем меньшее α необходимо выбирать. Обычно пользуются стандартны-

ми значениями α (0,1; 0,05; 0,025; 0,01; 0,005; 0,001).

Пример 9.1. Величина α = 0,05 означает, что в среднем в 5 случаях из 100

при использовании данного статистического критерия будет ошибочно отвер-

гаться справедливая основная гипотеза H

Этап 3. Задается некоторая функция результатов наблюдения – критиче-

ская статистика (critical statistics)

= ψ(x

, … , x

), (9.1)

которая также является случайной величиной и в предположении справедливо-

сти H

подчинена некоторому хорошо изученному (затабулированному) закону

распределения с плотностью вероятности

)(xp

Замечание 9.1. Содержательный смысл критической статистики – мера

расхождения имеющейся в распоряжении исследователя выборки с основной

гипотезой

. Например, в гипотезе об однородности двух выборок случайных

величин ξ и η критическая статистика ψ

суть мера различия между функциями

распределения F

(x) и F

(x).

Определение 9.4. Статистикой называется любая (измеримая) функция

θ = θ(x

, … , x

) от выборки данных.

106

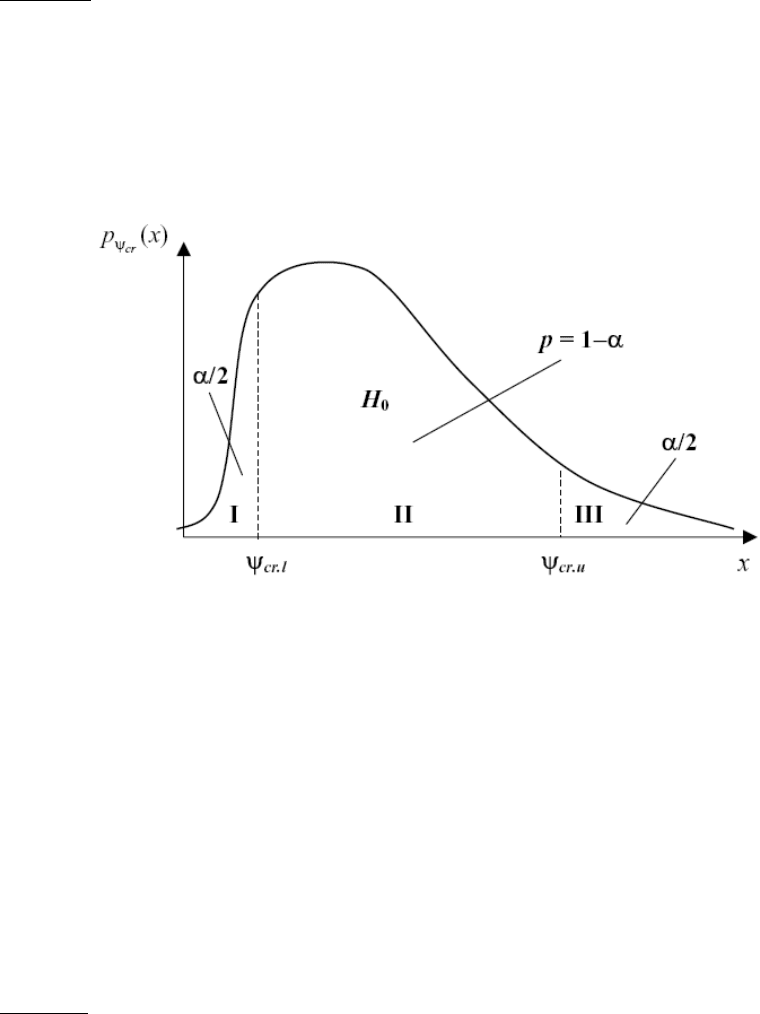
Этап 4. Из статистических таблиц распределения находятся про-

центные точки (1 – α/2)⋅100% и α/2⋅100% –

)(xp

%100)2/1( ⋅α−

и , являющиеся

соответственно нижней (lower) ψ

%1002/ ⋅α

cr.l

и верхней (upper) ψ

cr.u

критическими точка-

ми (границами). Они делят всю область допустимых значений ψ

на области

(рис. 9.1): неправдоподобно малых (I); правдоподобных (II); неправдоподобно

больших (III).

Рис. 9.1. График плотности вероятности критической статистики с выделением

областей принятия и непринятия гипотезы H

Область принятия гипотезы H

определяется как доверительный интервал

для ψ

, который формируется на основе закона распределения статистики ψ

при уровне доверительной вероятности p = 1 – α.

Различают односторонние и двухсторонние критерии. Для односторонне-

го критерия область принятия гипотезы H

может иметь ограничение только с

одной стороны (сверху или снизу). При этом область значений статистики ψ

разбивается на две: область правдоподобных и область неправдоподобно боль-

ших или неправдоподобно малых значений. Для двухстороннего критерия об-

ласть принятия гипотезы H

имеет два ограничения – сверху и снизу.

Этап 5. Определяется расчетное (calculation) значение критической стати-

стики ψ

calc

подстановкой в (9.1) конкретных выборочных значений (x

, … , x

)

или некоторых функций от них. Если окажется, что ψ

calc

принадлежит области

правдоподобных значений, то гипотеза H

верна, т. е. не противоречит выбо-

рочным данным. В противном случае H

отвергается с ошибкой 1-го рода α.

Отвержение H

означает, что ψ

calc

не подчиняется закону распределения

. Ошибка 2-го рода возникает, если принимается H

)(xp

, в то время когда

она неверна. Ее вероятность β равна β = P(H

Вероятность (1 – β) не допустить ошибку 2-го рода, т.е. отвергнуть гипоте-

зу H

, когда она неверна, называется мощностью критерия.

Замечание 9.2. Очевидно, что из двух критериев, характеризующихся оди-

наковой вероятностью α отвергнуть в действительности правильную гипотезу

107

108

, следует предпочесть тот, который сопровождается меньшей ошибкой 2-го

рода (или большей мощностью).

Принятие гипотезы H

в сравнении с альтернативной H

не означает, что

мы уверены в абсолютной правильности H

или, что высказанное в гипотезе H

утверждение является наилучшим, единственно подходящим. Просто гипотеза

не противоречит имеющимся у нас выборочным данным. Таким же свойст-

вом, наряду с H

, могут обладать и другие гипотезы. Более того, возможно, что

при увеличении объема выборки n либо при испытании H

против другой аль-

тернативной гипотезы H

гипотеза H

будет отвергнута. Так что принятие ги-

потезы H

следует расценивать не как раз и навсегда установленный, абсо-

лютно верный содержащийся в ней факт, а лишь как достаточно правдопо-

добное, не противоречащее опыту утверждение.

По прикладному содержанию статистические гипотезы можно разделить

на следующие типы: о типе законе распределения исследуемой случайной ве-

личины; об однородности выборок; о числовых характеристик случайных

вели-

чин; о стохастической независимости элементов выборки; об общем виде моде-

ли, описывающей статистическую зависимость между признаками.

Ниже рассмотрим основные гипотезы из первых четырех типов. Последняя

группа статистических гипотез об общем виде модели статистической зависи-

мости между признаками рассматривается в разделе 3.

9.2. Критерии согласия

Критерии согласия предназначены для статистической проверки гипотез о

соответствии эмпирического распределения выборки данных выбранной моде-

ли теоретического закона распределения.

Пусть выдвинута гипотеза о том, что случайная выборка из генеральной

совокупности может быть описана некоторой моделью с функцией распределе-

ния F

mod

(x, Θ), где Θ = (θ

, … , θ

) − вектор параметров, которые могут быть как

известны, так и неизвестны.

Большинство критериев проверки согласия основаны на использовании

меры расстояний между анализируемой эмпирической функцией распределе-

ния F

(x), определенной по выборке объема n, и модельной F

mod

(x, Θ).

9.2.1. Критерий согласия χ

−Пирсона

Критерий согласия χ

−

Пирсона позволяет осуществлять проверку гипоте-

зы о согласии, когда параметры модели неизвестны. Неизвестные параметры

модели могут быть заменены в модели их оценками, полученными по выборке,

одним из точечных методов оценивания (см. § 8.1). Критерий согласия

−Пирсона требует, чтобы:

- количество n

, (i = 1, … , L) попаданий в каждый интервал должно быть не

менее 4. В противном случае соседние интервалы необходимо объединить в

один, не забывая при этом корректировать L;

- выборка должна быть сгруппирована, а ее объем не слишком мал.

Рассмотрим последовательность критерия согласия χ

−Пирсона.

1-й шаг. Формирование основной и альтернативной гипотез

),()(:

mod0

Θ= xFxFH

),()(:

mod1

≠

xFxFH

. (9.2)

2-й шаг. Задание уровня значимости α.

3-й шаг. Формирование критической статистики ψ

∑

−

npn

)(

, где

= F

mod

i+1

, Θ) − F

mod

, Θ) − теоретическая вероятность попадания в i-й ин-

тервал

. Предельное распределение ψ

],[

1+ii

при

∞

→n

имеет вид

)1(

)(

lim

−−χ=

−

∑

∞→

npn

где S − количество параметров модельного распределения, согласие с которым

проверяется, χ

(L − S − 1) − функция χ

−распределения с (L − S − 1) числом сте-

пеней свободы.

4-й шаг. Определение верхней и нижней критических точек по таблице

процентных точек χ

−распределения:

cr.u

= , ψ

)1(

%1002/

−−χ

⋅α

cr.l

= .

)1(

%100)2/1(

−−χ

⋅α−

5-й шаг. Определение расчетного значения критической статистики

∑

−

npn

)(

calc

. (9.3)

Если выполняется условие ψ

cr.l

≤ ψ

calc

≤ ψ

cr.u

, то гипотеза о согласии H

верна с ошибкой первого рода α. В противном случае гипотеза H

отвергается.

Отвержение гипотезы H

в случае слишком маленьких значений критической

статистики, т.е. при ψ

calc

< ψ

cr.l

, на первый взгляд противоречит здравому смыс-

лу. Однако надо отметить, что ψ

calc

как статистика также является случайной

величиной со своей дисперсией. А значит одинаково неправдоподобными мож-

но считать как слишком большие, так и слишком малые ψ

calc

Причинами возникновения слишком малых ψ

calc

могут быть как неудачный

выбор F

mod

(x, Θ) (например, при искусственном завышении числа параметров

модели или ошибочной модели), так и некорректное проведение эксперимента

при деформировании выборки (например, стремление искусственно «подог-

нать» эмпирические данные под результат).

Замечание 9.3. Использование критерия основано на теореме Пирсона–

Фишера, которая утверждает, что если гипотеза H

истинна, то при некоторых

достаточно общих условиях распределение статистики ψ

calc

, определяемой по

формуле (9.3), сходится (при n → ∝) к χ

(L − S − 1)−распределению.

Замечание 9.4. Критерий согласия χ

−Пирсона достаточно эффективен, ко-

гда все ожидаемые частоты np

≥ 10, (i = 1, … , L).

109

Пример 9.2. Проверить с помощью критерия χ

−Пирсона согласованность

эмпирического распределения рабочих по выработке (таблица 9.1), с нормаль-

ным законом на уровне значимости α = 0,05.

Таблица 9.1

№№

Выработка в от-

четном году в % к

предыдущему, x

Количество ра-

бочих, n

1 94 – 100 3

2 100 – 106 7

3 106 – 112 11

4 112 – 118 20

5 118 – 124 28

6 124 – 130 19

7 130 – 136 10

8 136 – 142 2

Всего 100

Решение. Параметры нормального закона – математическое ожидание a и

дисперсия σ

неизвестны, поэтому заменяем их на выборочную среднюю

выборочную дисперсию

)

(т.к. число наблюдений n = 100 достаточно велико),

равные

2,119=

и 42,8735,9

==σ

)

Для расчета вероятностей p

попадания случайной величины ξ в интервал

используем функцию Лапласа:

],[

1+ii

≈

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

Φ−

⎟

⎠

⎞

⎜

⎝

⎛

−

Φ=≤ξ≤

axax

xxp

iii

)(

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

Φ−

⎟

⎠

⎞

⎜

⎝

⎛

−

35,9

2,119

35,9

2,119

1 ii

Например,

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

Φ−

⎟

⎠

⎞

⎜

⎝

⎛

−

Φ=≤ξ≤

35,9

2,11994

35,9

2,119100

)10094(

[]

0166,0)9928,09596,0(5,0)69,2()05,2(5,0

−

Φ−−Φ=

, и соответствующая

первому интервалу теоретическая частота

7,10166,0100

≈

⋅

и т.д.

Для определения статистики ψ

calc

удобно составить таблицу 9.2.

Учитывая, что в рассматриваемом эмпирическом распределении частоты

первого и последнего интервалов (n

= 3, n

= 1) меньше 4, объединим эти ин-

тервалы с соседними (см. табл. 9.2). Итак, расчетное значение статистики

calc

= 2,27. Т.к. новое число интервалов (с учетом объединения крайних) L = 6,

а нормальный закон распределения определяется S = 2 параметрами, то число

степеней свободы k = L − S − 1 = 6 − 2 − 1 = 3. Верхнее и нижнее критические

значения статистики определим из статистической таблицы процентных точек:

cr.u

35,9)3()3(

%5,2

%100

05,0

=χ=χ

⋅

, ψ

cr.l

22,0)3()3(

%5,97

%100)

05,0

=χ=χ

⋅−

Т.к. ψ

cr.l

≤ ψ

calc

≤ ψ

cr.u

, то гипотеза о выбранном теоретическом нормальном

законе N(119,2; 87,42) согласуется с опытными данными.

110