Турчина Н.В. Физика в задачах для поступающих в вузы

Подождите немного. Документ загружается.

180

Полученную воду довели до ипения и ипятили до тех пор, поа

не испарилась ее четвертая часть. Время все8о процесса τ =40мин.

Определите КПД плити.

9.2.5. Ти8ель с оловом на8ревают элетричесим тоом. Ко-

личество теплоты, ежесеундно подводимое  ти8лю, постоянно.

За время τ

= 10 мин олово на8релось от температуры t

=20°C до

=70°C и спустя еще τ

= 83 мин полностью расплавилось. Най-

дите удельную теплоту плавления олова.

9.2.6. Коньобежец массой m = 55 8, имеющий начальную

сорость v = 8,5 м/с, сользит по льду и останавливается. Лед нахо-

дится при температуре t =0°C. Каая масса льда растает, если

η = 50% оличества теплоты, выделенной в результате трения, по-

8лощается льдом?

9.2.7. На сольо энер8ия молеулы воды при температуре 0 °C

больше энер8ии молеулы льда при температуре 0 °C?

9.2.8. С аой наименьшей высоты должна упасть льдина,

чтобы при ударе о землю она растаяла? Начальная температура

льдини t =0°C. Сопротивление воздуха не учитывать. Считать,

что вся энер8ия идет на плавление льдини.

9.2.9. При аой сорости свинцовая пуля, ударившись о пре-

8раду, плавится? Температура пули до удара t = 100 °C. При ударе

η = 60% энер8ии пули превращается во внутреннюю.

9.2.10. При выстреле вертиально вверх свинцовая пуля удари-

лась о неупру8ую пре8раду и расплавилась. На аой высоте про-

изошло это столновение, если начальная сорость пули v

= 350 м/с,

а на на8ревание и плавление пули ушло η = 50% выделивше8ося о-

личества теплоты? Температура пули в момент соударения t

=100°C. Сопротивление воздуха не учитывать.

9.2.11. С аой минимальной соростью относительно поверх-

ности осмичесо8о орабля должен дви8аться небольшой желез-

ный метеорит, чтобы расплавиться в результате удара? Считать,

что удар абсолютно неупру8ий и до столновения температура ме-

теорита T

= 100 К, а на плавление и на8ревание идет η = 25% вы-

делившейся при ударе энер8ии.

9.2.12. Два одинаовых усоча льда летят навстречу дру8 дру8у

с равными соростями и при ударе обращаются в воду. Оцените мини-

мально возможные сорости льдино перед ударом, если они имели

одинаовую температуру t

=–12°C до удара и t

=80°C после удара.

 9.2.13. С аой минимальной соростью свинцовая пуля

должна ударить в подвижный эран, чтобы расплавиться? Счи-

тать, что удар абсолютно неупру8ий и на на8рев и плавление пу-

ли идет η =60% энер8ии неупру8ой деформации. Масса пули

m = 10 8. Масса эрана M = 1 8. К моменту удара температура

пули t = 100 °C.

181

9.3. Парообразование

9.3.1. Ртуть массой m = 1 8 при температуре ипения обраща-

ют в пар той же температуры. На сольо изменилась внутренняя

энер8ия ртути?

9.3.2. Каое оличество теплоты потребуется, чтобы 100 8 во-

ды, взятой при 10 °C, на8реть до 100 °C и обратить в пар?

9.3.3. Каое минимальное оличество теплоты надо сообщить

льду массой m = 2 8, взятому при температуре t

=–10°C, чтобы

превратить е8о в пар при температуре t

=100°C?

 9.3.4. В элетричесий чайни мощностью N = 1 Вт налива-

ют V = 2 л воды при температуре t =18°C и влючают в сеть. Че-

рез аое время вся вода испарится? КПД на8ревателя η =50%.

Удельная теплоемость воды c = 4,2 Дж/(8 · К), удельная тепло-

та парообразования воды r = 2,26 МДж/8, плотность воды ρ =

=10

8/м

9.3.5. Кусо льда при температуре t =–10°C положили в эле-

трочайни и стали е8о на8ревать. Спустя время τ = 30 мин из чай-

ниа испарилась десятая часть воды. Мощность чайниа N =1Вт.

КПД плити η = 40%. Найдите массу уса льда.

9.3.6. При на8ревании неоторой массы воды от температуры

=0°C до температуры ипения t



=100°C на элетричесом на-

8ревателе понадобилось τ

= 15 мин. После это8о потребовалось

= 80 мин для превращения этой воды в пар. Определите удель-

ную теплоту парообразования.

9.3.7. Чайни, в оторый налили воду при температуре

=10°C, поставили на элетроплиту. Через τ

= 10 мин вода за-

ипела. Через аое время вода полностью выипит?

9.3.8. Каое оличество теплоты потребуется для суши све-

жих фрутов массой m = 10 т, если масса 8отовой продуции со-

ставляет η = 20% от массы свежих фрутов, начальная температу-

ра фрутов 20 °C, температура в сушиле 80 °C, а удельная теплота

парообразования равна 2,3 · 10

Дж/8?

9.3.9. В дьюаровсом сосуде хранится жидий азот при темпера-

туре T

=78К объемом V = 2 л. За сути испарилась половина азота.

Определите удельную теплоту испарения азота, если известно, что лед

массой m =40 8 в том же сосуде растает в течение τ

= 22 ч 30 мин.

Количество теплоты, ежесеундно получаемое сосудом, пропорцио-

нально разности температур внутри и снаружи сосуда. Температура

оружающе8о воздуха T = 293 К. Плотность жидо8о азота при

78 К равна ρ = 800 8/м

9.3.10. На сольо больше энер8ия молеулы пара воды при тем-

пературе 100 °C, чем энер8ия молеулы воды при той же температуре?

182

9.3.11. С аой наименьшей высоты должна падать дождевая

апля, чтобы при ударе о землю она испарилась? Начальная темпе-

ратура апли t

=20°C. Сопротивление воздуха не учитывать.

9.3.12. С аой минимальной соростью влетает метеорит в ат-

мосферу Земли, если он при этом на8ревается, плавится и превра-

щается в пар? Метеоритное вещество состоит из железа, и е8о на-

чальная температура T = 100К. Считать, что на на8ревание мете-

орита идет η = 20% от е8о механичесой энер8ии.

9.4. Удельная теплота с#орания топлива

9.4.1. Масса пороха в аждом патроне пулемета m = 3,2 8. Ка-

ое оличество теплоты выделится за N = 10 выстрелов?

9.4.2. На сольо 8радусов можно на8реть воду объемом V =100л

при сжи8ании древесно8о у8ля массой m = 0,5 8, если бы все оличе-

ство теплоты, выделяемое при с8орании, пошло на на8ревание воды?

9.4.3. Найдите оэффициент полезно8о действия примуса, в

отором при на8ревании воды массой m

= 3 8 от температуры

=20°C до температуры t

=80°C с8орело m

= 50 8 бензина.

9.4.4. Каую массу меди можно расплавить в плавильной печи

с КПД η = 30%, сжи8ая ос массой m = 2 т, если начальная тем-

пература меди t =20°C?

9.4.5. Каую массу еросина нужно сжечь в примусе с КПД

η = 40%, чтобы расплавить m = 4 8 льда, взято8о при темпера-

туре –10 °C, если удельная теплота с8орания еросина q =

=42000Дж/8?

9.4.6. Пуля массой М = 9 8 вылетает из ствола винтови со со-

ростью v = 900 м/ с. Определите КПД выстрела, если масса порохо-

во8о заряда m = 4 8.

9.4.7. Заряд 305-миллиметровой пуши содержит m =1558

пороха. Масса снаряда М = 446 8. Каова масимальная даль-

ность полета снаряда, если КПД орудия η =28%?

9.4.8. При сорости движения v = 72 м/ч судно развивает

мощность N = 1500 Вт. КПД дви8ателя судна η = 30%. Найдите

расход топлива на один илометр пути при таом движении.

Удельная теплота с8орания топлива q = 50 МДж/8.

9.4.9. На сольо илометров пути хватит одной заправи авто-

мобиля (объем баа V = 40 л) при постоянной сорости движения

v = 60 м/ч, если КПД дви8ателя η = 50%, а мощность автомобиля

N =40Вт?

9.4.10. Реативный самолет пролетает с постоянной соростью

v = 900 м/ч расстояние l = 1800 м. При этом он расходует топли-

во массой m = 4 т. Мощность дви8ателя самолета N=5900Вт,

183

КПД дви8ателя η = 23%. Найдите удельную теплоту с8орания топ-

лива, применяемо8о на самолете.

9.4.11. Каое оличество природно8о 8аза надо сжечь, чтобы

m = 4 8 льда, взято8о при температуре t

=–20°C, превратить в

пар с температурой t

= 100 °C? КПД на8ревателя η =60%.

9.4.12. При с8орании m = 1 8 водорода и превращении е8о в во-

ду выделяется оличество теплоты Q= 142 Дж. Каую массу а-

менно8о у8ля надо сжечь для диссоциации V = 1 л воды, если из вы-

деляемой у8лем энер8ии используется η =50%?

9.4.13. Реативный самолет имеет четыре дви8ателя, разви-

вающих силу тя8и F = 20 104 Н аждый. Каую массу еросина из-

расходует самолет на перелет протяженностью s = 500 м? КПД

дви8ателя η =25%.

9.4.14. На сольо увеличится расход бензина на пути s =1м

при движении автомобиля массой m =10

8 по доро8е с подъемом

h = 3 м на аждые l = 100 м пути по сравнению с расходом бензина

по 8оризонтальной доро8е? КПД дви8ателя η = 30%. Сорость в обо-

их случаях одинаова.

9.5. Уравнение теплово#о баланса

9.5.1. В чу8унный сосуд массой m

= 2 8, температура оторо-

8о t

=10°C, налили воду объемом V = 5 л. Найдите установившую-

ся температуру, если начальная температура воды t

= 100 °C.

9.5.2. В воду объемом V

=150см

при температуре t

=40°C влили

воду объемом V

=250см

при t

=20°C. Найдите температуру смеси.

9.5.3. В стелянную чашу массой m = 300 8 с температурой

=25°C наливают V =200см

чая, имеюще8о температуру t

= 95 °C.

Каая температура будет у чаши с чаем после установления тепло-

во8о равновесия? Теплообменом с оружающей средой пренебречь.

9.5.4. Смешано V

= 24 л воды при температуре t

=12°C и

=40л воды при t

=80°C. Определите установившуюся температу-

ру, если во время смешивания было «потеряно» оличество теплоты

Q =420Дж.

9.5.5. В воду массой m

= 5 8 при температуре T

=353К до-

бавили m

= 2 8 холодной воды. При этом начальная температура

на8ретой воды снизилась на n = 5%. Определите начальную темпе-

ратуру холодной воды.

9.5.6. В аом отношении следует смешать две массы воды,

взятые при температурах t

=55°C и t

=0°C, чтобы температура

смеси стала равной θ =21°C?

9.5.7. В алориметр налили V = 1 л воды при температуре

=27°C. Затем в воду опустили металличесий брусо массой

184

m = 0,25 8, на8ретый до температуры t

=127°C. В результате

температура воды поднялась до t =34°C. Определите удельную

теплоемость металла. Теплоемость алориметра не учитывать.

9.5.8. Чему будет равна температура в состоянии теплово8о

равновесия, после то8о а усо меди массой m

= 200 8 при тем-

пературе t

=210°C поместить в алюминиевую чашу алориметра

массой m

= 180 8, содержащую m

= 800 8 воды при температуре

=11°C?

9.5.9. Неоторое оличество вещества массой m

= 220 8 на8ре-

вают до температуры t

= 330 °C и затем помещают в алюминиевую

чашу алориметра массой m

= 90 8, содержащую m

=1508 воды

при температуре t

= 11,5 °C. Конечная температура, измеренная

стелянным термометром массой m

= 17 8, равна t

=33,8°C. Ка-

ова удельная теплоемость это8о вещества? Начальная температу-

ра термометра t

=20°C.

9.5.10. В алюминиевом алориметре массой M = 500 8 нахо-

дится m

= 250 8 воды при температуре t

=19°C. Если в алори-

метр опустить металличесий цилиндр массой m

= 180 8, состоя-

щий из двух частей — алюминиевой и медной, то температура воды

поднимется до θ =27°C. Определите массы алюминия m

и меди m

в цилиндре, если е8о начальная температура t

=127°C.

9.5.11. Образец сплава массой m

= 0,150 8 на8ревают до темпе-

ратуры t

=540°C и быстро помещают в воду массой m

= 400 8 с тем-

пературой t

=10°C, оторая находится в алюминиевой чаше ало-

риметра массой M = 200 8. Конечная температура, установившаяся в

алориметре, t

= 30,5 °C. Найдите удельную теплоемость сплава.

9.5.12. Три химичеси не взаимодействующие жидости мас-

сами m

=1 8, m

= 10 8 и m

= 5 8 налили в алориметр. Началь-

ные температуры жидостей и их удельные теплоемости равны со-

ответственно t

=6°C, t

=–40°C и t

=60°C, c

= 2 Дж/(8 · К),

= 4 Дж/(8 · К) и c

= 2 Дж/(8 · К). Чему равна установившая-

ся температура смеси? Фазовое состояние смеси не изменяется.

9.5.13. В двух одинаовых сосудах находится вода: в одном

массой m

= 0,1 8 при температуре t

=45°C, в дру8ом— m

=0,58 при t

=24°C. В сосуды наливают одинаовое оличество

ртути при одной и той же температуре, после че8о температуры

в сосудах оазываются одинаовыми и равными t =17°C. Найдите

теплоемость сосуда.

 9.5.14. В двух одинаовых сосудах емостью V =1,5л аждый

находится по V

= 1 л воды: в первом — при температуре t

=0°C,

во втором — при температуре t

=100°C. Чтобы выровнять темпе-

185

ратуру воды в сосудах, 8орячую воду доливают доверху в сосуд с хо-

лодной водой, затем воду уже при установившейся температуре пе-

реливают доверху в сосуд с 8орячей водой и т. д. Через сольо пе-

реливаний температуры воды в сосудах будут отличаться не более,

чем на ∆t =1°C? Теплоемости сосудов и остывание воды в процес-

се переливания не учитывать.

9.5.15. В воду массой m = 480 8, имеющую температуру t

=22°C,

бросили усо льда с температурой t

=–8°C. Сольо бросили льда,

если температура смеси установилась равной θ = 12 °C?

9.5.16. Кусо льда массой m

=0,58 с температурой t

=–

10 °C помещен в воду массой m

= 3 8 при температуре t

= 10 °C.

Чему будет равна температура смеси после установления тепло-

во8о равновесия?

9.5.17. В сосуд, содержащий воду массой m

= 0,2 8 при тем-

пературе t

=8°C, опусают лед массой m

= 0,3 8 при температу-

ре t

=–20°C. Каую температуру будет иметь содержимое сосу-

да после установления теплово8о равновесия?

9.5.18. В алориметре находится вода массой m

= 500 8 и лед

массой m

= 54 8 при температуре t

=0°C. В алориметр вводят

водяной пар массой m

= 10 8 при температуре t

=100°C. Найдите

температуру в алориметре после установления теплово8о равно-

весия. Теплоемость алориметра не учитывать.

 9.5.19. В теплоизолированный сосуд, содержащий V

=0,5л

воды при температуре t

=6°C, помещают m

=0,98 льда, имею-

ще8о температуру t

=–25°C. После достижения теплово8о равно-

весия половину воды из это8о сосуда перелили в дру8ой таой же

сосуд, содержащий V

= 2 л воды при температуре t

=18°C, доба-

вив в не8о m

= 0,45 8 льда при температуре = 0 °C. Найдите

температуру θ, оторая установится во втором сосуде. Теплоемос-

ти сосудов не учитывать.

 9.5.20. В теплоизолированном латунном сосуде массой m

= 200 8

находится m

= 1 8 льда при температуре t

=–10°C. В сосуд впус-

ают m

= 200 8 пара при температуре t

= 110 °C. Каая темпера-

тура установится в сосуде? Удельная теплоемость пара в интерва-

ле температур 100 °C – 110 °C равна c

= 1670 Дж/(8 · К).

 9.5.21. В сосуде, из оторо8о быстро выачивают воздух, нахо-

дится m = 20 8 воды при температуре t =0°C. Из-за интенсивно8о

испарения происходит постепенное замораживание воды. Каая

масса воды может быть обращена таим образом в лед?

9.5.22. Вода при соблюдении необходимых условий может

быть переохлаждена до температуры T =263 К. Каая масса льда

образуется, если в таую воду массой M = 1 8 бросить маленьий

усоче льда и вызвать этим замерзание? Удельная теплоемость

переохлажденной воды c =4,18·10

Дж/(8 · К).

t′

186

9.5.23. Лед массой m = 50 8 при температуре 0 °C залючен

в теплонепроницаемую оболочу и подвер8нут давлению p =600атм.

Сольо льда расплавилось, если при повышении давления на

∆p = 138 атм температура плавления льда понижается на ∆T = 1 К?

Считать понижение температуры плавления пропорциональным по-

вышению давления. Удельную теплоту плавления и удельную теп-

лоемость считать таими же, а и при нормальном давлении.

9.6. Тепловое расширение тел

9.6.1. При температуре t

=0°C медная антенна имеет длину

= 80 м. На сольо изменится ее длина при температуре t

=–40°C?

9.6.2. При температуре t

=10°C длина 8азопровода Ставро-

поль—Мосва l = 1300 м. Насольо удлинился бы 8азопровод

при изменении температуры воздуха до t

=40°C, если бы сталь-

ные трубы 8азопровода не были вложены в землю?

9.6.3. Колесо лоомотива имеет диаметр d = 1 м при темпера-

туре t

=0°C. Насольо отличаются расстояния, пройденные по-

ездом за τ = 1 ч зимой и летом при температурах соответственно

=–25°C и t

=+25°C, если в обоих случаях дви8атель делал

n = 480 об/мин?

9.6.4. При температуре t

=5°C длина железной проволои

= 100,29 см, а длина циновой l

= 100,12 см. До аой темпера-

туры надо на8реть проволои, чтобы их длины стали одинаовы?

9.6.5. При из8отовлении неоторо8о прибора оазалось необхо-

димым обеспечить постоянство разности длин железно8о и медно8о

цилиндров при любых изменениях температуры. Каую длину долж-

ны иметь цилиндры при t

=0°C, чтобы разница их длин при всех

температурах была ∆l =10см?

9.6.6. Диаметр латунно8о цилиндра при температуре t

=20°C

должен быть d = 10 см. Допусаемые отлонения от данно8о разме-

ра не должны превышать ∆x = 10 мм. При обработе на тоарном

стане цилиндр на8релся до температуры t

=120°C. Следует ли

учитывать тепловое расширение детали при ее измерении во время

обработи?

9.6.7. Стальной стержень, имеющий площадь поперечно8о се-

чения S =10см

, онцами упирается в две жесто зарепленные

массивные стальные плиты. С аой силой F стержень будет давить

на аждую из плит, если е8о температура повысится на ∆t =15°C?

Модуль Юн8а для стали E =206ГПа.

9.6.8. Однородная прямоу8ольная пластина длиной a и шири-

ной b имеет оэффициент линейно8о расширения α. Найдите изме-

нение площади пластини при повышении температуры на ∆T.

187

9.6.9. Медный шар радиусом r = 5 см на8рели от температу-

ры t

=20°C до t

= 220 °C. Насольо увеличились площадь по-

верхности шара и е8о объем? Коэффициент линейно8о расшире-

ния меди α =1,7·10

–5

–1

9.6.10. Железный цилиндричесий ба, диаметр основания о-

торо8о d = 20 м, а высота h = 8 м, наполнили еросином при темпе-

ратуре t

=15°C. До ао8о уровня можно наливать еросин, чтобы

он не перелился через рай при температуре t

=55°C?

9.6.11. Каой будет разница в объеме спирта и ртути при тем-

пературе t

=0°C, если при температуре t

=25°C они взяты в оди-

наовом объеме V =100см

9.6.12. При температуре t

стержни с температурными оэф-

фициентами линейно8о расширения α

и α

имеют одинаовую

длину, при температуре t

одинаовыми оазываются их объемы.

При аой температуре будут одинаовыми площади поперечно8о

сечения стержней?

9.6.13. Определите плотность цина при температуре t

=150°C,

если е8о плотность при t

=0°C равна ρ

= 7 8/см

9.6.14. Масса уса меди m = 875 8. Определите, при аой тем-

пературе этот усо меди будет иметь объем V = 100 см

. При t

=20°C плотность меди ρ =8,9·10

8/м

9.6.15. Поажите, что изменение плотности ρ вещества при из-

менении температуры на ∆T определяется выражением ∆ρ =–βρ∆T,

8де β — оэффициент объемно8о расширения вещества. Чему равно

относительное изменение плотности свинцово8о шара, температура

оторо8о понизилась от t

=30°C до t

=–30°C?

9.6.16. Кусо стела в воздухе имеет вес P

= 75,352 Н, в воде

при температуре t

=4°C е8о вес P

= 49,261 Н, в воде при темпера-

туре t

=20°Cе8о вес P

= 49,291 Н. Коэффициент объемно8о рас-

ширения стела β =2,5·10

–5

–1

. Определите среднее значение о-

эффициента объемно8о расширения воды в интервале температур

от t

=4°C до t

=20°C.

9.7. Вн'тренняя энер#ия идеально#о #аза

9.7.1. Определите внутреннюю энер8ию 8елия массой m =18

при температуре T = 300 К.

9.7.2. В вертиальном цилиндричесом сосуде площадью попе-

речно8о сечения S =40см

на высоте h = 0,5 м от основания нахо-

дится поршень массой m = 1 8, а под ним — 8аз ар8он. Чему равна

внутренняя энер8ия это8о 8аза?

188

9.7.3. Идеальный одноатомный 8аз изотермичеси сжали из со-

стояния с давлением p

=10

Па и объемом V

= 2 л до объема,

втрое меньше8о первоначально8о. Найдите внутреннюю энер8ию 8аза

в онечном состоянии.

9.7.4. Один моль 8елия на8рели та, что е8о внутренняя энер-

8ия изменилась на ∆U = 600 Дж. Во сольо раз изменилась темпе-

ратура 8елия, если е8о начальная температура T =400К?

9.7.5. Газ, находящийся при температуре t=27°C, на8рет на

∆t =30°. На сольо процентов возросла е8о внутренняя энер8ия?

9.7.6. В зарытом сосуде находится ν = 3 моль 8елия при тем-

пературе t =27°C. На сольо процентов увеличится давление в со-

суде, если внутреннюю энер8ию 8аза увеличить на ∆U =3Дж?

9.7.7. Ар8он в оличестве ν = 5 моль расширяется изобарно та,

что е8о объем увеличивается в n = 5 раз, а внутренняя энер8ия изме-

няется на ∆U = 60 Дж. Определите начальную температуру ар8она.

9.7.8. Идеальный 8аз сжимают поршнем и одновременно на8рева-

ют. Во сольо раз изменится е8о внутренняя энер8ия, если объем 8аза

уменьшить в n = 4 раза, а давление увеличить в k =3раза?

9.7.9. Один моль идеально8о одноатомно8о 8аза при температу-

ре T

= 290 К расширяется изобарно до тех пор, поа е8о объем не

увеличится в n = 2 раза. Затем 8аз на8ревают изохорно та, что е8о

давление увеличивается в k = 3 раза. Найдите изменение внутрен-

ней энер8ии 8аза.

9.7.10. Ар8он в оличестве ν = 1 моль сжимают та, что е8о

объем уменьшается в n = 2 раза. Сжатие происходит по заону

= const. Найдите изменение внутренней энер8ии 8аза. Началь-

ная температура 8аза T

=200К.

9.7.11. Гелий занимает объем V = 2 л при давлении p

= 2 · 10

Па.

Газ расширяется та, что е8о объем увеличивается в n = 2 раза. Рас-

ширение происходит по заону T = αV

, 8де α — положительная по-

стоянная. Найдите изменение внутренней энер8ии 8елия.

 9.7.12. Идеальный одноатомный 8аз в оличестве ν =2моль

расширяется та, что е8о объем увеличивается в n =2раза, при

этом е8о внутренняя энер8ия уменьшается на ∆U = 3,74 Дж. Рас-

ширение происходит по заону p =, 8де α — постоянная. Оп-

ределите начальную температуру 8аза.

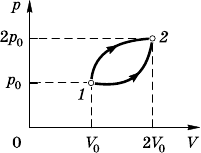
9.7.13. Зависит ли изменение внутрен-

ней энер8ии 8аза от способа е8о перевода из

состояния 1 в состояние 2 (рис. 9.7.1)? Най-

дите изменение внутренней энер8ии при пе-

реходе из состояния 1 в состояние 2, если 8аз

одноатомный; p

=10

Па, V

= 2 л.

9.7.14. Найдите внутреннюю энер8ию

смеси 8азов, состоящей из m

= 20 8 8елия и

= 40 8 ар8она при температуре t = 30 °C.

α V

⁄

Рис. 9.7.1

189

9.7.15. В сосуде находится 8елий массой m

= 10 8 и риптон

массой m

= 84 8. Найдите изменение внутренней энер8ии смеси

при ее на8ревании на ∆T =40К.

9.7.16. Сосуд с ар8оном движется прямолинейно со соростью

v = 50 м/ с. На сольо возрастет температура 8аза, если сосуд оста-

новить? Сосуд теплоизолирован. Теплоемость сосуда не учитывать.

9.7.17. Поршень массой m = 3 8 зарывает с одно8о онца со-

суд объемом V

= 10 л, в отором находится идеальный одноатомный

8аз при температуре T

= 300 К и давлении p

=10

Па (рис. 9.7.2).

Поршню сообщают сорость v = 10 м/с. Найдите температуру 8аза

при е8о масимальном сжатии. Система теплоизолирована. Тепло-

емость поршня и сосуда не учитывать.

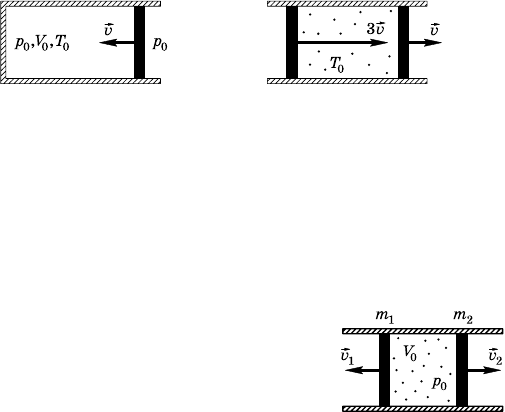
 9.7.18. Зарытый с торцов 8оризонтальный теплоизолирован-

ный цилиндричесий сосуд массой m пере8орожен подвижным

поршнем массой M . m. С обеих сторон от поршня находится по

одному молю идеально8о одноатомно8о 8аза. Коротим ударом сосу-

ду сообщают сорость v, направленную вдоль оси сосуда. Насоль-

о изменится температура ∆T 8аза после затухания олебаний пор-

шня? Трение между поршнем и стенами сосуда, а таже теплоем-

ость поршня не учитывать. Масса 8аза m



n m.

9.7.19. В длинной 8оризонтальной трубе между двумя одинао-

выми поршнями массой m аждый находится один моль одноатом-

но8о 8аза (рис. 9.7.3). При температуре 8аза T

сорости поршней

направлены в одну сторону и равны v и 3v. Каова масимальная

температура 8аза? Труба теплоизолирована, массу 8аза и теплоем-

ость поршней не учитывать.

9.7.20. В длинной пустой 8оризонтальной

теплоизолированной трубе находятся два по-

ршня, массы оторых m

=28 и m

= 1 8.

Между поршнями в объеме V

= 18 л при давле-

нии p

= 10

Па находится одноатомный 8аз

(рис. 9.7.4). Поршни отпусают. Оцените ма-

симальные сорости поршней. Масса 8аза мно-

8о меньше массы поршней.

Рис. 9.7.2 Рис. 9.7.3

Рис. 9.7.4