Туголуков Е.Н. Решение задач теплопроводности методом конечных интегральных преобразований
Подождите немного. Документ загружается.

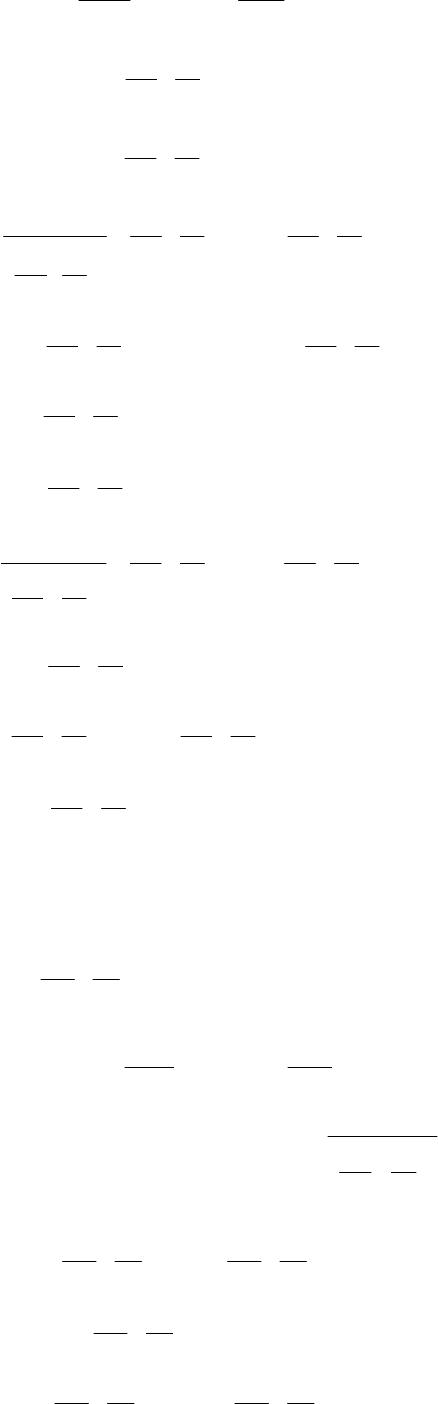
,cos
sin
cos
sin
5,0
cos
sin
cos
sin
5,0
cos5,0
cos5,0
sinsin
,,1
,,11
,,
,,
2
,,1
,,1
1,,
,,
2
,,
,,
,,
1
1
1
ϕ+ϕ+
µ
+
µ
−
−
ϕ+ϕ+
µ
+
µ
µ
+
µ
−
−
ϕ+ϕ+
µ
+
µ
+
+
ϕ+ϕ+
µ
+
µ
µ
+
µ
µ
+
µ
−
−
ϕ−ϕ+
µ
−
µ
−
−
ϕ−ϕ+
µ
−
µ
×
×
µ
−
µ
−
ϕ−ϕ+
µ
−
µ
+
+
ϕ−ϕ+
µ
−
µ
µ
−
µ
µ
−
µ
=
=
ϕ+ϕ+
µ
+
µ
−
−
ϕ−ϕ+
µ
−
µ
=
=
ϕ+
µ
ϕ+
µ
−
−−
−
−
−
∫
∫
∫
−
−
−
nmkbmm
m
n
mb
kb
nmkbmm
m
n
mb
kb
m
m
n
mb
kb
nmkbmm
m
n
mb
kb
nmkbmm
m
n
mb
kb
m
m
n
mb
kb
m
n
mb
kb
nmkbmm
m
n
mb
kb
nmkbmm
m
n
mb
kb
m
m
n
mb
kb
nmkbmm
m
n
mb
kb
nmkbmm
m
n
mb
kb
m
m
n
mb
kb
m
n
bm
bk
R
R
mnmkbmm
m
n
mb
kb
m
R
R
mnmkbmm
m
n
mb
kb
m
R
R
mnm
m
mn
kbm
mb
mkb
m
R
aa
R
aa
R
aa
R
aa
R
aa
R
aa
aa
R
aa
R
aa
R
aa
R
aa
R
aa
R
aa
aa
drr
aa
r
drr
aa
r
dr
a
r
a
r
r
m
m
m
m
m
m
(9.45)
если
,0≠
µ
−
µ
m
n
mb
kb
aa
иначе
()
()
×
µ
+
µ
−ϕ−ϕ−=
=
ϕ+
µ
ϕ+
µ
−
∫
−
2
,,
2
1
2
,,
5,0
cos25,0
sinsin
1
m
n
mb
kb
nmkbmmm
R
R
mnm
m
mn
bkm
mb
mkb
m
aa
RR
dr
a
r
a
r
r
m
m
−
ϕ+ϕ+
µ
+
µ
µ
+
µ
−
−
ϕ+ϕ+
µ
+
µ
+
+
ϕ+ϕ+
µ
+
µ
µ
+
µ
×
−− nmkbmm
m
n
mb
kb
m
m
n
mb
kb
nmkbmm
m
n
mb
kb
nmkbmm
m
n
mb
kb
m
m
n
mb
kb
R
aa
R
aa
R
aa
R
aa
R
aa
,,11
,,
,,
sin
cos
sin

.cos
,,1
ϕ+ϕ+
µ
+
µ
−
− nmkbmm
m
n
mb
kb
R
aa
(9.46)
9.2 Задача теплопроводности для N-слойного сплошного шара
(рис. 9.2)
Рис. 9.2 Сплошной N-слойный шар
(
)
(
) ()
;0,,...,,2,1
,
,
2
,,
1
2
2
2
>τ≤≤=
ρ
+
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
− iii
ii
i
i
ii
i
i
ii
i
ii
RrRNi
c
q
r
rt
r
r
rt
a
rt
(9.47)
(
)
(
)
;0,
iiii
rfrt
=
(9.48)
(
)
;0
,0
1
1
=
∂
τ∂
r
t
(9.49)
(
)
()()
;0,
,
=−τα+
∂
τ∂
λ
cNNNN
N
NN
N
tRt
r
Rt
(9.50)
() ()
(
)
(
)
.1...,,2,1,
,,
;,,
1
1
11
−=
∂
τ∂
λ=
∂
τ∂
λτ=τ
+
+
++
Nj
r
Rt
r
Rt
RtRt
j
jj
j
j
jj
jjjjj
(9.51)
t
cN
α
R
N
r
0
Решение этой задачи получается подстановкой в решения (9.39), (9.40) задачи (9.1) – (9.5) следую-
щих значений чисел, входящих в решение:
.
2
;0;;0
,10
π
=ϕ===
nicNi
BtAR
(9.52)
10 РЕШЕНИЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ ДЛЯ НЕОГРАНИЧЕННОГО БРУСА
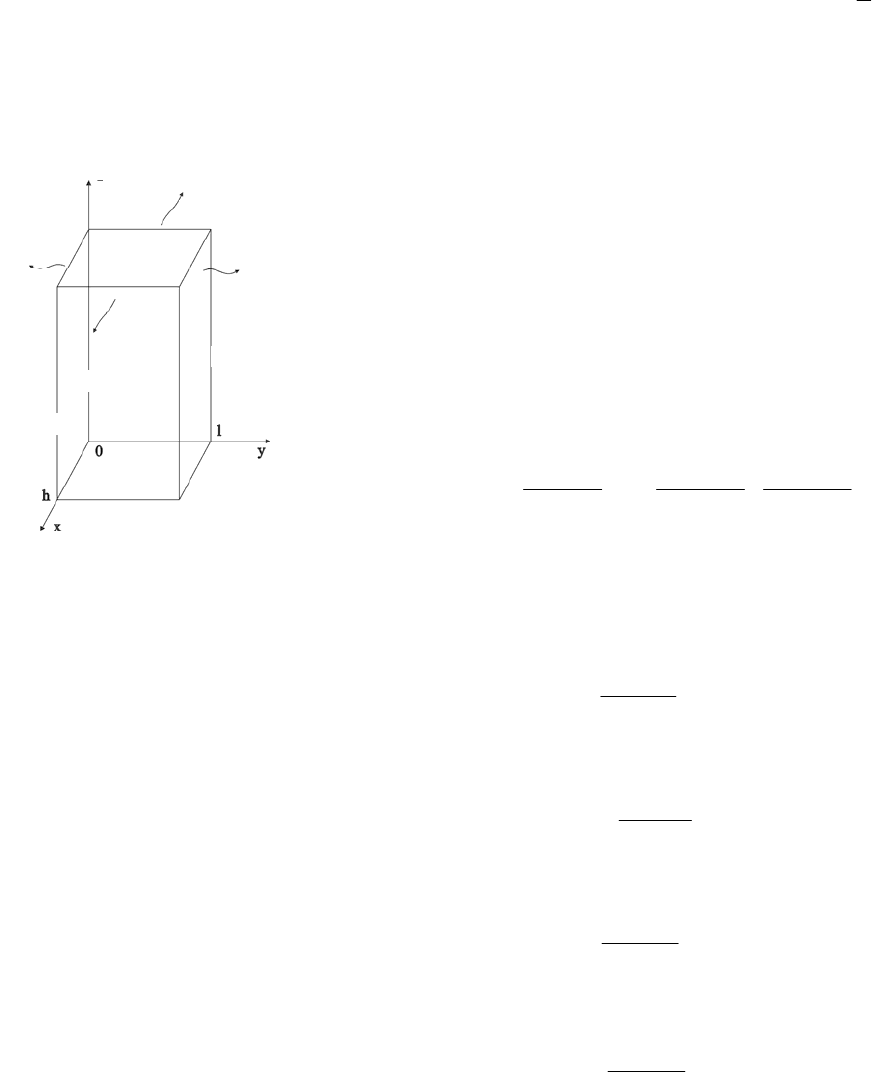
Приводится методика решения нестационарной задачи теплопровод-
ности для неограниченного бруса (рис. 10.1) с произвольным начальным
распределением и неоднородными несимметричными граничными усло-
виями 3-го рода на боковых поверхностях.
Решение может быть использовано для расчета температурных полей
в конструкционных элементах аппаратов с целью нахождения попереч-
ных тепловых потоков в них.
Нестационарное температурное поле в неограниченном брусе пря-
моугольного поперечного сечения описывается следующей системой:
(
)
(
) ()
,
,,,,,,
2
2
2
2
2
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
y
yxt
x
yxt
a
yxt
;0,0,0 >
τ
≤
≤
≤
≤
hylx (10.1)
(
)
(
)
;,0,, yxfyxt
=
(10.2)
(
)
()
()
;0,,0
,,0
11
=−τα−
∂
τ∂
λ
c
tyt
x
yt
(10.3)
(
)
()
()
;0,,
,,
22
=−τα+
∂
τ∂
λ
c
tylt
x
ylt
(10.4)
(
)
()
()
;0,0,
,0,
33
=−τα−
∂
τ∂
λ
c
txt
y
xt
(10.5)
(
)
()
()
.0,,
,,
44
=−τα+
∂
τ∂
λ
c
thxt
y
hxt
(10.6)
Здесь t (x, y, τ) – искомое температурное поле как функция поперечных координат бруса, и времени;
а, λ – соответственно коэффициенты температуропроводности и теплопроводности материала бруса; α
i
,
t
ci
– соответственно коэффициенты теплоотдачи и температуры окружающей среды со стороны боковых
поверхностей бруса.
Решение этой задачи также целесообразно представить в виде суммы
Рис. 10.1 Неограниченный брус
L
y
x
h
0
l
α
4
α
1
α
2
α
3
t
2
t
4
t
1
t
3

(
)
(
)()
,,,,,,
1c
tyxSyxPyxt +
+
τ
=
τ
(10.7)
причем
()
−τ,, yxP решение нестационарной задачи с однородными граничными условиями, а
(
)
−yxS ,
ре-
шение стационарной задачи с неоднородными граничными условиями. Кроме того, для некоторого уп-
рощения выражений решение задачи целесообразно искать относительно температуры окружающей
среды со стороны одной из граней бруса.
(
)
(
)
;0
,,
2
2
2
2
=
∂
∂
+
∂
∂
y
yxS
x
yxS
(10.8)
(
)
()
;0,0
,0
1
=α−
∂
∂
λ yS
x
yS
(10.9)
(
)
()
()
;0,
,
22
=−α+
∂
∂
λ
c
TylS
x
ylS
(10.10)
(
)
()
()
;00,
0,
33
=−α−
∂
∂
λ
c
TxS
y
xS
(10.11)
(
)
()
()
,0,
,
44
=−α+
∂
∂
λ
c
ThxS
y
hxS
(10.12)
где
.
1cicic
ttT −=
(10.13)
Для решения стационарной задачи используем метод конечных интегральных преобразований.
Для исключения координаты x используем интегральное преобразование вида
() ( ) () ()
∫
ρ=
l
dxxWxyxSyU
0
,, (10.14)
причем весовая функция ρ(х) = 1, а ядро интегрального преобразования W(x) является решением вспо-
могательной задачи с однородными граничными условиями:
(
)
()
;0
2
2
2
=µ+ xW
dx
xWd
(10.15)

(
)
()
;00
0
1
=α−λ W
dx
dW
(10.16)
(
)
()
.0
2
=α+λ lW
dx
ldW
(10.17)
Решение ищется с точностью до постоянного множителя в виде:
(
)
(
)
,sin ϕ
+
µ
=
xxW (10.18)
причем числа µ и φ определяются из граничных условий (10.16), (10.17):
;tg
1
α
µλ
=ϕ a
(10.19)
числа µ определяются как последовательные положительные корни уравнения
(
)()
.0cossin
2
=ϕ+µ
µ
λ
+
ϕ
+
µ
α
ll (10.20)
Обратный переход выполняется по стандартной формуле
()
(
)()
,,
1
∑
∞
=
=
n
N
xWyU
yxS
(10.21)
где
=ϕ+µ=ρ=
∫∫
dxxdxxWxN
ll
)(sin)()(
0
2
0
2
()
.)(cos)(sin)(cos)(sin
2
1
ϕ+µϕ+µ−ϕϕ+µ
µ
= lll
(10.22)
Суммирование в (10.21) ведется по значениям µ
n
.
Переходим к изображениям задачи (10.8) – (10.12).
(
)
()
()
∫
=
∂
∂
l
dy
yUd
dxxW
y
yxS
0
2
2
2
2
;
,
(10.23)
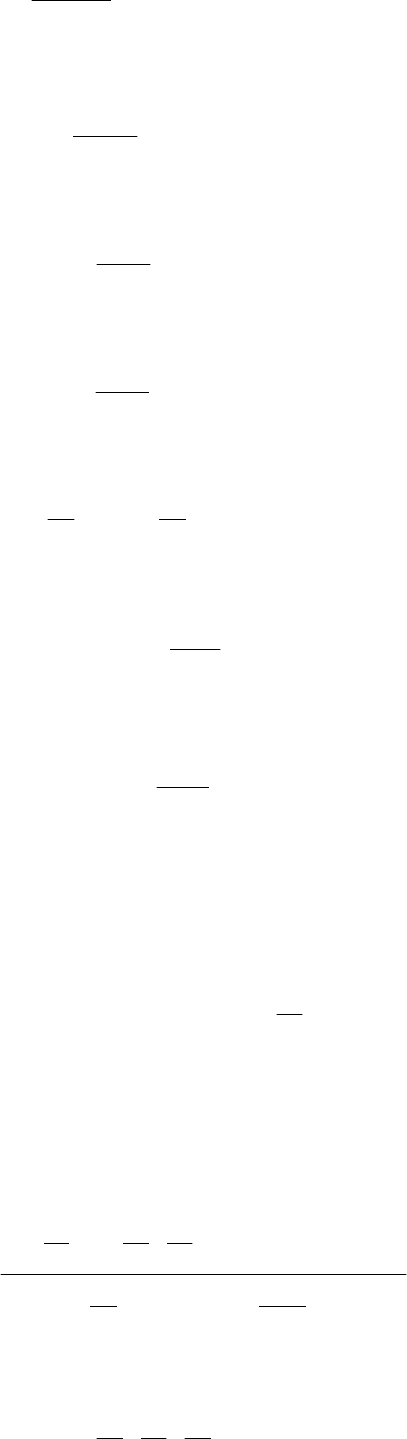
(
)
() ()
∫
+µ−=
∂
∂
l
QyUdxxW
x
yxS
0
2
2
2
,
,
(10.24)
тогда
(
)
()
;0
2
2
2
=+µ− QyU
dy
yUd
(10.25)
(
)
()
;0
0
13
QU
y
U
=α−
∂
∂
λ (10.26)
(
)
()
,
24
QhU
y
hU
=α+
∂
∂
λ
(10.27)
где
() ()
;sin
2
2
2
2
ϕ+µ
λ
α
=
λ
α
= lTlWTQ
cc
(10.28)
() () ( )()
;coscos
33
0
331
ϕ+µ−ϕ
µ
α
−=α−=
∫
l
T
dxxWTQ
c
l
c
(10.29)
() () ( )()
.coscos
44
0
442
ϕ+µ−ϕ
µ
α
=α=
∫
l
T
dxxWTQ
c
l
c
(10.30)
Решением задачи (10.25) – (10.27) является функция
() ( ) ( )
.shch
2
µ
+µ+µ=
Q
yByAyU
(10.31)
А и В определяются из граничных условий (10.26) и (10.27):
() ()()
() ()
;
shch1
chsh
3
22
4
3
4
4
2
3
1
4
2
2
hh
hh
Q
Q
Q
Q
B
µ
α
µλ
−α+µ
α
α
−µλ
µα+µµλ
µ
−
α
−α
µ
−
=
(10.32)
B
Q
Q
A
3
2
3
1
α
λµ
−
µ
−
α
=
. (10.33)

Таким образом, все составляющие решения (10.21) задачи (10.8) – (10.12) полностью определены.
Другая составляющая решения (10.7) задачи (10.1) – (10.6), функция Р (х, у, τ), является решением
нестационарной задачи с однородными граничными условиями:
()
(
)
(
)
,
,,,,,,
2
2
2
2
2
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
y
yxP
x
yxP
a
yxP
;0,0,0 >
τ
≤
≤
≤
≤
hylx (10.34)
(
)
(
)()
;,,0,,
1c
tyxSyxfyxP −−=
(10.35)
(
)
()
;0,,0
,,0
1
=τα−
∂
τ∂
λ yP
x
yP
(10.36)
(
)
()
;0,,
,,
2
=τα+
∂
τ∂
λ ylP
x
ylP
(10.37)
(
)
()
;0,0,
,0,
3
=τα−
∂
τ∂
λ xP
y
xP
(10.38)
(
)
()
.0,,
,,
4
=τα+
∂
τ∂
λ hxP
y
hxP
(10.39)
Решение этой задачи может быть выполнено методом конечных интегральных преобразований по
двум пространственным координатам как одновременно, так и последовательно.
В данном случае последний вариант предпочтительнее, так как для исключения координаты x мо-
жет быть применено преобразование, использованное при решении стационарной задачи (10.8) –
(10.12):
() ( )()()
.,,,
0
∫
ρτ=τ
l
dxxWxyxtyR (10.40)
Обратный переход выполняется по формуле

()
(
)()
,
,
,,
1
∑
∞
=
τ
=τ
n
N
xWyR
yxt
(10.41)
где значение N определяется формулой (10.22).
Функция W(х) является решением задачи (10.15) – (10.17).
Переходим к изображению задачи (10.34) – (10.39):
(
)
(
)
()
;,
,,
2
2
2
2
τµ−
∂
τ∂
=
τ∂
τ∂
yR
y
yR
a
yR
(10.42)
() () ()()
()
()
∫
−−==
l
c
dxxWtyxSyxfyFyR
0
1
;,,0,
(10.43)
(
)
()
;0,0
,0
3
=τα−
∂
τ∂
λ R
y
R
(10.44)
(
)
()
.0,
,
4
=τα+
∂
τ∂
λ hR
y
hR
(10.45)
В свою очередь, задача (10.42) – (10.45) может быть решена с использованием конечного инте-
грального преобразования по координате у:
() ( ) () ( )
∫
ντ=τ
h
dyyZyyRV
0
,, (10.46)
с весовой функцией ν(у) = 1 и формулой обратного перехода

()
(
)()
,,
1
∑
∞
=
τ
=τ
k
M
yZV
yR
(10.47)
где
() ()
.
0
2
∫
ν=
h
dyyZyM
(10.48)
Функция Z(у) является решением вспомогательной задачи
(
)
() ()
;0
22
2
2
=γ+µ− yZyZ
dy
yZd
(10.49)
(
)
()
;00
0
3
=α−λ Z
dy
dZ
(10.50)
(
)
()
.0
4
=α+λ hZ
dy
hdZ
(10.51)
Решение этой задачи с точностью до постоянного множителя имеет вид:
(
)
(
)
,sin φ
+
η
=
yyZ
(10.52)
где числа
222
µ−γ=η и φ определяются из граничных условий (10.50) и (10.51):
,tg
3
α
ηλ
=φ a
(10.53)
а η – последовательные положительные корни уравнения
(
)()
.0sincos
4
=
φ
+
η
α
+
φ
+
η
η
λ
hh
(10.54)
Тогда

() () ( )
∫∫
=φ+η=ν=
hh
dxydyyZyM
0
2
0
2
sin
() () ( ) ( )()
.cossincossin
2
1
φ+ηφ+η−φφ+η
η
= hhh (10.55)
Переходим к изображению задачи (10.42) – (10.45).
(
)
()
,0
22
=τγ+
τ
τ
Va
d
dV
(10.56)
() () () ( ) ( )
()
() () ()
∫∫∫
−−==
hl
c
h
dxdyyZyFxWtyxSyxfdyyZyFV
00
1
0
.,,0
(10.57)
Решение задачи (10.56) – (10.57) имеет вид:
(
)
(
)
(
)
(
)
(
)
(
)
.exp0exp0
22222
τη+µ−=τγ−=τ aVaVV (10.58)
Таким образом, решение задачи (10.1) – (10.6) имеет окончательный вид:
()
(
)
(
) () () ()
.,,
111
1
∑∑∑
∞
=
∞
=
∞
=
τ
++=τ
nmn
c
NM
VyZxW
N
xWyU
tyxt
(10.59)
11 РЕШЕНИЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ
ДЛЯ ПАРАЛЛЕЛЕПИПЕДА
Нестационарное температурное поле параллелепипеда описывается следующей системой:
() ()()()
,
,,,,,,,,,,,,
2
2
2
2
2
2
2
∂
τ∂
+
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
z
zyxt
y
zyxt
x
zyxt
a
zyxt
;0,0,0,0 >
τ
≤
≤
≤
≤
≤
≤
hzsylx (11.1)
