Туголуков Е.Н. Решение задач теплопроводности методом конечных интегральных преобразований
Подождите немного. Документ загружается.


;
0
1
1
1
1
0
1
01
0
1
010
1
1
1
1
,1
µµλ
−
µ
α
µ
α−
µµλ
=
R
a
Y
a
R
a
Y
R
a
JR
a
J
a
D
nnn
nnn
n
(5.74)
;
1
2
0
1
2
0,21
1
0,11
1
0,1
,2
µ
µ
−
µ
+
µ
=
R
a
J
R
a
YDR
a
YDR
a
JC
C
n
n
n
n
n
n
n
n
(5.75)
→
−
µ
µ
−
µ
+
µ
µ
λ
λ
=
1
2
11
2
0
1
1
1,11
1
1,11
2
0
12
21
,2
R
a
YR
a
J
R
a
YDR
a
JCR
a
J
a
a
D
nn
n
n
n
n
n
n
,
1
2
01
2
1
1
1
0,11
1
0,11
2
1
µ
µ
−
µ
+
µ
µ
−
→
R
a
YR
a
J
R
a
YDR
a
JCR
a
J
nn
n
n
n
n
n
(5.76)
−µ
n
n-й положительный корень уравнения
.0
2
2
1
22
2
2
2
02
2
2
1
22
2
2
2
02
=
µ
α
λµ
−
µ
+
µ
α
λµ
−
µ
a
R
Y
aa
R
YD
a
R
J
aa
R
JC
(5.77)
Применяя преобразование (5.65) к задаче (5.60) – (5.64), переходим к изображениям:
(
)
()
;0,
,
2
=τµµ+
τ
τµ
nn
n
U
d
Ud
(5.78)
() () ()()()
∑
∫
=
−
µ−
λ
=µ
2
1
1
.,0,
m
R
R
mnmmmmmmm
m
m
n
m
m
drrWrSrfr
a
U (5.79)
Решением задачи (5.78) – (5.79) является функция
(
)
(
)
(
)
.exp0,,
2
τµ−µ=τµ
nnn
UU (5.80)
Таким образом, решение исходной задачи (5.45) – (5.49) имеет вид:
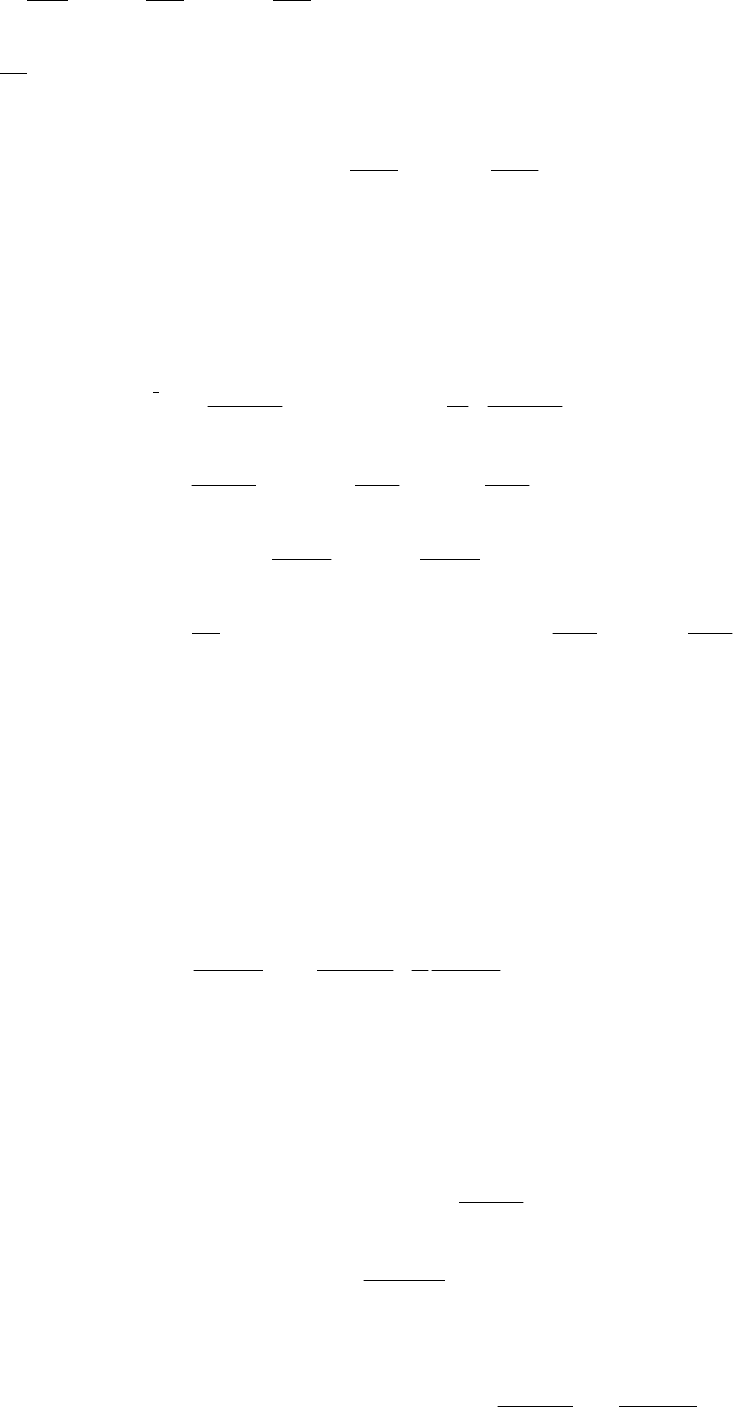
() ()
()
() ()()
∑
∫
∑
=
∞
=
−
×−−
λ
τµ−×
×
µ
+
µ
++=τ
2
1
2
2
0,0,
1
,
1
lnexp
1
ln,
m
R
R
mmmmmm
m
m
n
i
in
ni
i
in
ni
n
nm
iiiii
m
m
rBArfr
a
a
r
YD
a
r
JС
Z
rBArt
.
0,0, m
m
mn
ni
m
mn
ni
dr
a
r
YD
a
r
JС
µ
+
µ
×
(5.81)
Средняя температура по слоям равна
() () ()
()
()
()
() ()()
.ln
exp
lnln
2
,
2
2
1
0,0,
2
2
1
1,
1
1,
1
1,1,
1
,
1
2
1
2
2
1
22
1
2
1
1
∑
∫
∑
∫
=
−−
−
∞
=
−−
−−
−
−
µ
+
µ
−−
λ
×
×τµ−
µ
+
µ
−
−
µ
+
µ
µ
+
+−
−
+−=τ
−
=τ
m
R
R
m
m
mn
ni
m
mn
nimmmmmm
m
m
n
i
in
ni
i
in
ni
i
i
in
ni
i
in
nii
n
nmn
i
iiii
ii
ii
iiii
R
R
i
ii
i
m
m
i
i
dr
a
r
YD
a
r
JСrBArfr
a
a
R
YD
a
R
JСR
a
R
YD
a
R
JСR
Z
a
RRRR
RR
BB
Adrrtr
RR
t
(5.82)
5.4 Задача теплопроводности для сплошного 2-слойного цилиндра
(
)
(
)
(
)
;0,,2,1,
,
1
,,
1
2
2
2
>τ≤≤=
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
− iii
i
ii
i
i
ii
i
ii
RrRi
r
rt
r
r
rt
a
rt
(5.83)
(
)
(
)
;0,
iiii
rfrt
=
(5.84)
(
)
;0
,0
1
1
=
∂
τ∂
r
t
(5.85)
(
)
()()
;0,
,
2222
2
22
2
=−τα+
∂
τ
∂
λ
c
tRt
r
Rt
(5.86)
()()
(
) ()
.
,,
;,,
2
12
2
1
11
11211
r
Rt
r
Rt
RtRt
∂
τ∂
λ=
∂
τ
∂
λτ=τ
(5.87)
Решение этой задачи получается подстановкой в решения (5.81), (5.82) задачи (5.45) – (5.49) сле-
дующих значений чисел, входящих в решение:
,0;1;0;;0
,1,120
==
=
=
=
nnici
DCBtAR (5.88)
а также исключением членов, содержащих
()
.,,ln
1
0
1
1
0
00
µ
µ
a
R
Y
a
R
YR
nn
6 РЕШЕНИЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ ДЛЯ КОНЕЧНОГО ЦИЛИНДРА
Решение задачи нестационарной теплопроводности для
сплошного ограниченного цилиндра (рис. 6.1) с произвольным начальным
распределением и неоднородными несимметричными граничными ус-
ловиями 3-го рода на торцовых и боковой поверхностях представлено
ниже.
Решение задачи может быть использовано для расчета
нестационарных температурных полей и тепловых потоков в изделиях
цилиндрической формы в условиях, когда необходим учет теплообмена на
торцах, элементах аппаратов, конструкций и сооружений, имеющих
форму конечного цилиндра, а также для определения условий протекания
теплообменных процессов в перечисленных выше случаях по
измеренным температурным полям.
За точку отсчета удобнее принять температуру среды со стороны боковой поверхности цилиндра, что
дает возможность использовать однородные граничные условия на этой поверхности. При этом задача
имеет вид:
() ()
(
)
(
)
;0;0;
,,1,,,,,,
2
2
2
2
Rrlx
r
rxt
r
r
rxt
x
rxt
a
rxt
<<<<
∂
τ∂
+
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
(6.1)
(
)
(
)
;,,,
2c
trxfrxt −
=
τ
(6.2)
(
)
;0
,0,
=
∂
τ∂
r
xt
(6.3)
(
)
()()
;0,,0
,,0
211
=+−τα−
∂
τ∂
λ
cc
ttrt
x
rt
(6.4)
(
)
()()
;0,,
,,
233
=+−τα+
∂
τ∂
λ
cc
ttrlt
x
rlt
(6.5)
α
t
R
r
α
0
t
α
t
x
l

(
)
()
.0,,
,,
2
=τα+
∂
τ∂
λ Rxt
r
Rxt
(6.6)
Проведем интегральное преобразование одновременно по координатам x и r. Для нахождения ядра
интегрального преобразования Р (x, r) необходимо решить вспомогательную задачу с однородными
граничными условиями:
(
)
(
) ()
()
;,
,1,,
2
2
2
2
2
rxP
r
rxP
r
r
rxP
x
rxP
µ−=
∂
∂
+
∂
∂
+
∂
∂
(6.7)
(
)
;0
0,
=
∂
∂
r
xP
(6.8)
(
)
()
;0,0
,0
1
=α−
∂
∂
λ rP
x
rP
(6.9)
(
)
()
;0,
,
3
=α+
∂
∂
λ rlP
x
rlP
(6.10)
(
)
()
.0,
,
2
=α+
∂
∂
λ RxP
r
RxP
(6.11)
Эта задача может быть решена любым аналитическим методом, в том числе и интегральными пре-
образованиями по одной из оставшихся координат. При этом ищется частное решение с точностью до
постоянного множителя.
Для решения задачи (6.7) – (6.11) по тем же правилам составляем еще одну задачу:
(
)
()
;
2
2
xK
xd
xKd
ν−=
(6.12)
(
)
()
;00
0
1
=α−λ K
xd
dK
(6.13)
(
)
()
.0
3
=α+λ lK
xd
lKd
(6.14)
Задача (6.12) – (6.14) имеет решение с точностью до постоянного множителя:
(
)
(
)
,sin ϕ
+
ν
=
xxK
(6.15)
где

,arctg
1
α
νλ
=ϕ
(6.16)
а −ν
n
n-й положительный корень уравнения
()
.tg
3
α
νλ
−=ϕ+νl
(6.17)
Изображение задачи (6.7) – (6.11) находим по формуле:
() ( ) ()
.,
0
∫
=
l
dxxKrxPrU
(6.18)
При этом в изображениях имеем:
(
)
(
)
()
;
1
2
2
2
rU
rd
rUd
r
dr
rUd
γ−=+
(6.19)
(
)
;0
0
=
∂
∂
r
U
(6.20)
(
)
()
,0
2
=α+λ RU
rd
RUd
(6.21)
где .
222
ν−µ=γ (6.22)
Здесь
() ( )
,
0
rJrU
γ
= (6.23)
причем γ – положительный корень уравнения
() ()
;0
01
2
=γ−γ
α
γλ
RJRJ
(6.24)
() ()
−rJrJ
01
, Бесселевы функции.
Теперь может быть записано общее решение задачи (6.7) – (6.11):

() ()()
,sin
1
,
1
0
1
∑∑
∞
=
∞
=
γϕ+ν=
n
mnn
m
xn
rJx
N
rxP
(6.25)
где
−
nx
N
постоянные коэффициенты.
Для решения задачи (6.1) – (6.6) необходимо частное решение с точностью до постоянного множи-
теля, т.е.
(
)
(
)()
.sin,
0
rJxrxP
γ
ϕ
+
ν
=
(6.26)
Переходим к изображениям задачи (6.1) – (6.6) по формуле:
() ( ) ( )
∫∫
τ=τ
lR
dxdrrxrPrxtT
00
,,,, (6.27)
где r – весовая функция.
В результате в изображениях получаем задачу:
(
)
()
(
)
;
2
STa
d
Td
+τµ−=
τ
τ
(6.28)
(
)
.0 FT
=
(6.29)
Решение этой задачи в изображениях:
()
()
.exp
2
22
τµ−
µ
−+
µ
=τ a
S
F
S
T
(6.30)
Здесь
;
222
ν−µ=γ
(6.31)
F – изображение начального условия:

()()()()
∫∫
γϕ+ν−=
lR
c
dxrdrrJxtrxfF
00
02
;sin,
(6.32)
S учитывает неоднородность граничных условий по линейной координате:
() ()()()()
.sinsin
21
1
23
3
1
ϕ−
λ
α
+ϕ+ν−
λ
α
γ
γ
=
cccc
ttlttRJ
R
S
(6.33)
Обратный переход выполняется по формуле:
() () ( )
∑∑
∞
=
∞
=
τ=τ
11
.,
1
,,
nm
mn
mn
rxPT
N
rxt (6.34)
() ()()
()
×γ+γ==
∫∫
lR
mmmnmn
rJRJ
R
rxrPN
00
2
0
2
1
2
2
4
,
() () ( ) ( )()
.cossincossin
1
ϕ+νϕ+ν−ϕϕ
ν
+×
nnnnnn
n
xxl (6.35)
Таким образом, окончательное решение задачи (6.1) – (6.6) имеет вид:
()
()
×
τµ−
µ
−+
µ
+=τ
∑∑
∞
=
∞
=
11
2
2
exp
1
,,
nm
mn
mnmnmn
c
a
S
F
S
N
trxt
(
)
(
)
;sin
0
rJx
mnn
γ
ϕ
+
ν
×
(6.36)
()
()
×
τµ−
µ
−+
µ
+=τ
∑∑
∞
=
∞
=
11
2
2
exp
1
nm
mn
mnmnmn
c
a
S
F
S
N
tt
() ( )()()
.coscos
2
1
RJl
lr
mnnn
mn
γϕ+ν−ϕ
γν
×
(6.37)
Все величины, входящие в (6.36) и (6.37), определены уравнениями:

).24.4();16.4();17.4(
);32.4();31.4();33.4();35.4(
→γ→ϕ→ν
→→µ→→
mnn
mnmn
FSN
Здесь
mn
µ
имеет размерность [1/м], что определяется видом (6.25) и характерно для выбранного ме-
тода решения задачи (6.1) – (6.6).
Интеграл в (6.31) берется аналитически, если в качестве f (x, r) использовать (6.36) при τ = τ
k
для кон-
ца предыдущего периода (интервала по τ).
Если начальное распределение температуры является решением задачи теплопроводности для пре-
дыдущего временного интервала:
(
)
(
)
pp
rxtrxf
τ
=
,,, (6.38)
(индекс р указывает на принадлежность предыдущему интервалу), тогда параметр
() ( ) ( )
∫∫
τ=τ
lR
dxrdrxrPrxtT
00
,,,,
(6.39)
входящий в решение, может быть выражен алгебраически, так как интегралы берутся аналитически
(стандартными преобразованиями сводятся к табличным):
()
()
×
τµ−
µ
−+
µ
+=τ
∑∑
∞
=
∞
=
11
2
2
exp
1
,,
nm
mn
mnmnmn
c
a
S
F
S
N
trxt
(
)
(
)
;sin
0
rJx
mnn
γ
ϕ
+
ν
×
(6.40)
где
()() ()()()
RJRJRJRJ
R
S
mmpmmmpmp
mmp
c
γγγ−γγγ
γ−γ
=
1001
22
(6.41)
при условии
;
mmp
γ≠γ

()()
(
)
,
2
2
1
2
0
RJRJ
R
S
mmc
γ−γ= (6.42)
если
;
mmp
γ≠γ
()
()()()()
−ϕ−ϕ−ϕ−ϕ+ν−ν
ν−ν
=
nnpnnpnnp
nnp
l
lS sinsin
2
1
()
()()()()
,sinsin
2
1
nnpnnpnnp
nnp
l ϕ+ϕ−ϕ+ϕ+ν+−ν
ν+ν
−
(6.43)
если
nnp
ν≠ν , и
() () ( ) ( )()
,cossincossin
1
2
1
ϕ+νϕ+ν−ϕϕ
ν
+=
nnnnnn
n
l
lllS
(6.44)
если
nnp
ν≠ν
.
В случае, когда
()
,tsnoc,
0
== trxf что характерно для начала процесса, выражения соответственно
упрощаются. Для параметра F получаем выражение
() ( )()()
.coscos
1
00
RJ
R
ltF
m
m
nnn
n
γ
γ
ϕ+ν−ϕ
ν
=
(6.45)
7 РЕШЕНИЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ ДЛЯ ПОЛОГО
ОГРАНИЧЕННОГО ЦИЛИНДРА С ФУНКЦИОНАЛЬНО
МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРОЙ ОКРУЖАЮЩЕЙ СРЕДЫ
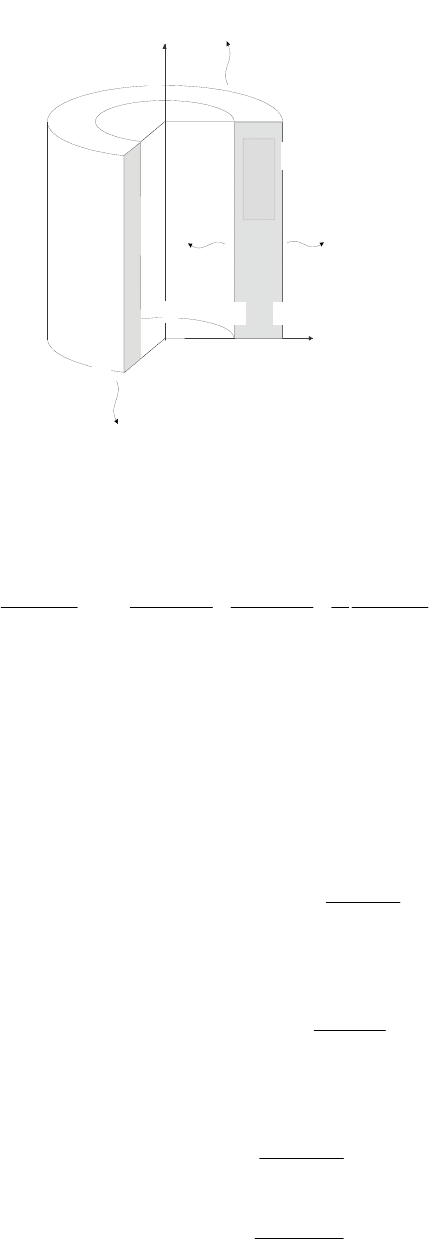
СО СТОРОНЫ БОКОВЫХ ПОВЕРХНОСТЕЙ
Рассмотрим другой пример решения задачи теплопроводности,
используемой при моделировании температурных полей
элементарных областей производственного оборудования
химической промышленности.
Цилиндрические стенки аппаратов, охваченные рубашкой, а
также трубки кожухотрубчатых теплообменников омываются теп-
лоносителем, температура которого меняется во времени и по
длине зоны теплообмена.
Температурное поле такой стенки моделируется решением задачи
теплопроводности для полого ограниченного цилиндра с
функционально меняющейся температурой окружающей среды со
стороны боковых поверхностей (рис. 7.1).
В приводимой постановке задача записана относительно
температуры окружающей среды с торцовых поверхностей.
() () () ()
,
,,1,,,,,,
2
2
2
2
2
∂
τ∂
+
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
r
rxt
r
r
rxt
x
rxt
a
rxt
;0,,0
10
>τ≤≤≤≤ RrRlx
(7.1)
(
)
(
)
;,0,,
0c
trxfrxt −
=
(7.2)
(
)
()
;0,,0
,,0
1
=τα−
∂
τ∂
λ rt
x
rt
(7.3)
(
)
()
;0,,
,,
2
=τα+
∂
τ∂
λ rlt
x
rlt
(7.4)
(
)
()()()
;0,,,
,,
000
0
=+τ−τα−
∂
τ∂
λ
cv
txtRxt
r
Rxt
(7.5)
(
)
()()()
.0,,,
,,
01
1
=+τ−τα+
∂
τ∂
λ
ccc
txtRxt
r
Rxt
(7.6)
Для торцевых поверхностей могут быть выбраны иные граничные условия с соответствующей по-
становкой задачи.
0
rR
0
R
1
x
λ
c
ρ
t(x,τ
)
c
α
c
..
.
.
l
t
c0
t
c0
α
0
α
1
α
2
t(x,τ)
v
Рис. 7.1. Полый ограниченный
0
l
x
r
R
1
R
0
α
1
α
0
α
c
α
2
t
c
0
t
c
0
t
(
x
t
(
x
λ
c
ρ
