Туголуков Е.Н. Решение задач теплопроводности методом конечных интегральных преобразований
Подождите немного. Документ загружается.

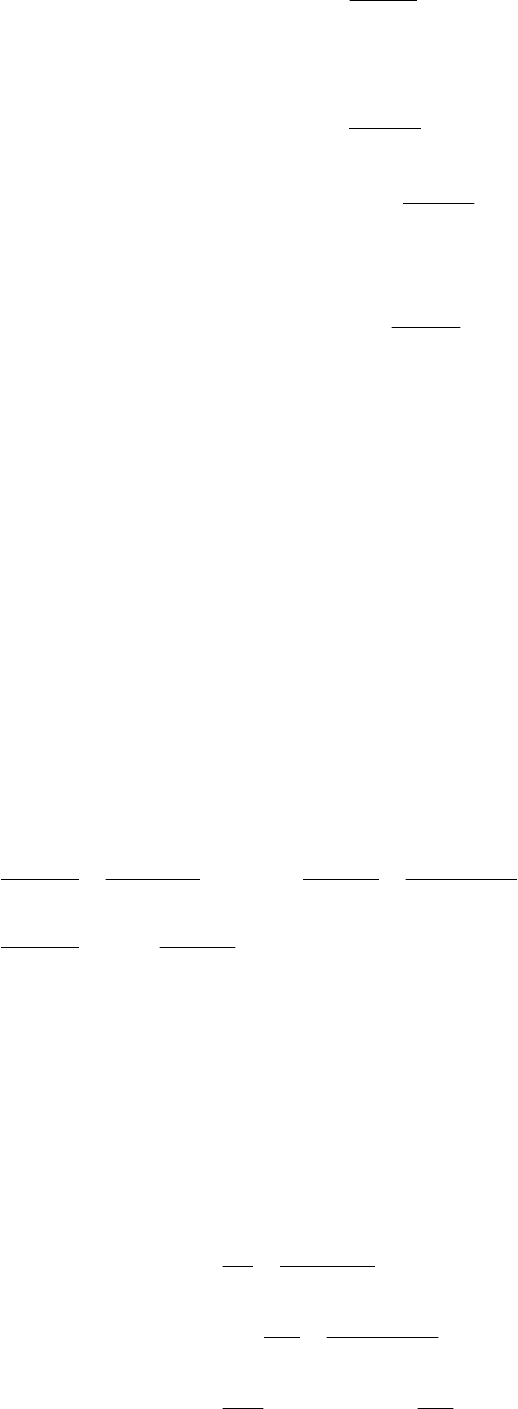
(
)
()()
;0,
,
424
2
2
=−α+
∂
∂
λ
c
trht
y
rht
(8.39)
(
)
()()
;0,
,
222
2
2
=−α+
∂
∂
λ
c
tRyt
r
Ryt
(8.40)
(
)
;0
0,
2
=
∂
∂
r
yt
(8.41)
(
)
()
.
,0
2
2
rm
y
rt
−=
∂
∂
λ
(8.42)
Решение этой задачи может быть записано формально путем соответствующей замены величин,
входящих в решение задачи (8.11) – (8.15):
.,,,
,,,,
,,,,,
1111
1134
12341212
nnnnnnnn
nnnnnncc
cc
ZZDDCCSS
KKMMtt
ttxy
→→→→
→→µ→γ→
→α→αα→αλ→λ→
(8.43)
Теперь числа М
1
и М могут быть найдены из условия равенства температур (8.9) и неразрывности
тепловых потоков (8.10) на поверхности контакта тел:
() ()
() ()
γ
−=
µ
+
+
−
γ
=
+
+
−
µ
∑∑
∑∑
∞
=
∞
=
∞
=
∞
=
.
;
1
1
1
0
1
0
1
1
111
1
1
0
1
0
n
n
n
n
n
n
n
n
n
nnn
n
n
n
n
n
nnn
n
n
n
M
Z
rJ
M
Z
rJ
K
D
CMS
Z
rJ
K
D
CMS
Z
rJ
(8.44)
Будем последовательно умножать левые и правые части равенства на
()
k
rrJ µ
0
и интегрировать в
пределах от 0 до R. В результате получаем систему уравнений:
()
()()
() ()()
γµ=µ
γµ
+
+
−=
=µ
+
+
−
∫
∑
∫
∫
∑
∫
∞
=
∞
=
.
1
,
1
1
0
0
0
1
1
0
2
0
0
0
01
1
111
1
1
0
2
drrJrrJ
Z
drrrJ
Z
M
drrJrrJK
D
CMS
Z
drrrJK
D
CMS
Z
nk
R
n
n
R
k
k
k
nk
R
n
n
nnn
n
n
R
kok
k
kkk
k
(8.45)

Здесь использовано свойство ортогональности Бесселевых функций:
()()
∫
=µµ
R
kn
drrJrrJ
0
00
,0
если
kn ≠
. (8.46)
Если в расчетах используются N членов ряда, система (8.45) представляет собой систему линейных
уравнений, из которой определяются числа
,
1k
M
;
k
M
.1 Nk
≤
≤
Вводя соответствующие обозначения, получим систему (8.45) в виде:
=−
≤≤=−
∑
∑
=
=
,0
;1,
1
1
11
N
n
nnkk
k
N
n
nnnkkk
MHM
NkLMGHMG
(8.47)
где
;;
1
1
1
k
k
k
k
k
k
D
C
G
D
C
G ==
(8.48)
(
)
(
)()()
;
22
1001
kn
knkknn
n
nk
RJRJRJRJ
Z
R
H
γ−µ
γµγ−γµµ
=
(8.49)
.
1
1
1
1
−++−=
∑
=
k
k
k
N
n
nkk
k
k
k
K
D
S
HK
D
S
L
(8.50)
Подставляя из второго уравнения системы (8.47) М
k
в первое, получаем систему N линейных урав-
нений относительно неизвестных М
1n
:
()
;1,
11
1
NkLMGGH
knnk
N
n
nk
≤≤−=+
∑
=
(8.51)
затем определяются числа М
k
:
.1,
1
NkMHM
n
N
n
nkk
≤≤=
∑
=
(8.52)

9 РЕШЕНИЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ ДЛЯ N-СЛОЙНОГО ПОЛОГО И
СПЛОШНОГО ШАРА С РАСПРЕДЕЛЕННЫМ
ИСТОЧНИКОМ ТЕПЛА
Приводится методика решения нестационарной задачи теплопроводности для N-слойных полого и
сплошного шара (рис. 9.1.) с произвольным начальным распределением, граничными условиями 4-го
рода на поверхностях контакта слоев и неоднородными несимметричными граничными условиями 3-го
рода на внешних границах.
Решение задачи может быть использовано для расчета нестационарных температурных полей и те-
пловых потоков в многослойных сферических изделиях, сферических элементах аппаратов, конструк-
ций и сооружений, в сферических образцах, у которых теплофизические параметры функционально за-
висят от температуры, а также для определения условий протекания теплообменных процессов в
перечисленных выше случаях по измеренным температурным полям.
9.1 Задача теплопроводности для N-слойного полого шара
(
)
(
) ()
;0,,...,,2,1
,
,
2
,,
1
2
2
2
>τ≤≤=
ρ
+
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
− iii
ii
i
i
ii
i
i
ii
i
ii
RrRNi
c
q
r
rt
r
r
rt
a
rt
(9.1)
(
)
(
)
;0,
iiii
rfrt
=
(9.2)
(
)
()()
;0,
,
1011
1
01
1
=−τα−
∂
τ∂
λ
c
tRt
r
Rt
(9.3)
(
)
()()
;0,
,
=−τα+
∂
τ∂
λ
cNNNN
N
NN
N
tRt
r
Rt
(9.4)
() ()
(
)
(
)
,
,,
;,,
1
1
11
+
+
++
∂
τ
∂
λ=
∂
τ
∂
λτ=τ
j
jj
j
j
jj
jjjjj
r
Rt
r
Rt
RtRt
.1...,,2,1
−
=
Nj
(9.5)

Рис. 9.1 N-слойный полый шар
Решение задачи (9.1) – (9.5) с неоднородными граничными условиями также целесообразно пред-
ставить, как сумму стационарной и нестационарной составляющих:
(
)
(
)
(
)
,...,,2,1,,, NirPrSrt
iiiiii
=
τ
+
=
τ
(9.6)
где
()
−
ii
rS решение стационарной задачи с неоднородными граничными условиями
(
)
(
)
;,...,,2,1,0
2
1
2
2
iii
i
ii
i
i
ii
RrRNi
dr
rdS
r
dr
rSd
≤≤==+
−
(9.7)
(
)
()()
;0
1011
1
01
1
=−α−λ
c
tRS
dr
RdS
(9.8)
(
)
()()
;0=−α+λ
cNNNN
N
NN
N
tRS
dr
RdS
(9.9)
() ()
(
)
(
)
,;
1
1
11
+
+
++
λ=λ=
j
jj
j
j
jj
jjjjj
dr
RdS
dr
RdS
RSRS
.1...,,2,1
−
=
Nj (9.10)
Решение стационарной задачи (9.7) – (9.10) имеет вид:
()
,
i
i
iii
r
B
ArS +=
(9.11)
где
;
111111
1
1
1
1
1010
11
1
1
∑
−
=
+
λ
−
λ
λ
+
α
+
λ
λ
−
α
−
λ
λ
−
=
N
k
kkkNNNN
ccN
RRRRR
tt
B
(9.12)
t
cN
α
R
N
r
R
0

;1
01
1
0
1
11
+
α
λ
−=
RR
B
tA
c
(9.13)
;1,...,2,1,
1
1
1
1
−=
λ
λ
=
+
+
NjBB
j
j
(9.14)
;1
1
1
λ
λ
−+=
+
+
j
j
j
j
jj
R
B
AA
(9.15)
()
−τ,
ii
rP решение нестационарной задачи с однородными граничными условиями:
(
)
(
) ()
;0,,...,,2,1
,
,
2
,,
1
2
2
2
>τ≤≤=
ρ
+
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
− iii
ii
i
i
ii
i
i
ii
i
ii
RrRNi
c
q
r
rP
r
r
rP
a
rP
(9.16)
(
)
(
)()
;0,
iiiiii
rSrfrP
−
=
(9.17)
(
)
()
;0,
,
011
1
01
1
=τα−
∂
τ∂
λ RP
r
RP
(9.18)
(
)
()
;0,
,
=τα+
∂
τ∂
λ
NNN
N
NN
N
RP
r
RP
(9.19)
() ()
(
)
(
)
,
,,
;,,
1
1
11
+
+
++
∂
τ
∂
λ=
∂
τ
∂
λτ=τ
j
jj
j
j
jj
jjjjj
r
RP
r
RP
RPRP
.1...,,2,1
−
=
Nj (9.20)
Решение задачи (4.16) – (4.20) получено методом конечных интегральных преобразований. Для ис-
ключения координаты r, вдоль которой свойства тела изменяются ступенчато, используется формула
перехода к изображениям:
() () ( ) ( )
∑
∫
=
−
µτρ
λ
=τµ
N
m
R
R
mmmmmm
m
m
m
m
drrWrPr
a
U
1
2
1
,,,, (9.21)

где
()
−=ρ
2
mm
rr весовая функция, являющаяся решением уравнения
(
)
(
)
.0
2
=
ρ
−
ρ
r
r
dr
rd
(9.22)
Обратный переход осуществляется по формуле:
()
(
)( )
,
,,
,
1
∑
∞
=
µτµ
=τ
n
n
nmmn
mm
Z
rWU
rP
(9.23)
где
()
,,
1
22
1
2
∫
∑
−
µ
λ
=
=
m
m
R
R
mnmmm
N
m
m
m
n
drrWr
a
Z (9.24)
а ядро интегрального преобразования
(
)
µ
,
mm
rW является решением вспомогательной задачи (здесь µ –
параметр):
(
)
(
)
()
;,...,,2,1
,0,
,2,
1
2
2
2
2
mmm
mm
mm
mm
m
m
mm
RrRNm
rW
adr
rdW
r
dr
rWd
≤≤=
=µ
µ
+
µ
+
µ
−
(9.25)
(
)
()
;0,
,
011
1
01
1
=µα−
µ
λ RW
dr
RdW
(9.26)
(
)
()
;0,
,
=µα+
µ
λ
NNN
N
NN
N
RW
dr
RdW
(9.27)
() ()
(
)
(
)
,
,,
;,,
1
1
11
+
+
++
µ
λ=
µ
λµ=µ
j
jj
j
j
jj
jjjjj
dr
RdW
dr
RdW
RWRW
.1...,,2,1
−
= Nj (9.28)
Подставляя решение задачи (9.25)
()
ϕ+
µ
=µ
nm
m
mn
m
nm
nmm
a
r
r
С
rW
,
,
sin, (9.29)
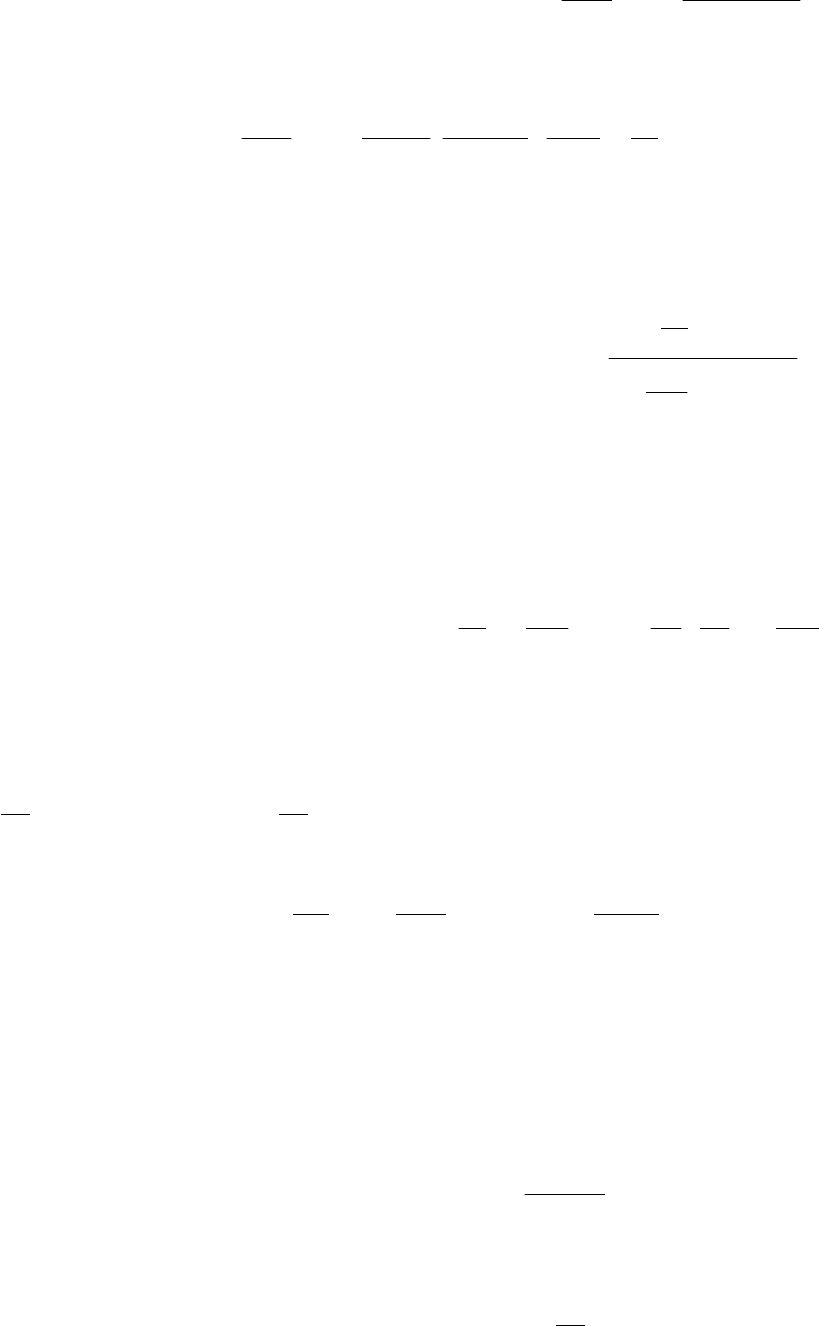
в граничные условия (9.26) – (9.28), находим числа
nnmnm
C µϕ ,,
,,
, причем
n
C
,1
принимаются равными 1:
()
;arctg
1011
01
1
0
,1
λ+α
µλ
+
µ
−=ϕ
Ra
R
a
R
nn
n
(9.30)
,tgarctg
,
1
1
1
1
,1
ϕ+
µλµ
+
λ−λ
µλ
+
µ
−=ϕ
+
+
+
+
+
nmm
m
n
m
mn
m
mm
nm
m
m
mn
nm
R
aaR
a
a
R
;1...,,2,1
−
=
Nm
(9.31)
;
sin
sin
,1
1
,
,,1
ϕ+
µ
ϕ+
µ
=
+
+
+
nmm
m
n
nmm
m
n
nmnm
R
a
R
a
CC
(9.32)
−µ
n
n-й положительный корень уравнения
.0sin
1
cos =
ϕ+
µ
−
λ
α
+
ϕ+
µµ
N
N
N
NN
N
N
N
N
N
a
R
Ra
R
a
(9.33)
Тогда
()
×
λ
=µ
λ
=
∑
∫
∑
==
−
2
,
1
2
22
1
2
5,0,
1
nm
N
m
m
m
R
R
mnmmm
N
m
m
m
n
C
a
dxrWr
a
Z
m
m
.2sin2sin
2
,
1
,1
ϕ+
µ
−
ϕ+
µ
µ
−−×
−
−
nm
m
mn
nm
m
mn
n
m
mm
a
R
a
Ra
RR
(9.34)
Применяя преобразование (9.19) к задаче (9.14) – (9.18), переходим к изображениям:
(
)
()
;,
,
2
nnn
n
QU
d
dU
=τµµ+
τ
τµ
(9.35)
() () ()()()
∑
∫
=
−
µ−
λ
=µ
N
m
R
R
mnmmmmmmm
m
m
n
m
m
drrWrSrfr
a
U
1
2
2
1
,,0, (9.36)
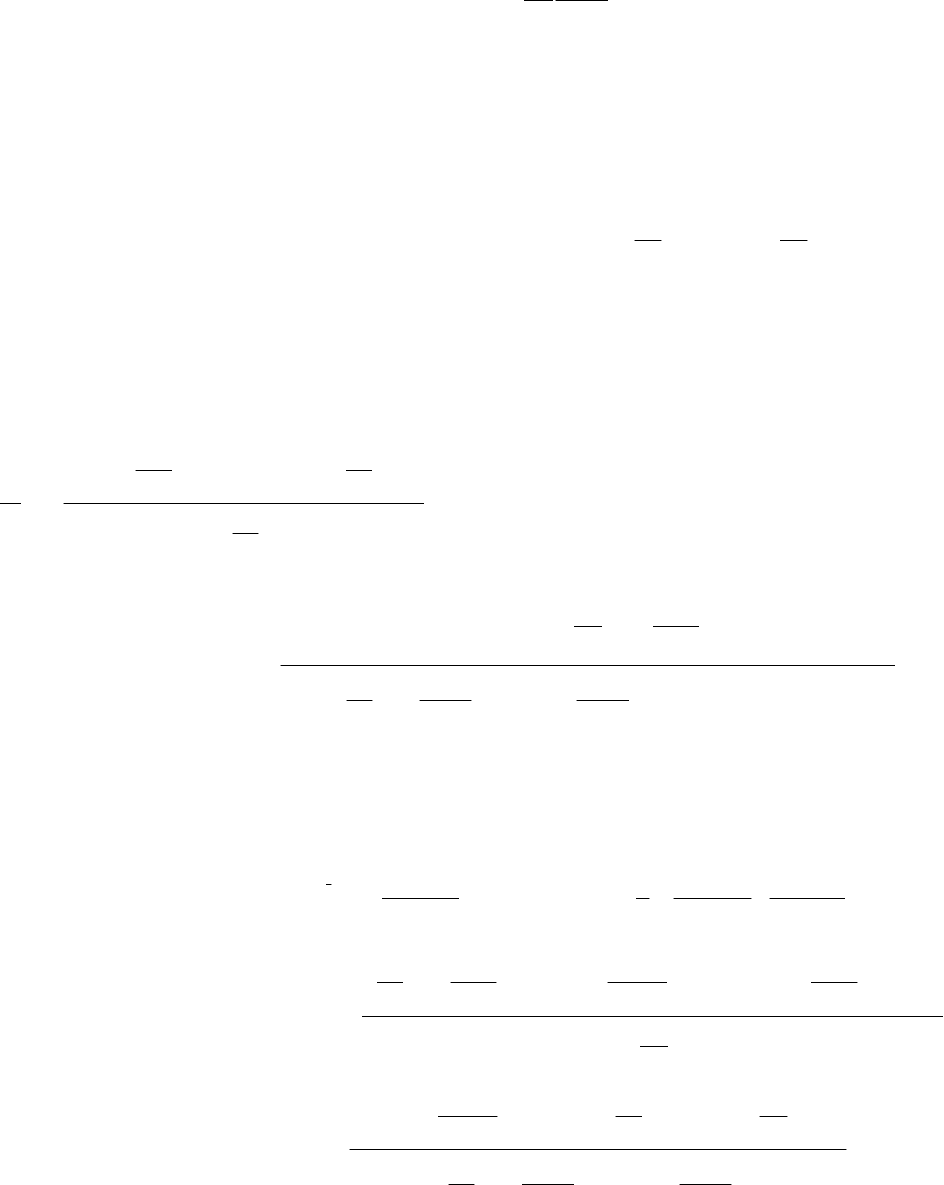
где Q
n
– изображение функции распределенного источника
() ( )
∑
∫
=
−
µρ
ρ
λ
=
N
m
R
R
mnmmm
mm
m
m
m
n
m
m
drrWr
c
q
a
Q
1
2
1
., (9.37)
Решением задачи (9.34) – (9.35) является функция
() ()
()
.exp0,,
2
2
2
n
n
n
n
n
nn
QQ
UU
µ
+τµ−
µ
−µ=τµ
(9.38)
Таким образом, решение исходной задачи (9.1) – (9.5) имеет вид:
()
()
∑
∑
∑
∞
=
=
=
→
×
λ
×
λ
τµ−
ϕ+
µ
++=τ
1
2
,
1
2
1
,
2
2
,,
5,0
expsin
,
n
nm
N
m
m
m
N
m
nm
m
m
nni
i
in
ni
i
i
iii
C
a
С
a
a
r
С
r
B
Art
()
()()()
.
cossincossin
sin
,,,,
,
1
ϕϕ−
ϕ+
µ
ϕ+
µ
µ
−×
ϕ+
µ
−−×
→
∫
−
nmnmnm
m
mn
nm
m
mn
n
m
m
R
R
mnm
m
mn
m
m
mmmm
a
R
a
Ra
R
dr
a
r
r
B
Arfr
m
m
(9.39)
Средняя температура по слоям равна
() ()
()
→
−
ϕ+
µ
ϕ+
µ
µ
−×
×
λ
τµ−
µ
×
ϕ+
µ
+
→
→
×
λ
+
ϕ+
µ
−
ϕ+
µ
−
ϕ+
µ
µ
×
×
−
+
−
−
+=τ
−
=τ
∑
∑
∑
∫
=
−
−
∞
=
=
−
−−
−
−
−
nm
m
mn
nm
m
mn
n
m
m
N
m
nm
m
m
n
n
m
nini
i
in
i
n
nm
N
mm
m
ni
i
in
ini
i
in
ni
i
in
n
m
iiii
ii
iii
R
R
iii
ii
i
a
R
a
Ra
R
С
a
a
С
a
R
R
C
a
a
R
R
a
R
a
Ra
RRRR
RR
BAdrrtr
RR
t
i
i
,,
1
,
2
2
,,
1
1
1
2
,
1
2
,,
1
,
3
1
33
1
3
2
1
2
2
3
1
3
cossin
expcos
5,0
cossinsin
3
2
3
,
3
1

()
()()
.
cossin
sin
,,
,
1
ϕϕ−
ϕ+
µ
−−×
→
∫
−
nmnm
R
R
mnm
m
mn
m
m
mmmm
m
m
dr
a
r
r
B
Arfr
(9.40)
В случае применения данного решения для локальной временной области, интегралы в числителях
правых частей формул (9.39) и (9.40) могут быть вычислены аналитически, так как начальным распре-
делением
()
mm
rf является температурный профиль, определяемый формулой (9.39) для момента време-
ни, соответствующего концу предыдущей области.
Для этого решение (9.39) удобно записать в виде:
()
()
∑
∑
∞
=
=
λ
τµ−
ϕ+
µ
++=τ
1
,
2
,
1
2
2
,,
,
expsin
,
n
nmnm
N
m
m
m
nni
i
in
ni
i
i
iii
ZC
a
a
r
H
r
B
Art
(9.41)
где
()
,sin2
1
,
1
,
2
,,
∫
∑
−
ϕ+
µ
−−
λ
=
=
m
m
R
R
mnm
m
mn
m
m
mmmm
N
m
nm
m
m
nini
dr
a
r
r
B
ArfrС
a
СH
(9.42)
()()
.cossincossin
,,,,,
ϕϕ−
ϕ+
µ
ϕ+
µ
µ
−=
nmnmnm
m
mn
nm
m
mn
n
m
mnm
a
R
a
Ra
RZ
(9.43)
Тогда
()
()
() ()
×−+
ϕ+
µ
−=
=
ϕ+
µ
−−τ=
=
ϕ+
µ
−−=
∫
∫
∫
−
−
−
mmb
R
R
mnm
m
mn
mmmb
R
R
mnm
m
mn
m
m
mbmmbm
R
R
mnm
m
mn
m
m
mmmmnm
BBdr
a
r
rAA
dr
a
r
r
B
Artr
dr
a
r
r
B
ArfrI
m
m
m
m
m
m
1
1
1
,
,
,,
sin
sin,
sin

()
()
×−=
ϕ+
µ
ϕ+
µ
×
×
λ
τµ−
+
ϕ+
µ
×
∫
∑
∑
∫
−
−
∞
=
=
mmb
R
R
mnm
m
mn
kbm
mb
mkb
m
k
kbvkbv
N
vvb
vb
bpkbkbm
R
R
mnm
m
mn
AAdr
a
r
a
r
r
ZC
a
H
dr
a
r
m
m
m
m
1
1
,,
1
,
2
,
1
2
2
,
,
sinsin
exp
sin
×µ−
ϕ+
µ
−
ϕ+
µ
µ
µ
×
−−
− mnnm
m
mn
mnm
m
mn
mn
n
m
R
a
R
a
a
R
R
a
,
1
,
1
1
2
sincos
()
×
µ
−+
ϕ+
µ
−
ϕ+
µ
×
n
m
mbmnm
m
mn
mnm
m
mn
a
BB
a
R
a
a
R
,,
sincos
(
)
×
λ
τµ−
+
ϕ+
µ
−
ϕ+
µ
×
∑
∑
∞
=
=
−
1
,
2
,
1
2
2
,
,,
1
exp
coscos
k
kbvkbv
N
v
bv
bv
bpkbbkm
nm
m
mn
nm
m
mn
ZC
a
H
a
R
a
R
.sinsin
1
,,
∫
−
ϕ+
µ
ϕ+
µ
×
m
m
R
R
mnm
m
mn
kbm
mb
mkb
m
dr
a
r
a
r
r
(9.44)
Интеграл в последнем слагаемом также вычисляется:
