Туголуков Е.Н. Решение задач теплопроводности методом конечных интегральных преобразований
Подождите немного. Документ загружается.


(
)
(
) ()
()
;0;2,1,0;;...,,2,1
;,
,,,
1
,
2
2
2
>τ=≤≤=
τ+
∂
τ∂
+
∂
τ∂
=
τ∂
τ∂
−
kRrRNi
rQ
r
rt
A
r
rt
a
rt
iii
ii
i
ii
ik
i
ii
i
ii
(3.1)
(
)
(
)
;0,
iiii
rfrt
=
(3.2)
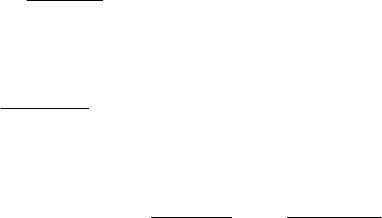
(
)
()()
()
;0,
,
1011
1
01
1
=τ−τα−
∂
τ∂
λ
c
tRt
r
Rt
(3.3)
(
)
()()()
;0,
,
=τ−τα+
∂
τ∂
λ
cNNNN
N
NN
N
tRt
r
Rt
(3.4)
() ()
(
)
(
)
.1...,,2,1
;
,,
;,,
1
1
11
−=
∂
τ
∂
λ=
∂
τ
∂
λτ=τ
+
+
++
Nj
r
Rt
r
Rt
RtRt
j
jj
j
j
jj
jjjjj
(3.5)
Здесь r – пространственная координата; τ – время; N – число слоев многослойной области; t
i
(r
i
, τ) – тем-
пературное поле i-й области; Q
i
(r
i
, τ) – мощность внутреннего источника тепла i-й области; −ρλ
iiii
ca ,,,
2
соответственно теплопроводность, температуропроводность, теплоемкость и плотность вещества i-й
области; A
k, i
– коэффициенты уравнения, определяемые видом координат:
− для декартовой системы координат k = 0, A
0, i
= 0;
− для цилиндрической системы координат k = 1, A
1, i
= 1/r
i
;
− для сферической системы координат k = 2, A
2, i
= 2/ r
i
;
α
1
, α
N
– коэффициенты конвективной теплоотдачи от внешних поверхностей в окружающую среду;
t
c1
(τ), t
cN
(τ) – температуры окружающей среды как функции времени; R
i-1,
R
i
– координаты границ i-й
области.
Для исключения координаты r, вдоль которой свойства тела изменяются ступенчато, используется
формула перехода к изображениям:

() ()( ) ( )
∑
∫
=
µτρ
λ
=τµ
N
m
R
mmmmmm
m
m
m
drrWrtr
a
U
1
0
2
,,,, (3.6)
где
()
−ρ r весовая функция, являющаяся, с точностью до постоянного множителя, решением уравнения
(
)
()
.0
,
=ρ−
ρ
mmk
m
rA
rd
rd
(3.7)
Для декартовой системы координат:
;1)(
=
ρ
r
для цилиндрической системы координат:
;)( rr
=
ρ
для сферической системы координат:
.)(
2
rr =ρ
Ядро интегрального преобразования
(
)
µ
,
mm
rW является решением задачи Штурма – Лиувилля с со-
ответствующими однородными граничными условиями, определяемым с точностью до постоянного
множителя (здесь µ – параметр):
(
)
(
)
()
;,...,,2,1
;0,
,,
1
2
2
,
2
2
mmm
mm
mm
mm
mk
m
mm
RrRNm
rW
ard
rWd
A
rd
rWd
≤≤=
=µ
µ
+
µ
+
µ
−
(3.8)
(
)
()
;0,
,
011
1
01
1
=µα−
µ
λ RW
rd
RWd
(3.9)
(
)
()
;0,
,
=µα+
µ
λ
NNN
N
NN
N
RW
rd
RWd
(3.10)
(
)
(
)
() ()
.1...,,2,1;
,,
;,,
1
1
1
1
−=
µ
λ=
µ
λ
µ=µ
+
+
+
+
Nj
rd
RWd
rd
RWd
RWRW
j
jj
j
j
jj
j
jjjj
(3.11)
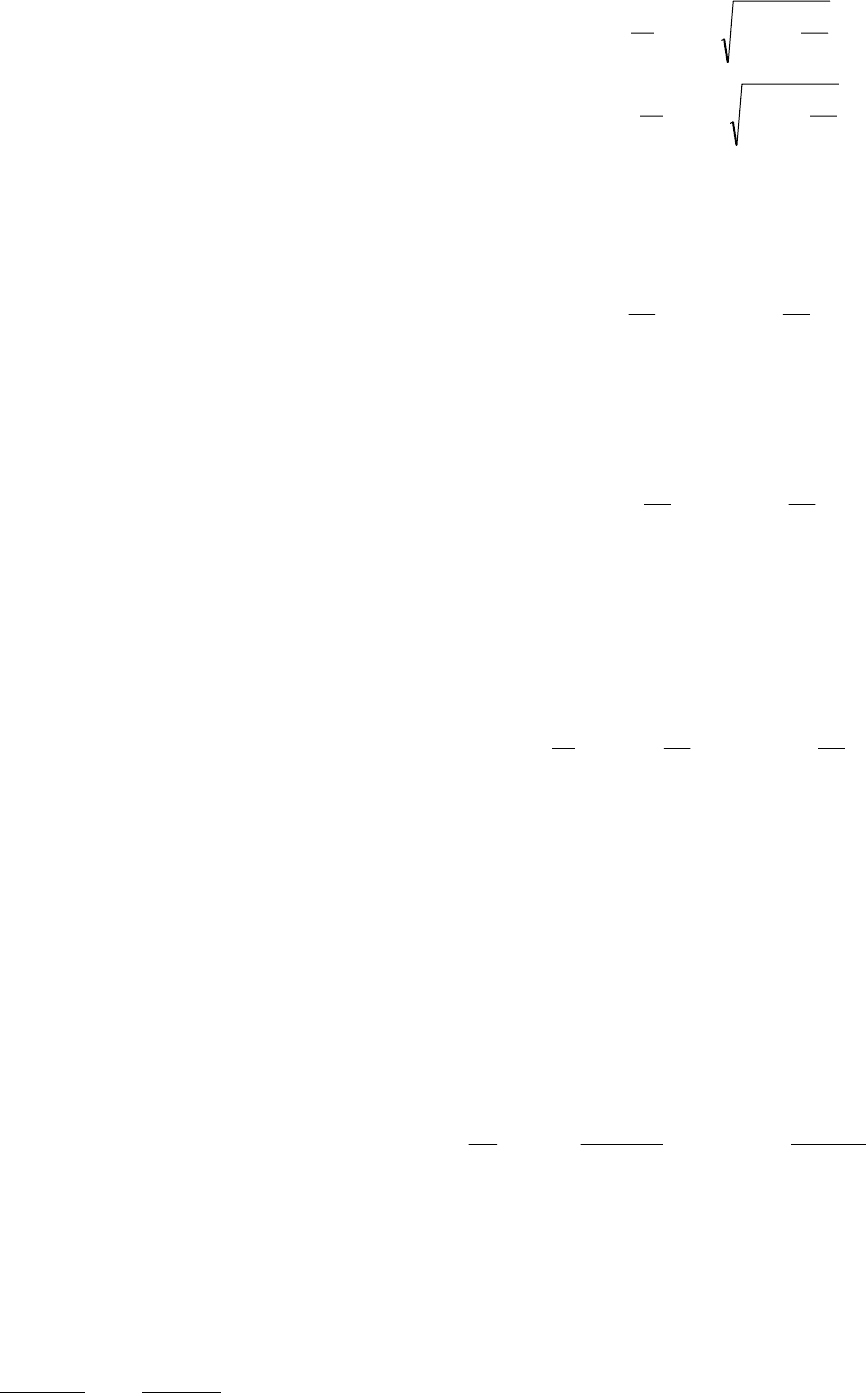
Решение уравнения (3.8) имеет вид:
()
.4
2
еxp2
4
2
еxp1,
2
2
2
,,
2
2
2
,,
µ
−−−+
+
µ
−+−=µ
m
mkmk
m
m
m
mkmk
m
mmm
a
AA
r
C
a
AA
r
CrW
(3.12)
В декартовой системе координат
()
.cos2sin1,
µ
+
µ
=µ
m
m
mm
m
mmm
r
a
Cr
a
CrW (3.13)
В цилиндрической системе координат
()
,21,
00
µ
+
µ
=µ
m
m
mm
m
mmm
r
a
YCr
a
JCrW (3.14)
где
() ()
−zYzJ
00
, функции Бесселя первого рода, нулевого и первого порядка соответственно.
В сферической системе координат
()
.cos2sin1
1
,
µ
+
µ
=µ
m
m
mm
m
m
m
mm
r
a
Cr
a
C
r
rW
(3.15)
Коэффициенты С1
m
и С2
m
, а также числа µ определяются из граничных условий (3.9) – (3.11), при-
чем С1
1
= 1.
Для перехода к изображениям необходимо формулу (3.6) применить почленно к уравнению (3.1) и
начальному условию (3.2).
В общем случае интегралы в правой части (3.6) берутся по частям с учетом граничных условий
(3.3) – (3.5) и (3.9) – (3.11).
Изображение частной производной по времени:
()
()
()
()
.
,
,
,
1
2
1
∑
∫
=
−
τ
τµ
=µ
τ∂
τ∂
ρ
λ
N
m
R
R
mmm
mm
m
m
m
m
m
d
Ud
drrW
rt
r
a
(3.16)
Изображение частных производных по координате. Следующий интеграл берется по частям дваж-
ды:
()
()
()
()
∫
−
=µ
∂
τ∂
+
∂
τ∂
ρ
m
m
R
R
mmm
m
mm
mk
m
mm
m
drrW
r
rt
A
r
rt
r
1
,
,,
,
2
2

()
()
()
()
(
)
()
()
.
,
,,
;
,
,
,,
,
2
2
dudr
dr
rdW
urW
r
rt
rvdvdr
r
rt
A
r
rt
r
m
m
mm
mm
m
mm
mm
m
mm
mk
m
mm
m
=
µ
=µ
∂
τ∂
ρ==
∂
τ∂
+
∂
τ∂
ρ
()
()
() ()
()
()
∫
−
−
=
µ
∂
τ∂
ρ−µ
∂
τ∂
ρ=
m
m
m
m
R
R
m
m
mm
m
mm
m
R
R
mm
m
mm
m
dr
dr
rdW
r
rt
rrW
r
rt
r
1
1
,,
,
,
()
()
()
()
() ()
()
()
.
,,
,
,
;,,
,
2
2
dudr
dr
rdW
r
dr
rdW
rd
rd
u
dr
rdW
r
rtvdvdr
r
rt
m
m
mm
m
m
mm
m
m
m
mm
m
mmm
m
mm
=
µ
ρ+
µρ
=
µ
ρ
τ==
∂
τ∂
()
()
() ()( )
(
)
()( )
() ()
∫
−
−−
=
µ
+
µ
τρ+
+
µ
τρ−µ
∂
τ∂
ρ=
m
m
m
m
m
m
R
R
m
m
mm
mk
m
mm
mmm
R
R
m
mm
mmm
R
R
mm
m
mm
m
dr
dr
rdW
A
dr
rdW
rtr
dr
rdW
rtrrW
r
rt
r
1
11
,,
,
,
,,
,
,
2
2
()
()
() ()( )
()
()( ) ( )
.,,
,
,,
,
1
11
2
2
∫
−
−−
µτρ
µ
−
−
µ
τρ−µ
∂
τ∂
ρ=
m
m
m
m
m
m
R
R
mmmmmm
m
R
R
m
mm
mmm
R
R
mm
m
mm
m
drrWrtr
a
dr
rdW
rtrrW
r
rt
r
(3.17)
()
()
()
()
(()
()
()
() ( )
()
()( ) ( ) )
=µτρ
µ
−
−
µ
τρ−
−µ
∂
τ∂
ρλ=
=µ
∂
τ∂
+
∂
τ∂
ρ
λ
∫
∑
∫
∑
−
−
−
−
=
=
m
m
m
m
m
m
m
m
R
R
mmmmmm
m
R
R
m
mm
mmm
R
R
mm
m
mm
m
N
m
m
R
R
mmm
m
mm
mk
m
mm
mm
N
m
m
m
drrWrtr
a
dr
rdW
rtr
rW
r
rt
r
drrW
r
rt
A
r
rt
ar
a
1
1
1
1
,,
,
,
,
,
,
,,
2
2
1
,
2
2
2
1
2
()
()
()()
()
()
()
()()
()
()
=τµµ−
µ
τ−µ
∂
τ∂
ρλ−
−
µ
τ−µ
∂
τ∂
ρλ=
,
,
,,
,
,
,,
,
2
1
01
0101
1
01
01
U
dr
RdW
RtRW
r
Rt
R
dr
RdW
RtRW
r
Rt
R
N
NN
NNNN
N
NN
NN
()( )() ()( )
(
)
(
)
.,,,
2
1001
τµµ−τµρα+τµρα= UtRWRtRWR
cNcNNN
(3.18)
Изображение начального условия:

() () ( )
.,
0
1
2
1
UdrrWrfr
a
N
m
R
R
mmmmmm
m
m
m
m
=µρ
λ
∑
∫
=
−
(3.19)
Изображение функции источника:
()
()
() ()
.,,
,
1
2
1
τµ=µ
ρ
τ
ρ
λ
∑
∫
=
−
GdrrW
c
rQ
r
a
N
m
R
R
mmm
mm
mm
m
m
m
m
m
(3.20)
Таким образом, в изображениях имеем задачу:
(
)
()() ()( )()
() ( )()
;,
,,,
,
1001
2
τµρα+
+τµρα+τµ=τµµ+
τ
τµ
cn
NcnNNNnnn
n
tRWR
tRWRGU
d
Ud
(3.21)
(
)
.0,
0
UU
n
=
µ
(3.22)
Решение задачи (3.21) – (3.22) в изображениях имеет вид:
(
)
(
)
() () ( )()
()
,еxp,,0,
еxp,
0
2
2
ττµτµ+τµ+µ×
×τµ−=τµ
∫
τ
dFWGU
U
nnnn
nn
(3.23)
где
(
)
(
)
(
)()
()( )()
.,
,,
1001
τµρα+
+τ
µ
ρ
α
=
τ
µ
cn
NcnNNNn
tRWR
tRWRFW
(3.24)
Обратный переход осуществляется по формуле:
()
(
)( )
,
,,
,
1
∑
∞
=
µτµ
=τ
n
n
nmmn
mm
S
rWU
rt
(3.25)
где
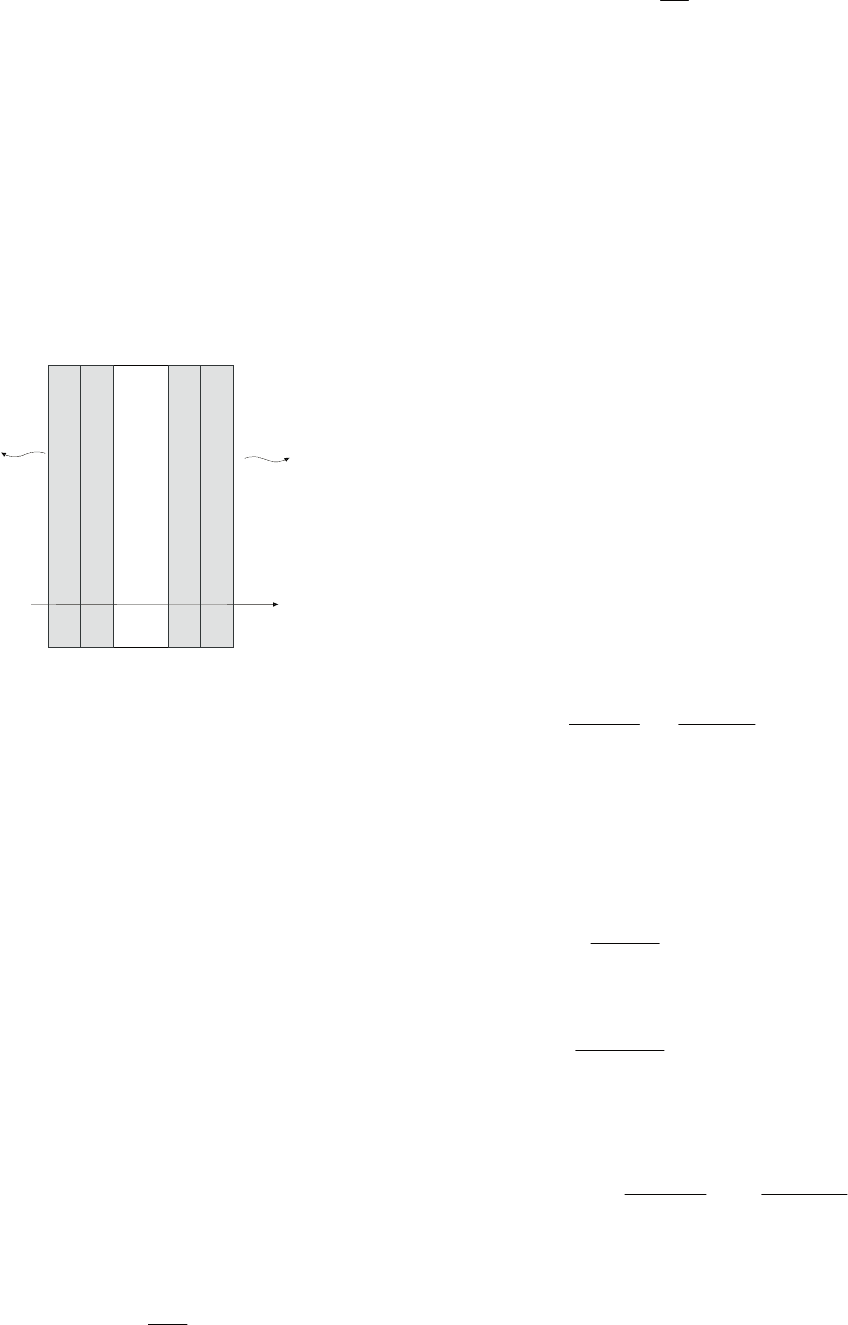
() ( )
.,
1
2
2
1
∫
∑
−
µρ
λ
=
=
m
m
R
R
mnmmm
m
m
N
m
n
drrWr
a
S (3.26)
4 РЕШЕНИЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ ДЛЯ N-СЛОЙНОЙ
НЕОГРАНИЧЕННОЙ ПЛАСТИНЫ
Решение нестационарной задачи теплопроводности для N-слойной неограниченной пластины (рис.
4.1) с произвольным начальным распределением, граничными условиями
4-го рода на поверхностях контакта слоев и неоднородными несиммет-
ричными граничными условиями 3-го рода на внешних границах приве-
дено ниже.
Решение задачи может быть использовано для расчета нестационар-
ных температурных полей и тепловых потоков в многослойных листовых
изделиях, плоских элементах аппаратов, конструкций и сооружений, в
плоских образцах, у которых теплофизические параметры функциональ-
но зависят от температуры, а также для определения условий протекания
теплообменных процессов в перечисленных выше случаях по измерен-
ным температурным полям.
(
)
(
)
;0,0,...,,2,1
,
,,
2
2
2
>τ≤≤=
∂
τ∂
=
τ∂
τ∂
ii
i
ii
i
ii
RxNi
x
xt
a
xt
(4.1)
(
)
(
)
;0,
iiii
xfxt
=
(4.2)
(
)
()()
;0,0
,0
111
1
1
1
=−τα−
∂
τ∂
λ
c
tt
x
t
(4.3)
(
)
()()
;0,
,
=−τα+
∂
τ∂
λ
cNNNN
N
NN
N
tRt
x
Rt
(4.4)
(
)
(
)
()
()
.1...,,2,1
,
,0,
;,0,
1
1
1
1
−=
∂
τ∂
λ=
∂
τ∂
λ
τ=τ
+
+
+
+
Nj
x
t
x
Rt
tRt
j
j
j
j
jj
j
jjj
(4.5)
Здесь
ii
i
i
c
a
ρ
λ
=
2
– коэффициенты температуропроводности слоев.
Решение задачи (4.1) – (4.5) с неоднородными граничными условиями может быть получено непо-
средственным применением метода конечных интегральных преобразований, но, поскольку решение
предполагается для использования в компьютерных расчетах, для улучшения сходимости рядов, обра-
зующих решение, целесообразно выделить стационарную составляющую. Тогда решение представляет-
…
α
1
α
N
t
c1
t
cN
х
0
R
R
R
R
.
. . . .
λ
N
λ
1
λ
2
λ
N
-1
c
N
c
1
c
2
c
ρ
ρ
1
ρ
2
ρ
N
-1
N
-1
N
N
N
-1
2 1
Рис. 4.1 N-слойная
неограниченная пластина
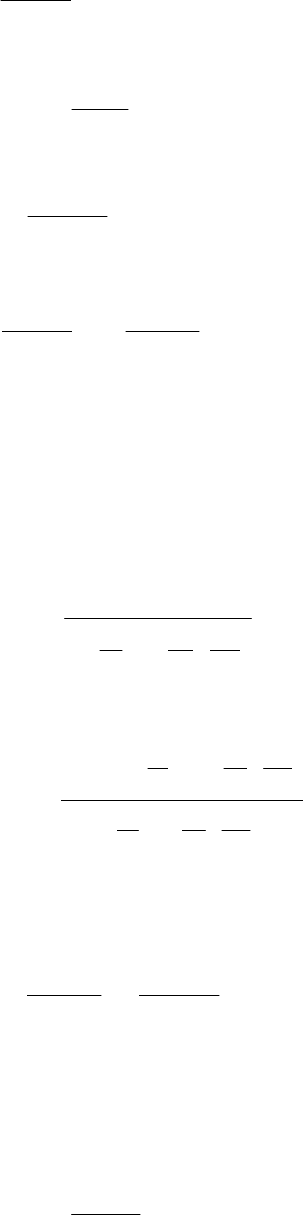
ся в виде:
(
)
(
)
(
)
,...,,2,1,,, NixPxSxt
iiiiii
=
τ
+
=
τ
(4.6)
где
()
−
ii
xS решение стационарной задачи с неоднородными граничными условиями
(
)
;0,...,,2,1,0
2
2
ii
i
ii
RxNi
xd
xSd
≤≤==
(4.7)
(
)
()()
;00
0
111
1
1
1
=−α−λ
c
tS
xd
Sd
(4.8)
(
)
()()
;0=−α+λ
cNNNN
N
NN
N
tRS
xd
RSd
(4.9)
(
)
(
)
()
()
.1...,,2,1,
0
;0
1
1
1
1
−=λ=λ
=
+
+
+
+
Nj
xd
Sd
xd
RSd
SRS
j
j
j
j
jj
j
jjj
(4.10)
Решение стационарной задачи (4.7) – (4.10) имеет вид:
(
)
,
iiiii
BxAxS
+
=
(4.11)
где
;
11
1
1
1
α
+
λ
+
α
λ
−
=
∑
=
N
k
Nk
k
i
ccN
i
R
tt
A
(4.12)
()
.
11
1
1
1
1
1
∑
∑
=
+=
α
+
λ
+
α
α
+
λ
+
λ
−
−=
N
k
Nk
k
N
ik
Nk
k
i
i
ccN
cNi
R
RR
tt
tB
(4.13)
()
−τ,
ii
xP решение нестационарной задачи с однородными граничными условиями:
(
)
(
)
;0,0,...,,2,1
,
,,
2
2
2
>τ≤≤=
∂
τ∂
=
τ∂
τ∂
ii
i
ii
i
ii
RxNi
x
xP
a
xP
(4.14)
(
)
(
)()
;0,
iiiiii
xSxfxP −
=
(4.15)
(
)
()
;0,0
,0
11
1
1
1
=τα−
∂
τ∂
λ P
x
P
(4.16)

(
)
()
;0,
,
=τα+
∂
τ∂
λ
NNN
N
NN
N
RP
x
RP
(4.17)
(
)
(
)
()
()
.1...,,2,1,
,0,
;,0,
1
1
1
1
−=
∂
τ∂
λ=
∂
τ∂
λ
τ=τ
+
+
+
+
Nj
x
P
x
RP
PRP
j
j
j
j
jj
j
jjj
(4.18)
Решение задачи (4.14) – (4.18) получено методом конечных интегральных преобразований. Для ис-
ключения координаты х, вдоль которой свойства тела изменяются ступенчато, используется формула
перехода к изображениям:
() ()( )
.,,,
1
0
2
∑
∫
=
µτ
λ
=τµ
N
m
R
mmmmm
m
m
m
dxxWxP
a
U (4.19)
Весовая функция, равная 1, опущена.
Обратный переход осуществляется по формуле:
()
(
)( )
,
,,
,
1
∑
∞
=
µτµ
=τ
n
n
niin
ii
Z
xWU
xP
(4.20)
где
()
−
ϕ+
µ
ϕ+
µ
µ
−×
×
λ
=µ
λ
=
∑
∫
∑
==
nm
m
mn
nm
m
mn
n
m
m
nm
N
m
m
m
R
mnmm
m
m
N
m
n
a
R
a
Ra
R
C
a
dxxW
a
Z
m
,,
2
,
1
2
0
2
2
1
cossin
5,0,
()()
,cossin
,,
ϕϕ−
nmnm
(4.21)
а ядро интегрального преобразования
()
µ
,
mm
xW является решением вспомогательной задачи (здесь µ –
параметр):
(
)
()
,0,
,
2
2
2
2
=µ
µ
+
µ
mm
mm
mm
xW
axd
xWd
;0,...,,2,1
mm
RxNm ≤
≤
=
(4.22)
(
)
()
;0,0
,0
11
1
1
1
=µα−
µ
λ W
xd
Wd
(4.23)
(
)
()
;0,
,
=µα+
µ
λ
NNN
N
NN
N
RW
xd
RWd
(4.24)
(
)
()
;,0,
1
µ=µ
+jjj
WRW
(
)
(
)
1...,,2,1,
,0,
1
1
1
−=
µ
λ=
µ
λ
+
+
+
Nj
xd
Wd
xd
RWd
j
j
j
j
jj
j
. (4.25)
Подставляя решение задачи (4.22)
()
ϕ+
µ
=µ
nm
m
mn
nmnmm
a
x
СxW
,,
sin, (4.26)
в граничные условия (4.23) – (4.25), находим числа
nnmnm
C µϕ ,,
,,
, причем
n
C
,1
принимаются равными 1:
;arctg
11
1
,1
α
µλ
=ϕ
a
n
n
(4.27)
,tgarctg
,
1
1
,1
ϕ+
µ
λ
λ
=ϕ
+
+
+ nj
j
jn
jj
jj
nj
a
R
a
a
;1...,,2,1
−
=
Nj (4.28)
()
;
sin
sin
,1
,
,,1
nj
nj
j
jn
njnj
a
R
CC
+
+
ϕ
ϕ+
µ
=
(4.29)
−µ
n
n-й положительный корень уравнения
