Туголуков Е.Н. Решение задач теплопроводности методом конечных интегральных преобразований
Подождите немного. Документ загружается.


Рассмотрим задачу с однородными граничными условиями для случая, когда теплопроводность сре-
ды, в которой протекает тепловой процесс, может быть представлена как функция пространственных ко-
ординат.
(
)
()
(
)
;0,0,
,,
>τ≤≤
∂
τ∂
λ
∂
∂
=
τ∂
τ∂
ρ Rx
x
xt
x
x
xt
c
(15.15)
(
)
(
)
;0, xfxt
=
(15.16)
()
(
)
()
;0,0
,0
0
1
=τα−
∂
τ∂
λ t
x
t
(15.17)
()
(
)
()
.0,
,
2
=τα+
∂
τ∂
λ Rt
x
Rt
R
(15.18)
Формула перехода к изображениям:
() ()()
.,,,
0
∫
µτ=τµ
R
dxxWxtU
(15.19)
Весовая функция, равная 1, опущена.
Обратный переход осуществляется по формуле:
()
(
)( )
,
,,
,
1
∑
∞
=
µτµ
=τ
n
n
nn
Z
xWU
xt
(15.20)
где
()
∫
µ=
R
n
dxxWZ
0
2
., (15.21)
Ядро интегрального преобразования
(
)
µ
,xW является решением вспомогательной задачи (здесь µ –
параметр):
()
(
)
()
;0,0,
,
2
RxxW
dx
xdW
x
dx
d
≤≤=µµ+
µ
λ
(15.22)

()
(
)
()
;0,0
,0
0
1
=µα−
µ
λ W
dx
dW
(15.23)
()
(
)
()
.0,
,
2
=µα+
µ
λ RW
dx
RdW
R
(15.24)
Рассмотрим случай, когда
(
)
.bkxx
+
=
λ
(15.25)
Тогда
(
)
.0
2
=µ+
′
+
′′
+ WWkWbkx
(15.26)
С точностью до постоянного множителя
()
.22,
00
+
µ
+
+
µ
=µ bkx
k
CYbkx
k
JxW
(15.27)
(
)
.22
,
11
+
µ
+
+
µ
+
µ
−=
µ
bkx
k
CYbkx
k
J
bkx
dx
xdW
(15.28)
С и µ определяются из граничных условий (15.23), (15.24):
;
22
22
101
101
µµ
+
µ
α
µµ
−
µ
α
=
b
k
Y
b
b
k
Y
b
k
J
b
b
k
J
С
(15.29)
µ – последовательные положительные корни уравнения
−
+
µ
+
+
µ
α bkR
k
CYbkR
k
J 22
002
.022
11
=
+
µ
+
+
µ
+µ− bkR
k
YCbkR
k
JbkR
(15.30)

Применяя преобразование (15.19) к задаче (15.15) – (15.18), переходим к изображениям:
(
)
()
;0,
,
2
=τµµ+
τ
τµ
ρ
nn
n
U
d
dU
c (15.31)
() ()()
∫
µ=µ
R
nn
dxxWxfU
0
.,0,
(15.32)
Решением задачи (15.31) – (15.32) является функция
()()
.exp0,,
2
τ
ρ
µ
−µ=τµ
c
UU
n
nn
(15.33)
Теперь рассмотрим задачу с однородными граничными условиями для случая, когда теплопровод-
ность среды, в которой протекает тепловой процесс, может быть представлена как функция температу-
ры.
(
)
()()
(
)
;0;0;
,
,
,
>τ≤≤
∂
τ∂
τλ
∂
∂
=
τ∂
τ∂
ρ Rx
x
xt
xt
x
xt
c
(15.34)
(
)
(
)
;0, xxt
ϕ
=
(15.35)
()()
(
)
()
;0,0
,0
,0
0
=τα−
∂
τ∂
τλ t
x
t
t
(15.36)
()()
(
)
()
.0,
,
, =τα+
∂
τ∂
τλ Rt
x
Rt
Rt
R
(15.37)
Здесь х – пространственная координата; τ – время; t (х, τ) – температурное поле;
()
−λ t
коэффициент
теплопроводности, являющийся функцией температуры; с, ρ – соответственно теплоемкость и плот-
ность вещества; α
0
, α
R
– коэффициенты конвективной теплоотдачи от внешних поверхностей в окру-
жающую среду; R – координата границы области.
Для исключения пространственной координаты х используется стандартная формула перехода к
изображениям:
() ()()
∫
µτ=τµ
R
dxxwxtu
0
,,, (15.38)

с формулой обратного перехода
()
(
)( )
.
,,
,
1
∑
∞
=
µτµ
=τ
n
n
nn
s
xwu
xt
(15.39)
Ядро интегрального преобразования
(
)
µ
,xw является решением задачи, определяемым с точностью
до постоянного множителя (здесь µ – параметр):
()()
(
)
()
;0,0
2
Rxxw
dx
xdw
xw
dx
d
≤≤=µ+
λ
(15.40)
()()
(
)
()
;00
0
0
0
=α−λ w
dx
dw
w
(15.41)
()()
(
)
()
.0=α+λ Rw
dx
Rdw
Rw
R
(15.42)
Уравнение (15.40) является дифференциальным уравнением вида
()
(
)
,0
2
=µ+λ www
I
I
(15.43)
или
(
)
(
)
.0''"
22
=µ+λ+λ wwwww
(15.44)
Пусть
(
)
(
)
.'
2
xwwp = (15.45)
Тогда
(
)
(
)
,0'
=
+
+
wHpwGp (15.46)
где
()
(
)
()
()
()
.2;
'
2
2
w
w
wH
w
w
wG
λ
µ
=
λ
λ
=
(15.47)

Решение этого уравнения имеет вид:
() ( ) () ()
,expexp
−η−=
∫
ξ
w
dwFwHFwp (15.48)
где
() () ()
., η=ξ=
∫
ξ
pdwwGwF
w
(15.49)
()
∫
µ=
R
nn
dxxws
0
2
., (15.50)
В изображениях задача имеет простой вид:
(
)
()
,0,
,
2
=τµµ+
τ∂
τµ∂
ρ u
u
c
(15.51)
() ()()
∫
µϕ=µ
R
nn
dxxwxu
0
.,0,
(15.52)
15.2 Об использовании конечно-разностного аналога для
приближенного решения нестационарной задачи теплопроводности
Другой подход к решению нелинейной задачи теплопроводности может быть основан на дискрети-
зации временной координаты и использовании конечно-разностного аналога частной производной тем-
пературы по времени.
Рассмотрим нелинейное неоднородное уравнение теплопроводности
(
)
()
(
)
()
τ+
∂
τ∂
∂
∂
=
τ∂
τ∂
,
,,
xu
x
xt
xa
x
xt
(15.53)
с произвольным начальным условием (15.35) и однородными граничными условиями:
()
(
)
()
;0,0
,0
0
0
=τα−
∂
τ∂
λ t
x
t
(15.54)
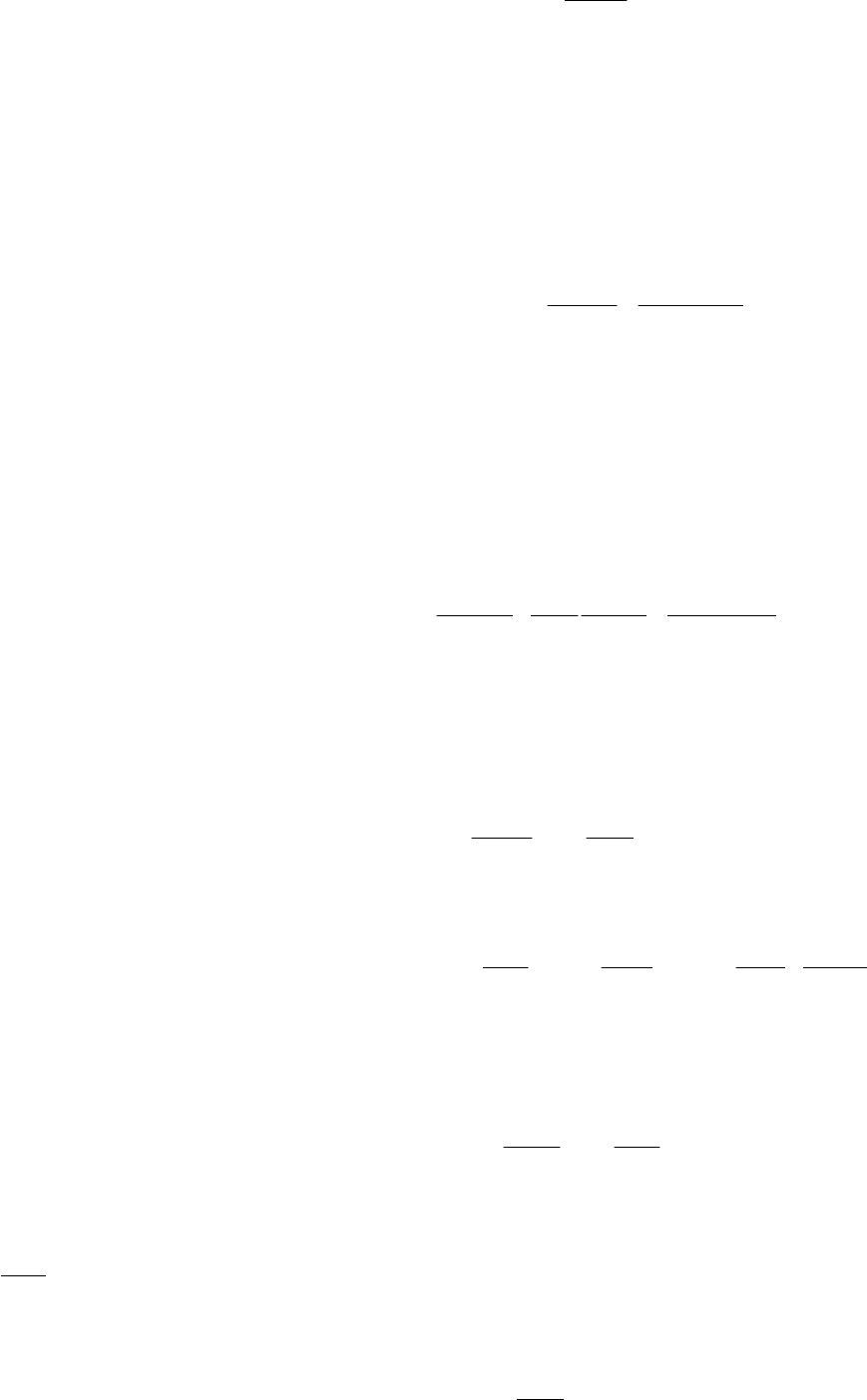
()
(
)
()
.0,
,
=τα+
∂
τ∂
λ Rt
x
Rt
R
R
(15.55)
Интервал времени [0, T ] разделим на n равных частей точками ,/;...,,2,1; nThnihi
i
=
=
=
τ
и поло-
жим
()()
., xtxt
ii
=τ
Производную по времени заменим конечно-разностным аналогом:
(
)
(
)()
h
xtxt
xt
ii
i
−
≈
τ∂
τ∂
+1
,
. (15.56)
В результате получим систему обыкновенных дифференциальных уравнений для функций
(
)
xt
i
, ко-
торые являются приближенными значениями функции
(
)
.,
i
xt
τ
Эта система уравнений имеет вид:
()
(
)
()
(
) () ()
()
.,
1
11
2
1
2
+
+++
τ−
−
=
∂
∂
+
i
iiii
xu
h
xtxt
dx
xdt
x
xa
dx
xtd
xa (15.57)
Рассмотрим уравнение
(
)
()
(
)
() () ()
,
2
2
xxyx
dx
xdy
x
dx
xyd
θ=ω−χ+ (15.58)
где
()
(
)
()
()
()
()
()
()
()
()
.
,
;
1
;
'
xa
xu
hxa
xt
x
hxa
x
xa
xa
x
ii
τ
−−=θ=ω=χ
(15.59)
Однородное уравнение
(
)
()
(
)
()()
0
2
2
=ξω−
ξ
χ+
ξ
xx
dx
xd
x
dx
xd
(15.60)
заменой
()
() ()
xvx
dx
xd
ξ=
ξ
сводится к уравнению Риккарти
(
)
() () () ()
.
2
xxvxxv
dx
xdv
ω=χ++
(15.61)

Оно имеет точные решения для ряда функций
(
)
x
ω
, которыми может быть аппроксимирована функ-
ция
()
.
1
hxa
Тогда
() ( ) ()
,exp
0
0
ξ=ξ
∫
x
x
dxxvxx (15.62)
а функция y (x) выражается через фундаментальную систему решений ξ
1
(х) и ξ
2
(х):
() ()
(
)
(
)
()
()
(
)
(
)
()
() ()
,
2211
2
1
1
2
xCxCdx
xW
xx
xdx
xW
xx
xxy ξ+ξ+
θξ
ξ−
θξ
ξ=
∫∫
(15.63)
где
() ()
(
)
()
()
.
1
2
2
1
xd
xd
x
xd
xd
xxW
ξ
ξ−
ξ
ξ=
(15.64)
Таким образом, расчет нестационарного температурного поля выполняется последовательно для
моментов времени τ
i
, i = 1, 2, …, n по решению задачи (15.58) с начальным условием, соответствую-
щим температурному полю в конце предыдущего временного интервала. Для первого интервала ис-
пользуется начальное распределение исходной задачи.
16 РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ
При математическом моделировании температурных полей, как правило, основным источником по-
грешностей служат значения конвективных коэффициентов теплоотдачи, входящие в граничные усло-
вия третьего рода задачи теплопроводности.
Коэффициент теплоотдачи является комплексной характеристикой интенсивности теплообмена те-
плоотдающей (тепловоспринимающей) поверхности и омывающего ее потока жидкости (газа). Он зави-
сит от большого количества физических, геометрических и режимных параметров теплообменного про-
цесса (10 и более). Поэтому вывод прямых аналитических зависимостей для расчета коэффициентов
конвективной теплоотдачи на основе фундаментальных знаний о природе процессов теплопереноса в
пространстве не представляется возможным.
Существуют различные возможности для определения численных значений коэффициентов кон-
вективной теплоотдачи в конкретных условиях протекания теплообменного процесса.
Классическая инженерная методика расчета коэффициентов конвективной теплоотдачи, базирую-
щаяся на теории подобия, основана на использовании критериальных уравнений алгебраического типа,
обобщающих экспериментальные данные по различным веществам, выступающим в роли теплоносите-
лей, для каждого набора условий протекания теплообменного процесса. Поэтому использование крите-
риальных уравнений, являющихся по сути результатом многомерной аппроксимации, приводит в каж-
дом конкретном расчете к погрешностям, не поддающимся оценке. Как правило, погрешность расчета

коэффициентов конвективной теплоотдачи по критериальным уравнениям составляет не менее
30…50 %.
Другой путь связан с непосредственным измерением температурных полей в лабораторных или
промышленных условиях на действующем оборудовании для исследуемых условий протекания тепло-
обменных процессов и видов теплоносителей. По результатам измерений температурных полей могут
быть вычислены локальные значения коэффициентов теплоотдачи.
Возможно аналитическое определение коэффициента теплоотдачи по результатам эксперименталь-
ных исследований путем решения обратной задачи теплопроводности.
В качестве иллюстрации такого подхода (для декартовых координат) рассмотрим процесс конвек-
тивного теплообмена плоской неограниченной пластины с окружающей средой, имеющей постоянную
температуру.
Пусть измеряется температура во времени в ряде точек по толщине пластины. Температурное поле
такой пластины описывается решением следующей задачей теплопроводности:
(
)
(
)
,0,0,
,,
2
2
≥τ≤≤
∂
τ∂
=
τ∂
τ∂
Rx
x
xt
a
xt
(16.1)
с начальным условием
(
)
сonst0,
0
=
=
txt , (16.2)
и граничными условиями
(
)
()()
0,
,
=−τα+
∂
τ∂
λ
c
tRt
x
Rt
, (16.3)
(
)
0
,0
=
∂
τ∂
x
t
. (16.4)
Здесь х – координата, направленная по нормали к поверхности пластины; τ – время; t (x, τ) – темпе-
ратурное поле пластины; −
ρ
λ
=
c
a коэффициент температуропроводности материала пластины;
−ρλ ,,с теплопроводность, теплоемкость и плотность материала пластины соответственно; t
0
– начальная
температура пластины; t
с
– температура окружающей среды; R – полутолщина пластины; α –
коэффициент теплоотдачи.
Введем замену переменной
(
)
(
)
с
txtxT
−
τ
=
τ
,, , (16.5)

позволяющую перейти к задаче с однородными граничными условиями:
(
)
(
)
2
2
,,
x
xT
a
xT
∂
τ∂
=
τ∂
τ∂
, (16.6)
(
)
c
ttТxT
−
=
=
00
0, , (16.7)
(
)
()
0,
,
=τα+
∂
τ∂
λ RT
x
RT
, (16.8)
(
)
0
,0
=
∂
τ∂
x
T
. (16.9)
Применим к этой задаче конечное интегральное преобразование
() ( ) ()
∫
ρτ=τ
R
dxxSxTW
0
, , (16.10)
причем весовая функция ρ = 1, а функция S(х), являющаяся ядром интегрального преобразования, опре-
деляется как решение вспомогательной задачи Штурма–Лиувилля:
(
)
()
0
2
2
2
=µ+ xS
dx
xSd
; (16.11)
(
)
()
0=α+λ RS
dx
RdS
; (16.12)
(
)
0
0
=
dx
dS
. (16.13)
Решение этой задачи с точностью до постоянного множителя имеет вид:
(
)
(
)
ϕ
+
µ
=
xxS sin . (16.14)
Тогда
(
)
()
ϕ+µµ= x
dx
xdS
cos
. (16.15)

Из граничного условия (16.13)
(
)
0cos
=
ϕ
µ
, (16.16)
откуда (минимальный положительный корень)
2
π
=ϕ
(16.17)
следовательно:
(
)
(
)
xxS
µ
=
cos . (16.18)
Из граничного условия (16.12) имеем:
(
)
(
)
0cossin =
µ
α
+
µ
µ
λ
−
RR , (16.19)
откуда в конечном итоге и определяется искомый коэффициент теплоотдачи:
(
)
R
µ
µ
λ
=
α
tg . (16.20)
Выполняем переход к изображениям:
(
)
()
0
2
=τµ+
τ
τ
Wa
d
dW
; (16.21)
изображение начального условия (16.7):
() ( ) ()
∫
µ
µ
=µ=
R
R
T
dxxTW
0
0
0
sincos0
. (16.22)
Решение задачи (16.21) – (16.22) в изображениях:
