Туголуков Е.Н. Решение задач теплопроводности методом конечных интегральных преобразований
Подождите немного. Документ загружается.

где R
1
и R
2
– соответственно внутренний и наружный радиусы трубы.
Обозначив
(
)
()
()
()
,
2
;
2
2
1
2
2
222111
2
1
2
2
2211
ρ−
α+α
=
ρ−
α+α
=
RRc
tRtR
S
RRc
RR
K
(13.8)
имеем для уравнения (13.6) решение вида (13.5).
14 ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПЕРЕНОСА
ТЕПЛА ЖИДКОСТЬЮ, ДВИЖУЩЕЙСЯ В РЕЖИМЕ
ИДЕАЛЬНОГО ВЫТЕСНЕНИЯ ПО КАНАЛУ С УЧЕТОМ
ПЕРЕНОСА ТЕПЛА ТЕПЛОПРОВОДНОСТЬЮ
Приводятся вывод и решение нестационарного уравнения переноса тепла жидкостью, движущейся
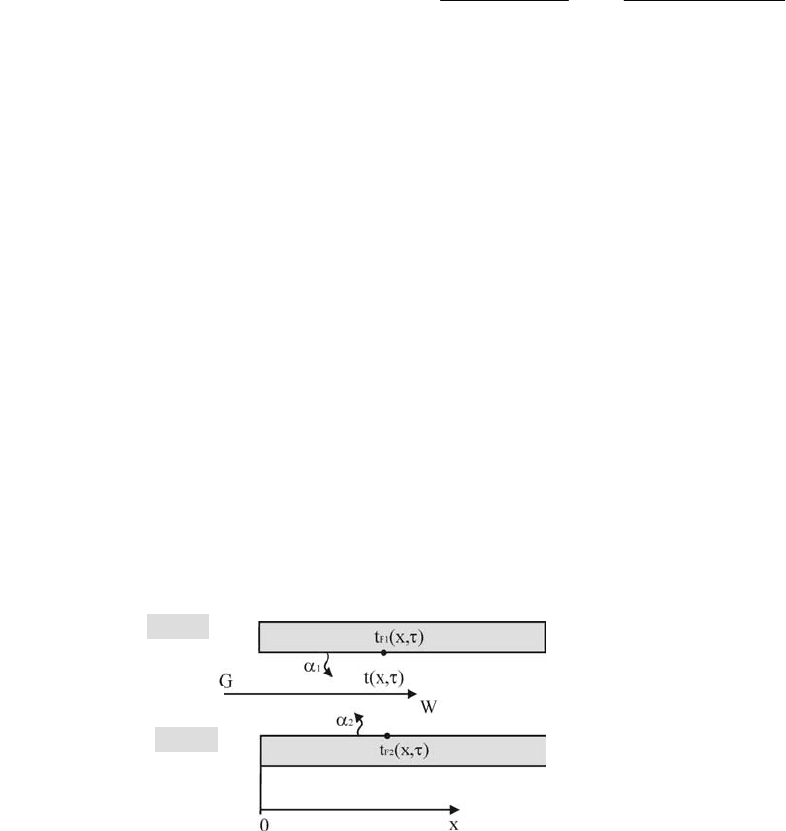
в режиме идеального вытеснения по каналу, образованному N поверхностями (рис. 14.1), температуры
которых меняются по длине канала и во времени. Учитываются конвективная и молекулярная состав-
ляющие тепловых потоков.
Рассмотрим случай, когда движущаяся жидкость омывает стенки канала, образованные N различ-
ными поверхностями с разными температурами. Частными случаями являются движение теплоносителя
по кольцевому каналу рубашки емкостного аппарата или по межтрубному пространству кожухотрубча-
того аппарата.
Рис. 14.1 Схема канала, образованного двумя поверхностями
с различными температурами
Возможно использование приводимой методики и полученных уравнений для математического мо-
делирования температурного поля жидкости, движущейся по каналу, заполненному насыпным слоем
твердых гранул сорбента или катализатора при наличии теплообмена как с гранулами, так и со стенка-
ми канала.
При выводе уравнения используются следующие допущения:
− температура жидкости по сечению канала не меняется;
− жидкость несжимаемая;
− теплофизические характеристики жидкости не зависят от температуры;
− канал имеет постоянное сечение.
G
W
x
0
α
1
α
2
t
(
x
τ
)
t
F
1
(
x
τ
)
t
F
2
(
x
τ
)

Приняты следующие обозначения:
х – пространственная координата по направлению движения потока;
τ – время;
t (x, τ) – текущая температура жидкости;
G – массовый расход жидкости;
с – теплоемкость жидкости;
q
i
– плотность теплового потока через стенку i-го канала;
∆F
i
= П
i
∆х – площадь i-й стенки канала элементарной области;
П
i
– омываемый периметр i-й стенки канала;
α
i
– коэффициент конвективной теплоотдачи от i-й стенки канала к жидкости;
t
Fi
(x, τ) – температура i-й стенки канала.
Выделим элементарную область длиной ∆х по направлению движения потока.
Запишем составляющие теплового баланса для элементарной области.
Тепло, привносимое потоком жидкости за время ∆τ
()
(
)
;
,
, Sd
x
xt
dxtcGQ
p
τ
∂
τ∂
λ−ττ=
(14.1)
тепло, уносимое потоком жидкости за время ∆τ
()
(
)
Sd
x
dxxt
ddхxGctQ
u
τ
∂
τ+∂
λ−ττ+=
,
,
; (14.2)
тепло, отдаваемое элементарной области i-й поверхностью
(
)()
(
)
;,, ττ−τα== ddFxtxtdFqQ
iFiiiii
(14.3)
теплота, привносимая дополнительными источниками тепла
,
τ
=
ddxSqQ
dd
(14.4)
где q
d
– удельная мощность дополнительных источников тепла; S – площадь сечения канала.
Изменение теплосодержания жидкости в элементарной области за время dτ:
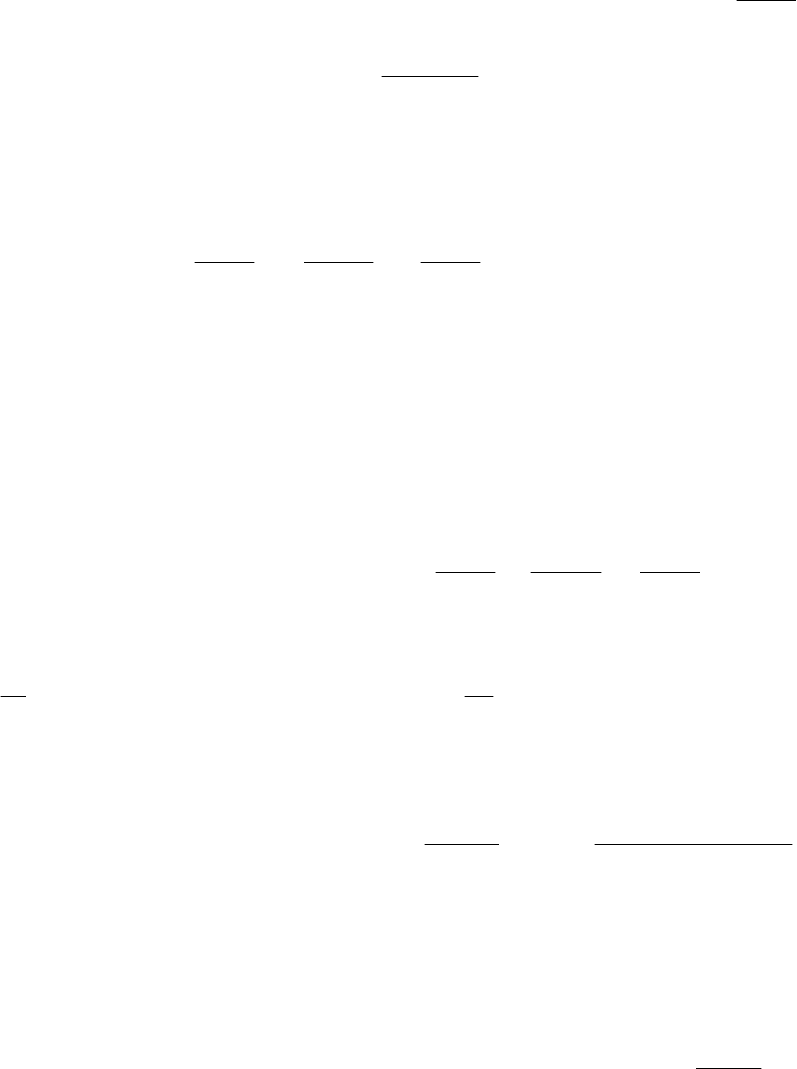
(
)()
(
)
,,, τ
−
τ
+
τ
ρ
=
xtdxtcSdxQ (14.5)
где ρ – плотность жидкости.
Изменение теплосодержания жидкости обусловлено результирующим количеством тепла, подве-
денным к жидкости в элементарной области:
∑
++=
i
iup
QQQQ
(14.6)
или
()()()()
()
()
+ττ+−τ
∂
τ∂
λ−ττ=τ−τ+τρ ddхxtcGSd
x
xt
dxtcGxtdxtcdxS ,
,
,,,
(
)
()()()
∑
ττ−τα+τ+τ
∂
τ+∂
λ+
i
iFiid
ddxxtxtddxSqSd
x
dxxt
.П,,
,
(14.7)
Разделив уравнение почленно на произведение
τ
ddx
и выполнив предельные переходы, получим:
() ()
(
)
()()()
∑
τ−τα++
∂
τ∂
−
∂
τ∂
λ=
τ∂
τ∂
ρ
i
iFiid
xtxtSq
x
xt
cG
x
xt
S
xt
cS .П,,
,,,
2
2
(14.8)
Далее, поделив уравнение почленно на произведение
cS
ρ
и перегруппировав слагаемые, получим
окончательный вид уравнения:
(
)
(
)
(
)
() ()
,,,
,,,
2
2
τ=τ+
∂
τ∂
+
∂
τ∂
−
τ∂
τ∂
xPxKt
x
xt
W
x
xt
a
xt
(14.9)
где −
ρ
λ
=
c
a температуропроводность жидкости;
−
ρ
=
S
G
W
скорость движения жидкости;
()
()
....,,1;
,П
,;
П
Ni
cS
xtSq
xP
cS
K
i
Fiiid
i
ii
=
ρ
τα+
=τ
ρ
α
=
∑
∑
(14.10)
Используя условия однозначности
() ()() ()
()
0
,0
;0,;,0
0
=
∂
τ∂
=τ=τ
x
t
xfxttt
, (14.11)

находим решение задачи (14.9) – (14.11).
Решение ищем в виде
(
)
(
)( )
,,exp, τ
τ
ϕ
+
φ
=
τ
xuxxt (14.12)
где
.
2
;
4
2
a
W
a
W
K =ϕ−−=φ
(14.13)
Тогда
(
)
(
)
(
)
()
,0,0,
exp
,,,
2
2
τ≤≤≤
τϕ+φ
τ
+
∂
τ∂
=
τ∂
τ∂
rx
x
xP
x
xu
a
xu
(14.14)
()
(
)
()
()
(
)
()
()
()
.0,
,
,
exp
,0,
exp
0,
0
=τφ+
∂
τ∂
τϕ
τ
=τ
φ
= ru
x
ru
t
u
x
xf
xu
(14.15)
Вводим конечное интегральное преобразование вида
() ( ) ()
∫
τ=τ
r
dxxSxuT
0
,
, (14.16)
где
()
−xS ядро интегрального преобразования, являющееся решением вспомогательной задачи
(
)
()
xS
dx
xSd
2
2
2
µ−= ; (14.17)
()
(
)
()
;0;00 =φ+= rS
dx
rdS
S
(14.18)
(
)
(
)
,sin xxS
nn
µ
=
(14.19)
где
−
µ
n
последовательные положительные корни уравнения
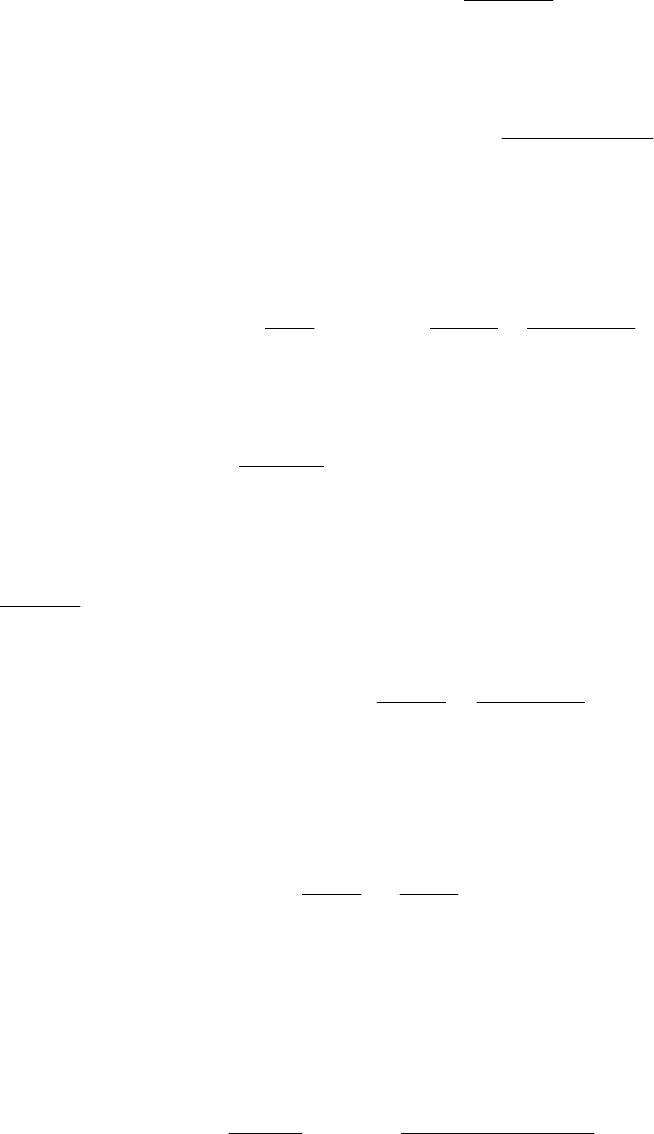
(
)
(
)
.0sincos =
µ
φ
+
µ
µ
rr (14.20)
Весовая функция в преобразовании (14.16) для уравнения (14.14) равна 1.
Обратный переход выполняется по формуле
()
(
)()
,,
1
∑
∞
=
τ
=τ
n
n
nn
Z
xST
xu
(14.21)
где
()
()()
.
cossin
5,0
0
2
µ
µµ
−==
∫
n
nn
r
nn
rr
rdxxSZ
(14.22)
Переход к изображениям позволяет найти функцию
(
)
τ
T как решение задачи:
()
()
(
)
()
()()
()
,
exp
,
exp
0
0
2
∫
φ+τϕ
τ
+
τϕ
τµ
+τµ−=
τ
τ
r
dx
x
xSxP
ta
Ta
d
dT
(14.23)
()
(
)
(
)
()
∫
φ
=
r
dx
x
xSxf
T
0
exp
0
.
()
()
() ()
()
+
φ
τµ−=τ
∫
r
dx
x
xSxf
aT
0
2
exp
exp
()
()
()
()()
()
.
exp
,
exp
exp
0
0
0
2
τ
φ+τϕ
τ
+
τϕ
τµ
τµ+
∫∫
τ
ddx
x
xSxP
ta
a
r
(14.24)
Если молекулярным переносом тепла можно пренебречь, нестационарное уравнение переноса тепла
жидкостью, движущейся в режиме идеального вытеснения по каналу, образованному N поверхностями,
упрощается:
(
)
(
)
() ()
,,,
,,
τ=τ+
∂
τ∂
+
τ∂
τ∂
xFxKt
x
xt
W
xt
(14.25)
где W – скорость движения жидкости;
()
()
....,,1;
,П
,;
П
Ni
cS
xtSq
xF
cS
K
i
Fiiid
i
ii
=
ρ
τα+
=τ
ρ
α
=
∑
∑
(14.26)
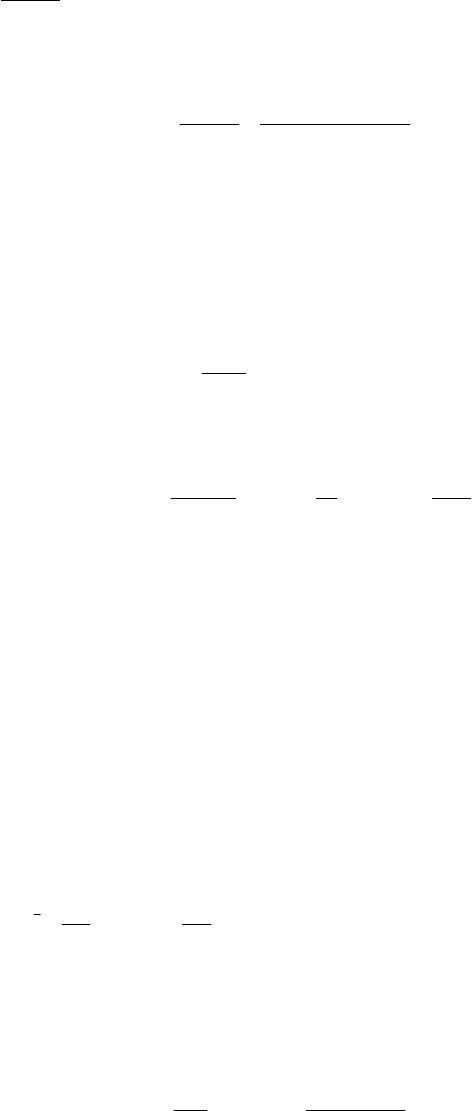
Условия однозначности
(
)
(
)
(
)()
xfxttt =
τ
=
τ
0,;,0
0
. (14.27)
При моделировании температурных полей потоков как совокупностей температурных полей эле-
ментарных областей возможно использование приближенного решения задачи (14.25) – (14.27), полу-
ченного при замене частной производной
(
)
τ∂
τ∂ ,xt
конечно-разностным аналогом:
(
)
(
)
(
)
.
,,,
τ
τ−τ−τ
≈
τ∂
τ∂
d
dxtxtxt
(14.28)
При этом для фиксированного значения времени dτ внутри каждого временного интервала темпера-
турное поле потока является функцией только координаты х и описывается уравнением:
(
)
() ()
xVxPt
dx
xdt
=+
, (14.29)
где
() ()
()
,,
1
;
1
τ
+τ=
τ
+τ
=
d
xf
dxF
W
xV
dW
dK
P
(14.30)
t
0
(х) – температурное поле теплоносителя в элементарной области в начальный момент.
При начальном условии вида
()
0
0 tt = имеем решение уравнения (14.29):
() ( ) () ( )
.expexp
0
0
+−=
∫
x
dxPxxVtPxxt (14.31)
Средняя температура жидкости на участке длиной ∆х равна
() () ()()
.expexp
11
0
0
00
dxdPVtPx
x
dxxt
x
t
x
xx
ξξξ+−
∆
=
∆
=
∫∫∫
∆∆
(14.32)
Если канал образован одной стенкой замкнутого периметра с температурой
()
,,τxt
F
то
()
()
,
,П
,;
П
cS
xt
xF
cS
K
F
ρ
τα
=τ
ρ
α
=
(14.33)

где П – периметр сечения канала; α – коэффициент теплоотдачи.
В стационарном случае задача упрощается:
(
)
() ()
xSxKt
dx
xdt
=+
, (14.34)
где
()
()
(
)
.
ПП
;
ПП
2221112211
Gc
xtxt
xS
Gc
K
FF
α+α
=
α+α
=
(14.35)
При начальном условии вида
()
0
0 tt = решение уравнения (14.34) имеет вид:
() ( ) () ( )
.expexp
0
0
+−=
∫
x
dxKxxStKxxt (14.36)
Если температуры стенок постоянны, т.е.
(
)
11
const
FF
txt
=
=
и
(
)
22
const
FF
txt =
=
, то
(
)
(
)
(
)
,exp
0
KxVtVxt
−
−
+
=
(14.37)
где
(
)()
.
ПП
ПП
2211
222111
α+α
α+α
=
xtxt
V
FF
(14.38)
Средняя температура жидкости на участке длиной ∆х равна
()
()
()()
.exp1
1
0
0
Kx
xK
Vt
Vdxxt
x
t
x
−−
∆
−
+=
∆
=
∫
∆
(14.39)
Если канал образован одной стенкой замкнутого периметра с температурой
()
xt
F
, то
() ( ) () ( )
,expexp
0
1101
+−=
∫
x
F
dxxKxtKtxKxt
(14.40)
где
.
П
1
Gc
K
α
=
Если температура стенки постоянна, т.е.
(
)
FF
txt
=
=
const , то
(
)
(
)( )
xKtttxt
FF 10
exp −
−
+
=
, (14.41)
а средняя температура жидкости на участке длиной ∆х равна
()
()
()()
.exp1
1
1
1
0
0
xK
xK
tt
tdxxt
x
t
F
F
x
−−
∆
−
+=
∆
=
∫
∆
(14.42)
15 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ
СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
Решение ряда прикладных инженерных задач в области процессов и аппаратов химических техно-
логий может быть основано на математическом моделировании температурных полей в рабочих объе-
мах и конструкционных элементах промышленного оборудования.
Использование аналитических решений нелинейных задач теплопроводности существенно расши-
ряет возможности данного подхода и повышает качественные характеристики результатов математиче-
ского моделирования.
При математическом моделировании температурного поля
элементарной области температурное поле в начале элементарного интервала
времени известно, поэтому тепло- проводность среды, в которой
протекает тепловой процесс, формально может быть представлена,
как функция пространственных ко- ординат, а не температуры. Это дает
возможность получить аналитические решения ряда нелинейных задач
теплопроводности.
Рассмотрим решение нелинейных задач стационарной теплопроводности
для тел канонической формы в декартовых и цилиндрических коор-
динатах.
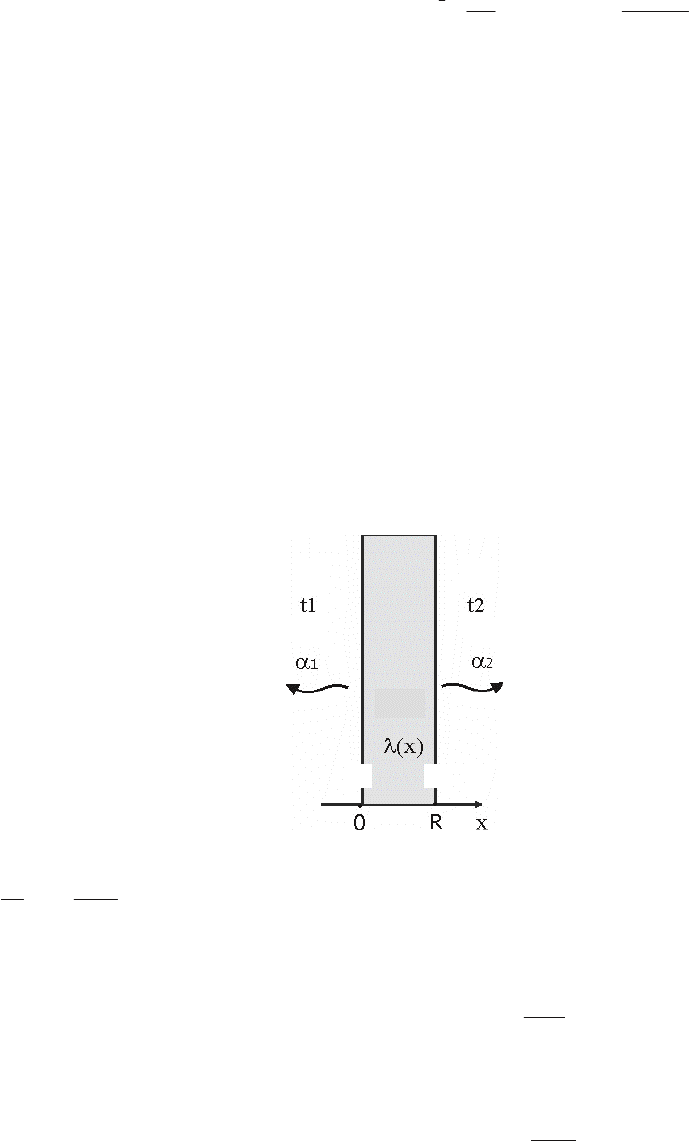
Температурное поле неограниченной пластины (рис. 15.1)
моделируется решением следующей задачи теплопроводности:
()
()
;0,0 Rx
dx
xdt
x
dx
d
≤≤=
λ
(15.1)
()
(
)
()()
;00
0
0
11
=−α−λ tt
dx
dt
(15.2)
()
(
)
()()
.0
22
=−α+λ tRt
dx
Rdt
R
(15.3)
R
х
0
t
2
t
1
α
1
α
2
λ
(
х
)

Здесь t(x) – температурное поле пластины; x – пространственная координата; R – толщина пласти-
ны; λ(x) – коэффициент теплопроводности пластины как функция координаты; α
1
, α
2
– коэффициенты
конвективной теплоотдачи; t
1
, t
2
– температуры окружающей среды.
Решение задачи (15.1) – (15.3) осуществляется путем интегрирования (15.1):
()
(
)
.A
dx
xdt
x =λ
(15.4)
Это уравнение, в свою очередь, так же может быть проинтегрировано:
()
()
.
00
∫∫
λ
=
′
xx
x
dx
Adxxt
(15.5)
Отсюда получаем общее решение уравнения (15.1):
() ()
()
.0
0
∫
λ
+=
x
x
dx
Atxt
(15.6)
Используя граничные условия (15.2) – (15.3), находим значения t (0) и А.
В результате
()
()
()
,
1
11
0
1
0
21
12
1
λ
+
α
α
+
λ
+
α
−
+=
∫
∫
x
R
x
dx
x
dx
tt
txt
(15.7)
где t(x) – искомое распределение температуры по толщине пластины.
Аналогично моделируется поле температур в полом неограниченном цилиндре (рис. 15.2):
()
()
;,0
21
RrR
dr
rdt
rr
dr
d
≤≤=
λ
(15.8)
()
()
()()
;0
111
1
1
=−α−λ tRt
dr
Rdt
R
(15.9)
()
()
()()
.0
222
2
2
=−α+λ tRt
dr
Rdt
R
(15.10)
t
1
t
2
α
1
α
2

Здесь t(r) – температурное поле цилиндра; r – пространственная координата; R
1
, R
2
– соответствен-
но внутренний и наружный радиусы цилиндра; λ(r) – коэффициент теплопроводности цилиндра как
функция координаты; α
1
, α
2
– коэффициенты конвективной теплоотдачи; t
1
, t
2
– температуры окружаю-
щей среды.
Решение задачи (15.8) – (15.10) осуществляется путем интегрирования (15.8):
()
(
)
.A
dr
rdt
rr =λ
(15.11)
Это уравнение, в свою очередь, также может быть проинтегрировано:
()
()
.
11
∫∫
λ
=
′
r
R
r
R
rr
dr
Adrrt
(15.12)
Отсюда получаем общее решение уравнения (15.8):
() ( )
()
.
1
1
∫
λ
+=
r
R
rr
dr
ARtrt
(15.13)
Используя граничные условия (15.9) – (15.10), находим значения
(
)
1
Rt и А.
В результате
()
()
()
.
1
11
1
1
1
11
2211
12
1
λ
+
α
α
+
λ
+
α
−
+=
∫
∫
r
R
R
R
rr
dr
R
Rrr
dr
R
tt
trt
(15.14)
Полученные аналитические решения нелинейных задач стационарной теплопроводности не только
имеют самостоятельную прикладную ценность, но и входят в качестве составных частей в аналитиче-
ские решения соответствующих нелинейных задач нестационарной теплопроводности.
15.1 Решение нелинейной нестационарной задачи теплопроводности
Теоретическая возможность использования метода конечных интегральных преобразований для
решения нелинейных задач не исключается, но даже в специальной математической литературе можно
встретить отказы от рассмотрения таких решений ввиду их чрезмерной сложности.
Однако, для ряда прикладных инженерных задач, связанных с расчетом технологического оборудова-
ния химической промышленности, могут быть получены аналитические решения нелинейных задач теп-
лопроводности.
0
r
R
2
R
1
λ
(
r
)
