Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.


81
и
()
(
)
µ
ρ+⋅λλ
−=
µ
⋅λλ
−=Φ⋅λλ=ηξϕ
ghpP
,
2121
21
. (3)
Система уравнений (3.4) в рассматриваемом случае I
3
= λ
1
λ
2
= const совпадает с
системой (1). Поэтому систему (1) можно привести к каноническому виду с помо-
щью перехода к новым независимым переменным ξ
1
, η
1
, которые выбираются из
частных решений самой же системы (1). Каноническая форма (3.6′) системы (1)
ввиду постоянства инварианта I
3
и равенства (3) принимает вид условий Коши-
Римана
1111
;
ξ∂
ψ∂
−=
η∂
ϕ∂
η∂
ψ∂
=
ξ∂
ϕ∂
. Поэтому все решения ϕ(ξ, η) и ψ(ξ, η) системы (1)
выражаются через аналитические функции
ϕ(ξ, η) + i⋅ψ(ξ, η) = w(ζ) (4)
комплексного переменного ζ = ξ
1
+ i⋅η
1
, где ξ
1
и η
1
- некоторые частные решения
самой же системы (1). Такой вывод о решениях системы (1), являющейся в ввиду
тождества a⋅c – b
2
≡ 1 системой Бельтрами, совпадает с общей теорией этих систем
[20]. Далее аналитическую функцию w(ζ) называем комплексным потенциалом
плоскопараллельного течения в однородной анизотропной среде.
В заключение отметим, что если комплексный потенциал течения w(ζ) найден
и, тем самым, функции ϕ(ξ, η) и ψ(ξ, η) определены, то тогда поле скоростей
фильтрации вычислим через ϕ(ξ, η) по формулам (3.3), которые с учётом равенств
(2) и (3) перепишутся в виде
η∂
ϕ
∂
+
ξ∂
ϕ
∂
=
η∂
ϕ
∂
+
ξ∂
ϕ∂
=
ηξ
G
c
E
b
v;
G
b
E
a
v
, (5)
а через ψ(ξ, η) - по формулам (1.14).

82
2.5. Комплексные потенциалы плоскопараллельных фильтрационных тече-
ний в анизотропно-однородных средах со специальными законами распреде-
ления ГНА
2.5.1. Теорема о комплексном потенциале для специальной серии законов распре-
деления ГНА. Выберем в плоскости плоскопараллельного фильтрационного тече-
ния в однородной анизотропной среде изотермические криволинейные координа-
ты ξ и η. Такие координаты задаются при помощи некоторой аналитической
функции ω(z) комплексного переменного z = x + i⋅y (где x и y – декартовые коор-
динаты) формулой [41, 44]
(
)
(
)
(
)
zy,xiy,x
ω
=
η
⋅
+
ξ
. (1)
Одно из ГНА пористых сред, в которых изучаются течения жидкости, по-
прежнему расположено перпендикулярно к плоскости течения, а законы рас-
пределения двух других ГНА определим при помощи семейств попарно-
ортогональных кривых p(ξ, η) = const и q(ξ, η) = const. Эти функции p(ξ, η) и
q(ξ, η), определяющие всевозможные законы распределения ГНА, будем зада-
вать при помощи равенств
,d)(H),(p
0
∫
η
η
ηηβ−αξ=ηξ
∫
η
η
η
η
α+βξ=ηξ
0
)(H
d
),(q
, (2)
где α и β - произвольные одновременно не равные нулю постоянные, а H(η)- про-
извольная положительная непрерывная функция, геометрический смысл которой в
том, что она определяет угол γ пересечения линий q(ξ, η) = const с координатными
линиями η = const:
)(Htg η
α
β
−=γ . (3)
Для данного класса анизотропных сред компоненты тензора проницаемости в изо-
термических координатах
);(
η
ξ примут, согласно формуле (1.3.6), значения
()
постоянныеи;constkkk)(k
)(H
)(H
k
),(k
)(H
))((H
kk),(k
)(H
)(H
k
2121
2
12221122
222
2
2
1
22
22
12
222
12
211211
222
2
22
1
2
11
−λλ=λλ=−η=
ηβ+α
λα+ληβ
=
η=
ηβ+α
λ−ληαβ
==η=
ηβ+α
ληβ+λα
=
. (4)
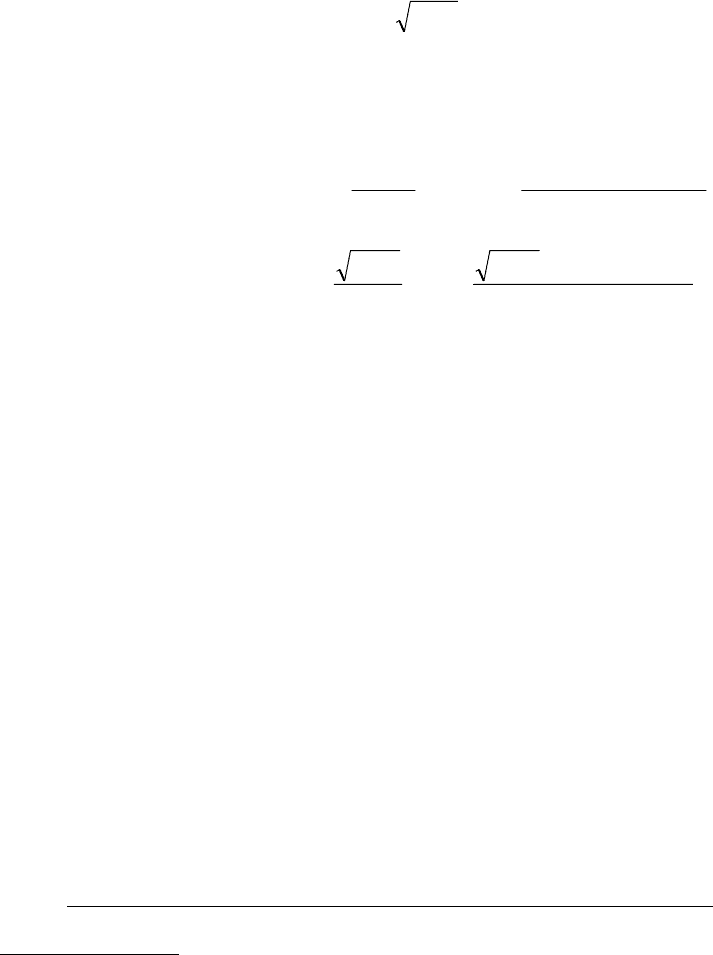
83
Комплексные потенциалы плоскопараллельных фильтрационных течений в анизо-
тропно-однородных средах представляют собой, как доказано в §2.4, аналитиче-
ские функции комплексного переменного ζ = ξ
1
+ i⋅η
1
, действительная ξ
1
и мнимая
η
1
части которого удовлетворяют системе уравнений (4.1). Решения системы урав-
нений (4.1) благодаря тому, что компоненты тензора проницаемости (4) зависят
только от одной переменной η и
const
21
=λλ , удаётся построить с помощью опе-
рации Σ - интегрирования Берса и Гельбарта [234, 235]. В частности, как легко
проверить, решениями ξ
1
и η
1
системы (4.1) будут функции
(
)
()
∫
η
λα+ληβ
λ−ληαβ
−ξ
∫
=η
η
η
−ξ=ξ
η
η
η
η
00
;d
)(H
))((H
d
k
k
2
2
1
22
12
22
12
1
(5)
()
∫∫
η
λα+ληβ
ηβ+αλλ
=η
η
λλ
=η
η
η
η
η
00
.d
)(H
))(H(
d
k
2
2
1
22
222
21
22
21
1
(6)
Полученный результат сформулируем в виде следующей
теоремы: аргумент
ζ
=
ξ
1
+ i
⋅η
1
комплексных потенциалов
(
)
(
)()
ζ
=
η
ξ
ψ
⋅
+
η
ξ
ϕ
w,i, плоскопараллель-
ных фильтрационных течений в однородных анизотропных средах, законы
распределения ГНА в которых задаются формулами (2), определяется по фор-
мулам(5) и (6).
Формулы (5) и (6) исчерпывают весь запас известных случаев
(В.И. Аравин [2-6], Е.С. Ромм [120, 121], Г.К. Михайлов [90], Н.Р. Рабинович
[113] и др.), когда плоскопараллельные течения в анизотропно-однородных
средах исследуются методами аналитических функций комплексного перемен-
ного с помощью «изотропизирующих» подстановок.
Отметим ряд следствий, вытекающих из сформулированной теоремы.
2.5.2.
Следствие 1. Конгруэнтные законы распределения ГНА
Определение 1. Средами с конгруэнтными законами распределения ГНА будем на-
зывать грунты, в которых все кривые одного из двух семейств линий, определяю-
щих ГНА, пересекают любую прямую
l
из некоторого семейства L параллельных
прямых под одним и тем же углом
)(l
γ
.
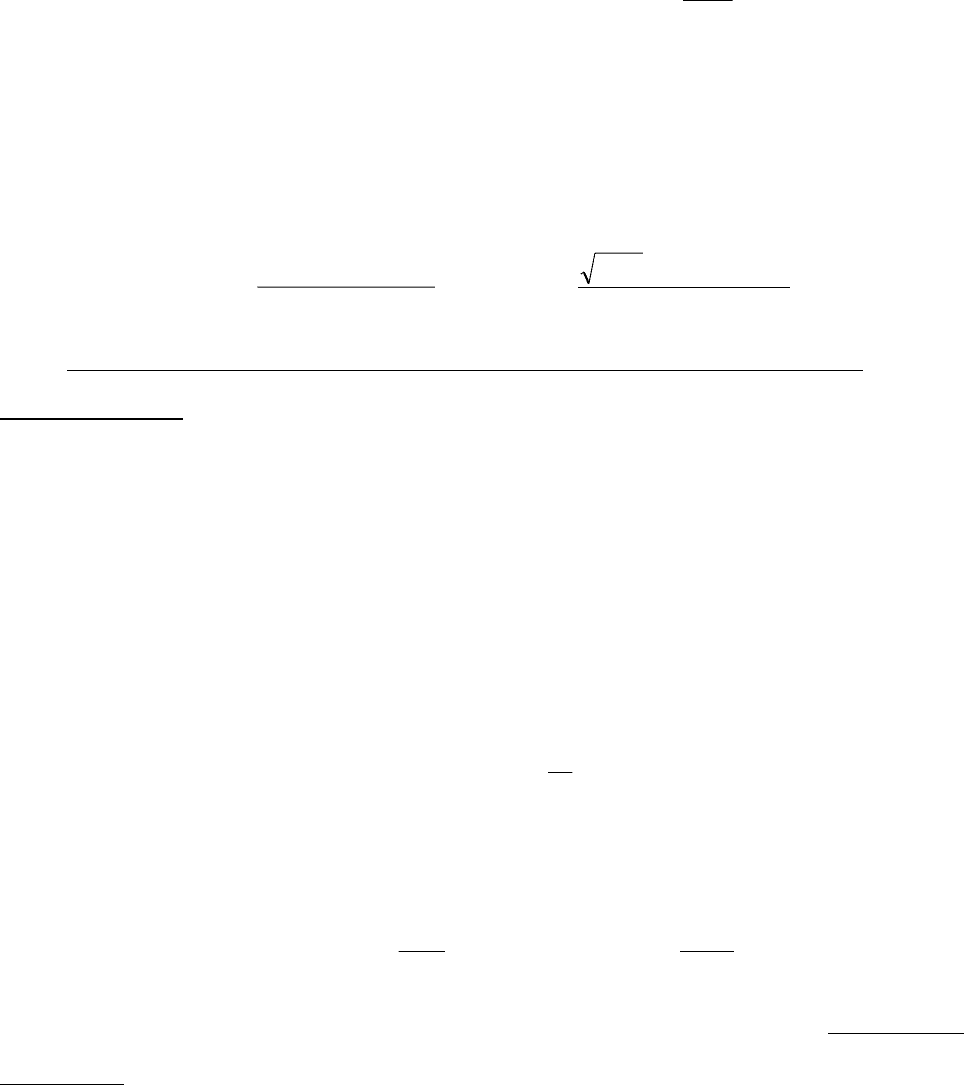
8
4
Плоскопараллельную фильтрацию в этих средах будем изучать в декартовой
системе координат x, y, ось x которой совмещена с одной из прямых
l из семейства
L. Поэтому функцию ω(z) в (1) задаём в виде ω(z) = z и, следовательно, ξ = x и η =
y. Уравнения p(x, y)= const и q(x, y)= const ортогональных ГНА сред с конгруэнт-
ной анизотропией в декартовой системе координат в соответствии с (2) определя-
ются при помощи формул
() () ()
()
∫∫
Η
α+β=Ηβ−α=
y
dy
xy,xq;dyyxy,xp
. (7)
Эти формулы обобщают закон распределения ГНА, именуемый прямолинейной
анизотропией, который получается из (7) при H(y) = 1. Формулы (5) и (6), опреде-
ляющие аргумент ζ= ξ
1
+ i⋅η
1
комплексного потенциала для сред с конгруэнтными
законами распределения ГНА, дадут выражения
()
(
)
()
()
[
]
()
∫∫
λΗβ+λα
Ηβ+αλλ
=η
λΗβ+λα
λ−λΗαβ
+=ξ
y
0
1
22
2
2
222
21
1
y
0
1
22
2
2
21
1
dy
y
y
;dy
y
y
x . (8)
2.5.3.
Следствие 2. Центрально-симметричные законы распределения ГНА
Определение 2.
Средами с центрально-симметричными законами распределения
ГНА будем называть грунты, в которых все кривые одного из двух семейств линий
ГНА, сходясь в некоторой точке C, пересекают любую окружность с радиусом r
и с центром в C под одним и тем же углом
(
)
r
γ
.
Плоскопараллельную фильтрацию в этих средах удобно изучать в полярной
системе координат r, θ полюс которой совмещен с точкой C. Именно поэтому
функцию (1) сейчас зададим в виде ω(z)=i⋅
ln z и, следовательно, ξ = −θ, а η = ln r.
Учитывая, что в рассматриваемом случае
θ−=ξ=η ddа,
r
dr
d , уравнения (4) ортого-
нальных криволинейных линий
(
)
(
)
const,rqиconst,rp
=
θ
=
θ
ГНА в полярных коор-
динатах примут вид
()
(
)
()
()
∫∫
αθ+
Η
β=θβθ−
Η
α=θ
rr
dr
,rq;dr
r
r
,rp . (9)
(Постоянные в (2) для удобства были сейчас переобозначены по схеме: α, β в (2) →
β, −α в (9)
, что, конечно, не существенно). Формулы (5) и (6) (с учётом принятой

85
схемы переобозначений постоянных α, β) для аргумента ζ= ξ
1
+ i⋅η
1
комплексного
потенциала течений в средах с центрально-симметричными законами распределе-
ния ГНА дадут выражения
()( )
()
[]
()
[
]
()
[]
∫∫
λ⋅β+λ⋅α⋅
⋅β+α⋅λλ
=ηθ−
λ⋅β+λ⋅α⋅
⋅λ−λ⋅⋅αβ
=ξ
r
r
2
2
1
22
222
21
1
r
r
2
2
1
22
12
1
00
rHr
drrH
;
rHr
drrH
. (10)
Однако комплексные потенциалы w(ζ) плоскопараллельных течений в рассматри-
ваемых средах удобнее строить не с помощью аргумента ζ, а с помощью вспомо-
гательного комплексного переменного Z(ζ), которое определим равенством
ζ⋅−
⋅=
i
0
erZ . С учётом формул (10) для аргумента ζ = ξ
1
+ i⋅η
1
вспомогательное пе-
ременное
ζ⋅−
⋅=
i
0
erZ будет определяться по формуле
(
)
(
)
θω⋅
⋅=
,ri
erRZ , (11)
где
()
()
[
]
()
[]
()
()( )
()
[]
∫∫
λ⋅β+λ⋅Ηα⋅
⋅λ−λ⋅Ηαβ
−θ=θω
λ⋅β+λ⋅Ηα⋅
⋅β+Ηαλλ
⋅=⋅=
η
r
r
2
2
1
22
12
r
r
2
2
1
22
222
21
00
00
1
rr
drr
,r;
rr
drr
exprerrR
.(12)
Удобство применения в решении конкретных задач комплексного переменного Z
объясняется тем, что на окружности x
2
+ y
2
= r
0
2
переменное Z совпадает с обыч-
ным комплексным переменным x + i⋅y, т.е.
θ⋅
=
⋅=
i
0
rr
erZ
0
, что непосредственно сле-
дует из (11) и (12). Итак, комплексные потенциалы плоскопараллельных течений в
средах с центрально-симметричными законами распределения ГНА (9) будут оп-
ределяться по формуле ϕ(r, θ) + i⋅ψ(r, θ) = w(Z), где w(Z) – произвольная аналити-
ческая функция комплексного переменного Z, определяемого формулами (11) и
(12).
2.5.4. Следствие 3. Изотермические законы распределения ГНА
Определение 3.
Средами с изотермическими законами распределения ГНА будем
называть грунты, в которых ГНА в каждой точке (x, y) направлены по касатель-
ным к линиям уровня двух сопряжённых [78] гармонических функций p(x, y) и q(x,
y).
В соответствии с определением 3 задание конкретного изотермического зако-
на распределения ГНА определяется выбором некоторой аналитической функции

86
p(x, y) + i⋅q(x, y) = ω(z) (13)
комплексного переменного z = x + i⋅y. Плоскопараллельную фильтрацию в средах
с изотермическими законами распределения ГНА удобно изучать в криволинейной
системе координат (ξ, η), совмещённой с ГНА (13). Совмещение системы коорди-
нат (ξ, η) с ГНА (13) достигается выбором в формулах (2) функции
1)(H
=
η
и по-
стоянных α = 1, β = 0 и η
0
=0. Тогда )y,x(p
=
ξ
и )y,x(q
=
η
. Для построения ком-
плексных потенциалов плоскопараллельных фильтрационных течений в рассмат-
риваемых средах остаётся определить аргумент ζ= ξ
1
+ i⋅η
1
. В соответствии с фор-
мулами (5) и (6) в рассматриваемом случае получаем, что ξ
1
= ξ = p(x, y) и
()
y,xq
2
1
2
1
1
⋅
λ
λ
=η⋅
λ
λ
=η
. Таким образом, комплексные потенциалы плоскопарал-
лельных течений в средах с изотермическими законами распределения ГНА (13)
будут определяться по формуле
ϕ(x, y) + i⋅ψ(x, y) = w(ζ) , где
() ()
y,xqiy,xp
2
1
⋅
λ
λ
⋅+=ζ
. (14)
Ранее конкретные задачи линейной плоскопараллельной фильтрации, главным об-
разом, в средах с прямолинейной (
z)z(
=
ω
) и радиальной ( zln)z( =ω ) анизотропией
рассматривались в работах В.И. Аравина [2-6], В.А. Брагинской [21],
О.В. Голубевой [39, 40, 44, 45], А.Т. Горбунова [47], В.С. Козлова [67],
Г.К. Михайлова [88-90], П.Я. Полубариновой-Кочиной [106], Ю.Л. Соломко [130],
С.Е. Холодовского [216, 218-223], Х. Маркуса и Д.Е. Ивентона [245],
И. Литвинишина [242] и др. Доказанная в п. 2.5.1. теорема и её следствия 1, 2, 3
указывают способ описания плоскопараллельных фильтрационных течений в ани-
зотропных средах с самыми разнообразными законами распределения ГНА. Все
рассматриваемые ранее другими авторами законы распределения ГНА и соответ-
ствующие им виды комплексных потенциалов из этой теоремы и её следствий вы-
текают как частные случаи.

87
2.5.5 Типичные граничные условия для комплексных потенциалов плоскопа-
раллельных течений в анизотропных средах. Перечислим наиболее часто
встречающиеся на практике ситуации и выпишем соответствующие им гранич-
ные условия для комплексных потенциалов фильтрационных течений.
В §2.1 уже было отмечено одно из граничных условий: на контуре
l непро-
ницаемого тела функция тока сохраняет постоянное значение
const=ψ
l
. (15)
На практике часто встречаются ситуации, когда в области фильтрации быва-
ют известны линии С, вдоль которых известно распределение приведённого дав-
ления Р. Как правило, эти линии являются границами областей питания или же
границами эксплутационных и нагнетательных скважин. Так как давление Р связа-
но с
ϕ
зависимостью (4.3), то вдоль упомянутых линий С известно распределение
значений ϕ. Поэтому ещё одно граничное условие имеет вид :
)M(f
C
=ϕ , где
−
∈
f,CM заданная функция. (16)
Другой часто встречающейся на практике ситуацией является та, когда
фильтрация происходит в двух (или более) кусочно-однородных средах (рис.8). В
этом случае фильтрация описывается двумя комплексными потенциалами w
1
(ζ) и
w
2
(ζ) в 1-ой и 2-ой средах соответственно, а на границе S их раздела требуют не-
прерывность давления и нормальной составляющей вектора скорости фильтрации,
т. е.
21
PP = и
n2n1
vv
=
. С помощью функций ϕ и ψ условие сопряжения комплекс-
ных потенциалов w
1
(ζ) и w
2
(ζ) на границе S раздела двух кусочно-однородных
анизотропных сред записывается следующим образом [45, 143, 154, 173]:
S
2
S
1
S
2221
2
S
1211
1
; ψ=ψ
λλ
ϕ
=
λλ
ϕ
. (17)
2.6. Комплексные потенциалы плоскопараллельных течений в однородных
средах с прямолинейной анизотропией при произвольной ориентации ГНА
В предыдущих параграфах §2.3 и §2.4 рассматривались уравнения для плос-
копараллельных фильтрационных течений в анизотропных пластах с плоскими и
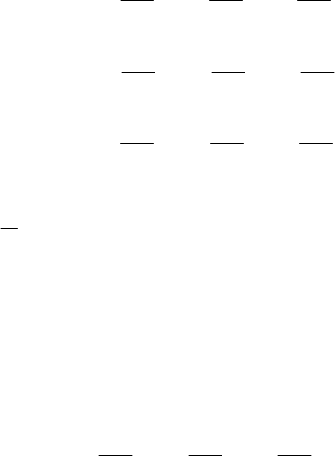
88
параллельными друг другу подошвой и кровлей, когда одно из ГНА пласта было
всюду перпендикулярно подошве и кровле. В этом параграфе доказывается, что
плоскопараллельная фильтрация в однородных пористых средах с прямолинейной
анизотропией вне зависимости от ориентации ГНА относительно подошвы и кров-
ли слоя тоже описывается комплексными потенциалами, представляющими собой
аналитические функции.
Если ГНА {
'
3
'
2
'
1
e,e,e
r
r
r
} и соответствующие им постоянные главные проницае-
мости λ
1
, λ
2
, λ
3
среды с прямолинейной анизотропией будут заданы, то компонен-
ты тензора проницаемости в расчетной декартовой системе координат (x, y, z) с
ортами
ke,je,ie
321
r
r
r
r
r
r
=== найдутся по формуле (1.3.6). Пусть для конкретности в
подошве (кровле) плоскопараллельного слоя, заполненного средой с прямолиней-
ной анизотропией, меняются координаты х и у, а ось z направлена по толщине
слоя. Распределение скорости фильтрации в такой среде в декартовых координатах
согласно тензорному закону Дарси (1.3.9) найдем из уравнений
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
=
z
Ф
k
y
Ф
k
x
Ф
kv
z
Ф
k
y
Ф
k
x
Ф
kv
z
Ф
k
y
Ф
k
x
Ф
kv
333231z
232221y
131211x
, (1)
где все k
ij
=k
ji
=const, а
µ
−=Φ
Р
. Выясним, когда течение (1) будет плоскопараллель-
ным относительно подошвы и кровли слоя. Для этого, очевидно, проекция скоро-
сти фильтрации v
z
должна быть равна нулю, т.е. согласно (1) должно выполняться
условие
0
z
Ф
k
y
Ф
k
x
Ф
kv
333231z
=
∂
∂
+
∂
∂
+
∂
∂
= . (2)
Будем рассматривать (2) как уравнение первого порядка относительно Ф. Ре-
шая (2) известными методами [59], найдем, что
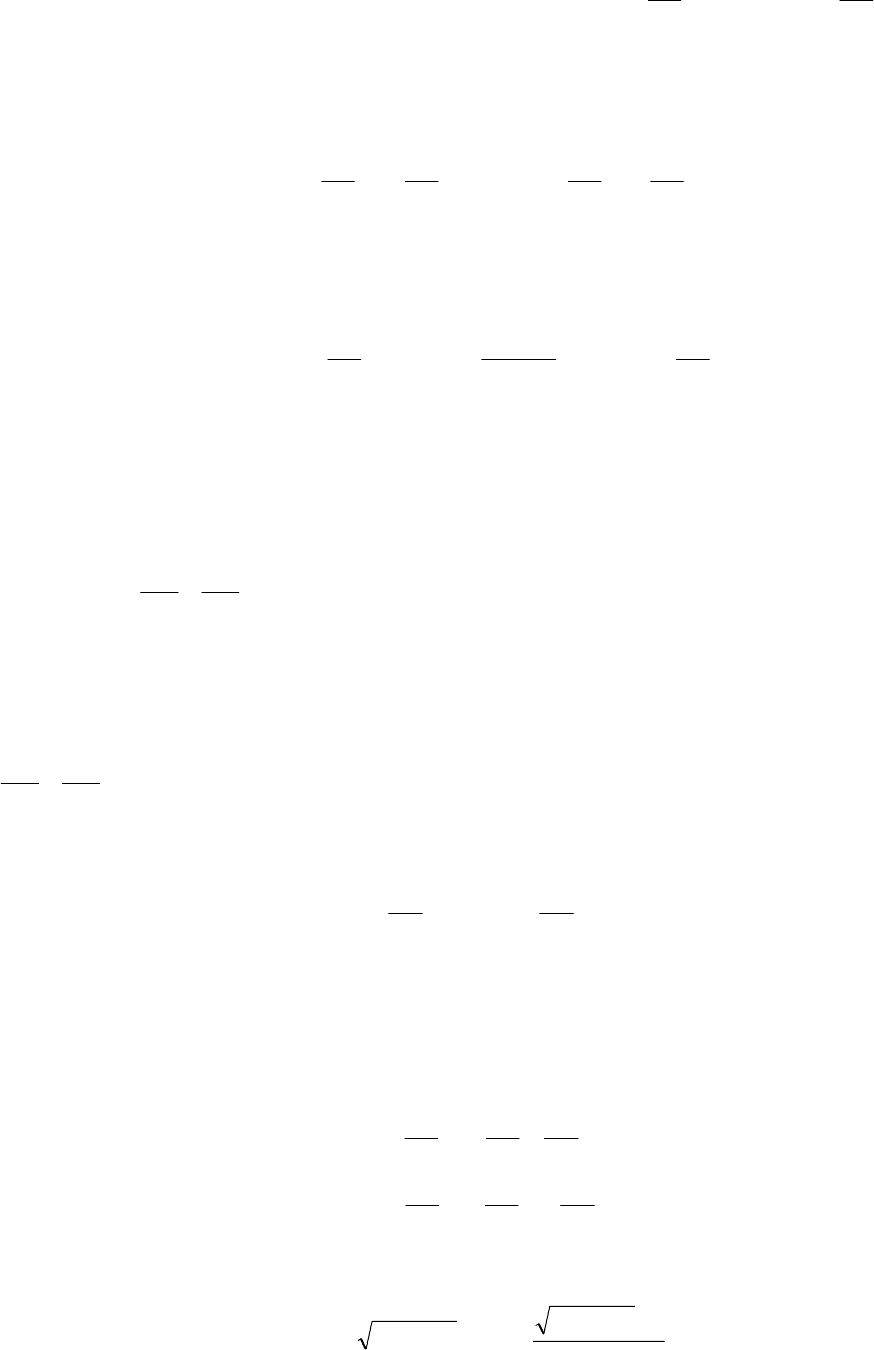
89
)Y,Х(ФФ = - произвольная функция от z
k
k
yY;z
k
k
xX
33
23
33
13
⋅−=⋅−= . (3)
Подставляя теперь (3) в первые два уравнения системы (1), для проекций ско-
рости фильтрации v
x
и v
y
найдем следующие выражения:
Y
Ф
c
X
Ф
bv;
Y
Ф
b
X
Ф
av
yx
∂
∂
⋅+
∂
∂
⋅=
∂
∂
⋅+
∂
∂
⋅= . (4)
В (4) через a, b и с – обозначены постоянные с размерностью проницаемости,
имеющие вид
33
2
23
22
33
2313
12
33
2
13
11
k
k
kc;
k
kk
kb;
k
k
ka −=
⋅
−=−=
. (5)
Кроме обобщённого на рассматриваемый случай закона Дарси поле скорости
фильтрации должно удовлетворять уравнению неразрывности несжимаемой жид-
кости. С учетом того, что v
z
=0, уравнение неразрывности будет, как известно,
иметь вид:
0
y
v
x
v
y
x
=
∂
∂
+
∂
∂
. Формулы (3) и (4) показывают, что v
x
и v
y
– сложные
функции, с промежуточными аргументами X и Y, т.е.
)Y,X(vv
xx
=
и )Y,X(vv
yy
=
.
Подставляя v
x
и v
y
в уравнение неразрывности, получим для него новое выражение
0
Y
v
X
v
y
x
=
∂
∂
+
∂
∂
, из которого следует существование функции Ψ=Ψ(X, Y), позволяю-
щей выразить стандартным для гидродинамики способом скорости v
x
и v
y
через Ψ:
X
v;
Y
v
yx
∂
Ψ
∂
−=
∂
Ψ
∂
= . (6)
Сравнивая теперь формулы (4) и (6), получаем следующую систему уравне-
ний, описывающую плоскопараллельную фильтрацию в плоскости xoy в однород-
ной среде с прямолинейной анизотропией при произвольной ориентации ГНА:
∂
Ψ∂
−=
∂
∂
⋅+
∂
∂
⋅
∂
Ψ∂
=
∂
∂
⋅+
∂
∂
⋅
ХY
Ф
c
X
Ф
b
YY
Ф
b
X
Ф
a
. (7)
Если вместо Ф ввести в рассмотрение функцию
µ
⋅−⋅
−=⋅−⋅=ϕ
Рbca
Фbca
2
2
, (8)
то система уравнений (7) примет вид

90
∂
Ψ∂
−=
∂
ϕ∂
⋅+
∂
ϕ∂
⋅
∂
Ψ∂
=
∂
ϕ∂
⋅+
∂
ϕ∂
⋅
ХY
c
X
b
YY
b
X
a
00
00
, (9)
где
2
0
2
0
2
0
bac
c
c,
bac
b
b,
bac
a
a
−
=
−
=
−
=
. (10)
Но поскольку
1bca
2
000
=−⋅ , то система уравнений (9) будет системой уравне-
ний Бельтрами. На основании свойств [20, 28] системы Бельтрами вытекает, что
всевозможные её решения можно построить с помощью аналитической функции
w(ζ) комплексного переменного ζ=ϕ
0
+iψ
0
по формуле
)(w)Y,X(i)Y,X(
ζ
=
Ψ
+
ϕ
, (11)
в которой ϕ
0
и ψ
0
любое конкретное частное решение исходной системы (9). Такое
решение при постоянных а
0
, b
0
и c
0
легко найти. Например, частное решение сис-
темы (9) дают функции
Y
c
1
;Y
c
b
X
0
0
0
0
0
⋅=Ψ⋅−=ϕ . (12)
Выполненные расчёты позволяют сформулировать
алгоритм построения
всевозможных частных решений, описывающих плоскопараллельную фильтра-
цию несжимаемой жидкости в однородных средах с прямолинейной анизотро-
пией и с произвольной ориентацией ГНА. 1). По полю ГНА и главным прони-
цаемостям вычисляем по формуле (1.3.6) компоненты тензора проницаемости.
При этом оси х и у располагаем в плоскости течения (в подошве (кровле) плос-
копараллельного слоя). 2). По формулам (3) и (5) записываем выражение для
комплексного переменного
Y
c
bac
iY
c
b
X
2
⋅
−
⋅+⋅−=ζ . (13)
3). Выбираем при решении обратных задач (или вычисляем при решении
прямых задач по заданным граничным условиям) некоторую аналитическую
функцию w(ζ) – комплексный потенциал течения, и по её действительной части
