Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах

Подождите немного. Документ загружается.

101

скважины практически не зависит от

l и его можно принять приближённо рав-

ным своему предельному при

∞

→l

значению – дебиту скважины в пласте с пря-

молинейной анизотропией. (Поэтому в таблице 3.2 и приведены подробно значе-

ния расчётов только для случая

3.1.3. Исследования точности методов интегрального и локального однородно-

анизотропного эквивалентирования в расчётах дебита центральной скважины в

слоистой среде.

Рассмотрим теперь расчёт дебита скважины в слоистой среде на рис. 9 и 10

методами локального и интегрального однородно-анизотропного эквивалентиро-

вания. На этом простом примере удобно подчеркнуть отличия в подходах назван-

ных методов и отметить их преимущества и недостатки.

Точные значения дебитов центральной круговой скважины на рис. 9 и 10 вы-

числяются по формулам:

(

)













⋅µ

−

⋅

CП2,1

точн

PP2

, (19)

где

1,2

– эффективные проницаемости слоистых областей на рис. 9 и 10 соответ-

ственно. Для слоистой среды из чередующихся изотропных круговых колец с

проницаемостями k

и k

на рис. 9 эффективная проницаемость

()

221

kkk

+−⋅δ

=Λ

, где

























⋅⋅

=δ

N2642

1N2753

rrrr

, (20)

- радиусы колец, r

= r

и R = r

2N+1

(когда в области фильтрации укладывается N

пар слоёв k

и k

) и R = r

2N+2

(когда в области фильтрации укладывается N пар и

один дополнительный слой с проницаемостью k

). Для среды из чередующихся

изотропных одинаковых по размерам круговых секторов с проницаемостями k

на рис. 10 эффективная проницаемость

102























++⋅

=Λ

)2(случаев,

1N2

)1(случаев,

, (21)

в которой в 1-ом случае в круговую область укладывается N пар секторов, а во 2-

ом –N пар и один дополнительный сектор с проницаемостью k

Слоистые среды на рис. 9 и 10 естественно моделировать радиально-

анизотропными, у которых ГНА направлены по координатным линиям полярной

системы координат. Дебит скважины Q

аниз

в среде с радиальной анизотропией вы-

числяется по формуле (18). Желая, чтобы радиально-анизотропная модель слои-

стых сред при расчёте дебита центральной скважины приводила к точному ре-

зультату, подберём

в (18) так, чтобы значения Q по формулам (18) и (19) совпа-

дали. Сравнивая (18) и (19), для

получим значение, совпадающее с

1,2

. Описан-

ный сейчас подход, предлагаемый автором для определения главной проницаемо-

сти λ

= Λ

1,2

, носит название метода интегрального однородно-анизотропного эк-

вивалентирования. Из изложенного в иллюстративном примере ясно, что предло-

женный метод в задачах эквивалентирования всегда приводит к точным результа-

там при любом числе слоёв и любом законе изменения их толщин. Это объясняет-

ся тем, что расчёт главных проницаемостей λ

1,2

в этом методе выполняется не для

структурной ячейки ω в её локальных декартовых координатах, а для всей много-

слойной области в целом, в системе координат, координатные линии которой сов-

падают как с границами раздела чередующихся слоёв многослойной среды, так и с

границами области, для которой осуществляется анизотропное эквивалентирова-

ние. В результате для λ

1,2

получаются значения, совпадающие с эффективными

проницаемостями

1,2

в точных решениях задач эквивалентирования. Недостатком

метода интегрального однородно-анизотропного эквивалентирования, значитель-

но ограничивающим область его применения, является то, что координатные ли-

нии выбираемой системы могут совпадать с границами раздела слоёв, но не сов-

103

падать с границами расчётной области. В этом случае расчёт главных проницае-

мостей анизотропной модели неизбежно приходится выполнять по методу ло-

кального однородно-анизотропного эквивалентирования.

Кристаллофизический метод локального однородно-анизотропного эквива-

лентирования для сред из чередующихся изотропных слоёв k

, k

с одинаковыми

толщинами h для главных проницаемостей

1,2

перпендикулярно к слоям и вдоль

слоёв приводит к значениям, получающимся из (1.1.14) при h

= h

= h и равным

kk2

=λ

. (22)

В соответствии с формулами (22) для рис.9 λ

= λ

, а для рис. 10 λ

= λ

. Результа-

ты относительных погрешностей

точн

анизточн

−

(в %) расчётов дебита методом ло-

кального однородно-анизотропного эквивалентирования для рис.9 приведены в

таблице 3.3, а для рис.10 – в таблице 3.4.

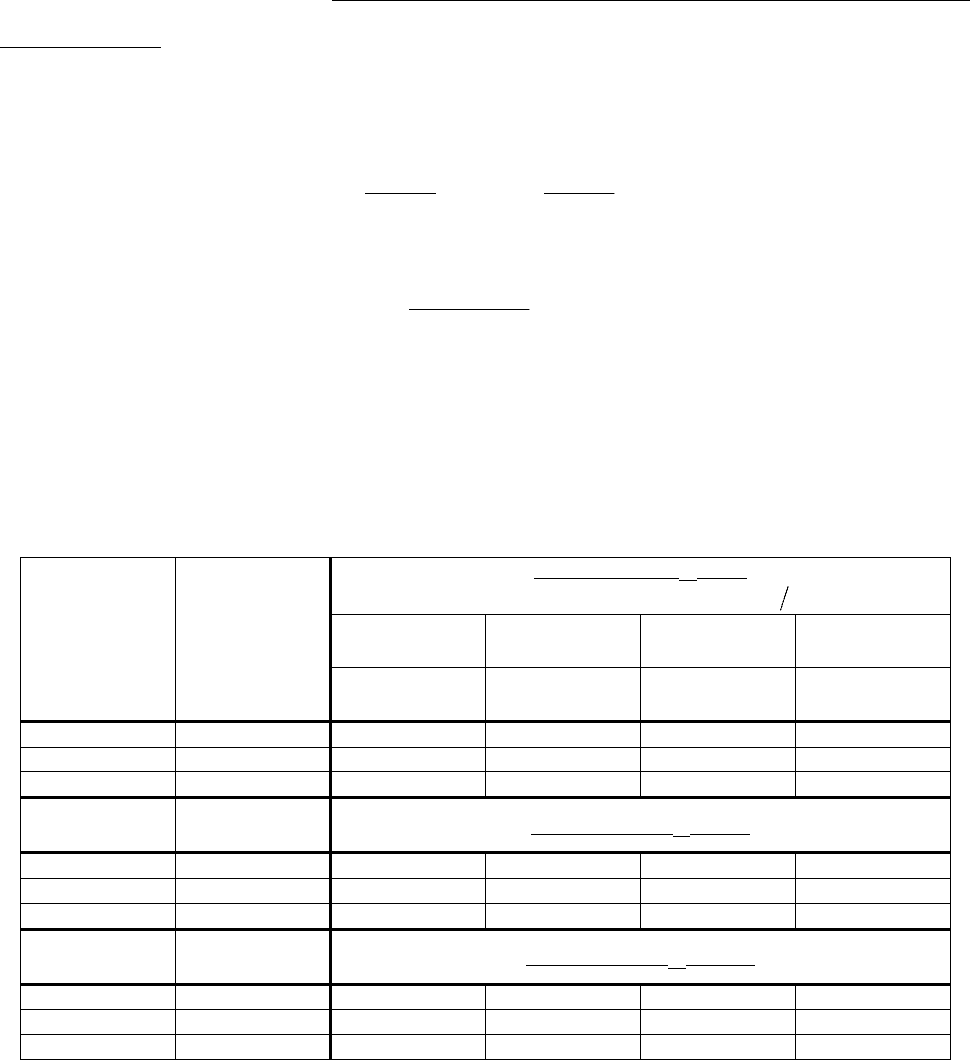
Таблица 3.3

Относительные погрешности (в %) расчётов дебита скважины на рис.9 методом локального од-

нородно-анизотропного эквивалентирования

1 –ый случай: R/r

скв

= 100

Отношение проницаемостей

kk=

2,00 10,00 20,00 100,00

Число слоёв

Отношение

h/r

скв

0,50 0,10 0,05 0,01

100

0,9900

±3,20 ±7,87 ±8,70 ±9,42

500

0,1980

0,70

1,73

1,91

2,07

50000

0,0020

0,01

0,02

Число слоёв

Отношение

h/r

скв

2 –ой случай: R/r

скв

= 1000

1000

0,9990

±2,17 ±5,34 ±5,90 ±6,40

5000

0,1998

0,48

1,17

1,30

1,41

50000

0,0200

0,05

0,12

0,13

0,14

Число слоёв

Отношение

h/r

скв

3 –ий случай: R/r

скв

= 10000

5000

1,9998

±2,83 ±6,96 ±7,69 ±8,33

10000

0,9999

1,63

4,01

4,44

4,80

100000

0,10000

0,18

0,44

0,49

0,53

(Знаки «+» соответствуют значениям ε= 2; 10; 20 и 100,

а знаки «–» - для ε = 0,50; 0,10; 0,05 и 0,01)

104

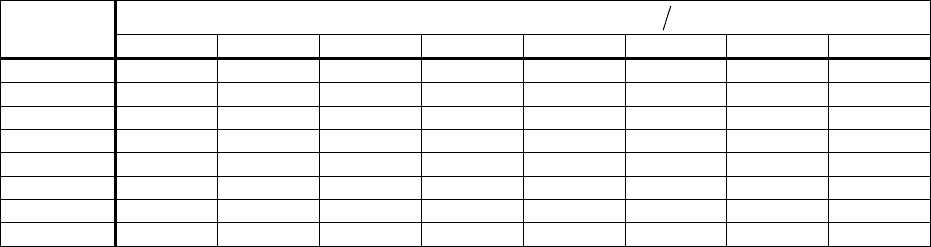
Таблица 3.4

Относительные погрешности (в %) расчётов дебита скважины на рис.10 методом локального

однородно-анизотропного эквивалентирования

Отношение проницаемостей

Число

секторов

0,01 0,05 0,10 0,50 2,00 10,00 20,00 100,00

7 -16,28 -14,84 -13,24 -5,00 4,55 10,47 11,45 12,28

11 -9,78 -8,96 -8,04 -3,13 2,94 6,92 7,60 8,18

21 -4,90 -4,50 -4,05 -1,61 1,56 3,75 4,13 4,46

51 -1,96 -1,81 -1,63 -0,66 0,65 1,58 1,74 1,89

101 -0,98 -0,90 -0,82 -0,33 0,33 0,80 0,89 0,96

501 -0,20 -0,18 -0,16 -0,07 0,07 0,16 0,18 0,20

1001 -0,10 -0,09 -0,08 -0,03 0,03 0,08 0,09 0,10

5001 -0,02 -0,02 -0,02 -0,01 0,01 0,02 0,02 0,02

Представленные результаты показывают медленную сходимость этого метода к

точному решению, которое практически достигается лишь тогда, когда в области

фильтрации укладывается не менее ~ 5·10

слоёв. В естественных условиях

толщины пропластков в слоистых средах могут составлять

≈

0,10

2,00 м, а харак-

терный размер области фильтрации ≈ 100÷5000 м. Поэтому число слоёв в реаль-

ных многослойных средах, как правило, изменяется в диапазоне

≈

⋅

, недос-

таточном для достижения высокой точности расчётов по кристаллофизическому

методу локального однородно-анизотропного эквивалентирования.

Таким образом, рассмотренный пример показывает, что для повышения точ-

ности фильтрационных расчётов в слоистых средах в случае возможности нужно

применять метод интегрального однородно-анизотропного эквивалентирования.

3.2. Обобщение фильтрационных теорем об окружности и прямой для анизо-

тропных сред

В этом параграфе фильтрационные теоремы об окружности и прямой, сфор-

мулированные в [41, 42] для кусочно-однородных изотропных сред, обобщаются

для сред со специальными видами криволинейной анизотропии. Полученные ре-

зультаты позволяют точно описать разнообразные фильтрационные течения в рас-

сматриваемых кусочно-однородных анизотропных средах, граница раздела кото-

рых представляет собой прямую или окружность. В большинстве же случаев при

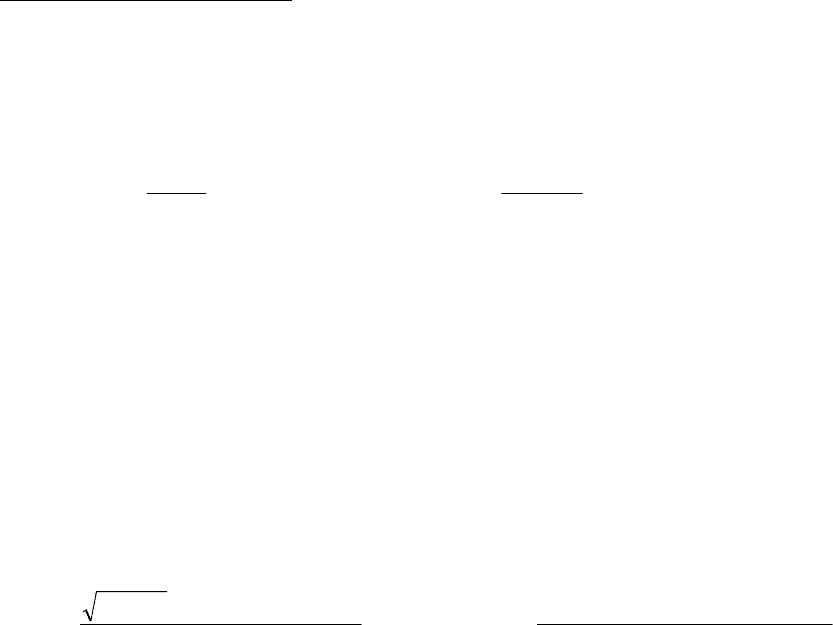
105

решении задач фильтрации в кусочно-однородных средах с криволинейной анизо-

тропией часто приходится ограничиваться приближёнными методами расчёта. Ре-

зультаты, полученные в данном параграфе, далее применяются в расчётах по

оценке точности метода локального однородно-анизотропного эквивалентирова-

ния слоистых сред. Кроме того, полученные результаты применены 1) к исследо-

ванию искажения плоскопараллельного поступательного потока в изотропной

среде круглым радиально-анизотропным включением, 2) к построению комплекс-

ного потенциала течения от источника в рассматриваемых кусочно-однородных

анизотропных средах и 3) к построению комплексного потенциала течения от ди-

поля в таких же средах.

3.2.1. Теорема об окружности.

Пусть плоскость xoy разделена окружностью

|z| = r

на две области, как показано на рис.16. В каждой области пористые среды

обладают своими центрально-симметричными законами распределения ГНА

(2.5.9), имеющими в полярных координатах r, θ вид

()

.2,1m;

,rq;dr

,rp

mmm

=θ⋅α+

Η⋅

⋅β=θθ⋅β−

⋅α=θ

∫∫

, (1)

и главными проницаемости

вдоль q

= const и p

= const соответст-

венно. В этом случае плоскопараллельное течение жидкости описывается двумя

комплексными потенциалами

(

)

(

)

)Z(w,ri,r

1111

⋅

()

(

)

)Z(w,ri,r

2222

ψ⋅+θϕ ,

аргументы Z

и Z

в которых в соответствии с (2.5.11) и (2.5.12) вычисляются по

формулам

(

)

(

)

2,1m;erRZ

,ri

=⋅=

θω⋅

(2)

в которых

()

(

)

[]

()

[]

()

()( )

()

[]

∫∫

λ⋅β+λ⋅Ηα⋅

⋅λ−λ⋅Η⋅β⋅α

−θ=θω













λ⋅β+λ⋅Ηα⋅

⋅β+Η⋅αλλ

⋅=

mm1

m1m2mmm

mm1

mm2m1

drr

,r;

drr

exprrR

На границе раздела кусочно-однородных анизотропных сред должны выпол-

няться условия непрерывности давления и нормальной составляющей скорости

106

фильтрации. Эти граничные условия через действительные и мнимые части ком-

плексных потенциалов согласно (2.5.17) записываются в виде:

при

:rr ψ=ψ

= , где .2,1m,K

m2m1m

=λλ= (3)

В случае рассматриваемых кусочно-однородных сред с центрально-

симметричной анизотропией потенциал

)Z(w

, описывающий искаженный круг-

лым включением r < r

фильтрационный поток, помимо (3) должен удовлетворять

также дополнительному условию на бесконечности. Например, если речь идет об

искажении круглым включением потока от особенностей (источников, стоков, ди-

полей), расположенных вне включения, то требуется, чтобы на бесконечности

распределение скоростей от

)Z(w

совпадало с распределением скоростей неис-

каженного течения.

Для кусочно-однородных сред с центрально-симметричной анизотропией (1)

комплексные потенциалы

)Z(w

и )Z(w

, удовлетворяющие (3), как легко прове-

рить, имеют вид

)Z(G)Z(F

)Z(w

);Z(G

)Z(F)Z(w

111













−













−

, (4)

где

)Z(F

и )Z(G

- аналитические функции, первая из которых имеет особые

точки вне окружности |z| = r

, а вторая - внутри неё, черта - знак комплексного со-

пряжения. Если характеристики анизотропных сред в областях 1 и 2 совпадают, то

KK = и ZZZ

= . Поэтому из (4) получим, что )Z(G)Z(F)Z(w)Z(w

== . Сле-

довательно, гидродинамический смысл функций

)Z(F и )Z(G состоит в том, что их

сумма

)Z(G)Z(F + представляет собой комплексный потенциал неискаженного

круглым включением фильтрационного потока от особенностей, расположенных

вне и внутри окружности |z| = r

. Отметим ещё, что комплексный потенциал )Z(w

из (4), в чем легко убедиться в каждом конкретном случае, удовлетворяет на бес-

107

конечности условию естественного для существа задачи характера. В частности,

если функция G=0 (поток создается особенностями, расположенными вне включе-

ния), то скорость на бесконечности искаженного потока

)Z(w

совпадает со ско-

ростью неискаженного потока. Наконец, отметим, что в частном случае, когда

1)r(H ≡ , формулы (4) дают ранее полученный в [45] результат. Для кусочно-

однородных изотропных сред (4) переходят в фильтрационную теорему

О.В. Голубевой об окружности.

3.2.2. Теорема о прямой.

Пусть плоскость xoy разделена прямой y = 0 на две

области y > 0 и y < 0, как показано на рис.17. В каждой области пористые среды

обладают своими конгруэнтными законами распределения ГНА (2.5.7), имеющи-

ми в декартовых координатах x, y вид

() () ()

()

2,1m;

xy,xq;dyyxy,xp

mmmmmmm

⋅α+⋅β=Η⋅β−⋅α=

∫∫

, (5)

и главными проницаемостями λ

, λ

вдоль q

= const и p

= const соответст-

венно. Плоскопараллельное течение жидкости описывается двумя комплексными

потенциалами

()

(

)

)(wy,xiy,x

1111

ψ⋅+

(

)

(

)

)(wy,xiy,x

2222

⋅

, аргументы

= ξ

+ i⋅η

(где m = 1,2) в которых в соответствии с (2.5.8) вычисляются по

формулам

()

(

)

()

(

)

[]

()

∫∫

λ⋅Η⋅β+λ⋅α

Η⋅β+α⋅λλ

=η

λ⋅Η⋅β+λ⋅α

λ−λ⋅Η⋅β⋅α

+=ξ

mm2

mm2m1

mm2

m2m1mmm

;dy

. (6)

Для кусочно-однородных сред с конгруэнтной анизотропией (5) комплексные

потенциалы

)(w

и )(w

, удовлетворяющие при y = 0 условиям (3), как легко

проверить, имеют вид

,)(G

)(G)(F

)(w

);(G

)(F

)(F)(w

111

−

+ζ+ζ

=ζ

+ζ

−

+ζ=ζ

(7)

108

где )(F

и )(G

, m = 1,2 - аналитические функции, особые точки первой из

них расположены в верхней полуплоскости, а второй - в нижней. Если характери-

стики анизотропной среды в нижней полуплоскости совпадают с соответствую-

щими характеристиками среды в верхней полуплоскости, то

KK = и

Поэтому из (7) получим, что

)(G)(F)(w)(w

2211

. Следовательно, гидроди-

намический смысл функций

)(F

и )(G

в том, что их сумма )(G)(F

представ-

ляет комплексный потенциал неискаженного кусочной однородностью фильтра-

ционного потока от особенностей, расположенных в областях y > 0 и y < 0.

3.2.3. Примеры применения теорем.

В качестве примера применения обоб-

щённой фильтрационной теоремы об окружности исследуем искажения плоскопа-

раллельных фильтрационных течений в изотропной среде с проницаемостью k

круглым однородным радиально-анизотропным цилиндрическим включением с

радиусом r

. Главные проницаемости включения в трансверсальном и в радиаль-

ном направлениях обозначим как

соответственно. Для сред с ра-

диальной анизотропией в формулах (1)

= 1 и

= 0. Поэтому, согласно (2), пере-

менные

Z и

Z в изотропной и анизотропной частях области фильтрации будут

соответственно равны

r12

где,e

rZ,zreZ

≡

=ε⋅













⋅===

θ⋅

. (8)

Пусть заданный комплексный потенциал невозмущённого течения F(z) имеет

точечные особенности только за пределами круглого включения. Тогда G(z) = 0 и

комплексные потенциалы искажённого течения в изотропной среде w

(z) и в ани-

зотропном включении w

) найдутся через F(z) в соответствии с (4) и (8) по

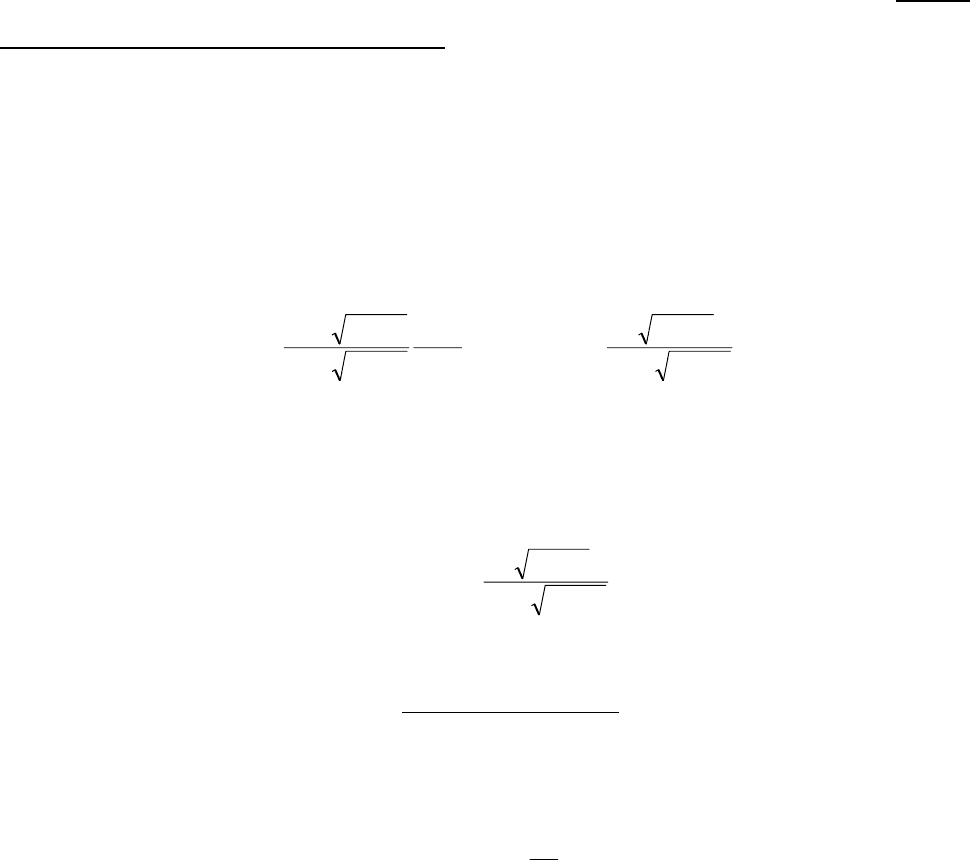
формулам

)Z(F

)Z(w;

)z(F)z(w

22120

2221

22120

⋅

λλ+

λλ













⋅

λλ+

λλ−

. (9)

109

Зная комплексные потенциалы (9), можно определить все интересующие нас

характеристики искаженного включением плоскопараллельного фильтрационного

течения. Например, величина фильтрационного потока Q

аниз

через диаметр AB

круглого анизотропного включения, совпадающий с осью y-ов, будет равна

)r,0()r,0(Q

0101аниз

−

. (10)

Пример 1. Применим формулы (9) и (10) к исследованию искажения посту-

пательного фильтрационного потока в однородной изотропной среде круглым

включением с радиусом r

и с радиальной анизотропией. Комплексный потенциал

)z(F неискаженного поступательного потока, двигающегося в положительном на-

правлении оси x со скоростью

∞

v , известен: zv)z(F

∞

. Подставляя )z(F в (9), най-

дем следующие комплексные потенциалы искажённого поступательного потока в

изотропной и радиально-анизотропной частях области фильтрации:

()

22120

2212

22120

Zw;

zv)z(w

∞

λλ+

λλ

λλ+

λλ−

. (11)

Пользуясь формулами (10) и (11), найдём поток Q

аниз

искаженного поступа-

тельного течения через диаметр АВ круглого радиально-анизотропного включе-

ния

22120

2212

аниз

Rv2Q

λλ+

λλ

⋅⋅=

∞

. (12)

Пример 2. В качестве другого применения результатов (9) рассмотрим ком-

плексные потенциалы течения от источника (стока).

Пусть источник располагает-

ся за пределами круглого включения на отрицательной части оси x-ов в точке с

полярными координатами

),b(

. Комплексный потенциал неискаженного включе-

нием течения от источника имеет вид

)bzln(

)z(F +

= . Подставляя )z(F в (9), по-

лучаем комплексные потенциалы течения от источника в изотропной среде и в ра-

диально-анизотропном включении в виде

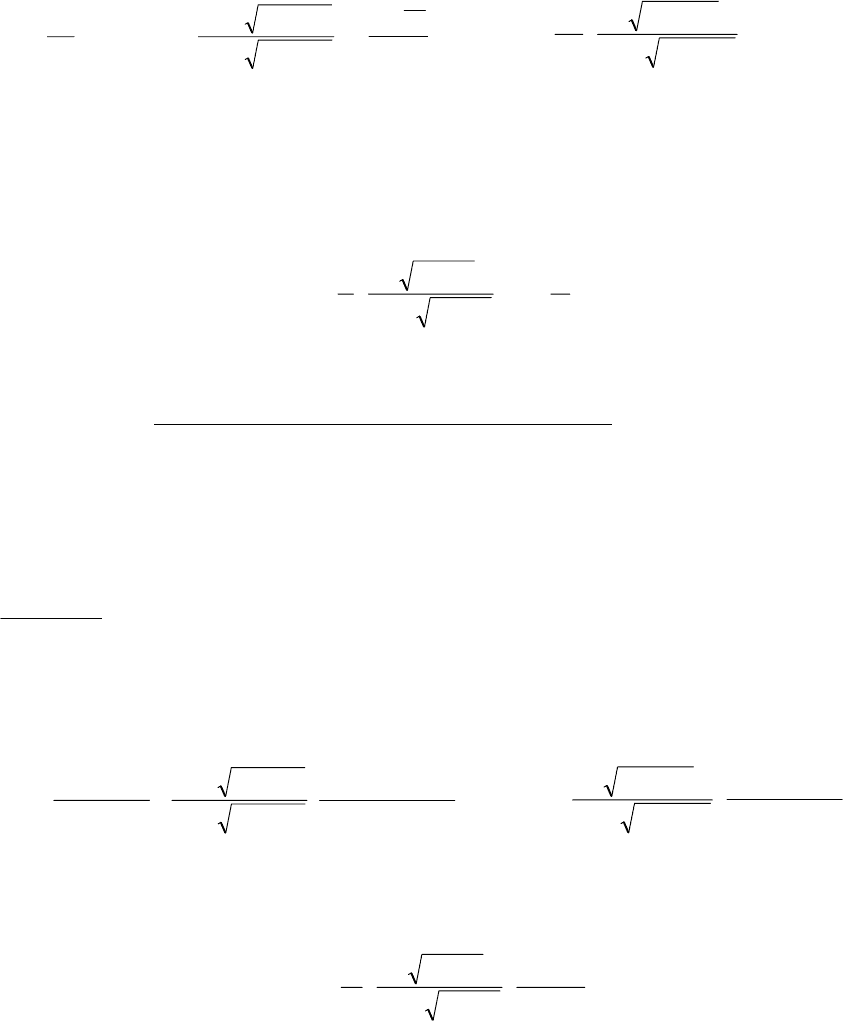
110













⋅

λ⋅λ+

λ⋅λ−

++⋅

)bzln(

)z(w

22120

()

bZln

)Z(w

22120

2212

+⋅

λ⋅λ+

λ⋅λ

⋅

= .(13)

Поток Q

аниз

искаженного течения от источника через диаметр АВ круглого

радиально-анизотропного включения в соответствии с (10) и (13) найдётся по

формуле

arctg

22120

2212

аниз

λλ+

λλ

⋅

. (14)

Пример 3. Применим ещё результаты (9) к построению комплексных потен-

циалов течения от диполя с действительным моментом m

в условиях двух преды-

дущих примеров. Пусть диполь располагается за пределами круглого включения

на отрицательной части оси x-ов в точке с полярными координатами

),b(

. Ком-

плексный потенциал неискаженного включением течения от диполя

()

bz2

)z(F

+⋅π

. Подставляя )z(F в (9), получаем комплексные потенциалы иссле-

дуемого течения от диполя в изотропной среде и в радиально-анизотропном

включении:

()

zbr2

bz2

)z(w

22120

⋅+⋅π

⋅

λ⋅λ+

λ⋅λ−

+⋅π

()

bZ2

)Z(w

22120

2212

+⋅π

⋅

λ⋅λ+

λ⋅λ

.(15)

Поток Q

аниз

искаженного течения от диполя через диаметр АВ круглого ради-

ально-анизотропного включения в соответствии с (10) и (15) найдётся по формуле

22120

2212

аниз

⋅

λλ+

λλ

⋅

−=

. (16)

В заключение подчеркнём, что область приложений результатов (4), (7) и (9),

конечно, не исчерпывается приведенными примерами.