Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.

71
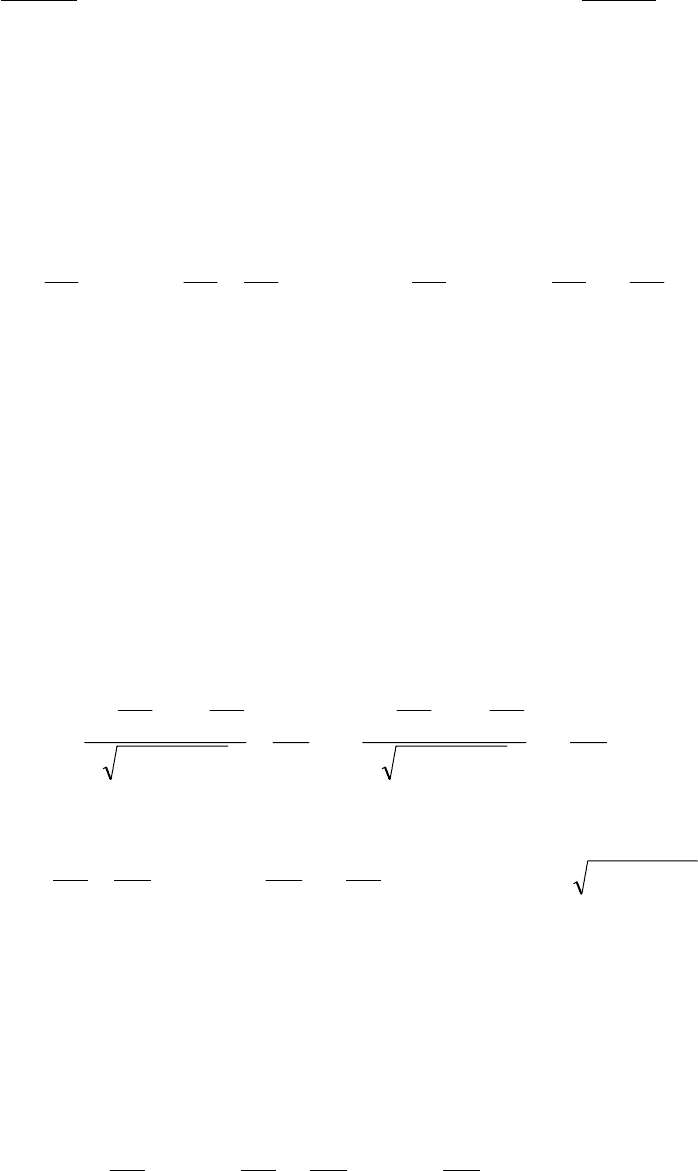
В уравнении (5) через Т
11
(ξ, η), Т
12
(ξ, η), Т
22
(ξ, η) обозначены выражения
()
∫∫∫
ζ
ζ
ζ
ζ
ζ
ζ
ζ
⋅
⋅
=ηξζ⋅=ηξζ
⋅
⋅
=ηξ
2
1
2
1
2
1
dk
H
HH
),(T;dkH),(T;dk
H
HH
),(T
22
2
31
221231211
1
32
11
, (6)
которые далее называем коэффициентами проводимости анизотропного искрив-
лённого пласта. При решении конкретных задач уравнение (5) ламинарной фильт-
рации несжимаемой жидкости в искривлённых анизотропных пластах переменной
толщины целесообразно рассматривать совместно с системой уравнений в частных
() () () ()
ξ∂
Ψ∂
−=
η∂
Φ∂
ηξ+
ξ∂
Φ
∂
ηξ
η∂
Ψ
∂
=
η∂
Φ
∂
ηξ+
ξ∂
Φ∂
ηξ ,T,T;,T,T
22121211
, (7)
что позволяет применять методы теории обобщённых аналитических функций
(И.Н. Векуа [28], L. Bers [234], L. Bers и A. Gelbart [235] и др.) к исследованию те-
чений в искривлённых слоях конечной толщины. Взаимосвязь уравнения (5) с сис-
темой уравнений (7) обнаруживается при перекрёстном дифференцировании сис-
темы, которое приводит к уравнению (5) для функции Φ(ξ, η). Если в (7) перейти к
новым переменным ξ
1
и η
1
, связанным с прежними ξ, η системой уравнений
Бельтрами [143, 157]
ξ∂
η∂
−=
−
η∂
ξ∂
+
ξ∂
ξ∂
η∂
η∂
=
−
η∂
ξ∂
+
ξ∂
ξ∂
1
2
122211
1
22
1
12
1
2
122211
1
12
1
11
TTT
TT
;
TTT
TT
, (8)
то (7) примет канонический вид
() ()
11
11
11
11
,p;,p
ξ∂
Ψ
∂
−=
η∂
Φ
∂
ηξ
η∂
Ψ∂
=
ξ∂
Φ∂
ηξ
, где
()
2
12221111
TTT,p −=ηξ (9)
системы для p-аналитической (по Г.Н. Положему [104, 105]) функции
Φ(ξ
1
,η
1
) + i⋅Ψ(ξ
1
,η
1
) = w(ζ
1
) комплексного переменного ζ
1
= ξ
1
+ i⋅η
1
. После пере-
крёстного дифференцирования системы (9) для функции Ф(ξ
1
, η
1
) получается сле-
дующее каноническое уравнение:
() ()
0,p,p
1
11
11
11
1
=
η∂
Φ∂
ηξ
η∂
∂
+
ξ∂
Φ∂
ηξ
ξ∂
∂
. (10)
Таким образом, в общем случае в плоскости вспомогательных переменных ξ
1
, η
1
течения в искривлённых анизотропных пластах описываются комплексными по-
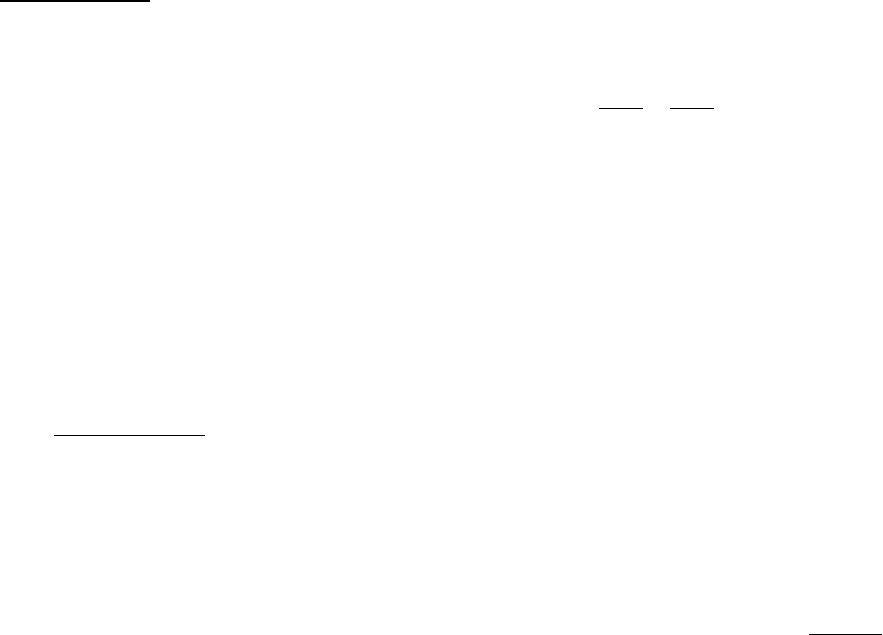
72
тенциалами w(ζ
1
), являющимися p-аналитическими функциями Г.Н.Положего
[104, 105].
Отметим теперь два важных следствия, вытекающих из (5), (6), (9) и (10).
Следствие 1.
Если выражение T
11
⋅T
22
− T
12
2
= const, то, как видно из (9) и (10), в
плоскости вспомогательного комплексного переменного ζ
1
= ξ
1
+ i⋅η
1
функция
Φ(ξ
1
, η
1
) будет удовлетворять уравнению Лапласа 0
2
1
2
2
1
2
=
η∂
Φ∂
+
ξ∂
Φ∂
. Поэтому во всех
тех частных случаях, когда T
11
⋅T
22
− T
12
2
= const, для описания линейной двумерной
фильтрации в таких слоях можно применять методы теории аналитических функ-
ций комплексного переменного. Далее приведены конкретные примеры таких сло-
ёв (это плоскопараллельные, сферические и круговые цилиндрические слои, за-
полненные однородной изотропной средой).
Следствие 2.
Рассмотрим теперь настолько тонкие искривлённые слои пере-
менной толщины (приближение О.В. Голубевой), в которых можно пренебречь
изменениями параметров Ламе по толщине слоя (по координате ζ) и принять их
равными своим значениям на подошве слоя, т.е.
12
13321221111
),(H
),,(HH);,(h),,(HH);,(h),,(HH
ζ−ζ
η
ξ
=ζηξ=ηξ=ζηξ=ηξ=ζηξ= . (11)
Значение третьего параметра Ламе
),,(H
13
ζ
η
ξ
в формулах (11) из соображений
геометрической наглядности выражено через длину
∫
ζ
ζ
ζζηξ=ηξ
2
1
d),,(H),(H
13
дуги ζ -
координатной линии, заключённой между кровлей и подошвой слоя. Поэтому ве-
личину
),(H ηξ в первом приближении можно рассматривать как толщину криво-
линейного слоя в точке
),( ηξ . Для выполнения условий (11) толщина пласта ),(H
η
ξ
в любой его точке должна быть намного меньше главных радиусов
кр1
R и
кр2
R кри-
визны подошвы и кровли слоя. О таких пластах, следуя О.В. Голубевой [41, 43],
будем говорить как о бесконечно тонких.
Пусть для бесконечно тонкого искривлённого слоя переменной толщины
),(H ηξ выполнены условия (11) и, кроме того, компоненты тензора проницаемости
k
ij
не зависят (т.к. слой бесконечно тонкий) от ζ. Тогда после подстановки пара-

73
метров Ламе из (11) в формулы (6) для коэффициентов проводимости искривлён-
ного бесконечно тонкого пласта получим значения:
()
()
() () () ()
()
()
() ()
ηξ⋅ηξ⋅
ηξ
ηξ
=ηξ⋅ηξ=ηξ⋅ηξ⋅
ηξ
η
ξ
= ,k,H
,h
,h
T;,k,HT;,k,H
,h
,h
T
22
2
1
22121211
1
2
11
. (12)
После подстановки (12) в (5) для Φ(ξ, η) получим уравнение
0kH
h
h
kHkHkH
h
h
22
2
1
121211
1
2
=
η∂
Φ∂
⋅⋅⋅+
ξ∂
Φ∂
⋅⋅
η∂
∂
+
η∂
Φ∂
⋅⋅+
ξ∂
Φ∂
⋅⋅⋅
ξ∂
∂
. (13)
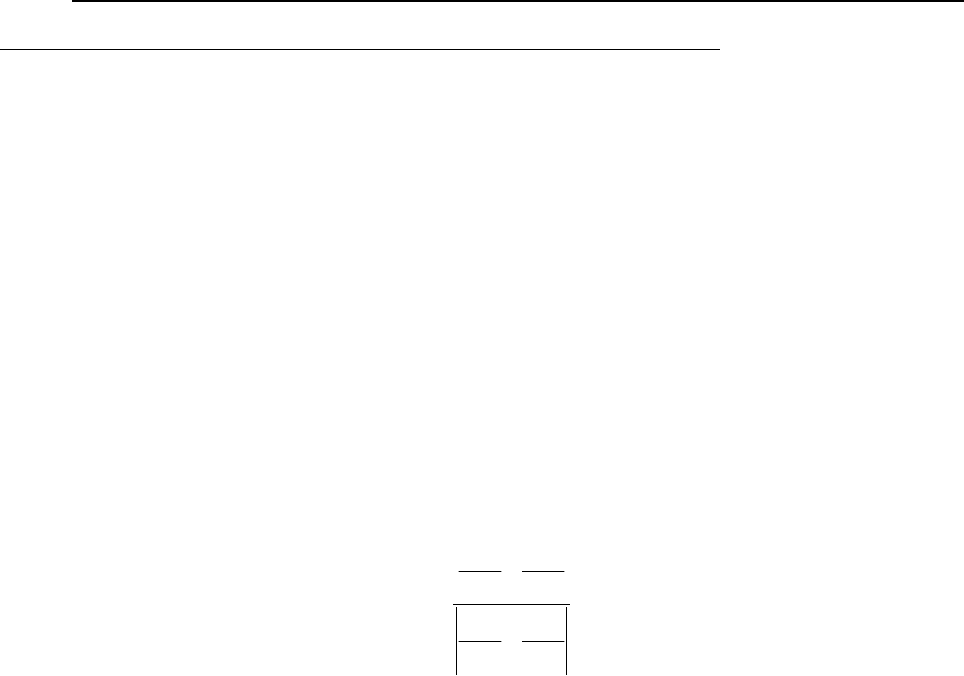
Заметим, что из формул (12) вытекает следующее равенство:
T
11
⋅T
22
− T
12
2
= H
2
⋅(k
11
⋅k
22
− k
12
2
). Поэтому если 1) толщина искривлённого слоя по-
стоянна, H = const и 2) слой заполнен однородной анизотропной (в частности, од-
нородной изотропной (k
11
= k
22
= k = const, k
12
= 0)) средой, для которой k
11
⋅k
22
−
k
12
2
= const, то тогда T
11
⋅T
22
− T
12
2
= const, и на основании следствия 1 приходим к
выводу: двумерные течения в любом бесконечно тонком однородном анизотроп-
ном (в частности, изотропном) искривлённом слое постоянной толщины описыва-
ются аналитическими функциями комплексного переменного.
В работах самой О.В. Голубевой и её учеников рассматривались бесконечно
тонкие неоднородные изотропные слои с переменной толщиной, причём на по-
дошве искривлённого слоя выбирались изотермические координаты, для которых
параметры Ламе h
1
и h
2
оказываются одинаковыми, т.е. h
1
= h
2
. Поэтому течения в
искривлённых изотропных бесконечно тонких слоях переменной толщины в тео-
рии О.В. Голубевой рассчитываются с помощью уравнения
() ()
0,p,p =
η∂
Φ∂
ηξ
η∂
∂
+
ξ∂
Φ∂
ηξ
ξ∂
∂
, (14)
которое вытекает как частный случай из (13) при h
1
= h
2
, k
12
= 0, k
11
= k
22
= k, и
p(ξ,η) = H(ξ,η)⋅k(ξ,η). Сравнивая (10) и (14), видим, что каноническое уравнение
(10) для Φ в предложенной уточнённой теории двумерных течений в искривлён-
ных анизотропных слоях конечной толщины и уравнение О.В. Голубевой (14) для
течений в бесконечно тонких изотропных искривлённых слоях имеют одинаковый
вид. Тем не менее между этими уравнениями большая разница, т.к. уравнение (10)
записано для вспомогательных переменных и для искривлённых анизотропных
7
4
слоёв конечной толщины, а (14) записано в координатах физической области тече-
ния и для бесконечно тонких искривлённых изотропных слоёв.
Укажем ещё способ расчёта коэффициентов проводимости для анизотропных
искривлённых слоёв с постоянной конечной толщиной H.
2.2.2. Расчёт коэффициентов проводимости для двумерной фильтрации в анизо-
тропных искривлённых слоях постоянной конечной толщины.
Пусть подошва
1
F криволинейного слоя задана параметрически с помощью
ортогональных на ней координат
ξ
и
η
уравнением вида ),(RR
0
ηξ=
r
r
(рис.5).
Определение. Криволинейный слой будем называть слоем постоянной толщи-
ны, если его кровля
2
F представляет геометрическое место концов отрезков посто-
янной длины, отложенных на нормалях к подошве слоя
1
F (рис. 5).
В дифференциальной геометрии такие поверхности
1
F и
2
F называют парал-
лельными криволинейными поверхностями.
Для того чтобы получить уравнение кровли
2
F , предварительно находим ко-
ординаты вектора единичной нормали
n
r
к подошве
1
F по формуле
η∂
∂
×
ξ∂
∂
η∂
∂
×
ξ∂
∂
=
00
00
RR
RR
n
rr
r
r
r
. (15)
Радиус-вектор внутренней точки M криволинейного слоя, как видно из рис. 5, най-
дётся по формуле
nH),(R),,(R
0
r
r
r
⋅⋅ζ+ηξ=ζηξ , (16)
где
10 ≤
ζ
≤ . Уравнение (16) при 0
=
ζ
даст уравнение подошвы
1
F , а при 1
=
ζ
–
кровли
2
F слоя. Важно заметить, что для криволинейных поверхностей
1
F , относя-
щихся либо к поверхностям вращения, либо к цилиндрическим поверхностям,
формулы (15) и (16) приводят к ортогональным криволинейным координатам
ζ
ηξ ,, .
Приведём конкретные примеры расчёта коэффициентов проводимости для
двумерной фильтрации в слоях постоянной толщины.

75
Пример 1. Слои вращения. Поверхность вращения
1
F (когда ось вращения
совпадает с осью z) задаётся параметрически уравнением вида
k)(z)jsini(cos)(r),(R
0
r
r
r
r
⋅ξ+⋅η+⋅η⋅ξ=ηξ
. (17)
Геометрический смысл параметров
η
ξ
, и функций )(z),(r ξ
ξ
в уравнении (17) пока-
зан на рис. 6. С помощью формул (15), (16) и (17) находим следующие уравнения
связи между декартовыми x, y, z и криволинейными
ζ
η
ξ
,, координатами точек
слоя вращения постоянной толщины:
),(fz;sin),(fy;cos),(fx
211
ζ
ξ
=
η
⋅
ζ
ξ
=
η
⋅
ζ
ξ= , (18)
где
()()
ξ
′
+ξ
′
=ξ
ξ
ξ
′
⋅⋅ζ
+ξ=ζξ
ξ
ξ
′
⋅⋅ζ
−ξ=ζξ
22
21
)(z)(r)(E
;
)(E
)(rH
)(z),(f;
)(E
)(zH
)(r),(f
. (19)
(Знаком «штрих» обозначено дифференцирование по ξ). Можно непосредственной
проверкой убедиться, что в области рассматриваемого слоя вращения постоянной
толщины H координаты
ζ
ηξ ,, ортогональны. С помощью формул (18) и (19) полу-
чаем следующие выражения для параметров Ламе:
)(E)(BH2)(AHH
222
1
ξ+ξ⋅⋅ζ+ξ⋅⋅ζ= constHH;),(fH;
312
==ζξ= , (20)
где
22
2
)(E
)(z
)(E
)(r
)(A
′
ξ
ξ
′
+
′
ξ
ξ
′
=ξ
,
′
ξ
ξ
′
⋅ξ
′
−
′
ξ
ξ
′
⋅ξ
′
=ξ
)(E
)(z
)(r
)(E
)(r
)(z)(B
. (21)
Теперь по формулам (6) можно будет вычислить коэффициенты проводимости
криволинейного слоя вращения постоянной толщины и записать затем конкретный
вид уравнения (5) для двумерной фильтрации в нём.
К примеру, когда подошва
1
F представляет собой сферу радиуса
1
R , функции
)(r ξ и )(z ξ в формуле (17) имеют вид ;sinR)(r
1
ξ
=
ξ
ξ
=
ξ
cosR)(z
1
. В соответствии с
(17)-(21) получаем, что
HH;sin)HR(H;HRH
31211
=
ξ
ζ
+
=
ζ
+
=
. Коэффициенты
проводимости для однородного изотропного сферического слоя постоянной тол-
щины H на основании (6) и (18)-(21), равны: ;sinHkT
11
ξ⋅
⋅
=
;0T
12
=
ξ
=
sin
kH
T
22
.

76
Уравнение (5) для однородного сферического изотропного слоя постоянной тол-
щины с найденными коэффициентами проводимости примет вид
0
sin
1
sin
2
2
=
η∂
Φ∂
⋅
ξ
+
ξ∂
Φ∂
⋅ξ
ξ∂
∂
. (22)
С помощью замены переменной ξ на
2
tgn
1
ξ
=ξ
l уравнение (22) сводится к уравне-
нию Лапласа
0
2
2
2
1
2
=
η∂
Φ∂
+
ξ∂
Φ∂
. Следовательно, для исследования всевозможных тече-
ний в однородных изотропных сферических слоях конечной толщины можно при-
менять методы теории аналитических функций комплексного переменного. В по-
давляющем большинстве других слоёв вращения постоянной конечной толщины
constTTT
2
122211
≠−⋅ , и поэтому необходимо будет применять для изучения в них
двумерной фильтрации методы теории обобщённых аналитических функций.
Пример 2. Цилиндрические слои постоянной толщины. В этих слоях (рис. 7)
образующие подошвы и кровли параллельны горизонтальной оси x декартовой
системы x, y, z (ось z направлена вертикально вверх). Параметрическое уравнение
)(r
0
α
r
линии пересечения подошвы 0
=
ζ
слоя с плоскостью yoz считаем заданным в
виде
k)(gj)(f)(r
0
r
r
r
α+α=α . (23)
Тогда радиус-векторы
),(r
ζ
α
r
точек слоя в плоскости yoz можно определить по
формуле (рис. 7)
nH)(r),(r
0
r
r
r
⋅
⋅
ζ
+
α=
ζ
α , где H – постоянная толщина слоя, n
r
– еди-
ничный вектор нормали к линии (23) и
ζ
– безразмерная координата, 10
≤
ζ
≤
. Ра-
диус-векторы
),,x(R ζα
r
любой точки цилиндрического слоя, сечение которого дано
на рис. 7, определим по формуле
),(rix),,x(R ζα+⋅=ζα
r
r
v
. Вычислив координаты
вектора
n
r
по формуле (15) (в которой полагаем ξ = x и η = α) и пользуясь двумя
последними формулами, для координат x, y, z точек рассматриваемого цилиндри-
ческого слоя следующие выражения:
)(E
)(f
H)(gz;
)(E
)(g
H)(fy;xx
α
α
′
⋅⋅ζ+α=
α
α
′
⋅⋅ζ−α==
, (24)

77
где
[][]
22
)(g)(f)(E α
′
+α
′
=α . (Штрих ' обозначает дифференцирование по α). С по-
мощью равенств (24) можно убедиться, что криволинейные координаты x, α, ζ ор-
тогональные. Для координат x, α, ζ параметры Ламе оказываются равными
1H
1
= , )(E)(BH2)(AHH
222
2
α+α⋅⋅ζ+α⋅⋅ζ= , constHH
3
== , (25)
где
22
2
)(E
)(g
)(E
)(f
)(A
′
α
α
′
+
′
α
α
′
=α
, .
)(E
)(g
)(f
)(E
)(f
)(g)(B
′
α
α
′
⋅α
′
−
′
α
α
′
⋅α
′
=α
(26)
Теперь с помощью найденных параметров Ламе по формулам (6) и (23)-(26) можно
вычислить коэффициенты проводимости цилиндрических слоёв постоянной тол-
щины.
Например, для кругового цилиндрического слоя
с радиусами подошвы и
кровли
1
R и
2
R и с толщиной
12
RRH
−
=
уравнение (23) имеет вид:
)kcosj(sinRr
10
rr
r
⋅α+⋅α= , угол α отсчитываем от оси z по ходу часовой стрелки. То-
гда в соответствии с (23), (25), (26) получим, что
HRH
12
⋅
ζ
+
=
. Поэтому для кру-
гового цилиндрического пласта постоянной толщины, заполненного однородной
изотропной (
constk = ) пористой средой, коэффициенты проводимости
1
T и
2
T в
соответствии с (6) оказываются равными следующим постоянным значениям:
)RR(k
2
1
T
2
1
2
21
−⋅= и
⋅=
1
2
2
R
R
lnkT
. Уравнение (5) для кругового однородного изо-
тропного цилиндрического слоя постоянной толщины примет вид
0T
x
T
2
2
2
2
2
1
=
α∂
ϕ∂
⋅+
∂
ϕ∂
⋅ . (27)
Если в (27) перейти к безразмерной переменной
x
T
T
x
1
2
1
⋅=
, то оно преобразуется
к уравнению Лапласа
0
x
2
2
2
1
2
=
α∂
ϕ∂
+
∂
ϕ∂
. Поэтому для описания двумерной фильтрации
в однородных круговых изотропных цилиндрических слоях постоянной толщины
могут быть применены методы теории аналитических функций комплексного пе-

78
ременного, чего нельзя сказать по отношению к произвольному цилиндрическому
слою постоянной конечной толщины.
2.3. Уравнения плоскопараллельных фильтрационных течений несжимаемой
жидкости в анизотропно-неоднородных средах и их связь с обобщёнными
аналитическими функциями комплексного переменного
В теории фильтрации важную роль в теоретическом и прикладном аспектах
играют плоскопараллельные фильтрационные течения, которые представляют ча-
стный случай описанных в §2.2 двумерных. Плоскопараллельные фильтрационные
течения жидкости существуют, если: 1) пласт ограничен плоскими параллельными
непроницаемыми подошвой (ζ = ζ
1
= 0) и кровлей (ζ = ζ
2
= Н, где Н – толщина
слоя), 2) одно из ГНА пористой среды в пласте всюду перпендикулярно к его по-
дошве (кровле) и 3) все компоненты тензора проницаемости K зависят лишь от ор-
тогональных координат ξ и η подошвы пласта.
Для ортогональных цилиндрических систем координат ξ, η, ζ (с перпендику-
лярной к подошве пласта осью ζ) параметры Ламе имеют вид:
() ()
HH;,GH;,EH
321
=ηξ=ηξ= , где E(ξ, η) и G(ξ, η)- коэффициенты 1-ой квад-
ратичной формы для ξ, η. Поэтому по формулам (2.6) для коэффициентов прово-
димости анизотропного неоднородного плоскопараллельного пласта получим сле-
дующие значения:
Hk
G
E
T;HkT;Hk
E
G
T
222212121111
⋅⋅=⋅=⋅⋅= . (1)
Система уравнений (2.7) с найденными коэффициентами (1) примет вид
ξ∂
Ψ∂
−=
η∂
Φ∂
⋅⋅⋅+
ξ∂
Φ∂
⋅⋅
η∂
Ψ∂
=
η∂
Φ∂
⋅⋅+
ξ∂
Φ∂
⋅⋅⋅ Hk
G
E
Hk;HkHk
E
G
22121211
, (2)
которую, однако, выгоднее переписать в другой, симметричной по отношению к
координатам ξ и η форме

79
ξ∂
ψ∂
−=
η∂
Φ∂
+
ξ∂
Φ∂
η∂
ψ∂
=
η∂
Φ∂
+
ξ∂
Φ∂
E
1
G
k
E
k
G
1
G
k
E
k
2212
1211
, где Ψ⋅=ψ
H
1
. (2′)
К этой же системе (2′) в рассматриваемом случае приводит сравнение проекций
скоростей фильтрации из тензорного закона Дарси (2.3)
η∂
Φ
∂
+
ξ∂
Φ
∂
=
η∂
Φ
∂
+
ξ∂
Φ∂
=
ηξ
G
k
E
k
v;
G
k
E
k
v
22121211
(3)
с таковыми же (1.14), выраженными через функцию тока течения ψ. Таким об-
разом, в случае плоскопараллельных течений предложенная в §2.2 общая тео-
рия двумерной фильтрации приводит к тем же результатам, что и классический
подход.
Система уравнений (2) (а значит и (2′)) приводится к каноническому виду
при помощи частных решений системы (2.8). После подстановки в (2.8) коэф-
фициентов проводимости (1) и тождественных преобразований система (2.8)
запишется в виде
ξ∂
η∂
⋅−=
η∂
ξ∂
⋅+
ξ∂
ξ∂
⋅
η∂
η∂
⋅=
η∂
ξ∂
⋅+
ξ∂
ξ∂
⋅
1
3
1221121
3
112111
E
I
G
k
E
k
;
G
I
G
k
E
k
, (4)
где I
3
– инвариант (1.3.8) тензора проницаемости
21
2
1222113
kkkI λ⋅λ=−⋅= . (5)
Система (2) путём перехода к новым переменным ξ
1
, η
1
, удовлетворяющим (4),
приводится к каноническому виду (2.9), который сейчас запишется следующим
образом:
11
3
11
3
IH;IH
ξ∂
Ψ
∂
−=
η∂
Φ
∂
⋅⋅
η∂
Ψ
∂
=
ξ∂
Φ
∂
⋅⋅ . (6)
Канонический вид системы уравнений (2′) немедленно вытекает из (6) после под-
становки в неё выражения связи Ψ=H⋅ψ, что приводит к следующей системе:
11
3
11
3
I;I
ξ∂
ψ
∂
−=
η∂
Φ
∂
⋅
η∂
ψ
∂
=
ξ∂
Φ
∂
⋅ . (6′)
Система уравнений (6′) совпадает с условиями p-аналитичности обобщён-
ных аналитических функций Г.Н. Положего [104, 105]. Таким образом, плоско-

80
параллельные фильтрационные течения в рассматриваемых анизотропных сре-
дах описываются p-аналитическими функциями с характеристикой
213
Ip λλ== . Заметим ещё, что систему (6′) можно трактовать как систему
уравнений, описывающую плоскопараллельные фильтрационные течения на
вспомогательной плоскости с декартовыми координатами ξ
1
, η
1
в неоднородной
изотропной среде с проницаемостью k, равной характеристике
213
Ip λλ== .
Целесообразность такой трактовки [144, 157, 168] замены независимых пере-
менных вытекает из того, что неортогональная сеть Φ = const, ψ = const течения
в анизотропном грунте переходит в ортогональную сеть на вспомогательной
плоскости ξ
1
, η
1
. Последнее позволяет строить гидродинамические сетки плос-
копараллельных течений в неоднородных анизотропных средах по ортогональ-
ным гидродинамическим сеткам сходных течений в неоднородных изотропных
средах с проницаемостью
213
Ik λλ== .
2.4. Уравнения плоскопараллельных фильтрационных течений несжимаемой
жидкости в анизотропно-однородных средах и их связь с аналитическими
функциями комплексного переменного
Снова, как и в §2.3, рассматриваем плоскопараллельные течения несжимае-
мой жидкости в анизотропных средах, в которых одно из ГНА всюду перпендику-
лярно к плоскости течения. Но в отличие от предыдущего §2.3 рассмотрим случай,
когда главные проницаемости λ
1
, λ
2
, λ
3
анизотропной среды постоянны. Тогда и
инвариант тензора проницаемости I
3
= k
11
k
22
– k
12
2
= = λ
1
λ
2
= const. С учётом этого
замечания систему уравнений движения (3.2′) можно представить в виде
ξ∂
ψ∂
−=
η∂
ϕ∂
+
ξ∂
ϕ∂
η∂
ψ∂
=
η∂
ϕ∂
+
ξ∂
ϕ∂
E
1
G
c
E
b
G
1
G
b
E
a
, (1)
в котором применены обозначения
(
)
1bca,заметим,причём,
k
c;
k
b;
k
a
2
21
22
21
12
21
11
≡−⋅
λλ
=
λλ
=
λλ
= (2)
