Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.

51
де круговых конусов, расположенных в вершинах структурной ячейки ω в виде
прямого параллелепипеда с квадратным основанием. Причём в любом конусе
вектор
l
r
, расположенный на его оси симметрии и направленный от основания
к вершине, сонаправлен с ортом
3
e
r
оси ζ′ перпендикулярной к основанию ячей-
ки. Пространство между «зёрнами» внутри ячейки пусть заполнено пористой
изотропной средой. Фигурой Ω, характеризующей симметрические свойства, в
этом примере будет правильная четырёхугольная пирамида. Ось ζ′ будет осью
симметрии 4-го порядка, а плоскости η′ζ′, ξ′ζ′ и диагональные сечения - плос-
костями симметрии фигуры Ω. Тензоры А и С, инвариантные относительно пе-
речисленных видов симметрии фигуры Ω, в системе ГНА имеют вид: у тензора
А не равны нулю только компоненты a
11
= a
22
= λ
1
, a
33
= λ
3
, а у тензора С от-
личными от нуля могут быть лишь компоненты c
1111
= c
2211
= c
1122
= c
2222
= p
1
;
c
3311
= c
3322
= p
2
; c
1133
= c
2233
= p
3
; c
3333
= p
4
, c
1212
= c
2112
= c
1221
= c
2121
= q
1
; c
1313
=
c
3113
= c
1331
= c
3131
= c
2323
= c
3223
= c
2332
= c
3232
= q
2
. У тензора В не равны нулю
только компоненты b
131
= b
311
= b
232
=b
322
= a и b
333
= b ≠ 0. ОЗД (4) для нели-
нейной фильтрации в этих средах в системе ГНА запишется в виде:
()
(
)
[
]
()( )
()
,evpvpvpv
evpvpvpvevpvpvpv
evbeveva2vevevev P
3
2
333
2
232
2
1313
2
2
323
2
222
2
12121
2
313
2
212
2
1111
332211333322111
r
rr
r
r
r
r
r
r
⋅++⋅+
+⋅++⋅+⋅++⋅+
+
⋅⋅+
+
⋅
⋅
+
λ
+
+⋅λ=∇−
(15)
где p
11
= p
22
= p
1
; p
12
= p
21
= p
1
+ 2q
1
; p
13
= p
23
= p
2
+ 2q
2
; p
31
= p
32
= p
3
+ 2q
2
; p
33
=
p
4
. Фильтрационное сопротивление рассматриваемой анизотропной среды
вдоль направления
v
v
n
v
r
= в соответствии с формулами (2) и (15) оказывается
равным
()
(
)
(
)
[
]
()( )( ){ }
vnpnpnpnnpnpnpnnpnpnpn
vnbnna2nnnnr
22
333
2
232
2
131
2
3
2
323
2
222
2
121
2
2
2
313
2
212
2
111
2
1
3
2
3
2
2
2
1
2
33
2
2
2
11
⋅+++++++++
+⋅⋅++⋅+λ++λ=
r
. (16)
Формула (16) показывает, что для течений в плоскости ξ′η′ фильтрационное
сопротивление одинаково для противоположных направлений. В частности, ес-
ли q
1
= 0, то плоскость ξ′η′ будет, согласно (16), плоскостью изотропии. Однако
52
для взаимно противоположных течений вдоль оси ζ′ фильтрационные сопро-
тивления r
+
и r
–
этой среды оказываются различными и соответственно равны-
ми
2
43
2
43
vpvbrиvpvbr ⋅+⋅−λ=⋅+⋅+λ=
−+
, (17)
где v = v
3
. Ранее теоретические обоснования асимметрии фильтрационных
свойств некоторых анизотропных сред приводились в [14, 49, 187]. Полученные
представления для ОЗД позволят исследовать фильтрационные эффекты, при-
сущие нелинейным режимам фильтрации в анизотропных средах, и установить
взаимосвязь с подходом С.Н. Нумерова.
1.5. Математическое моделирование нелинейной фильтрации в анизотроп-
ных средах обобщённым методом С.Н.Нумерова
Перейдём к построению моделей нелинейной фильтрации в анизотропных
средах обобщённым методом С.Н.Нумерова. В предыдущем §1.4 уже отмеча-
лось, что обобщение закона фильтрации в рамках предположения (4.1) подра-
зумевает разложение в ряд Тейлора по степеням v
i
(i = 1,2,3) функции F
r
в ок-
рестности
0v
r
r
= . Такое разложение в ортонормированном базисе с учётом ра-
венства
0vпри0F
v
r
r
r
== имеет вид (4.3). Если в правой части (4.3) вынести общий
множитель v
j
, то это разложение примет вид
jiji
vrP
=
∇
−
, (1)
где
K
ll
+
++= vvcvbar
kijkkijkijij
. Формула (1) показывает, что связь между
полями ∇Ρ и
v
r
как для линейной, так и для нелинейной фильтрации в анизо-
тропных средах в произвольном ортонормированном расчётном базисе
{}
321
e,e,e
v
v
v
аппроксимируется матричным уравнением одного и того же вида
VRP
⋅
=
∇
−
, (2)
где ∇P = (∇
1
P, ∇
2
P, ∇
3
P)
T
и V = (v
1
, v
2
, v
3
)
T
– одностолбцовые матрицы из коор-
динат ∇P и
v
v
, а компоненты матрицы
(
)
3
1j,i
ij
rR
=
= образуют тензор 2-го ранга, на-
зываемый тензором фильтрационных сопротивлений пористой среды. Чтобы
найти тензор R в произвольном ортонормированном базисе
{}
321
e,e,e
v
v
v
, надо
53
предварительно определить его компоненты
ij
r
′
в некотором исходном базисе
{}
321
e,e,e
′′′
v
v
v
- базисе из главных направлений анизотропии пористой среды.
В диссертации ограничиваемся рассмотрением только тех анизотропных
сред, ГНА у которых попарно ортогональны и известны априори. Примерами
таковых, в частности, служат трансверсально-изотропные и ортотропные среды
[16]. В базисе из ГНА уравнение (2) примет вид
V
r00
0r0
00r
P
33
22
11
′
⋅
′
′
′
=∇
′
−
. (3)
Компоненты r′
11
, r′
22
и r′
33
тензора R в формуле (3), определяющие фильтраци-
онные сопротивления вдоль ГНА, назовём главными фильтрационными сопро-
тивлениями среды (ГФС).
Для слоистых, трещиновато-пористых, армированных сред и для сред с
полярным ГНА в предыдущем §1.4 были указаны соответствующие варианты
записи ОЗД. В ГНА все полученные в §1.4 ОЗД имели один и тот же вид (3) и
отличались друг от друга только выражениями для ГФС среды. В первом при-
мере (4.12) для слоистых и трещиновато-пористых сред ГФС r′
11
, r′
22
и r′
33
среды
оказались равны
(
)
(
)
VDVr;VDVrr
3
T
3331
T
12211
⋅⋅+λ=
′
⋅⋅+λ=
′
=
′
, (4)
где
[]
[
]
43332111
p,p,pdiagD;p,p,pdiagD
=
= . Во втором примере (4.13) для пе-
риодических сред, представляющих композиты с взаимно-перпендикулярными
направлениями армирования, r′
11
, r′
22
и r′
33
оказались равны значениям
(
)
,3,2,1i;VDVr
i
T
iii
=⋅⋅+λ=
′
(5)
в которых матрицы D
i
тоже имеют диагональный вид. В третьем примере
(4.15) для среды с кубической структурной ячейкой и с полярным ГНА
3
e
r
ГФС
среды оказались равны
(
)
(
)
VDVe,vcr
i
T
3iiii
⋅⋅+⋅+λ=
′
r
r
, (6)

54
где
=
=
=
=λ
=λ
=λ
3i если , b
1,2 i если , a2
c;
3 i если ,
1,2i если ,
i
3
1
i
, а D
i
= diag [p
i1
,p
i2
,p
i3
] для i = 1,2,3. В
формулах (4)–(6) через λ
1
, λ
2
, λ
3
, a, b, c, p
1
, p
2
, p
3
обозначены некоторые число-
вые параметры, а через D
1
, D
2
, D
3
- диагональные матрицы, характеризующие
фильтрационные свойства элементарных структурных ячеек названных сред.
Эвристическое значение ОЗД (4)-(6), полученных в §1.4 состоит в том, что они
позволяют выдвинуть гипотезу о строении тензора R в системе ГНА. Сформу-
лируем её в виде предложения 1.
Для всех анизотропных (периодических) сред
со структурной ячейкой
ω
в виде прямоугольного параллелепипеда обобщённый
закон Дарси нелинейной фильтрации в системе координат ГНА можно пред-
ставить в виде (3). Главные фильтрационные сопротивления
332211
r,r,r
′
′′
в (3) при-
нимают только положительные значения и представляют собой функции
(
)
(
)
(
)
=
⋅⋅µ=
′
3,2,1i
VDV,n,v,v,,Mfr
i
T
kiii
r
r
, (7)
зависящие от координат точки наблюдения М, коэффициента динамической
вязкости
µ
и от инвариантных величин: модуля vv
r
= вектора скорости
фильтрации; скалярных произведений
(
)
k
n,v
r
r
вектора v
r
с некоторыми задан-
ными векторами
k
n
r
и от квадратичных форм (V
T
⋅
D
i
⋅
V). (Условия r
′
ii
> 0 для
всех i = 1,2,3 продиктованы необходимостью выполнения неравенства
()
0v,P <∇
r
в каждой точке области фильтрации).
Приведённые примеры показывают, что функции (7) можно задавать в ви-
де:
(
)
(
)
(
)
()
=
⋅⋅+⋅µ+µλ=
′
∑
3,2,1i
VDVn,vv,,Mbv,,Mr
i
T
k
m
kikiii
k
r
r
. (8)
Сделаем некоторые замечания к формулам (7) и (8). В предлагаемой математи-
ческой модели фильтрационные свойства пористой анизотропной среды в глав-
ных чертах определяются заданием: 1) ГНА, 2) направлений особых фильтра-
ционных свойств
k
n
r
(НОФС), 3) скалярных функций λ
i
(M,µ,v) и b
ik
(M,µ,v) и 4)
положительно определённых квадратичных форм (V
T
⋅D
i
⋅V). Функции λ
i
(M,µ,v)
55
принимают положительные значения, а b
ik
(M,µ,v) – знакопостоянные. Первые
слагаемые λ
i
(M,µ,v) позволяют учесть зависимость ГФС пористой среды от
пространственных координат и от модуля скорости фильтрации. Вторые
сла-
гаемые
()()
∑
⋅µ
k
m
kik
k
n,vv,,Mb
r
r
позволяют учесть возможность наличия одного
или нескольких НОФС пористой анизотропной среды. Причём в общем случае
НОФС могут и не совпадать с ГНА. Если для течений вдоль орта
k
n
r
наблюда-
ется асимметрия
фильтрационных свойств анизотропной среды, то показатель
степени m
k
выбирается нечётным, а функции b
ik
(M,µ,v) > 0 будут определять
различие фильтрационных сопротивлений в противоположных направлениях.
Если для течений в направлении орта
k
n
r
фильтрационные сопротивления могут
принимать экстремальные
значения, то степени m
k
выбираются чётными. При
этом, если вдоль
k
n
r
ГФС достигают максимальных значений, то тогда функции
выбираются b
ik
(M,µ,v) > 0. Если же вдоль
k
n
r
ГФС минимальны, тогда функции
b
ik
(M,µ,v) < 0. Наконец, если направлений с особыми фильтрационными свой-
ствами нет, то функции b
ik
(M,µ,v) = 0. Третьи слагаемые (V
T
⋅D
i
⋅V) в (8) - поло-
жительно определённые квадратичные формы от координат вектора скорости
фильтрации. Собственные числа симметричных матриц D
i
тоже могут зависеть
от скалярных аргументов М, µ и v. С помощью выбора матриц D
i
можно учесть
какие-то дополнительные симметрические свойства порового пространства, ко-
торые нельзя определить одним лишь заданием ГНА.
Первое обобщение нелинейной фильтрации на анизотропные грунты,
предложенное С.Н.Нумеровым в [96, 250], из (7) и (8) получается как частный
случай, когда все D
i
= 0, b
ik
= 0, а λ
i
= a
i
+ b
i
⋅v.
Если уравнение (2) переписать в виде, разрешённом относительно компо-
нент скорости фильтрации, то придём к обобщённому закону Дарси, по форме,
совпадающей с (3.9). Поэтому (3.9) можно применять не только для описания
линейной, но и нелинейной фильтрации в рассматриваемом классе анизотроп-
ных сред. Однако в случае нелинейной фильтрации главные проницаемости λ
i
нужно считать, по аналогии с ГФС r′
11
, r′
22
и r′
33
, функциями вида

56
()
(
)()
3,2,1i,VDV,n,v,v,Mf
~
i
T
kii
=⋅⋅=λ
r
r
со всеми теми же замечаниями к ним, кото-
рые делались к формулам (7) и (8).
Преимущество предлагаемого обобщённого метода С.Н. Нумерова: 1) его
применение не требует решения сложной задачи построения тензоров высших
рангов, отвечающих заданной точечной группе симметрии. Вместо неё решает-
ся более простая задача – построение симметричного в ортонормированном ба-
зисе тензора второго ранга по заданному полю ГНА. Решение последней авто-
ром дано в [166, 170, 188, 189, 196, 209]; 2) предлагаемый способ позволяет све-
сти расчёт фильтрации к решению краевой задачи для одного нелинейного
уравнения. В случае применения ОЗД, предлагаемых Н.М. Дмитриевым [51],
расчёт фильтрации сводится, как правило, к интегрированию системы нелиней-
ных уравнений; 3) если расчётная система координат не совпадает с ГНА, то
для перехода в неё в предлагаемом методе нужно пересчитывать лишь тензоры
2-го ранга. Если же применять математические модели [51], то кроме тензоров
2-го ранга нужно пересчитывать ещё и тензоры 3 и 4-го рангов по более слож-
ным и громоздким формулам.
1.6. Пример построения математической модели нелинейной фильтрации в
анизотропной среде обобщённым методом С.Н. Нумерова
В качестве конкретного примера применения обобщённого метода
С.Н. Нумерова предложим математическую модель плоскопараллельной
фильтрации в среде с прямолинейной анизотропией и с полярным ГНА. Вдоль
ГНА этой среды направим оси x, y и z. Пусть плоскость течения совпадает с
xoy, а ось x-ов будет осью с особыми фильтрационными свойствами (например,
она может быть полярной). Поэтому орт, задающий ГНА с особыми свойства-
ми, совпадает с осью x-ов, и, следовательно,
(
)
(
)
x
vi,vn,v ==
r
r
r
r
. Для конкретизации
математической модели функции f
i
в (5.7) зададим равенствами
()
⋅
µ
=
⋅
µ
=
′
=
′
v
v
fk
v
n,v
fk
rr
x
2211
r
r
, (1)

57
где под µ подразумевается динамическая вязкость жидкости, а k – постоянная с
размерностью проницаемости. Сделанный в (1) выбор функций (5.7) позволяет
записать ОЗД (5.3) нелинейной фильтрации в рассматриваемой среде в виде
µ
⋅
−=ϕϕ∇⋅
=
Pk
где,
v
v
fv
x
r
. (2)
Формула (2) показывает, что рассматриваемая среда с прямолинейной анизо-
тропией обладает следующими свойствами. Во-первых, в этой анизотропной
среде векторы
v
r
и ∇ϕ всегда коллинеарны. Во-вторых, проницаемость среды,
равная
⋅
v
v
fk
x
, зависит от угла θ, который составляет скорость фильтрации v
r
с положительным направлением полярного ГНА. В-третьих, полярное ГНА
может проявлять асимметрию свойств, т.к. для положительного и отрицатель-
ного направлений оси x-ов проницаемости k⋅f(1) и k⋅f(-1) могут и не совпадать.
Запишем уравнения плоскопараллельной фильтрации в такой прямолиней-
но-анизотропной среде в декартовых координатах. Для этого сравним проекции
скорости v
x
и v
y
из (2) с таковыми же, выраженными через функцию тока ψ, ко-
торую обычным образом [16, 85, 86, 102] можно ввести в рассмотрение на ос-
новании уравнения неразрывности
0vdiv
=
r
. В результате получим следующую
систему:
xyv
v
fv;
yxv
v
fv
x
y
x
x
∂
ψ∂
−=
∂
ϕ∂
⋅
=
∂
ψ∂
=
∂
ϕ∂
⋅
=
. (3)
Система уравнений (3) нелинейная, но она позволяет провести исключение од-
ной из функций и свести задачу к интегрированию уравнения для другой функ-
ции. Для исключения ψ заметим, что
()
yx
2
y
2
x
xx
,f
v
v
f ϕϕΦ=
ϕ+ϕ
ϕ
=
, где ϕ
x
и ϕ
y
–
соответствующие частные производные. Выполняя в (3) перекрёстное диффе-
ренцирование, для функции ϕ получим нелинейное уравнение
() ()
0
y
,
yx
,
x
yxyx
=
∂
ϕ∂
⋅ϕϕΦ
∂
∂
+
∂
ϕ∂
⋅ϕϕΦ
∂
∂
. (4)

58
Для исключения ϕ введём в рассмотрение функцию
()
=ψψ
v
v
f
1
,F
x
yx
, где
2
y
2
x
y
x
v
v
ψ+ψ
ψ
=
, а через ψ
x
и ψ
y
обозначены соответствующие частные производ-
ные. Тогда после перекрёстного дифференцирования системы (3) для функции
тока получим нелинейное уравнение
() ()
0
y
,F
yx
,F
x
yxyx
=
∂
ψ∂
ψψ
∂
∂
+
∂
ψ∂
ψψ
∂
∂
. (5)
Частные решения уравнений (4) и (5) описывают все плоскопараллельные тече-
ния в рассматриваемой анизотропной среде. Например, частным решением
уравнения (5) выступает, как легко проверить, функция ψ(x, y) = v
x
⋅y - v
y
⋅x + C,
где v
x
, v
y
и C – произвольные постоянные, характеризующие поступательный
фильтрационный поток со скоростью
jvivv
yx
r
r
r
⋅+⋅= .
Два других точных решения системы (3) можно найти, если в ней перейти
к полярным координатам r и θ. В полярных координатах (3) принимает вид
rr
v
v
f
v;
r
1
rv
v
fv
x
x
r
∂
ψ∂
−=
θ∂
ϕ∂
⋅
=
θ∂
ψ∂
⋅=
∂
ϕ∂
⋅
=
θ
. (6)
С помощью (6) можно найти точное решение классической задачи о дебите
центральной скважины в круговом пласте для рассматриваемой анизотропной
среды. Допуская существование плоско-радиального течения к такой скважине,
мы должны считать v
x
= v⋅cos(θ) и, следовательно,
()
θ=
cosf
v
v
f
x
. Трансвер-
сальная составляющая v
θ
в радиальном течении отсутствует, поэтому, согласно
второму уравнению системы (6), функции ϕ и ψ будут зависеть только от одной
переменной, а именно ϕ = ϕ(r) и ψ = ψ(θ). Тогда из (6) находим, что
(
)
(
)
(
)
DdcosfA;CrnAr +θ⋅θ⋅=θψ+⋅=ϕ
∫
l , (7)
где A, C и D – произвольные постоянные. Удельный дебит Q добывающей
скважины равен
()
∫∫
ππ
θ⋅θ⋅−=θ⋅⋅−=
2
0
2
0
r
dcosfAdrvQ
. (Знак «минус» поставлен ввиду

59
отрицательного знака проекции v
r
). Если на контуре скважины r=r
c
и на круго-
вой границе r = R области питания будут, как обычно, заданы значения приве-
дённого давления P
C
и P
П
соответственно, то с помощью (7) окончательно най-
дём, что
(
)
⋅µ
−⋅⋅π
=
С
СП
r
R
n
PPk2
Q
l
, (8)
где через <k> обозначено среднее по всем направлениям θ значение проницае-
мости рассматриваемой анизотропной среды, т.е.
()
∫
π
θ⋅θ⋅⋅
π
=
2
0
dcosfk
2
1
k
. (9)
Решение (8) от классической формулы Дюпюи [7, 24, 103, 258] отличается
только тем, что вместо проницаемости изотропного пласта появилось среднее
значение проницаемости <k>.
Рассмотрим теперь другое течение типа точечного вихря, расположенного
в начале координат. В этом течении v
x
= -v⋅sin(θ), поэтому
()
θ−=
sinf
v
v
f
x
. По-
скольку сейчас v
r
= 0, то из (6) вытекает, что ϕ = ϕ(θ), а ψ = ψ(r). Теперь из сис-
темы (6) находим следующее частное решение:
()
()
DrnA;C
sinf
d
A +⋅−=ψ+
θ−
θ
⋅=ϕ
∫
l , (10)
где A, C, D - произвольные постоянные, которые можно определить, если будет
задана конкретная область течения и граничные условия. Пусть, к примеру, об-
ласть течения – четверть кругового кольца, ограниченная осями x, y и окружно-
стями r = r
1
, r = r
2
(где r
1
< r
2
, 0 ≤ θ ≤ π/2). В этом течении величина потока П от
отрезка r
1
≤ x ≤ r
2
на оси x-ов к отрезку r
1
≤ y ≤ r
2
на оси y-ов равна
⋅=⋅=
∫
θ
1
2
r
r
r
r
nAdrvП
2
1
l . Если на границах осей x и y будут заданы значения
C
yось
П
xось
и ϕ=ϕϕ=ϕ , то A можно вычислить из этих граничных условий. В
результате для такого потока П получим значение
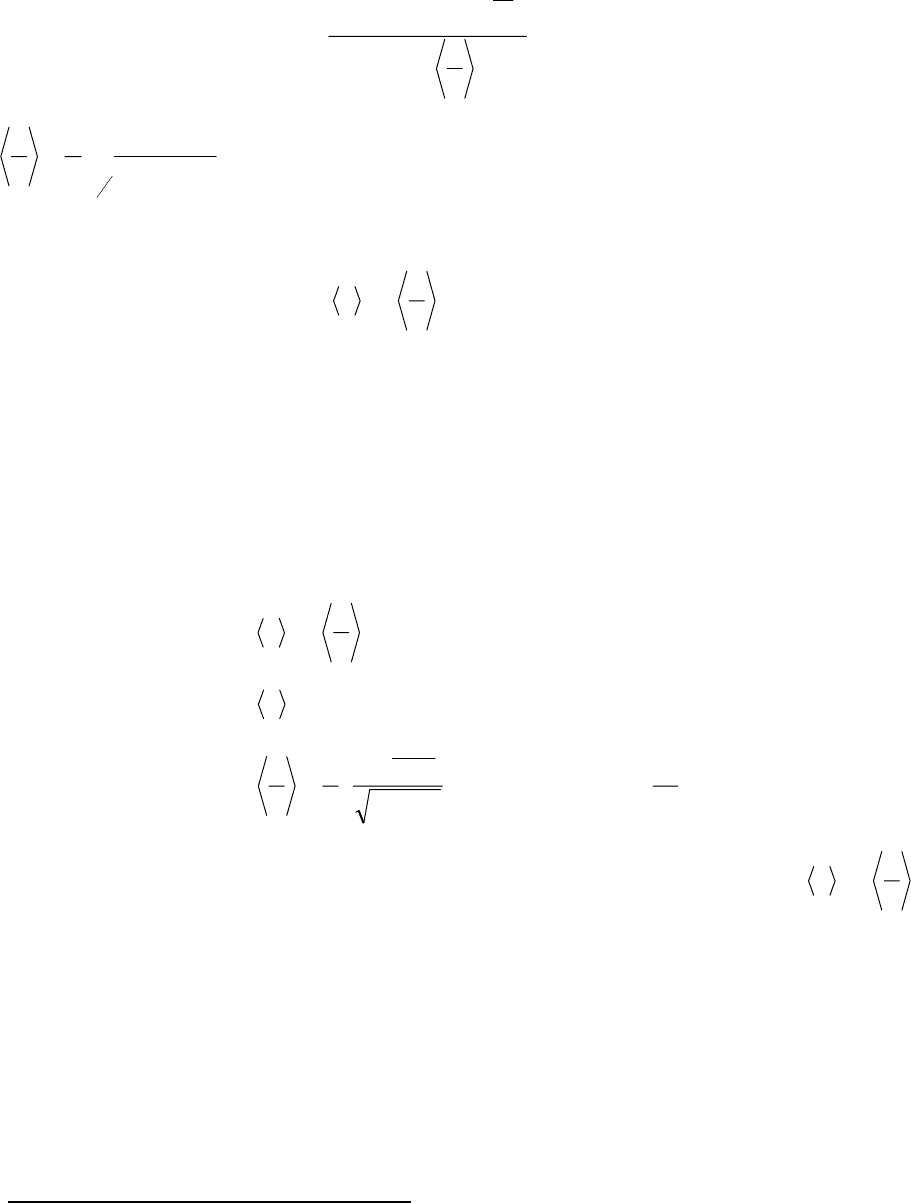
60
()
k
1
r
r
nPP2
П
1
2
СП
⋅µ⋅π
⋅−⋅
=
l
, (11)
где
()
∫
π
π
θ⋅
θ
⋅
π
=
2
cosfk
d2
k
1
. Формулы (8) и (11) имеют важное практическое значе-
ние, т.к. с их помощью по результатам лабораторных испытаний можно было
бы измерить средние значения
k и
k
1
. Затем по измеренным средним можно
найти параметры функции f(cosθ), которая аппроксимирует зависимость про-
ницаемости среды от направления вектора
v
r
. Например, если ось x-ов обладает
асимметрией и проницаемость, как функция направления вектора скорости
фильтрации, аппроксимируется зависимостью вида
f(cos θ) = a
0
+ a
1
⋅cos θ , где 0 < a
1
< a
0
, (12)
то для средних значений
k и
k
1
найдём выражения:
=α
−
π
α⋅
+
⋅=
⋅=
0
1
2
1
2
0
0
a
a
arcsinгде,
aa
2
1
k
1
k
1
akk
. (13)
Теперь из системы уравнений (13) по измеренным величинам средних
k и
k
1
можно найти параметры a
0
и a
1
в формуле (12).
Таким образом, обобщённый метод С.Н. Нумерова позволяет в рассмот-
ренном случае предложить, с привлечением экспериментальных данных, мате-
матическую модель плоскопараллельной нелинейной фильтрации в анизотроп-
ной среде с весьма необычными свойствами.
Основные результаты 1-й главы:
1) выведены формулы для расчёта глав-
ных проницаемостей по методам локального и интегрального однородно-
анизотропного эквивалентирований периодических сред специального класса,
2) развит метод расчёта тензоров проницаемостей анизотропных моделей пе-
риодических сред по заданным полям ГНА и главных проницаемостей как для
