Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.


230
от отношения проницаемостей
0
1
k
k
ПЗС и остального пласта. В эксперименте ради-
ус контура питания R = 10 км, радиус ПЗС R
0
= 10 м., радиус скважин r
C
= 0,1 м. На
рисунках 63-65 приведены графики зависимости суммарного относительного де-
бита батареи скважин от n и
0
1
k
k
.
Вычислительный эксперимент показал, что повышение проницаемости
ПЗС более чем в 20 раз неоправданно. В промысловой практике достаточно
увеличивать проницаемость ПЗС в 5 раз, т.к. дальнейшее увеличение прони-
цаемости уже не столь эффективно.
Кроме того, результаты вычислительных экспериментов, представленные
графически на рисунках 63-65, показали, что ухудшение проницаемости ПЗС
сильнее сказывается на суммарном дебите батареи скважин, чем её увеличение.
Поэтому при эксплуатации скважин необходимо предусматривать меры, пре-
дотвращающие понижение проницаемости ПЗС с течением времени.
5.6. Интерференция скважин с нелинейным режимом фильтрации в приза-
бойных зонах
Особые фильтрационные свойства пласта в ПЗС могут появляться и без
специальных воздействий на околоскважинные области. Это связано с тем, что
с увеличением дебитов скважин скорости течения в ПЗС могут вырасти на-
столько, что в околоскважинной области фильтрация будет подчиняться уже
нелинейному закону Дарси [112]
v
v
)v(fPgrad ⋅−= , (1)
где P - приведённое давление, а f(v) – функция, определяемая эксперименталь-
но и характеризующая конкретный закон фильтрации. На практике чаще всего,
кроме линейного закона, распространены квадратичный закон фильтрации и
степенные законы, в частности закон А.А. Краснопольского [112]. Чем больше
дебит, тем больше размеры ПЗС, внутри которой фильтрация будет подчинять-
ся нелинейному закону Дарси. Понятно поэтому, что теория взаимодействия n

231
скважин, в призабойных зонах которых может нарушаться линейный режим
фильтрации, является актуальной для нефтепромысловой практики.
Для исследования влияния призабойных зон с нелинейной фильтрацией
(ПЗНФ) на дебиты скважин
предлагается следующая модель:
1). ПЗНФ для каждой скважины γ
m
с радиусом r
0m
(m = 1,2,…,n) и с цен-
тром в точке (x
m
,y
m
) снова моделируем как круговую с границей (5.1) и с радиу-
сом r
m
. Подчеркнём, что радиусы ПЗНФ теперь считаются заранее не извест-
ными и подлежащими определению.
2). Будем предполагать, что радиусы r
m
ПЗНФ малы по сравнению с рас-
стояниями между скважинами и другими характерными размерами области те-
чения. Поэтому течение жидкости в ПЗНФ будем рассматривать как одномер-
ное радиальное. Вследствие последнего удельный дебит
mm
2Q λ⋅π= скважины
γ
m
будем рассчитывать по формуле Дюпюи для нелинейного режима фильтра-
ции, имеющей вид [112]:
m
r
r
*
m
m
m
PPdr
r
f
m
m0
−=⋅
λ
∫
, (2)
где f
m
– функция f
m
(v), характеризующая конкретный вид закона Дарси в ПЗС
γ
m
, а остальные обозначения прежние.
3). Фильтрация за пределами каждой ПЗНФ описывается уравнением (1.2),
а удельные притоки Q
m
к границам C
m
можно вычислить по методу §5.5.
Если условия 1), 2) и 3) окажутся выполненными, то для расчёта удельных
дебитов скважин, обладающих ПЗНФ, можно воспользоваться системой урав-
нений (5.3), в которой, однако, второе уравнение надо будет заменить на (2).
Кроме того, сейчас появились как неизвестные радиусы r
m
границ ПЗНФ. Эти
радиусы предлагается определять по значению критического числа Рейнольдса
[112] на границе C
m
:
()
σε⋅
ν
⋅
= ,C,f
kv
Re
1кр
, (3)
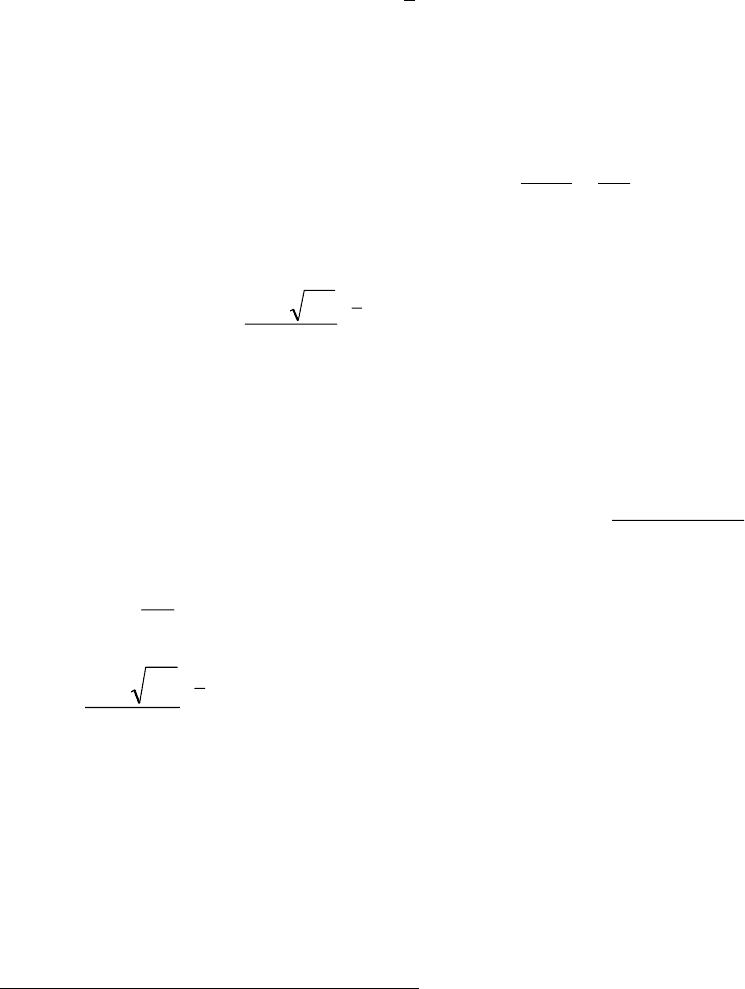
232
где v – скорость фильтрации, k - проницаемость среды, ν = µ/ρ - коэффициент
кинематической вязкости жидкости,
(
)
σε ,C,f
1
- некоторая безразмерная функ-
ция, вид которой определяется опытным путём, ε и C
1
– параметры шерохова-
тости и извилистости поровых каналов среды, σ - коэффициент пористости
среды. Поскольку на границе С
m
скорость
m
m
m
m
rr2
Q
v
λ
=
π
= , то уравнение для r
m
,
как следует из (3), будет иметь вид
()
крmm1m
m
mm
Re,C,f
r
k
=σε⋅
⋅ν
⋅λ
. (4)
Таким образом, окончательно для расчёта дебитов скважин γ
m
, обладающих
ПЗНФ, получаем следующую систему нелинейных алгебраических уравнений
() ( )
()
()
≠=
=σε⋅
⋅ν
⋅λ
−=⋅
λ
µ
−⋅
=∆+∆+ϕ⋅λ+ϕ⋅λ
∫
∑
=
mi;n,...,2,1m
Re,C,f
r
k
PPdr
r
f
PPk
yy,xxy,x'
крmm1m
m
mm
m
r
r
*
m
m
m
*
mП0
mmmmmm
n
1i
mmii
m
m0
. (5)
Система (5) из 3n уравнений замкнутая, так как число неизвестных λ
1
, λ
2
, ….,λ
n
,
P
*
1
, P
*
2
, … ,P
*
n
, r
1
, r
2
, …, r
n
, соответствует числу уравнений. Решив систему (5), оп-
ределим и удельные дебиты и поле давлений, т.е. получим полное решение задачи.
Основные результаты 5-ой главы:
1) разработаны общие математические
модели, описывающие работу в изотропном неоднородном пласте
а) одиночной
скважины, б) группы скважин, в) группы скважин со скачками проницаемо-
стей в ПЗС, г) группы скважин с нелинейным режимом фильтрации в ПЗС
; 2)
предложен метод построения серии точных решений (в постановке для двух-
связных областей) задач фильтрации к круговой скважине с конечным радиу-
сом; 3) предложены вариационные методы расчёта верхних и нижних оценок
дебита одиночной скважины; 4) по предложенным математическим моделям
выполнены вычислительные эксперименты и сделаны выводы.

233
ГЛАВА 6. ТЕОРИЯ РАСЧЕТОВ ФИЛЬТРАЦИОННЫХ ТЕЧЕНИЙ В
МНОГОСЛОЙНЫХ И НЕОДНОРОДНЫХ СРЕДАХ В ПРЯМОУГОЛЬНОЙ
ОБЛАСТИ
В 6-й главе разрабатывается теория расчётов плоскопараллельных
фильтрационных течений в многослойной области G в виде криволинейного
четырехугольника, ограниченного дугами координатных линий
ортогональной изотермической системы координат P, Q. Расчётная область
заполнена многослойной неоднородной анизотропной средой (МС-средой),
границы отдельных слоёв которой совпадают с линиями P = const (или Q =
const). В изотермических P, Q и в декартовых (для прямоугольной области)
координатах x, y расчёт поля в МС-среде осуществляется по алгоритмам,
которые отличаются лишь непринципиальными деталями. Поэтому без
ограничения общности рассматривается область G = {0≤ x ≤ l; 0 ≤ y ≤ h} в
виде прямоугольника MBED (рис.66), заполненного средой с прямолинейной
анизотропией.
6.1. Постановка задачи и принятые обозначения
Пусть требуется рассчитать некоторое векторное поле
j)y,x(i)y,x()y,x(
yx
r
r
r
υ+⋅υ=υ в прямоугольной области G = {0≤ x ≤ l; 0 ≤ y ≤ h}
границы у = 0 и у = h которой назовём прямыми MD и BE соответственно.
Область G считается заполненной материальной средой с прямолинейным
типом анизотропии и физические характеристики которой претерпевают
конечные разрывы во внутренних точках 0 = х
0
< х
1
< х
2
< х
3
< ... < х
n-1
< x
n
= l
области G. Такая ситуация типична, например, для кусочно-однородных сред в
теории фильтрации. Главные направления анизотропии (ГНА) в каждой точке
пусть совпадают с осями х и у декартовой системы координат, а собственные
значения Г
1
(х) и Г
2
(х) тензора проницаемости, описывающие физические
свойства среды, на каждом из отрезков ∆
i
= [x
i-1
, x
i
] равны
,n,...,1i),x(f
~
Г);x(f
~
Г
iiii2
х
2iii1
х
1
ii
=⋅γ⋅ε=γ=⋅γ=γ=
∆∈∆∈
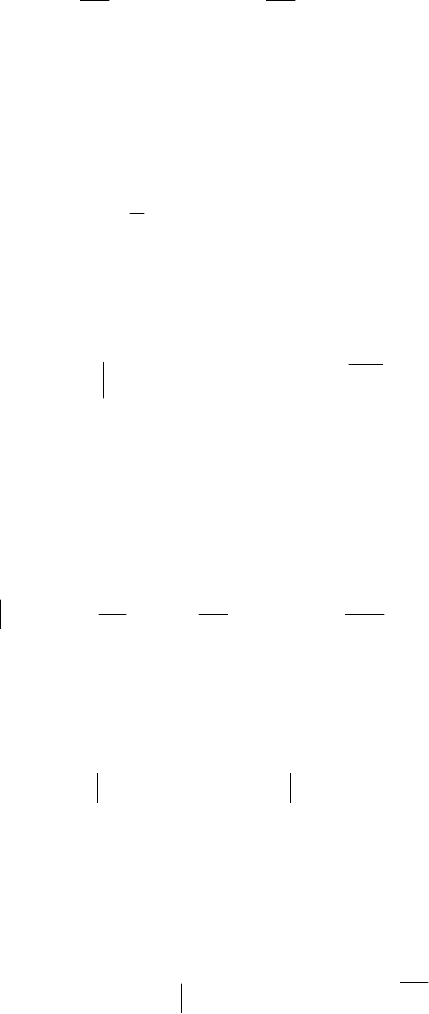
23
4
где f
i
(x) - непрерывная положительная на указанном отрезке функция
принимающая н его концах значения
(
)
1
1
=
−ii
xf ,
(
)
iii
xf
τ
= ,
i
ε
,
i
γ
,
i
τ
—
положительные постоянные (рис.66). Коэффициент
i1i2
~
/
~
γ
γ
=
ε
,будем называть
коэффициентом анизотропии i-го слоя [x
i-1
, x
i
], а τ
i
– коэффициентом
неоднородности i-го слоя. Безразмерные уравнения, описывающие поле
)у,х(
υ
r
в
рассматриваемой кусочно неоднородной среде с прямолинейной анизотропией,
имеют вид
,
у
Г,
х
Г
2у1х
∂
ϕ
∂
⋅−=υ
∂
ϕ
∂
⋅−=υ (1)
где ϕ (х, у) – некоторая скалярная функция, называемая потенциалом поля.
Кроме уравнения (1), поле
)у,х(
υ
r
должно удовлетворять уравнению
неразрывности, имеющему вид
)у(div Ω−=υ
)
(2)
в котором
()
yΩ
)
- плотность источников, определяемая для каждого i-го слоя
через заданные кусочно-непрерывные по у функции ω
i
(y) формулой
.n,1i),у()у(
ii
]х,х[х
i1i
=ω⋅γ=Ω
−
∈
)
(3)
После подстановки (1) в (2) для искомого потенциала поля ϕ = ϕ (х,у) получаем
следующее уравнение эллиптического типа с кусочно-непрерывными
коэффициентами
[]
)у(
у
)х(F
х
)х(F
х
)х(F,)у,х(L
2
2
Ω=
∂
ϕ∂
⋅⋅ε+
∂
ϕ∂
⋅
∂
∂
≡εϕ
))
(4)
В уравнении (4) через
)х(F,ε
)
и Ω(у) обозначены следующие кусочно-
непрерывные функции, задаваемые на i-ом слое формулами
).у()у();х(f)х(F,|
i
х
i
х
iх
iii
i
ω=Ω=ε=ε
∆∈∆∈
∆∈
)
Если значение потенциала ϕ(х, у) послойно перенумеровать, то одно уравнение
(4) с кусочно-непрерывными коэффициентами будет эквивалентно следующей
системе уравнений эллиптического типа
[
]
.n,1i);у()х(f,)у,х(L
iiii
=ω=εϕ (5)

235
Однако в данной работе на систему уравнений (5) мы смотрим не только как на
развёрнутую запись одного уравнения (4). Кроме такой точки зрения на систему
(5), в работе будут рассматриваться и две другие. Первая – если имеется готовый
алгоритм решения системы уравнений (5) (пусть даже для некоторого
ограниченного класса функций f
i
(x) ), то насколько точно решение уравнения
(4) с непрерывной в G, но сложной для интегрирования функцией F(x) и
постоянной
ε
)
, можно свести к решению системы (5), совокупность простых
функций f
i
(x) которой будет в некотором смысле эквивалентна F(x). Вторая –
насколько точно расчёт поля в кусочно-непрерывных средах с
характеристиками ε
i
и f
i
(x), требующий решения системы уравнений (5), можно
заменить на расчёт поля в сплошной непрерывной среде с эквивалентными в
некотором смысле характеристиками
ε
)
и F(x), требующий решения только
одного уравнения (4). Заметим, что в электротехнике при исследовании полей в
многослойных средах второй из подходов часто, начиная с 1925 г., применялся
Оллендорфом и предложенная им методика анизотропного эквивалентировая
широко внедрилась в практику расчётов несмотря на то, что анализ
погрешности метода и до настоящего времени изучен не достаточно.
6.2. Граничные условия 1-го типа (Дирихле по одной паре
противоположных сторон прямоугольника и смешанные — по другой паре)
Перечислим теперь граничные условия, совместно с которыми решается
система уравнений (1.5). Во –первых, на сторонах ВЕ и MD
задаются условия
Дирихле:
.n,1i);х(Ф)h,х();х(Ф)0,х(
2
х
i1
х
i
iiii
==ϕ=ϕ
∆∈∆∈
∆
(1)
где Ф
1
(х) и Ф
2
(х) – заданные непрерывные на [0, l] функции. На сторонах МВ
и DE могут быть заданы различные условия – либо закон распределения
потенциала (условия Дирихле), либо закон распределения нормальной
составляющей v
n
. Чтобы одновременно рассмотреть каждый из этих случаев,
запишем граничные условия на сторонах МВ и DE в виде:

236
)у(F
х
bа);у(F
х
bа
2
lх
n
*
2n
*
21
0х
*
11
*
1
=
∂
ϕ∂
+ϕ⋅=
∂
ϕ∂
⋅+ϕ⋅
==
. (2)
Если в (2) положить
,1аа,0bb
*
2
*
1
*
2
*
1
==== то получим случай заданного с
помощью функций F
1
(y) и F
2
(y) на границах х = 0 и х = l закона
распределения потенциала. Если же взять
nn
*
21
*
1
*
2
*
1
b,bи0аа γτ=γ−=== , то
получим случай заданного на границах МВ и DE закона распределения
нормальной составляющей v
n
.
На границах контактов слоёв
друг с другом должны выполняться
условия непрерывности потенциала и нормальных составляющих v
n
, т.е.
при х = х
i-1
: ϕ
i-1
= ϕ
i
и .n,2i,
хх
i
i
1i
1i1i
=
∂
ϕ∂
⋅γ=
∂
ϕ
∂
⋅τ⋅γ
−
−−
(3)
6.3. Передаточные функции. Переход к модельной задаче
Для дальнейшего понадобятся специальные частные решения
однородного уравнения (1.5)
[
]
0)х(f,)у,х(L
iii
=εψ (1)
в областях g
i
= {x
i-1
< x < x
i
; 0 < y < h}, которые на границах у = 0 и у = h
удовлетворяют некоторым непрерывным условиям типа Дирихле, а в
вершинах g
i
принимают заданные значения )n,1i( =
.)h,х(;)0,х(;)h,х(;)0,х(
iEiiiDiiiB1iiiM1ii
ϕ=
ψ
ϕ
=
ψ
ϕ
=
ψ
ϕ=ψ
−−
(2)
Непосредственной проверкой можно убедиться, что такими решениями
уравнения (1), удовлетворяющими заданным значениям в вершинах
прямоугольной области g
i
, являются функции
∫
∫
∫
∫
−
−
−
−
⋅
⋅+
⋅+⋅+=ψ
i
1i
1i
i
1i
1i
х
х
i
х
х
i
ii
х
х
i
х
х
i
iii
)х(f
dx
)х(f
dx
h
у
d
~
h
у
с
~
)х(f
dx
)х(f
dx
b
~
а
~
)у,х(
(3)
коэффициенты в которых равны:
.d
~
,с
~
,b
~
,а
~
iDiBiMiEiiMiBiiMiDiiMi
ϕ−ϕ−ϕ+ϕ=ϕ−ϕ=ϕ−ϕ=ϕ= (4)

237
Функции ψ
i
(х,у) будем называть передаточными функциями. Из (3) вытекает,
что ψ
i
(х,у) на сторонах х = х
i-1
и х = х
i
области g
i
изменяется по линейному
закону, а на сторонах у = 0 и у = h изменяется непрерывно от ϕ
iM
до ϕ
iD
и от
ϕ
iВ
до ϕ
iЕ
соответственно - см. рис.67. Если заданные значения ψ
i
(х,у) в
вершинах области g
i
определить с помощью условий (2.1) по формулам
ϕ
iM
= Ф
1
(х
i-1
); ϕ
iB
= Ф
2
(х
i-1
); ϕ
iD
= Ф
1
(х
i
); ϕ
iЕ
= Ф
2
(х
i
), (5)
то функции ψ
i
(х,у) на границах у = 0 и y = h в точках х
i
, i = n,0 , будут
принимать значения, совпадающие соответственно со значениями граничных
условий Ф
1
(х) и Ф
2
(х). Далее первоначально заданные граничные условия
(2.1) будем заменять на новые приближённые к ним граничные условия
)h,х()h,х();0,х()0,х(
i
х
ii
х
i
ii
ψ=ϕψ=ϕ
∆∈∆∈
, (6)
в которых коэффициенты функций ψ
i
(х,у) вычисляются по формулам (4) и
(5). Ели длины частичных отрезков ∆
i
= [x
i-1
, x
i
] малы, то функции ψ
i
(х,у)
достаточно точно передадут (откуда и происходит их название) значения
заданных граничных условий. Если же отрезки ∆
i
будут велики, то их можно
разбить на более мелкие составные части, добавив ряд новых точек деления.
Постановка задачи и её решение от этого принципиально не меняется. К тому
же из общей теории линейных уравнений эллиптического типа, к которым
относится уравнение (1.4), известно, что краевые задачи Дирихле являются
корректными. Поэтому решение уравнения (1.4) с условиями (2.1) будет мало
отличаться от решения этого же уравнения, но с приближёнными
граничными условиями (6). Количественную оценку в изменении решения
при замене точных граничных условий на приближённые будем определять с
помощью вычислительных экспериментов. Краевую задачу для уравнения
(1.4) с новыми граничными условиями (6) будем называть модельной
задачей.

238
6.4. Формулировка граничных условий в модельной задаче
Решение уравнений (1.5) будем представлять в виде сумм
ϕ
i
(x,y) = ψ
i
(x,y) +w
i
(x,y), (1)
в которых ψ
i
(x,y) – передаточные функции (3.3). После подстановки (1) в
(1.5) и учитывая, что ψ
i
(x,y) удовлетворяют однородному уравнению (3.1),
для функций w
i
(x,y) получим уравнения
.n,1i);у()]х(f,)у,х(w[L
iiii
=ω=ε (2)
Так как в модельной задаче при у = 0 и у = h выполняются условия (3.6), то
на сторонах MD и BE
функции w
i
(x,y) должны будут удовлетворять
однородным граничным условиям
w
i
(x,0) = w
i
(x,h) = 0. (3)
На границах контакта
слоёв g
i
друг с другом должны выполняться условия
(2.3). Подставляя в (2.3) выражения (1) и учитывая формулы (3.3) и (3.4),
граничные условия сопряжения в модельной задаче после преобразований
примут вид: при х = х
i-1
n,2i);у,х(w)у,х(w
1ii1i1i
==
−−−
(4)
и
).у(L
х
w
х
w
1i
i
i
1i
1i1i −
−
−−
+
∂
∂
⋅γ=
∂
∂
⋅τ⋅γ (5)
В формуле (5) через L
i-1
(y) обозначена функция
() ()
∆Φ−∆Φ⋅+∆Φ
⋅γ−
∆Φ−∆Φ⋅+∆Φ
γ=
∫∫
−
−−
−
−−−
−−
1i
2i
i
1i
х
х
1i
)1i(
1
)1i(
2
)1i(
1
1i
х
х
i
)i(
1
)i(
2
)i(
1
i1i
)х(f
dx
h
у
)х(f
dx
h
у
)у(L
в которой
)1i(
1
−
∆Φ и
)i(
2
∆Φ - приращения функций Ф
1
(х) и Ф
2
(х) на отрезках ∆
i-1
и ∆
i
:
)х(Ф)х(Фи)х(Ф)х(
1i2i2
)i(
21i1i1
)i(
1 −−
−=∆Φ−Φ=∆Φ (6)
На сторонах MВ и DE,
т.е. при х = 0 и х = l, должны выполняться условия
(2.2). Подставляя в (2.2) функции
111
w
+
=
ψ
ϕ
и
nnn
w+=
ψ
ϕ
, после

239
преобразований для соответствующих граничных условий в модельной
задаче получим:
)y(F
x
w
bwa
1
0x
1
111
)
=
∂
∂
⋅+⋅
=
∗∗
, (7)
)y(F
x
w
bwa
2
lx
n
2n2
)
=
∂
∂
⋅+⋅
=
∗∗
, (8)
где через
()
yF
1
)
и
()
yF
2
)
обозначены выражения
[]
()
∫
∆Φ−∆Φ+∆Φ
−
Φ−Φ+Φ−=
∗∗
1
x
0
1
)1(
1
)1(
2
)1(
1
1121111
)x(f
dx
h
y
b)0()0(
h
y
)0(a)y(F)y(F
)
(9)
и
[]
(
)
∫
−
τ
∆Φ−∆Φ+∆Φ
−
Φ−Φ+Φ−=
∗∗
n
1n
x
x
n
n
)n(
1
)n(
2
)n(
1
2121222
)x(f
dx
h
y
b)l()l(
h
y
)l(a)y(F)y(F
)
(10)
Итак, задача о расчёте поля в многослойной среде (MC-среде) свелась к
решению системы уравнений (2) с граничными условиями (3)-(5),(7) и (8).
6.5. Представление решений w
i
(x, y) рядами Фурье
Решения системы уравнений (4.2) в модельной задаче будем представлять в
виде тригонометрических рядов Фурье
∑
∞
=
λ⋅=
1k
kiki
)ysin()x(U)y,x(w , где
h
k
k
π
=λ
. (1)
Такая форма представления
)y,x(w
i
выбрана потому, что граничные условия
(4.3) благодаря ей оказываются выполненными. Функции же U
ik
(x) в (1)
подберём так, чтобы при подстановке w
i
(x,y) в уравнение (4.2) последнее
обратилось в тождество. Предполагая правомочность двукратного
дифференцирования рядов (1) по каждому аргументу, после подстановки (1) в
(4.2) получим:
∑
∞
=
ω=λ⋅
⋅⋅ε⋅λ−
⋅
1k
).y()ysin()x(U)x(f
dx
)x(dU
)x(f
dx
d
ikikii
2
k
ik
i
(2)
