Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.

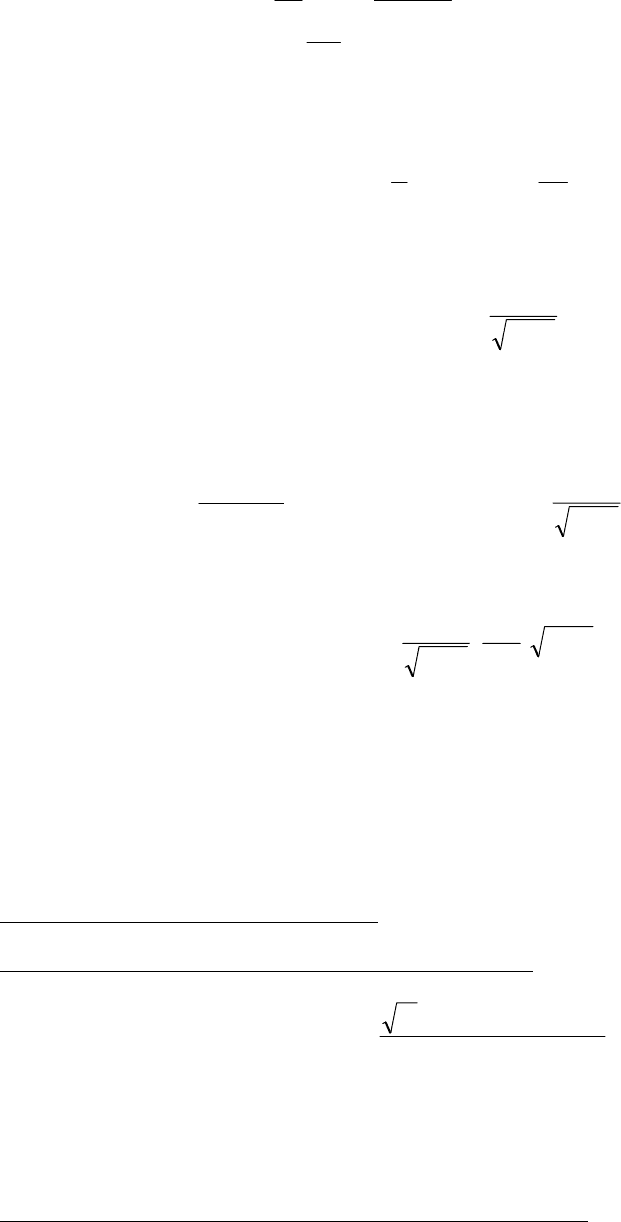
240
Если теперь разложить ω
i
(у) в ряд Фурье по синусам sin(λ
k
⋅y) и затем сравнить
левые и правые части (2), то для функций U
ik
(x) получим следующие
дифференциальные уравнения:
∞==
=⋅⋅ε⋅λ−
⋅
,...,3,2,1k;n,1i
,A)x(U)x(f
dx
)x(dU
)x(f
dx
d
ikikii
2
k
ik
i
(3)
где А
ik
– коэффициенты Фурье для функций ω
i
(у), т.е.
.dyy
h
k
sin)y(
h
2
A
h
0
iik
∫
π
⋅ω⋅=
(4)
Решения уравнений (3) будем искать с помощью подстановки
.
)x(f
)x(V
)x(U
i
ik
ki
=
(5)
Выполнив преобразования, для вспомогательной функции V
ik
(x) получим
уравнение:
[]
,
)x(f
A
)x(V)x(H
dx
)x(Vd
i
ik
ikii
2
k
2
ik
2
=⋅+ε⋅λ− (6)
в котором через H
i
(x) обозначено выражение
(
)
.)x(f
dx
d
)x(f
1
)x(H
i
2
2
i
i
⋅= . (7)
Формулы (5), (6) и (7) показывают, что вид функций U
ik
(x) зависит от закона
изменения неоднородности i-го слоя g
i
. Поэтому выделим прежде всего те
частные случаи законов изменения f
i
(x), когда уравнение (6) имеет постоянные
коэффициенты. Таких случаев три.
1). Однородно - анизотропная среда
f
i
(x) = 1; (τ
i
= 1). (8)
2). Анизотропная среда с квадратичным законом
изменения неоднородности:
()()
.
xx
xxxx
)x(f
2
1ii
i1ii
i
−
−+−⋅τ
=
−
−
(9)
Подчеркнём, что если τ
i
= 1, то из (9) будет вытекать важный частный случай
однородно - анизотропной среды (8).
3). Анизотропная среда с экспоненциальным законом.

241
τ⋅
−
−
=
−
−
i
1ii
1i
i
ln
xx
xx
exp)x(f
. (10)
Здесь тоже при τ
i
= 1 получим 1-ый случай (8).
Из всех перечисленных наиболее приемлемым с точки зрения
универсальности получаемых вычислительных алгоритмов, предназначенных
для вычисления полей в широком спектре многослойных и неоднородных сред,
оказывается последний третий случай. Именно поэтому в дальнейшем под
функцией f
i
(х) (если нет специальных оговорок) будет пониматься функция
(10), или, если τ
i
= 1, то считается что f
i
(х) ≡ 1. Решая известными методами
уравнение (6), в котором f
i
(х) задана по формуле (10), для функций U
ik
(x)
получим выражения
,
)x(f
A
)x(pD)x(gC)x(U
ii
2
k
ik
ikikikikik
⋅ε⋅λ
−⋅+⋅=
(11)
где g
ik
(x) и p
ik
(x) – линейно независимые частные решения однородного
уравнения, соответствующего уравнению (3). Эти частные решения удобно
подобрать так, чтобы они удовлетворяли следующим краевым условиям:
g
ik
(x
i-1
) = 1; g
ik
(x
i
) = 0; p
ik
(x
i-1
) = 0; p
ik
(x
i
) = 1. (12)
Такие решения, как легко проверить, имеют вид:
[
]
()
[
]
()
,
dsh)x(f
)xx(sh
)x(p;
dsh)x(f
)xx(sh
)x(g
iiki
1iiki
ik
iiki
iik
ki
⋅β⋅
−⋅β⋅τ
=
⋅β⋅
−⋅β
=
−
(13)
в котором обозначено
.
d2
ln
a;a;xxd
i
i
i
2
ii
2
kik1iii
τ
=+ε⋅λ=β−=
−
(14)
Подчеркнём, что если в формулах (11) и (13) положим f
i
(х) ≡1 и τ
i
= 1, то
получим, как частный случай, решение относящееся к однородному закону (8).
6.6. Алгебраизация граничных условий в модельной задаче
Рассмотрим теперь граничные условия (4.4), (4.5), (4.7) и (4.8). Подставляя
в (4.4) выражения (5.1) и учитывая равенства (5.12), получим систему уравнений

242
∞==
ε⋅λ
−=
τ⋅ε⋅λ
−
−−
−
−
),1k;n,2i(
A
С
A
D
i
2
k
ik
ik
1i1i
2
k
k,1i
k,1i
. (1)
Аналогично, подставляя в (4.5) выражения (5.1) и выполняя необходимые
преобразования, приходим к системе уравнений
=
ε⋅λ
⋅⋅
γ
⋅
+⋅−⋅τ⋅γ+⋅α⋅γ−
−
−−−
−−−−−−−
1i
2
k
k,1i1i1i
k,1i1ik,1i1i1iikk,1i1i
Aa2
D)ar(C
),1k;n,2i(
;L
Aa2
DC)ar(
k,1i
i
2
k
ikii
ikikiikiiki
∞==
+
ε⋅λ
⋅
γ
⋅
+⋅α⋅γ+⋅+⋅γ−=
−
(2)
В системе уравнений (2) через α
ik
и r
ik
обозначены выражения:
()
()
iikikik
iik
iik
ik
dcthr;
dsh
⋅β⋅β=
⋅β
τ⋅β
=α (3)
а через L
i-1,k
– коэффициенты разложений в ряды Фурье функций L
i-1
(у).
Последние имеют вид:
(
)
(
)
[
]
{
+∆Φ−∆Φ−∆Φ−∆Φ⋅−⋅
π
=
−−
−
+
−
)1i(
1
)1i(
21i
)i(
1
)i(
2i
1k
k,1i
TT)1(
k
2
L
[
]
(
)
}
)1i(
11i
)i(
1i
k
TT)1(1
−
−
∆Φ⋅−∆Φ⋅⋅−−+ , (4)
где через T
i
обозначены выражения
=τ
γ
≠τ
⋅−τ
τ⋅τγ
=
1если,
d
1если,
d)1(
)ln(
T
i
i
i
i
ii
iii
i
(5)
Наконец, подставляя w
1
(x,y) и w
n
(x,y) из (5.1) в (4.7) и (4.8) соответственно, для
граничных условий при х = 0 и х= l получим выражения:
[]
(
)
1
2
k
k1111
k1k11k11k111k1
Aba2a
FbD)ar(baC
ε⋅λ
⋅−
+=α⋅⋅++⋅−⋅
∗∗
∗∗∗
)
(6)
и
[]
(
)
nn
2
k
nk2n2
k2nknnk22
n
nknk2
Aba2a
FD)ar(ba
Cb
τ⋅ε⋅λ
⋅−
+=−++
τ
⋅α⋅
−
∗∗
∗∗
∗
)
. (7)
Через
k1
F
)
и
k2
F
)
в (6) и (7) обозначены коэффициенты разложений в ряды Фурье
функций
()
yF
1
)
и
()
yF
2
)
, т.е.

243
dy)ysin()y(F
h
2
F;dy)ysin()y(F
h
2
F
k
h
0
2k2k
h
0
1k1
⋅λ⋅⋅=⋅λ⋅⋅=
∫∫
))))
Таким образом, для отыскания потенциалов поля необходимо решить
систему линейных алгебраических уравнений (1), (2), (6) и (7).
6.7. Вычисление коэффициентов в рядах Фурье методом прогонки
Уравнение (6.1) показывает, что коэффициенты
k,1i
D
−
выражаются через
ik
C . В частности,
k1
D будет вычисляться через
k2
C . Подставляя
k1
D , выраженный
из (6.1) через
k2
C , в уравнение (6.6), получаем связь между коэффициентами
k1
C
и
k2
C . Эта связь, после преобразований, даёт следующее уравнение:
k2k2k2k1
SCmC
+
⋅
=
, (1)
где
)ar(ba
ab
m
1k111
k11
k2
+⋅−
⋅
−=
∗∗
∗
(2)
и
ελ
−
τελ
−
ελ
−
+
+−
=
∗
∗∗
∗∗
2
2
k
k2
11
2
k
k1
k11
1
2
k
k1111
k1
1k111
k2
AA
ab
A)ba2a(
F
)ar(ba
1
S
)
(3)
Аналогично, вычисляя с помощью уравнений (6.1)
k,1i
D
−
через
ik
C и
ik
D
через
k,1i
C
+
и подставляя затем эти выражения в (6.2), относительно
коэффициентов
k,1i
C
−
,
k,i
C и
k,1i
C
+
получим трёхдиагональную систему линейных
алгебраических уравнений. Такие системы, как известно, решаются методами
прогонки. В соответствии с алгоритмом названного метода связь между
коэффициентами
ik
C и
k,1i
C
+
ищем в линейной форме
k,1ik,1ik,1iik
SCmC
+++
+
⋅
=
, (4)
в которой
k,1i
m
+
и
k,1i
S
+
- пока неизвестные прогоночные коэффициенты. Для
определения прогоночных коэффициентов подставим
ikikikk,1i
SCmC
+
⋅
=
−
(5)

24
4
в трёхдиагональную систему линейных относительно
ikk,1i
C,C
−
и С
i+1,k
алгебраических уравнений. В результате подстановки и последующих
преобразований получим рекуррентные формулы:
()
()
ikk,1i1iiiki1ik,1i1i1i
iki
k,1i
marar
m
⋅α⋅γ−+⋅γ+−⋅τ⋅γ
α
⋅
γ
=
−−−−−−
+
(6)
и
()
α⋅γ
+
ε⋅λ⋅α⋅γ
⋅⋅γ
−
ε⋅α⋅λ
⋅
+
+
ε⋅λ
−
τ⋅ε⋅λ
⋅−⋅
α⋅γ
τ⋅γ
−
−
ε⋅λ
−
τ⋅ε⋅λ
+
α⋅γ
⋅α⋅γ
⋅=
−
−
−−−
−−
−
−−
−−
+
+−−
++
iki
k,1i
1i
2
kiki
k,1i1i1i
iik
2
k
iki
i
2
k
ik
1i1i
2
k
k,1i
1ik,1i
iki
1i1i
1i
2
k
k,1i
ii
2
k
ik
iki
ikk,1i1i
k,1ik,1i
LAa2
Aa2
A
A
ar
A
A
S
mS
(7)
Отправляясь от известных значений m
2k
и S
2k
в (2) и (3), по рекуррентным
формулам (6) и (7) вычислим m
3k
,…, m
nk
и S
3k
, …, S
nk
(т.к. i = 2,3,…,(n - 1)).
Рассмотрим теперь уравнения (6.1), (6.2) и (6.7) при i = n. Из (6.1)
k,1n
D
−
выразим через
nk
C и подставим в (6.2). Коэффициент
k,1n
C
−
по формуле (5)
выразим через
nk
C и тоже подставим в (6.2). Тогда, преобразованное таким
способом уравнение (6.2) и уравнение (6.7) дадут систему двух уравнений
относительно неизвестных
nk
C и
nk
D . Решая эту систему, для
nk
C и
nk
D найдём
следующие значения:
[
]
[]
n
2
nk21nnnk22
2nknn1nnnk22
nk
bq)ar(ba
RR)ar(ba
C
γ⋅α⋅−⋅τ⋅−+
⋅α⋅γ⋅τ+⋅τ⋅−+
=
∗∗∗
∗∗
(8)
и
+
τ
⋅⋅
⋅
−⋅+
=
∗
∗∗
2
n
nknk2
nnk22
nk
R
Cab
)ar(ba
1
D
(9)
Через q
1
, R
1
и R
2
в формулах (8) и (9) обозначены выражения:
)ar()ar(mq
nnkn1nk,1n1n1nnkk,1n1n1
+
γ
+
−
τ
γ
+
α
γ
−=
−−−−−−
;
()
+
ελ
−
τελ
⋅−τγ−αγ=
−−
−
−−−−−−
n
2
k
nk
1n1n
2
k
k,1n
1nk,1n1n1nnkk,1n1n1
A
A
arSR
k,1n
1n
2
k
k,1n1n1n
n
2
k
nknn
L
Aa2
Aa2
−
−
−−−
+
ελ
γ
−
ελ
γ
+ ; (10)
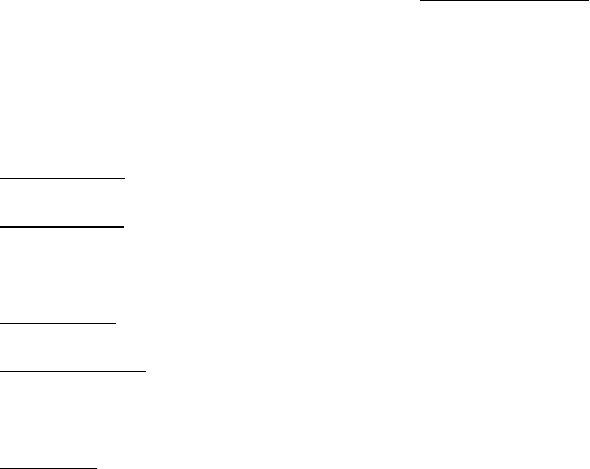
245
(
)
nn
2
k
nkn
*
2
*
2
k22
Aab2a
FR
τ⋅ε⋅λ
⋅−
+=
)
(11)
В заключение дадим краткое описание алгоритма по расчёту потенциала
поля в прямоугольной многослойной области.
Во-первых
, вычисляются коэффициенты m
2k
и S
2k
по формулам (2) и (3).
Во-вторых
, вычисляются прогоночные коэффициенты m
ik
и S
ik
для i =
3,4,…,n по рекуррентным формулам (6) и (7).
В-третьих
, вычисляем коэффициенты С
nk
и D
nk
по формулам (8) и (9).
В-четвёртых
, вычисляем коэффициенты C
n-1,k
; C
n-2,k
; C
n-3,k
; …; C
2k
; C
1k
по
рекуррентным формулам (5).
В-пятых
, по формулам (6.1) через С
ik
последовательно вычисляем D
1k
;
D
2k
;…; D
n-1,k
.
После этого остаётся подставить вычисленные коэффициенты С
ik
и D
ik
в
ряды (5.1) и с их помощью вычислить потенциалы поля по формулам (4.1) для
каждого слоя g
i
в многослойной области.
6.8. Применения развитой теории
Изложенная теория расчёта статического поля в прямоугольной
многослойной области может быть применена к решению следующих
конкретных задач: 1). Для анализа точности моделирования многослойных сред
(MC-сред) из периодически повторяющихся изотропных слоёв с разными
проницаемостями анизотропно-однородными моделями Оллендорфа. 2). Для
приближённого расчёта статического поля в неоднородной вдоль оси х
прямоугольной области с произвольным законом изменения Г
1
(х). В этом
случае ось х разбиваем на частичные отрезки (диаметр разбиения будет зависеть
от поставленной точности расчётов). Затем заменяем на частичных отрезках
Г
1
(х) на экспоненциальный закон изменения проницаемости. Подчеркнём, что
на концах каждого частичного отрезка значения Г
1
(х) и найденные из
аппроксимирующего закона будут совпадать. После осуществлённой
аппроксимации для расчёта поля в неоднородной среде применяем изложенную

246
методику расчёта поля в МС-среде. 3). Для расчёта при аналогичных краевых
условиях поля в многослойной криволинейной области, ограниченной
координатными линиями какой-либо изотермической системы координат. При
этом границами слоёв должны быть координатные линии одно из семейств.
Возможность применения развитой теории к расчёту полей в таких
многослойных областях основана на том, что в изотермических координатах
уравнение для потенциала и граничные условия принимают аналогичный для
случая декартовых координат вид.
Для иллюстрации применения развитой теории далее приводятся три
конкретных примера, имеющих самостоятельное практическое значение.
В первом примере
анализ полученного решения, основанный на способе
послойного расчёта поля, выявил эффекты присущие только МС-средам.
Доказано, что широко применяемый на практике метод однородно-
анизотропного эквивалентирования МС-сред, основанный на идее
Оллендорфа [252], не способен уловить эти особенности.
Во втором и третьем примерах
показано, как на основе развитой в этой
главе теории и предложенной операции интегрального эквивалентирования
можно найти распределение потенциала поля в изотропных неоднородных
средах. Проанализированы возможные числовые погрешности.
6.8.1 Метод интегрального эквивалентирования кусочно-неоднородных сред.
Однородно-анизотропное эквивалентирование. Рассмотрим случай, когда
область G заполнена средой, главные проницаемости которой равны Г
1
= γ ⋅ f(x)
и Г
2
= εγ ⋅ f(x), где ε, γ - постоянные, f(x) – кусочно-непрерывная на отрезке MD
(рис.66) функция и плотность источников Ω (y) ≡ 0. Тогда уравнение (1.4) будет
иметь два частных решения, зависящих только от одной из координат. Первое ϕ
= ϕ
1
(х), и второе ϕ = ϕ
2
(y), где
∫
∫
⋅ϕ−ϕ+ϕ=ϕ
b
a
x
a
aba1
)x(f
dx
)x(f
dx
)()x(
;
ab
ay
)()y(
aba2
−
−
⋅ϕ−ϕ+ϕ=ϕ
.

247
Физический смысл этих решений в том, что они описывают однородные поля
(в теории фильтрации – поступательные потоки), в первом линии тока
направлены вдоль оси х, а во втором – вдоль у. Постоянные ϕ
a
и ϕ
b
–
значения потенциала на прямых х = а, х = b (в первом) и у = а, у = b (во
втором). Поток однородного поля в первом случае через нормальный к нему
отрезок x = const, 0 < y < h равен
∫
∫
ϕ−ϕγ
−=ν=
b
a
ab
h
0
x1
)x(f
dx
)(h
dyQ
, (1)
а во втором случае через нормальный к нему отрезок у = const, a < x < b
равен
∫∫
⋅
−
ϕ−ϕεγ
−=ν=
b
a
ab
b
a
y2
dx)x(f
ab
)(
dyQ
. (2)
Определение
: две физические среды с главными проницаемостями
Г
1
= γ⋅f(x), Г
2
= εγ⋅f(x) у первой и Г′
1
= γ′⋅f ′(x), Г′
2
= ε′γ′⋅f ′(x) у второй,
называются интегрально эквивалентными в прямоугольнике D = {a < x< b; 0
< y < h} если соответствующие потоки однородных полей в этих средах через
прямые х = const и у = const при одинаковых граничных условиях ϕ
a
и ϕ
b
будут равными, т.е. если Q
1
= Q′
1
и Q
2
= Q′
2
.
Приравнивая указанные потоки, получаем следующие выражения для
условия интегральной эквивалентности двух сред в прямоугольнике D:
∫∫
⋅=⋅
b
a
b
a
xf
dx
xf
dx
)(''
1
)(
1
γγ
;
∫∫
=
b
a
b
a
dxxfdxxf )(''')(
γεεγ
(3)
Приведём теперь важный для практики пример построения интегрально-
эквивалентной среды для заданной. Пусть заданная среда – многослойная,
составленная из чередующихся изотропных однородных слоёв с
проницаемостями γ
1
и γ
2
и с толщинами h
1
и h
2
. Тогда ε = 1, γ = 1,
++≤<+γ
+≤≤γ
=
2112
11
hhxhдля,
haxдля,
)x(f
aa
a
. Подберём для неё интегрально
эквивалентную однородную анизотропную среду с характеристиками γ′ = γ′
1
,

248
ε′ = γ′
2
/γ′
1
и f ′(x) = 1. Из решения системы уравнений (3) для γ′
1
и γ′
2
найдём,
что
21
2211
2
1221
2121
1
hh
hh
';
hh
)hh(
'
+
γ
+
γ
=γ
γ+γ
γ
γ
⋅
+
=γ . (4)
Формулы (4) выводились другим путём и применялись ранее при расчётах
физических полей в слоистых средах многими авторами. Например в [120-
122], анализируя линии тока фильтрационного течения в физически малой
окрестности и заменяя затем в ней истинную трубку тока течения на трубку
тока некоторого эквивалентного суммарного движения Е.С. Ромм тоже
приходит к формулам (4). Точно так же и Оллендорф [252]
электротехнические расчёты потенциальных полей в мелкослойчатых средах
выполняет с помощью (4) на однородно-анизотропных моделях МС-сред. На
самом же деле погрешности расчётов, полученные методом однородно-
анизотропной аппроксимации слоистой среды могут быть существенными.
Кроме того, однородно-анизотропная аппроксимация МС-среды не может
выявить свойства, присущие самим мелкослойчатым средам. Для
подтверждения этого приведём следующий пример 1. Рассмотрим случай,
когда прямоугольная область MBED (рис.66) заполнена чередующимися
однородными изотропными слоями одинаковой толщины h
1
= h
2
и с
проницаемостями γ
1
и γ
2
. Источники отсутствуют. Пусть на сторонах MD и
BE заданы однородные граничные условия ϕ = 0, на стороне DE
0
x
=
∂
ϕ
∂
, а на
стороне МВ
∑
π
⋅=ϕ
=
N
1k
k
MB
h
ky
sina
, (5)
где а
к
= const. Потенциал ϕ
ан
(х,у) для однородно-анизотропной модели будет
найден при тех же граничных условиях из уравнения (1.4), которое здесь
имеет вид
2
,
2
,
,
;0
yx
21
2
21
21
1
1
2
2
2
2
2
γ+γ
=λ
γ+γ
γγ
=λ
λ
λ
=ε=
∂
ϕ∂
ε+
∂
ϕ∂
. Точное решение
этой «анизотропной» краевой задачи такое:
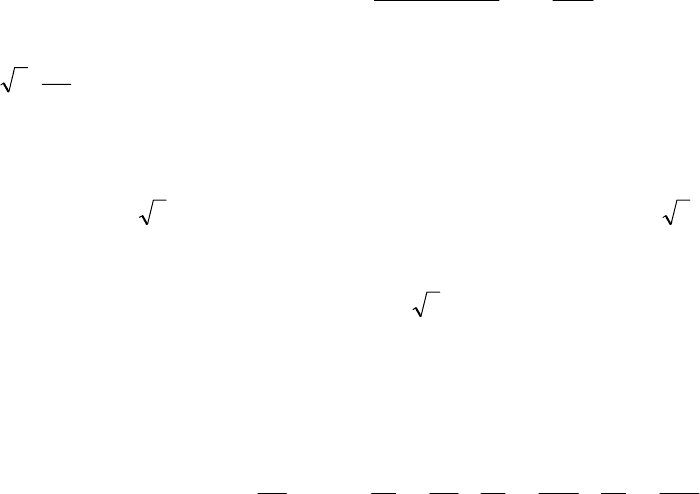
249
[
]
()
,
h
ky
sin
ch
)x(ch
a)y,x(
N
1k
k
k
kaн
π
⋅
β
−β
⋅=ϕ
∑
=
l
l
(6)
где
h
k
k
π
⋅ε=β
. С помощью (6) вычислим потоки Q
BE
, Q
MD
и Q
MB
векторного
поля
υ
r
через границы BE, MD и МB. Имеем:
()
[]
k
k
N
1k
k1
h
0
xMB
)1(1thady)y,0(Q −−⋅β⋅ελ=υ=
∑
∫
=
l
;
()
l
l
k
N
1k
k1
0
yMD
thadx)0,x(Q β⋅ελ=υ=
∑
∫
=
;
()
l
l
k
N
1k
k
k
1
0
yBE
tha)1(dx)h,x(Q β⋅−ελ−=υ=
∑
∫
=
Естественно, как и должно быть по уравнению неразрывности,
Q
MB
= Q
MD
+ Q
BE
. В контрольных расчётах граничное условие (5) имело вид
π
+
π
−
π
⋅ϕ=
π
⋅ϕ=ϕ
h
y5
sin
16
1
h
y3
sin
16
5
h
y
sin
16
10
h
y
sin)y(
0
5
0MB
,
а для безразмерных параметров задавались значения ϕ
0
= 100, ℓ = h = 10,
γ
1
= 10, γ
2
= 1. Распределение потенциала и потоки Q
MB
, Q
MD
и Q
BE
для
многослойной среды вычислялись по изложенной в этой главе теории.
Результаты вычислений для МС-среды и её однородно-анизотропной модели
представлены в таблице 6.1 и на графике (рис.68).
Из представленных в таблице 6.1 и на графике на рис.68 видно следующее.
1). С увеличением числа слоёв на отрезке MD слоистая среда по своим
свойствам приближается к однородно-анизотропной модели. Однако
скорость достижения «анизотропного состояния» различна в отношении
потоков и в отношении потенциала. Так погрешности в расчётах потоков в
МС-среде по соответствующим потокам в анизотропной модели будут менее
1% начиная с 50 слоёв и выше (т.е. когда толщина отдельного слоя
составляет 2% и менее от характерного размера ℓ расчётной области). В
расчётах же потенциала (и его градиента) погрешность однородно-
анизотропной модели долгое время остаётся большой. В частности,
погрешность в определении φ по анизотропной модели будет менее 1%, если
число слоёв на MD будет 80 и более (т.е. когда толщина отдельного слоя
будет менее ≈1,2% от характерного размера расчётной области). Таким
