Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.


210
Задача расчета удельного дебита скважины на основе уравнения (8) сводится к
отысканию такого его решения, которое удовлетворяло бы в области D гранич-
ным условиям
constQ;0 ==ψ=ψ
−+
γγ
. (11)
Здесь через γ обозначена некоторая в общем случае заранее неизвестная линия
тока течения, соединяющая границы П и С. В ряде случаев одну (или несколь-
ко) таких линий тока в области D удаётся указать исходя из геометрических со-
ображений. Поскольку, по свойствам функции тока ψ, при полном обходе в D
любой замкнутой кривой, охватывающей С, ψ получает приращение, равное Q,
то на одном “берегу” начальной линии тока γ функции ψ даётся значение, рав-
ное нулю, а на противоположном “берегу” этой же линии γ значение ψ должно
быть равно Q, что и записано в (11). Кроме граничных условий (11), решение
уравнения (8) должно удовлетворять ещё одному дополнительному условию:
т.к. на границах П и С заданы давления, то известна величина разности
СП
ϕ
−
ϕ
.
Поэтому решение (8) должно ещё удовлетворять требованию:
⋅
∂
ψ∂
−⋅
∂
ψ∂
⋅=⋅
∂
ϕ∂
+⋅
∂
ϕ∂
=ϕ=ϕ−ϕ
∫∫∫
ψ
−α
ψψ
dy
x
dx
y
vdy
y
dx
x
d
1
СП
(12)
где последний интеграл в (12) вычисляется по любой линии тока ψ = const, со-
единяющей П и С. (При выводе условия (12) использовали систему уравнений
(6)).
5.3.2 Вариационная формулировка краевых задач.
Отыскание точных аналити-
ческих решений краевых задач для нелинейных уравнений (7), (8) с граничны-
ми условиями (10) и (11), (12) зачастую приводит к серьёзным математическим
трудностям. Поэтому практически важными становятся методы приближённого
решения этих краевых задач. В данной работе приближённые решения строятся
путём перехода от сформулированных краевых задач к эквивалентным им ва-
риационным задачам. Для этого уравнения (7) и (8) будем рассматривать как
уравнения Остроградского [25] для функционалов
[
]
(
)
∫∫
⋅=ϕ
D
dxdyUFW (13)

211
и
[
]
(
)
∫∫
⋅=ψ
D
dxdyVGT , (14)
где
() ()
2
1
2
1
VVGиUUF
+α
α
α+
== (15)
Решение краевой задачи (7), (10) обеспечивает минимум функционалу (13) в
области D при тех же граничных условиях (10). Точно так же краевая задача
(8), (11) тоже определяет функцию ψ(x,y), дающую минимум функционалу T[ψ]
в области D при граничных условиях (11). Однако, в отличие от задачи для на-
хождения ϕ, появляющийся в решении неизвестный параметр Q надо будет оп-
ределять из дополнительного условия (12) через известное значение разности
СП
ϕ−ϕ .
Для решения задач минимизации функционалов W[ϕ] и T[ψ] наряду с де-
картовыми будем применять полярные и обобщённые полярные координаты. С
этой целью укажем вид функционалов (13), (14) в названных криволинейных
координатах.
В полярных координатах функционалы (13), (14) имеют вид:
[]
(
)
[
]
(
)
∫∫∫∫
θ⋅=ψθ⋅=ϕ
DD
rdrdVGT;rdrdUFW (16)
где
2
2
22
2
2
r
1
r
Vи
r
1
r
U
θ∂
ψ∂
⋅+
∂
ψ∂
=
θ∂
ϕ∂
⋅+
∂
ϕ∂
=
. (17)
Обобщённые полярные координаты t и θ удобно применять, когда задано одно-
параметрическое семейство замкнутых кривых
),t(rr
θ
=
, (18)
кривые которого, отвечающие различным значениям параметра t, не пересека-
ются друг с другом, т.е. r(t
1
,θ) ≠ r(t
2
,θ) при t
1
≠ t
2
. Такое семейство линий все-
гда можно построить, если бывают заданы уравнения границ С и П в полярных
координатах r и θ:
()
(
)
θ
=
θ=
ПC
rrиrr соответственно. В этом случае семейство
линий (18) можно задать уравнением вида

212
()
(
)
(
)
(
)
[
]
(
)
θ
⋅
α
−
+
θ
⋅
α
=
θ
=
CП
rt1rt,trr , (19)
где α(t) – некоторая монотонная непрерывная положительная функция, заданная
для t ∈ [0, 1] и удовлетворяющая условиям
(
)
(
)
11,00
=
α
=
α
. (20)
Тогда
()
(
)
θ
=θ
C
r,0r и
()
(
)
θ
=θ
П
r,1r . Если в (16) перейти к новым переменным t и θ,
то для функционала W[ϕ] получим выражение
[]
()( )
θ⋅
∂
∂
⋅θ⋅=ϕ
∫∫
dtd
t
r
,trUFW
D
, (21)
где
2
2
2
2
2
2
2
2
r
1
t
t
r
r
r
2
t
t
r
r
r
r
U
θ∂
ϕ∂
⋅+
θ∂
ϕ∂
⋅
∂
ϕ∂
⋅
∂
∂
⋅
θ∂
∂
⋅
−
∂
ϕ∂
⋅
∂
∂
⋅
θ∂
∂
+
=
(22)
Кроме координат t и θ, удобными для решения конкретных задач оказы-
ваются ещё и другие - обобщённые полярные координаты r и λ. Эти координа-
ты задаются с помощью выбора некоторого периодического по λ однопарамет-
рического семейства пучка кривых
(
)
λ
θ
=
θ
,r , (23)
с центром в некоторой точке внутри контура C. Если разность λ
1
- λ
2
равна пе-
риоду, то уравнения θ(r,λ
1
) и θ(r,λ
2
) будут определять одну и ту же кривую. В
дальнейшем для удобства будем выбирать стандартную нормировку по периоду
для λ:
()
(
)
πθ=θ 2,r0,r . Уравнения границ С и П области D, если семейство (23)
задано, всегда можно записать в новых координатах r и λ . Для этого подстав-
ляем (23) в уравнения
(
)
(
)
θ
=
θ
=
ПC
rrиrr и решаем их относительно r. В ре-
зультате получим уравнения границ С и П
(
)
(
)
λ
=
λ
=
ПC
rrиrr (24)
в новых координатах. Если в (16) перейти к новым переменным r и λ, то для
функционала T[ψ] получим выражение
[]
()
λ⋅
λ∂
θ
∂
⋅⋅=ψ
∫∫
drdrVGT
D
, (25)
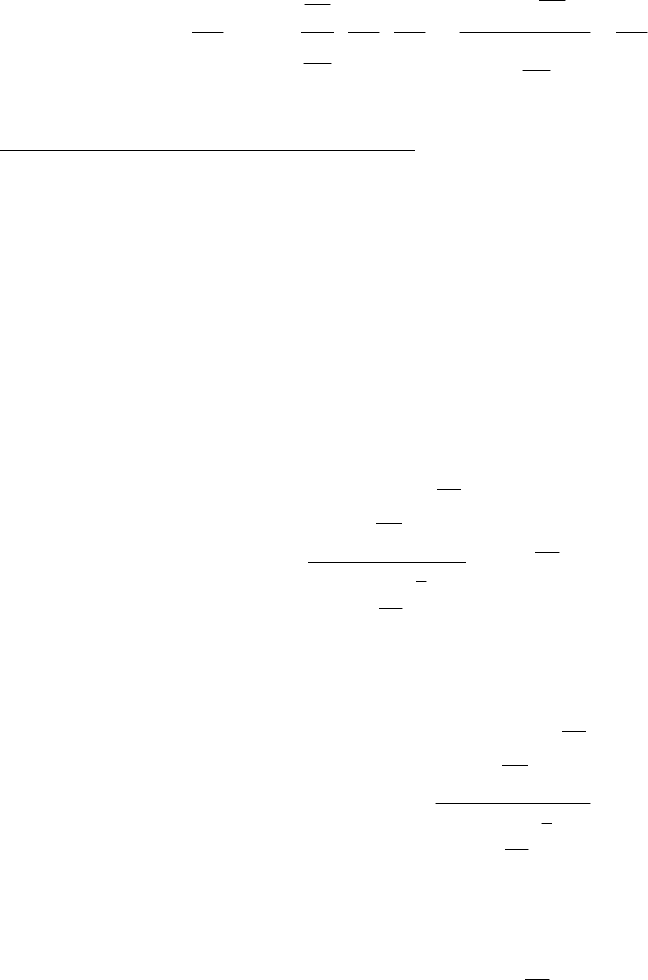
213
где
2
2
2
2
2
2
r
r
r1
r
r
2
r
V
λ∂
ψ∂
⋅
λ∂
θ∂
⋅
∂
θ∂
⋅+
+
λ∂
ψ∂
⋅
∂
ψ∂
⋅
λ∂
θ∂
∂
θ∂
⋅−
∂
ψ∂
=
(26)
5.3.3 Верхняя оценка дебита скважины.
Пусть уравнения границ С и П области
фильтрации D заданы уравнениями вида (18). Выберем сами некоторую систе-
му кривых, близких по форме к эквипотенциалям ϕ = const течения жидкости
от П к С. Для этого в уравнении (19) требуется задать конкретный вид функции
α(t) с соблюдением условий (20). Тогда на выбранной системе кривых, приня-
тых за эквипотенциали, функция ϕ = ϕ(t). На выбранной системе эквипотенциа-
лей функционал (21), с учетом формул (15) и (22), примет вид
[]
()
[]
∫∫
θ⋅ϕ
′
⋅
∂
∂
⋅
θ∂
∂
+
=ϕ
α
α+
α
α
α+
D
1
1
2
1
2
2
dtdt
t
r
r
r
r
W . (27)
Выполняя в (27) интегрирование по θ и обозначая через H(t) интеграл
()
∫
π
α
α
α+
θ⋅
∂
∂
⋅
θ∂
∂
+
=
2
0
1
2
1
2
2
d
t
r
r
r
r
tH
(28)
для W[ϕ] на пробном семействе эквипотенциалей (19) получаем выражение
[]
() ()
[]
dtttHW
1
0
1
⋅ϕ
′
⋅=ϕ
∫
α
α+
. (29)
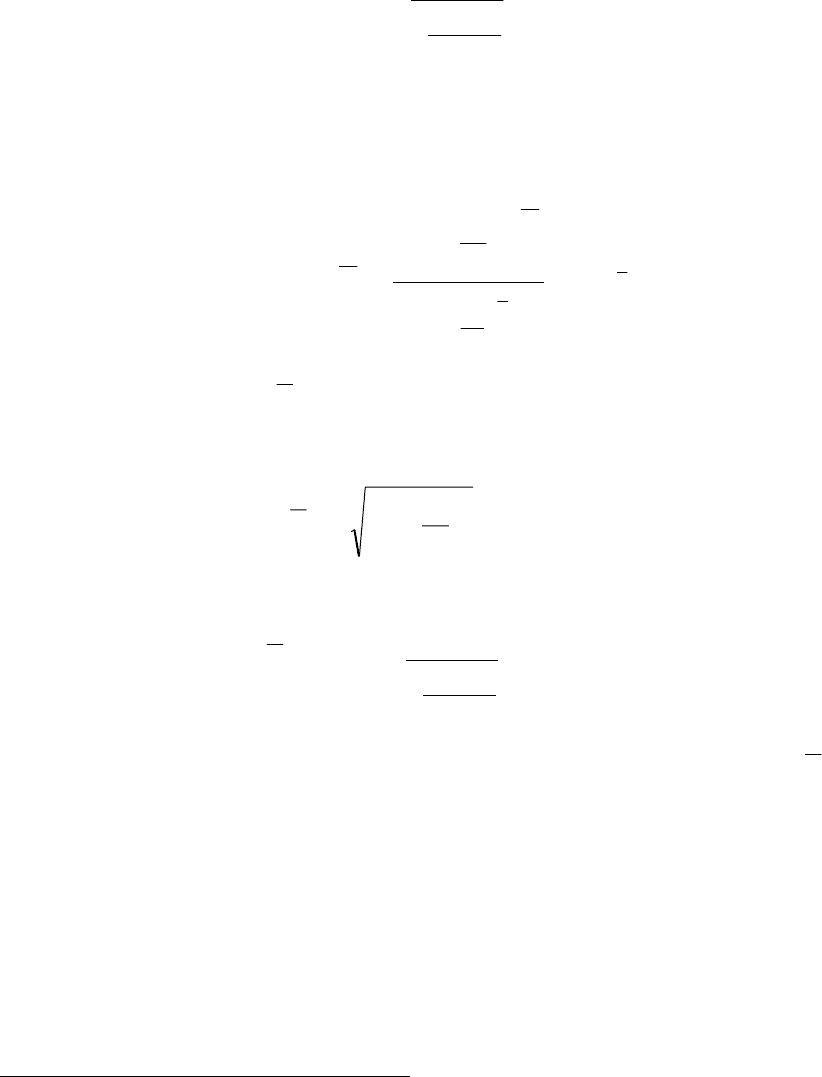
Решая уравнение Эйлера, для функционала (29) находим следующую экстре-
маль
() ()
[]
∫
ϕ+⋅⋅=ϕ
α−
t
0
C1
dttHCt
, (30)
21
4
которую принимаем в качестве искомого закона распределения потенциала ϕ.
Произвольную постоянную
1
C в (30) находим из граничных условий
(
)
C
0
ϕ
=
ϕ
и
()
П
1 ϕ=ϕ :
()
[]
∫
α
ϕ
−
ϕ
=
1
0
СП
1
tH
dt
С
. (31)
Теперь, когда функция ϕ найдена, можно вычислить дебит. Для этого вначале
вычисляем по формулам (9) и (22) скорость фильтрации на эквипотенциалях:
()
[]
α
α
α
α
ϕ
′
⋅
∂
∂
⋅
θ∂
∂
+
==
1
1
2
1
2
2
2
1
t
t
r
r
r
r
Uv . (32)
После этого находим дебит
Q , вычисляя интеграл вдоль всей эквипотенциали ϕ
= const:
∫
π
θ⋅⋅
θ∂
∂
+=
2
0
2
2
dv
r
rQ .
Опуская выкладки, запишем окончательный результат:
()
[]
∫
α
α
ϕ
−
ϕ
=−=
1
0
ПC
1
tH
dt
CQ
. (33)
Подчеркнём, что найденная с помощью формулы (33) величина дебита
Q будет
завышенной по сравнению с точным решением. Это объясняется тем, что при
расчёте потенциала ϕ мы заранее выбрали некоторую систему кривых (19), ап-
проксимирующих сетку эквипотенциалей. А, как известно [108], введение ис-
кусственных эквипотенциалей в фильтрационное течение приводит к увеличе-
нию полного фильтрационного потока.
5.3.4 Нижняя оценка дебита скважины.
Снова будем рассматривать фильтраци-
онное течение от П к С в области D. Однако теперь зададимся некоторой ап-
проксимацией линий тока. С этой целью выберем какое - нибудь однопарамет-
рическое семейство кривых (23), линии λ = const которого и примем за линии

215
тока. Как известно [108], введение искусственных линий тока в фильтрацион-
ное течение приводит к уменьшению полного фильтрационного потока. Поэто-
му расчёт дебита скважины путём аппроксимации линий тока приведёт к зани-
женному по сравнению с точным значению дебита
Q . Функция тока ψ на вы-
бранном семействе (23) будет функцией одного переменного ψ = ψ( λ), и по-
этому функционал T[ψ] согласно (25) и (26) примет вид:
[]
()
[]
∫∫
λ⋅⋅λψ
′
⋅
λ∂
θ∂
⋅
∂
θ∂
⋅+
=ψ
α+
α
α+
D
1
2
1
2
2
ddr
r
r
r1
T . (34)
Выполняя в (34) интегрирование по r и обозначая
()
()
()
∫
λ
λ
α
α+
⋅
λ∂
θ∂
⋅
∂
θ∂
⋅+
=λ
П
C
r
r
2
1
2
2
dr
r
r
r1
L , (35)
для T[ψ] на пробном семействе линий тока получим выражение
[]
() ()
[]
λ⋅λψ
′
⋅λ=ψ
α+
π
∫
dLT
1
2
0
. (36)
Решая уравнение Эйлера для функционала (36) совместно с условиями (11), ко-
торые примут вид ψ(0) = 0, ψ(2π ) =
Q , для функции тока ψ(λ) получим зна-
чение:
()
()
[]
∫
λ
α
λ
λ
⋅=λψ
0
1
1
L
d
C
, (37)
где
()
[]
∫
π
α
λ
λ
=
2
0
1
1
L
d
Q
C
. (38)
Подставляя найденное выражение функции тока ψ(λ) в формулу (12) и выпол-
няя расчёты, получим, что постоянная
1
C в формуле (5) равна
()
α
ϕ−ϕ=
1
ПC1
C . (39)
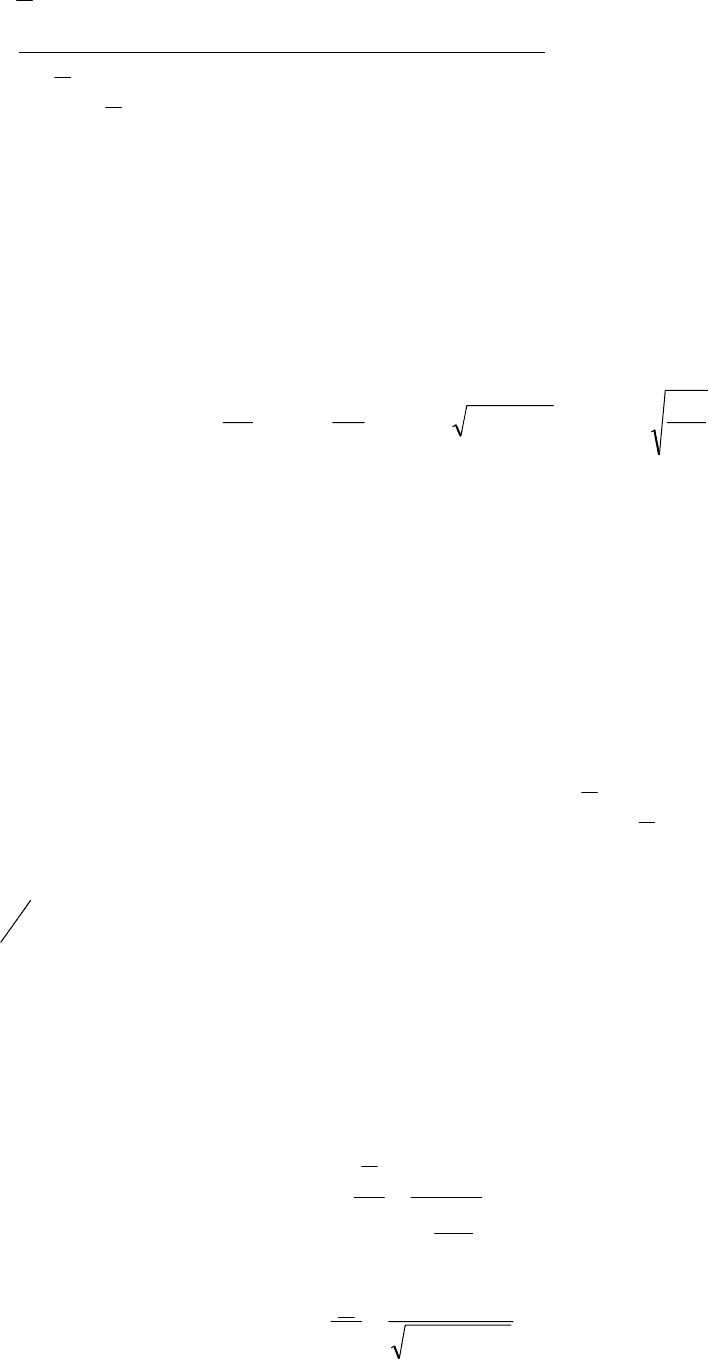
216
Теперь по формулам (35), (38) и (39) можно будет вычислить нижнюю оценку де-
бита
Q .
5.3.5 Дебит скважины в пласте овальной формы.
Применим полученные выше
оценки
Q и Q для расчёта дебита эксплуатационной скважины, работающей в
пласте овальной формы. С этой целью в качестве однопараметрического семей-
ства линий (7) рассмотрим семейство вида
(
)
(
)
[
]
θ⋅⋅−
⋅+⋅−⋅=θ
costa
00
e1t1Rr,tr , (40)
где
210
RиR,r – три положительных параметра
210
RRr0 <
<
<
, через которые вы-
числяются коэффициенты R
0
и a в (40) по формулам
=⋅===
10
20
20100
0
2
20
0
1
10
R
R
a;RRR;
r
R
R;
r
R
R
ln (41)
При t = 0 уравнение (40) будет задавать круговой контур скважины радиуса
0
r ,
а при t = 1 - овальную форму контура питания. Естественно, параметры
210
RиR,r должны быть подобраны так, чтобы кривые
()()
θθ ,trи,tr
21
при
21
tt
≠
не пересекались бы друг с другом. Последнее условие накладывает определён-
ные ограничения на диапазон изменения геометрических параметров
210
RиR,r ,
задающих размеры и форму области фильтрации. Опуская выкладки, приведём
лишь окончательные результаты расчётов оценок
QиQ по формулам (33) и
(38) для
случая линейного режима фильтрации (в (2) коэффициент α = 1,
;
k
B
µ
= µ - динамическая вязкость жидкости, k - коэффициент проницаемости
среды) и для
случая фильтрации по закону А.А. Краснопольского (в (2) коэффи-
циент α = 2).
Для дебита круговой скважины, работающей в данном пласте при
линей-
ном режиме фильтрации
, получены следующие оценки:
(
)
()
;
th
dt
R
Q
Q
1
0
10
0
∫
=
ln
(42)
(
)
;
aR
Q
Q
2
0
2
0
−
=
ln
Rln
10
(43)

217
где
(
)
()
;
PPk2
Q
СП
0
10
Rln⋅µ
−
⋅
⋅
π
= (44)
() ()()
;
)t(ga1R1R
)t(gta
)t(ga1R
)t(g
)t(h
22
2
00
22
22
2
0
⋅−−+−
⋅
+
⋅−−
=
(45)
(
)
1t1R)t(g
0
+
⋅
−
=
. (46)
Ранее В.Л. Даниловым в [48] для режима
линейной фильтрации рассчитывались
дебиты скважин в пластах с произвольным контуром питания. При этом расчёт
дебита круговой одиночной скважины в [48] сводился к отысканию параметра
двухсвязности области фильтрации, что в свою очередь требовало решения не-
линейного сингулярного интегрального уравнения. Решение последнего удава-
лось найти в очень редких случаях. В качестве примера применения своей тео-
рии В.Л. Данилов приводит расчёт дебита круговой скважины в пласте с конту-
ром питания, совпадающим (с точностью до обозначений) с (40) при t = 1. В ча-
стности, в [48] выполнены расчёты для двух, уже приводившихся в §5.1 приме-
ров (примеры 2 и 3). Приведём теперь результаты расчётов дебитов этих же
скважин для линейного режима фильтрации по предлагаемой методике.
Для условий примера №2 из §5.1
находим, что R
10
= 5,458; R
20
= 8,143;
9046,0
Q
Q
0
= ; 8996,0
0
=
Q
Q
. В качестве расчётного значения Q/Q
0
примем среднее
арифметическое
0
Q2
QQ +
и найдём, что Q/Q
0
= 0,9021. Для исходных данных этого
базисная величина Q
0
(которую для единицы длины скважины рассчитываем по
(44)) равна 800,05 м
3
/сутки. Стало быть, по В.Л. Данилову Q/Q
0
= 0,9033 , что
отличается от нашего результата на 0,13%.
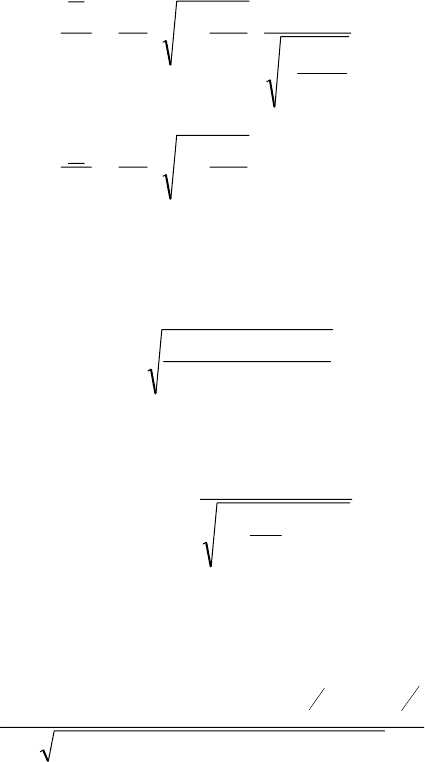
Для условий примера №3 из §5.1
находим, что R
10
= 6065; R
20
= 16487;
9471,0
Q
Q
;9566,0
Q
Q
00
== . Принимая за расчётное значение дебита Q/Q
0
среднее
арифметическое, получим Q/Q
0
= 0,9519. Для этого базисная величина Q
0
=
311,95 м
3
/сутки, и поэтому, по В.Л. Данилову Q/Q
0
= 0,9553, что отличается от
нашего результата на 0,36%.
218
Для дебита этой же скважины, но работающей в условиях нелинейного
режима фильтрации по закону А.А. Краснопольского
, получены оценки:
()
;
th
dt
1
R
1
1
2
1
Q
Q
1
0
2
100
∫
⋅−⋅
π
=
(47)
;d)(g
R
1
1
2
1
Q
Q
2
0
100
∫
π
θ⋅θ⋅−⋅
π
=
(48)
Здесь, в отличие от предыдущего случая, выбрана другая базисная величина
0
Q ,
а именно:
(
)
()
.
rRB
pprR
2Q
01
CП01
0
−⋅
−⋅⋅
⋅π=
⋅
(49)
Функции h(t) и g(θ) в (47) и (48) находятся по формулам
,
e
R
1
1
1
)(g
cosa
0
θ⋅
⋅−
=θ
(50)
,d),t(f)t(h
2
0
∫
π
θ⋅θ=
(51)
()
[]
(
)
()( )
.
cosacosta11R
esinta11t1R
),t(f
0
2
costa
4
3
222
0
θ⋅−θ⋅⋅−⋅−
⋅θ⋅+⋅+⋅−
=θ
θ⋅⋅−
(52)
Таким образом, предлагаемый в этом параграфе метод расчёта дебитов
одиночных скважин имеет приемлемую для практики точность расчётов, и,
кроме того, по сравнению с [48] он более удобен в вычислительном отношении,
так как требует лишь методов численного интегрирования. Наконец, предло-
женный метод в отличие от [48] применяется не только в случае линейного ре-
жима фильтрации, но и для нелинейной фильтрации со степенными законами
(2).
5.4 Расчёт дебитов и поля давления для группы скважин (многоскважинная
система без учёта ПЗС)
Одним из важных для нефтепромысловой практики вопросов, является
определение оптимального числа скважин по отношению к их суммарному де-
219
биту. В этом и следующих параграфах рассматриваются 1) общие методы ре-
шения такой задачи и 2) приводятся конкретные числовые примеры расчётов
суммарного дебита n скважин, имеющие главным образом иллюстративное
значение и предназначенные для их использования в чтении спецкурсов по
приложениям методов ТФКП в механике сплошных сред студентам нефтегазо-
вых специальностей.
5.4.1 Постановка задачи и общий метод решения.
Рассмотрим теперь задачу об
интерференции n скважин, эксплуатирующих неоднородный пласт с проницае-
мостью (1.1). Область фильтрации D ограничена контуром питания П, на кото-
ром потенциал ϕ принимает заданное значение
const
П
П
=ϕ=ϕ , (1)
а на круговых контурах
(
)
(
)
2
k
2
k
2
kk
ryyxx:С =−+− скважин с радиусами r
k
(где k
= 1,2, … ,n ) заданы значения
const
k
C
k
=ϕ=ϕ
. (2)
Требуется рассчитать в области D поле давления и удельные дебиты Q
k
каждой
скважины. Представим поэтапное решение данной задачи.
1 этап. Каким - либо численным методом решаем n взаимно независимых
краевых задач:
(
)
[
]
() ()
()
=
−=
=
n,...,2,1k
y,x,y,xgy,xf
0y,xfL
П
kk
П
k
k
, (3)
где g(x,y,x
k
,y
k
) – известное 1-ое фундаментальное решение уравнения (1.2).
2 этап. Строим вспомогательные функции – функции Грина ϕ
k
(x,y):
(
)
(
)
(
)
=
+=ϕ
n,...,2,1k
y,xfy,x,y,xgy,x
kkkk
. (4)
Каждая из функций Грина ϕ
k
(x,y) удовлетворяет (по построению) уравнению (1.2)
и граничному условию
.0
П
k
=ϕ (5)
