Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.


200
диусом τ
2
или круговым контуром с радиусом τ
1
и с центром на оси Ox в точке
(τ
1
−τ
2
, 0) (рис.57). В первом случае дебит скважины рассчитывается по формуле
Дюпюи:
(
)
2
.
ln
2
τ
ϕ
ϕ
π
ПC
прибл
Q
−
= . (22)
Во втором случае - по формуле дебита круговой скважины в эксцентричном
круговом пласте [41, 48], которая в принятых здесь обозначениях запишется в
виде:
(
)
−
−
=
1
2
2
.
2ln
2
τ
τ
τ
ϕ
ϕ
π
ПC
прибл
Q . (23)
Вычислительные эксперименты по исследованию погрешностей приближённых
формул (22) и (23) позволили сделать следующий вывод. В любом вытянутом
выпуклом овальном пласте, имеющем одну ось симметрии, в котором: 1) сква-
жина расположена на оси симметрии и, 2) ближайшее расстояние τ
2
от скважи-
ны до контура питания вдоль оси симметрии меньше расстояния τ
1
от скважи-
ны до контура питания в направлении, перпендикулярном к оси симметрии
()
12
τ
τ
< , дебит скважины следует вычислять по формуле (23). Погрешность
приближенной формулы (23), как показал вычислительный эксперимент, не
превышает 2,7% (для параметров τ
0
≤40 и τ
1
≤28). Если же τ
0
и τ
1
будут прини-
мать значение большее 100, то относительная погрешность будет составлять
0,85% и менее.
Для подтверждения справедливости сделанного вывода применим фор-
мулу (23) к расчёту дебитов скважин в овальных пластах, рассмотренных в ра-
боте В. Л. Данилова [48].
Пример № 2.
Уравнение контура питания :
θ⋅−
⋅=
cos2,0
e10000r (метров), ра-
диус скважины r
с
= 1500 метров (так называемая “укрупнённая” скважина, по-
нятие которой введено В.Л. Даниловым для оценки суммарного дебита группы

201
скважин), мощность пласта h = 5 метров, давление на контуре питания p
п
= 160
атм., давление на скважине p
с
= 155 атм., проницаемость k = 1 дарси, вязкость µ
= 1 сантипуаз. Для этих данных в [48] получено значение дебита
Q = 722,7 м
3
/сутки.
Для условий этого примера находим, что полярные радиусы точек пере-
сечения контура питания с осями координат для углов θ равных 0
0
, 90
0
и 180
0
соответственно равны r
1
= 8187,307 м, r
2
= 10000 м и r
3
= 12214,028 м. Поэтому
параметры τ
0
, τ
1
и τ
2
будут равны: τ
0
= r
3
/r
скв
= 8,142853…, τ
1
= r
2
/r
скв
= 6,6666…
и τ
2
= r
1
/r
скв
= 5,458205….Теперь по формуле (23) легко подсчитать, что удель-
ный дебит скважины q = 145,707 м
3
/сутки, а массовый дебит
Q = h×q = 728,54 м
3
/сутки. Стало быть, относительная погрешность расчётов по
формуле (23) составила 0,81%.
Пример №3.
Исходные данные:
θ⋅−
⋅=
cos5,0
e1000r (метров), r
c
= 0,1 (м), h = 5
(м), p
п
= 150 атм., р
с
= 130 атм., k = 0,5 дарси , µ = 1 сантипуаз. Здесь в [48] по-
лучено значение дебита Q = 298 м
3
/сутки. Для перечисленных условий поляр-
ные радиусы точек пересечения контура питания с осями координат для углов θ
равных 0
0
, 90
0
и 180
0
соответственно равны r
1
= 606,531 м, r
2
= 1000 м и r
3
=
1648,721 м. Поэтому параметры τ
0
, τ
1
и τ
2
имеют значения:
τ
0
= r
3
/r
скв
= 16487,21…, τ
1
= r
2
/r
скв
= 10000,00… и τ
2
= r
1
/r
скв
= 6065,31….Теперь
по формуле (23) найдём, что удельный дебит скважины q = 60,101 м
3
/сутки, а
массовый дебит Q = h×q = 300,50 м
3
/сутки. Стало быть, относительная погреш-
ность расчётов по формуле (23) составила 0,84%.
Как видим, рассмотренные примеры подтверждают справедливость вы-
водов относительно условий применения приближённой формулы (23) к расчё-
ту дебитов в пластах овальной формы с одной осью симметрии.
Разумеется, область применения предложенного метода не ограничивает-
ся приведёнными примерами.
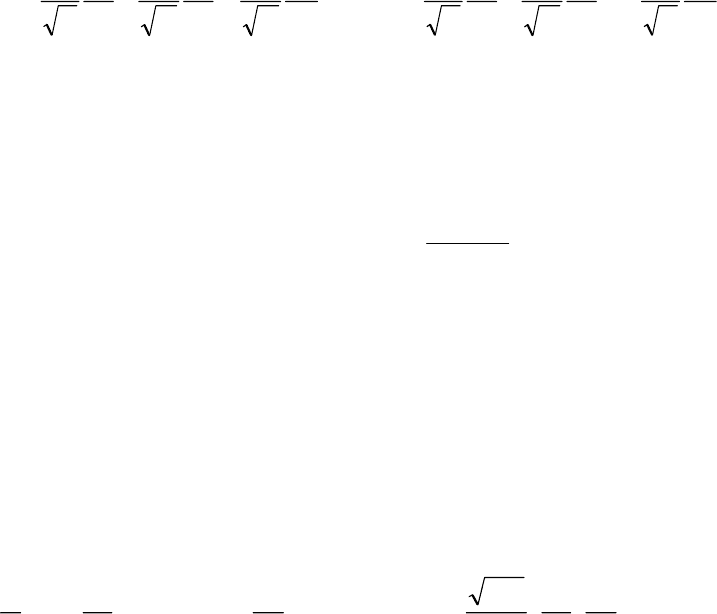
202
5.2. Применение вариационных методов для расчёта двусторонних оценок
дебитов одиночных скважин в анизотропных средах при линейном режиме
фильтрации
Сложность задач расчёта дебита и поля давления для скважин, эксплуати-
рующих анизотропные пласты, по сравнению с изотропными сильно возраста-
ет. Поэтому для анизотропных сред важную роль играют приближённые мето-
ды расчёта дебитов скважин. Автор в этом параграфе выводит формулы для
расчёта верхних и нижних оценок дебитов скважин на основе вариационных
методов, названных в работе методами пробных эквипотенциалей и пробных
линий тока.
Линейная плоско-параллельная фильтрация жидкости в анизотропно- не-
однородных средах описывается функциями ϕ(ξ,η) и ψ(ξ,η), удовлетворяющим
системе уравнений (2.3.2′). Перепишем эту систему совместно с формулами для
проекций скорости фильтрации:
ξ∂
ψ
∂
−=
η∂
ϕ∂
+
ξ∂
ϕ
∂
=
η∂
ψ
∂
=
η∂
ϕ
∂
+
ξ∂
ϕ∂
=
E
1
G
c
E
b
v;
G
1
G
b
E
a
v
21
. (1)
Здесь ξ,η - расчетная ортогональная криволинейная система координат, E и G –
коэффициенты 1-ой квадратичной формы, v
1
и v
2
– проекции скорости фильтрации
на ξ и η – координатные линии, ψ(ξ,η) - функция тока,
()
µ
⋅
−=ηξϕ
Pk
,
0
(2)
P – приведённое давление, k
0
- некоторая постоянная с размерностью проницаемо-
сти, a, b, c - компоненты безразмерного тензора проницаемости, вычисляемые че-
рез задаваемый закон распределения главных направлений анизотропии (ГНА) и
главные проницаемости λ
1
(ξ,η) и λ
2
(ξ,η). Расчёт a,b,c осуществляется по форму-
лам (см. приложение 2):
()
201020
2
10
2
ppEG
b;
p
E
p
G
1
a λ−λ⋅
η∂
∂
⋅
ξ∂
∂
⋅
∆
=
λ⋅
η∂
∂
⋅+λ⋅
ξ∂
∂
⋅
∆
=
(3а)

203
22
20
2
10
2
p
E
p
G;
p
G
p
E
1
c
η∂
∂
⋅+
ξ∂
∂
⋅=∆
λ⋅
ξ∂
∂
⋅+λ⋅
η∂
∂
⋅
∆
=
. (3б)
В формулах (3а) и (3б) p = p(ξ,η) - функция, нормали к линиям уровня которой
определяют 1-ое ГНА с главной проницаемостью λ
1
(ξ,η), а касательные к
p(ξ,η) = const определяют 2-ое ГНА с главной проницаемостью λ
2
(ξ,η);
=
10
λ
0
1
k
λ
и
0
2
20
k
λ
λ
= – безразмерные главные проницаемости. Отметим, что в
соответствии с (3),
2010
2
bca λ⋅λ=−⋅ . (4)
Для сокращения дальнейших записей обозначим
).,(k
2010
ηξ=λλ
⋅
(5)
Путем перекрестного дифференцирования, для функций ϕ(ξ,η) и ψ(ξ,η) из сис-
темы (1) получаем уравнения
0
G
E
cbb
E
G
a =
η∂
ϕ∂
⋅⋅+
ξ∂
ϕ∂
⋅
η∂
∂
+
η∂
ϕ∂
⋅+
ξ∂
ϕ∂
⋅⋅
ξ∂
∂
(6)
и
0
G
E
),(k
c
),(k
b
),(k
b
E
G
),(k
a
2222
=
η∂
ψ∂
⋅⋅
ηξ
+
ξ∂
ψ∂
ηξη∂
∂
+
η∂
ψ∂
⋅
ηξ
+
ξ∂
ψ∂
⋅⋅
ηξξ∂
∂
(7)
В частном случае для однородных анизотропных сред (λ
1
= const и
λ
2
= const), выбирая
210
k λλ= = const, получаем, что k(ξ,η) ≡ 1. Поэтому урав-
нения (6) и (7) совпадут, а система уравнений (1) будет системой уравнений
Бельтрами. Это, согласно §2.4, позволяет для решения краевых задач фильтра-
ции в однородно-анизотропных средах применять методы теории аналитиче-
ских функций комплексного переменного.
5.2.1. Метод пробных эквипотенциалей.
Рассмотрим теперь следующую крае-
вую задачу для уравнения (6) в двухсвязной области D, ограниченной кусочно–
гладкими замкнутыми кривыми C (внутренняя граница) и П (внешняя граница):

20
4
const ;
п
П
=ϕ=ϕ=ϕ=ϕ иconst
с
С
. (8)
Граничные условия (8) появляются в задачах расчета дебитов скважин, расчета
удельной конденсаторной ёмкости в электростатике, расчета тепловых потерь в
теплопроводности. Уравнение (6) можно рассматривать как уравнение Остро-
градского [25] для функционала
[]
∫∫
η⋅ξ⋅
η∂
ϕ∂
⋅⋅+
η∂
ϕ∂
⋅
ξ∂
ϕ∂
⋅+
ξ∂
ϕ∂
⋅⋅≡ϕ
D
22
dd
G
E
cb2
E
G
aW
(9)
Как известно [25], краевая задача (6), (8) эквивалентна задаче минимизации в
области D функционала (9) при тех же граничных условиях (8). Выберем сис-
тему ортогональных координат ξ, η так, чтобы координатные линии
0
ξ
ξ
=
и
01
ξ
ξ
ξ
>= совпадали с границами C и П соответственно. Остальные линии ξ =
const будут представлять собой замкнутые кривые, охватывающие в области D
границу C. При полном обходе кривой ξ = const вторая координата η будет по-
лучать некоторое приращение
0
η
. Поэтому в области D координаты ξ,η будут
изменяться в пределах
10
ξ
ξ
ξ
≤
≤ и
0
0
η
η
≤
≤
, причем
(
)( )
0
,0,
η
ξ
ϕ
ξ
ϕ
= . Задачу ми-
нимизации функционала (9) будем решать приближенно, принимая систему ко-
ординатных линий ξ = const за эквипотенциали – пробные эквипотенциали те-
чения. Если выбранная система координат ξ, η окажется такой, что линии ξ =
const совпадут с действительными эквипотенциалями, то получим точное ре-
шение задачи. В общем случае, когда линии ξ = const дают искаженные эквипо-
тенциали течения, при расчете полного фильтрационного притока жидкости к
границе C получим завышенное по сравнению с точным значение. Завышение
притока вызывается тем, что эквипотенциали с гидродинамической точки зре-
ния – бесконечно узкие криволинейные полоски, заполненные свободной жид-
костью. Поэтому внесение в область фильтрации D сетки искусственных экви-
потенциалей приводит к снижению фильтрационного сопротивления области D
и, следовательно, к завышению в ней фильтрационного потока. Функцию ϕ(ξ,η)
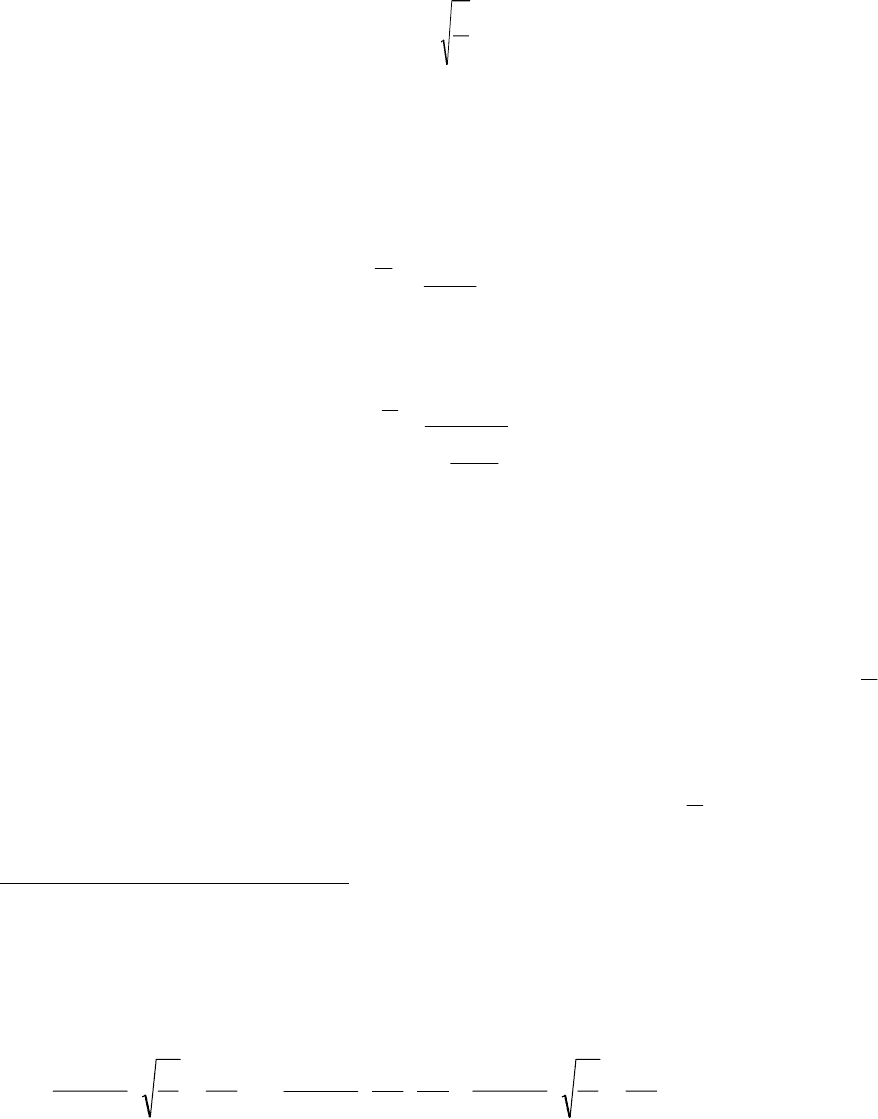
205
при сделанном выборе эквипотенциалей будем искать в виде
)(
ξ
ϕ
=ϕ
. Для
отыскания зависимости ϕ от ξ подставляем её в (9) и получаем:
[]
() ()
[]
ξξϕξϕ
ξ
ξ
dHW ⋅
′
⋅=
∫
2
1
0
, (10)
где обозначено
()
η
ξ
η
d
E
G
aH
∫
⋅⋅=
0
0
. (11)
Теперь минимизация функционала (9) свелась к минимизации функционала
(10) при условии
()
С0
ϕ=ξϕ и
(
)
П1
ϕ
=
ξ
ϕ
. Решая уравнение Эйлера [25] для функ-
ционала (11), получим:
()
∫
ξ
ξ
ϕ+
ξ
ξ
⋅−=ϕ
0
C
H
d
Q
, (12)
где постоянный множитель равен
()
∫
ξ
ξ
ξ
ξ
ϕ
−
ϕ
=
1
0
H
d
Q
ПС
. (13)
Теперь, когда приближенное значение ϕ найдено, можно рассчитать полный
фильтрационный приток жидкости от П к С в области D. Для этого вычисляем
интеграл по любой кривой ξ = const от нормальной составляющей скорости
фильтрации к этой кривой. Вычисляя такой интеграл получим, что
∫
ξ
=⋅ Qdsv
n
,
т.е. формула (13) определяет искомую величину фильтрационного потока. Ещё
раз подчеркнём, что истинное значение притока жидкости Q <
Q .
5.2.2. Метод пробных линий тока.
Рассмотрим теперь задачу расчета притока
жидкости к контуру C в двухсвязной области D на основе уравнения (7). Урав-
нение (7) будем рассматривать как уравнение Остроградского [25] для функ-
ционала
[]
() () ()
∫∫
η⋅ξ⋅
η∂
ψ∂
⋅⋅
ηξ
+
η∂
ψ∂
⋅
ξ∂
ψ∂
⋅
ηξ
+
ξ∂
ψ∂
⋅⋅
ηξ
=ψ
D
2
22
2
2
dd
G
E
,k
c
,k
b2
E
G
,k
a
T
. (14)

206
Снова выберем некоторую ортогональную систему координат ξ, η (в общем
случае, не совпадающую с той, которая применялась для расчёта верхней оцен-
ки
Q ) так, чтобы линии ξ = const были семейством простых замкнутых кривых,
а семейство линий η = const являлось бы пучком кривых с центром пучка внут-
ри контура C, т.е. ξ, η - топологический эквивалент полярной системы коорди-
нат на плоскости. Уравнения границ С и П в выбранной системе координат за-
пишутся в виде ξ = ξ
1
(η) и ξ = ξ
2
(η) соответственно. Линии η = const примем за
пробные линии тока течения. Если выбранная система η = const совпадёт с дей-
ствительными линиями тока, то получим точное решение задачи. В случае не-
совпадения - получим приближенное решение с заниженным по сравнению с
точным значением притока –значением
QQ
<
. Занижение притока вызывается
тем, что линии тока с гидродинамической точки зрения – непроницаемые ци-
линдрические поверхности, вдоль которых течёт жидкость. Внесение в область
D сетки искусственных линий тока может привести к появлению дополнитель-
ных преград для течения жидкости, и, значит, к завышению фильтрационного
сопротивления всей области. А это, в свою очередь, и вызывает занижение
фильтрационного притока от П к C. Поскольку полный обход любой η-
координатной линии расположенной в области D приводит к приращению
функции тока на величину -Q, равную искомому фильтрационному притоку, то
граничные условия для (14) задаём в виде
Q−==
==
0
;0
0
ηηη
ψ
ψ
, (15)
где η=0 и η=η
0
– значения координаты η на противоположных берегах некото-
рой зафиксированной пробной линии тока. Отыскание функции тока сводится к
определению минимума функционала (14) при граничных условиях (15). При
выбранной аппроксимации линий тока функция тока будет функцией одной пе-
ременной
(
)
η
ψ=ψ . Подставляя это выражение ψ в (14), для функционала T[ψ]
получим:
[]
() ()
[]
η⋅ηψ
′
⋅η=ψ
∫
η
dLT
2
0
0
, (16)
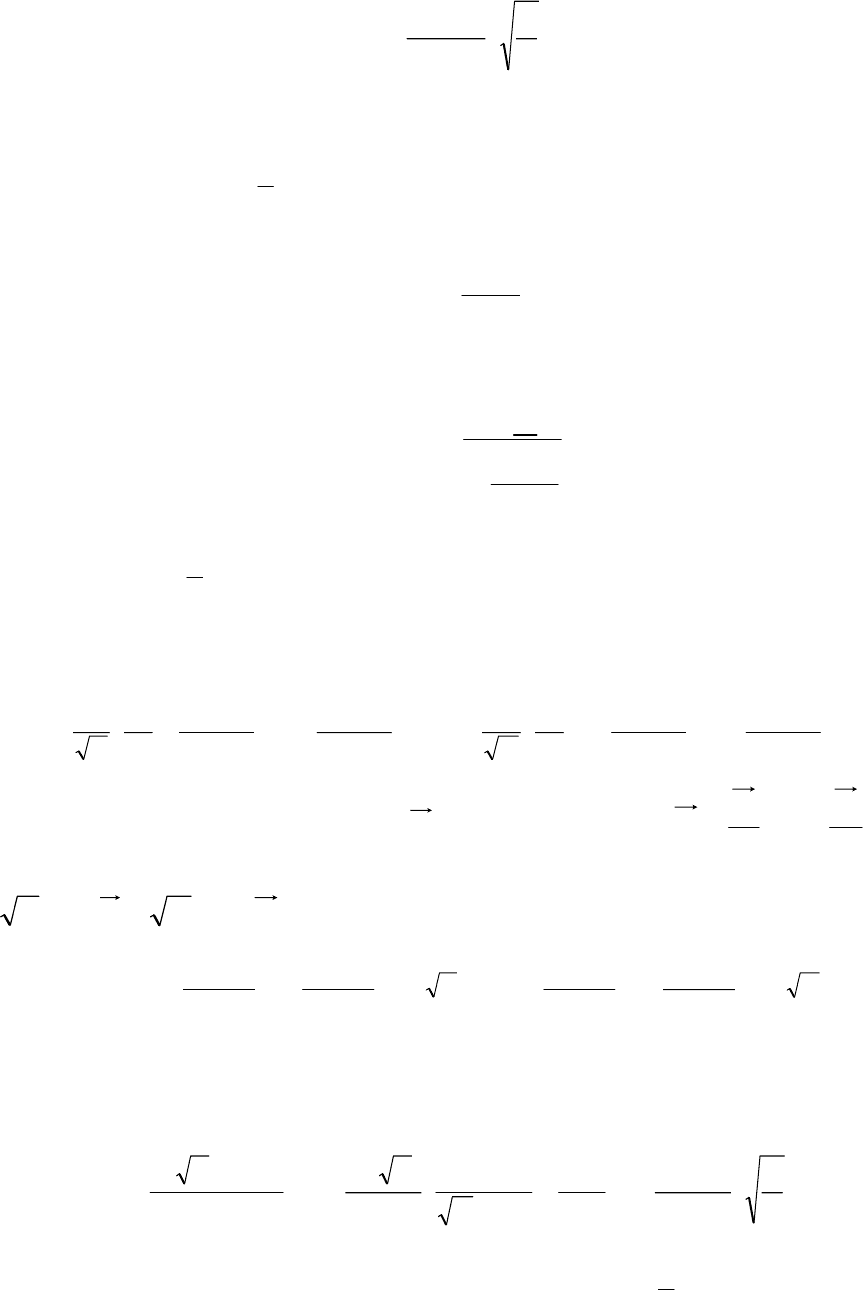
207
в котором через L(η) обозначено
()
()
()
(
)
∫
ηξ
ηξ
ξ⋅⋅
ηξ
=η
2
1
d
G
E
,k
c
L
2
. (17)
Теперь минимизация функционала (14) свелась к минимизации (16) при усло-
вии ψ(0) = 0 и
()
Q
0
−=η
ψ
. Решая уравнение Эйлера [25] для функционала (16),
получим:
()
()
∫
η
η
η
⋅=ηψ
0
1
L
d
C
(18)
где
()
∫
η
η
η
−
=
0
0
1
L
d
Q
C
. (19)
В силу того, что
Q неизвестно, постоянная С
1
тоже остается неизвестной. Для
отыскания С
1
будем исходить из того, что нам известна величина разности
СП
ϕ
ϕ
− , т.к. давления P
П
и P
С
заданы. Из уравнений движения (1) следует, что
() () () ()
2
2
1
2
2
2
1
2
v
,k
a
v
,k
b
G
1
;v
,k
b
v
,k
c
E
1
⋅
ηξ
+⋅
ηξ
−=
η∂
ϕ
∂
⋅⋅
ηξ
−⋅
ηξ
=
ξ∂
ϕ∂
⋅
. (20)
Но тогда
()
()
(
)
()
(
)
∫∫
ϕ=ϕ=ϕ−ϕ
П
С
П
С
СП
dr,gradd
, или, с учётом
=η⋅
η∂
∂
+ξ⋅
ξ∂
∂
= d
r
d
r
dr
21
edGedE ⋅η⋅+⋅ξ⋅=
, получим:
() ()
()
()
() ()
η⋅⋅
ηξ
+
ηξ
−+ξ⋅⋅
ηξ
−
ηξ
=ϕ−ϕ
∫
dGv
,k
a
v
,k
b
dEv
,k
b
v
,k
c
2
2
1
2
П
С
2
2
1
2
СП
. (21)
В частности, если интеграл (21) вычислять вдоль линий тока η = const, а проек-
ции скорости v
1
и v
2
выразить с помощью (1) через ψ(η), то он примет вид
()
()
()
()
()
()
(
)
() ()
()
(
)
∫∫∫
ηξ
ηξ
ηξ
ηξ
ηξ
ηξ
=ξ⋅⋅
ηξ
⋅
η
⋅
=
η⋅
ξ⋅
⋅
ηξ
⋅
=
ηξ
ξ⋅⋅⋅
=ϕ−ϕ
2
1
2
1
2
1
1
2
11
22
1
СП
Cd
G
E
,k
c
L
C
LG
dC
,k
Ec
,k
dvEc
. (22)
Сравнивая теперь (19) и (22), для нижней оценки дебита
Q получим значение
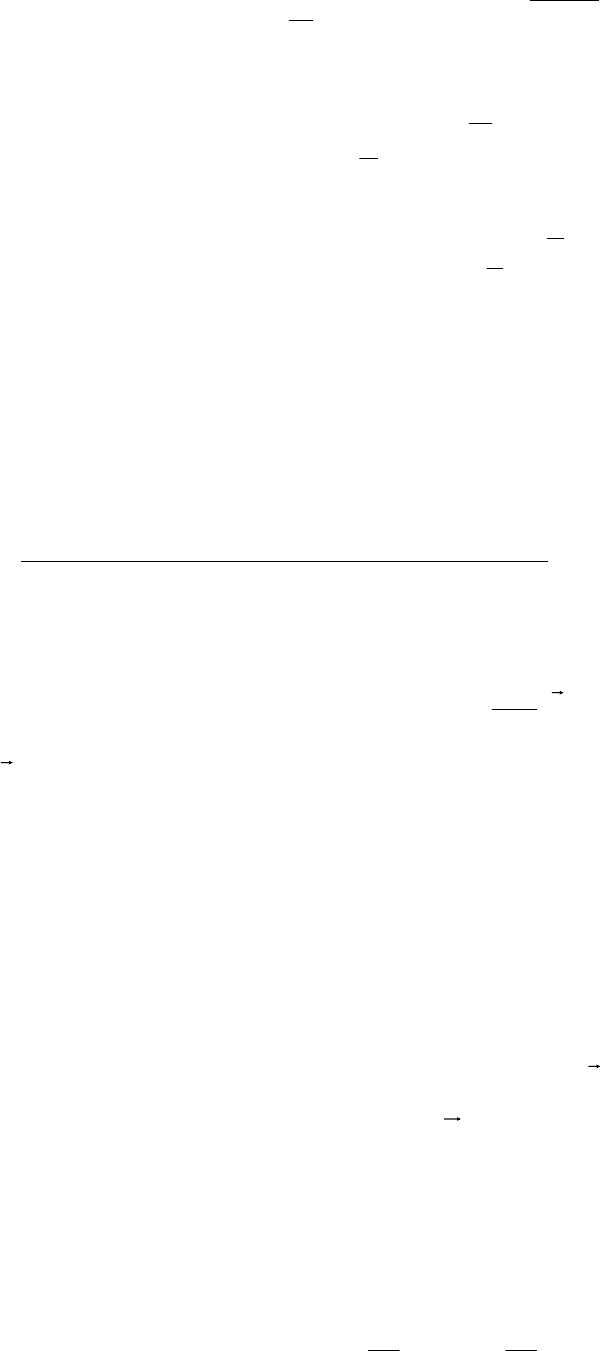
208
()
()
∫
η
η
η
⋅ϕ−ϕ=
0
0
ПС
L
d
Q
. (23)
Таким образом, для Q получена двусторонняя оценка
.QQQ ≤≤
(24)
При выборе аппроксимирующих сеток (ξ,η), правильно отражающих главные осо-
бенности фильтрационного течения, оценки
Q и Q удается сблизить настолько,
что относительная погрешность расчетов по приведенной методике будет состав-
лять 3-5% и менее.
5.3. Расчёт двусторонних оценок дебитов скважин при нелинейных режи-
мах фильтрации
5.3.1. Уравнения движения и граничные условия. Будем исследовать плоскопа-
раллельную фильтрацию несжимаемой жидкости, подчиняющуюся нелинейно-
му закону Дарси [108, 249]
v
v
)v(f
Pgrad ⋅−= (1)
где
−v скорость фильтрации, P - приведённое давление, f(v) - некоторая функ-
ция, характеризующая конкретный вид закона (1) и определяемая эксперимен-
тально. В данном параграфе рассматриваются степенные законы
α
⋅= vB)v(f (2)
где B и α– положительные постоянные. В частности, при α = 1 будем иметь ли-
нейный закон Дарси, а при α = 2 важный для практики закон
А.А. Краснопольского. Поле скоростей фильтрации
v , кроме (1), должно удов-
летворять уравнению неразрывности
0vdiv = , которое позволяет ввести в рас-
смотрение функцию тока течения ψ. Проекции скорости фильтрации в декарто-
вых координатах x,y через ψ будут, как известно [85, 86, 87], вычисляться по
формулам
x
v,
y
v
yx
∂
ψ
∂
−=
∂
ψ
∂
= . (3)
209
С другой стороны, из нелинейного уравнения Дарси (1) со степенными закона-
ми (2) для
yx
vиv получаем:
yv
1
v;
xv
1
v
1
y
1
x
∂
ϕ
∂
⋅=
∂
ϕ
∂
⋅=
−α−α
(4)
где через ϕ обозначено выражение
B
ghp
B
P
ρ
+
−=−=ϕ . (5)
В дальнейшем функцию ϕ будем называть потенциалом скорости фильтрации.
Сравнивая (3) и (4) для функций ϕ и ψ, описывающих нелинейную плоско-
параллельную фильтрацию со степенными законами (2) , получаем систему
xyv
1
;
yxv
1
11
∂
ψ∂
−=
∂
ϕ
∂
⋅
∂
ψ
∂
=
∂
ϕ
∂
⋅
−α−α
. (6)
Из системы уравнений (6) после перекрёстного дифференцирования для функ-
ций ϕ и ψ получаем уравнения
0
y
U
yx
U
x
2
1
2
1
=
∂
ϕ∂
⋅
∂
∂
+
∂
ϕ∂
⋅
∂
∂
α
α−
α
α−
(7)
и
0
y
V
yx
V
x
2
1
2
1
=
∂
ψ∂
⋅
∂
∂
+
∂
ψ∂
⋅
∂
∂
−α−α
, (8)
в которых через U и V обозначены выражения
2
2
22
2
2
22
yx
vV;
yx
vU
∂
ψ∂
+
∂
ψ∂
=ψ∇==
∂
ϕ∂
+
∂
ϕ∂
=ϕ∇==
α
. (9)
Рассмотрим одну из основных задач теории фильтрации – задачу вычисления
удельного дебита скважины. Математическая формулировка этой задачи сво-
дится к отысканию решения нелинейного уравнения (7) в двухсвязной области
D, ограниченной кусочно - гладкими замкнутыми кривыми П (внешняя грани-
ца) и С (внутренняя граница – как правило, окружность с радиусом
0
r , равным
радиусу скважины). На границах D задаются условия
const
П
П
=ϕ=ϕ и const
С
С
=ϕ=ϕ (10)
