Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.


171
нию зависимости дебита от типа конструкции скважинного фильтра. Данные вы-
числительных экспериментов приведены на рис.46. Из него видно, что на практике
целесообразнее использовать фильтры перфорационной конструкции со скважно-
стью 20÷25%. Для данной конструкции (рис.46) характерна высокая пропускная
способность при малой скважности, что позволяет обеспечить фильтру необходи-
мые прочностные качества.
Подчеркнём, что полученные выводы соответствуют результатам произ-
водственных испытаний [30, 81] всех трёх типов фильтров.
4.9 Теорема о подобии фильтрационных полей в грунтах со специальными
законами изменения проницаемости и её применения.
В этом параграфе автором предлагается метод решения краевой задачи
плоскопараллельной напорной фильтрации в целой серии неоднородных грун-
тов со специальными законами изменения проницаемости исходя из решения
точно такой же задачи для какого-то одного грунта из этой серии.
4.9.1 Теорема о подобии фильтрационных полей.
Конкретно, речь пойдёт о реше-
нии краевых задач двух типов. Первая – для двухсвязной области D, на внешней
границе П которой потенциал ϕ скорости фильтрации должен принимать постоян-
ное значение ϕ
П
, а на внутренней границе С- постоянное значение ϕ
С
(рис.47).
Вторая – для односвязной области D (рис.47), у которой на части границы П задано
постоянное значение потенциала ϕ
П
, на другой части границы С потенциал прини-
мает постоянное значение ϕ
С
, а на оставшейся части границы 0
n
=
∂
ϕ∂
. Если прони-
цаемость
()
y,xk
~
грунта в области D изменяется по закону
(
)
(
)
,y,xkky,xk
~
0
= (1)
где
0
k
- постоянная с размерностью проницаемости, ),( yxk - безразмерная пере-
менная, x, y – декартовы координаты в плоскости течения, то потенциал
µ
−=
ϕ
Pk)y,x(
0
и функция тока ),( yx
ψ
, описывающие фильтрацию, будут удов-
летворять системе уравнений [117]

172
xy
)y,x(k;
yx
)y,x(k
∂
ψ
∂
−=
∂
ϕ
∂
∂
ψ
∂
=
∂
ϕ
∂
(2)
Предположим, что решение краевой задачи в D с проницаемостью (1) для системы
уравнений (2) найдено.
Теорема. Если ),( yx
ϕ
и ),( yx
ψ
- решение краевой задачи в D для грунта с прони-
цаемостью (1), то решение
(
)
yx
H
,
ϕ
и
(
)
yx
H
,
ψ
этой же краевой задачи в D для грун-
тов с проницаемостями
)]y,x([f)y,x(kk)]y,x([f)y,x(k
~
)y,x(k
~
0H
ϕ⋅⋅=ϕ⋅= (3)
где
)(
ϕ
f – безразмерная, положительная, ограниченная, с конечным числом точек
разрыва функция находится через ранее найденное решение
ϕ
и
ψ
по формулам:
B)y,x(A)y,x(;
)(f
d
A)y,x(
H
)y,x(
H
+ψ⋅=ψϕ+
τ
τ
⋅=ϕ
Π
ϕ
ϕ
∫
Π
(4)
где
В – произвольная постоянная, а
∫
ϕ
ϕ
Π
Π
τ
τ
ϕ
−
ϕ
=
С
)(f
d
A
C
(5)
В справедливости теоремы для непрерывной функции
)(
ϕ
f убеждаемся непо-
средственной проверкой граничных условий для функции
H
ϕ
и тем, что
H
ϕ
и
H
ψ
удовлетворяют уравнениям напорной фильтрации
[] []
ху
)у,х(f)у,х(к;
ух
)у,х(f)у,х(к
НННН
∂
ψ
∂
−=
∂
ϕ
∂
⋅ϕ⋅
∂
ψ∂
=
∂
ϕ
∂
⋅ϕ⋅
в грунтах с новыми законами изменения проницаемости (3 ). Для разрывной функ-
ции
)(
ϕ
f еще дополнительно проверяем, что (4) на линиях разрыва удовлетворяют
условиям непрерывности давления и нормальной составляющей скорости фильт-
рации.
Следствие. Полный фильтрационный поток Q к границе C области D в
грунтах с проницаемостью (3) через такой же поток
0
Q
в грунте с проницаемо-
стью (1) вычисляется по формуле
0
QAQ
⋅
=
(6)
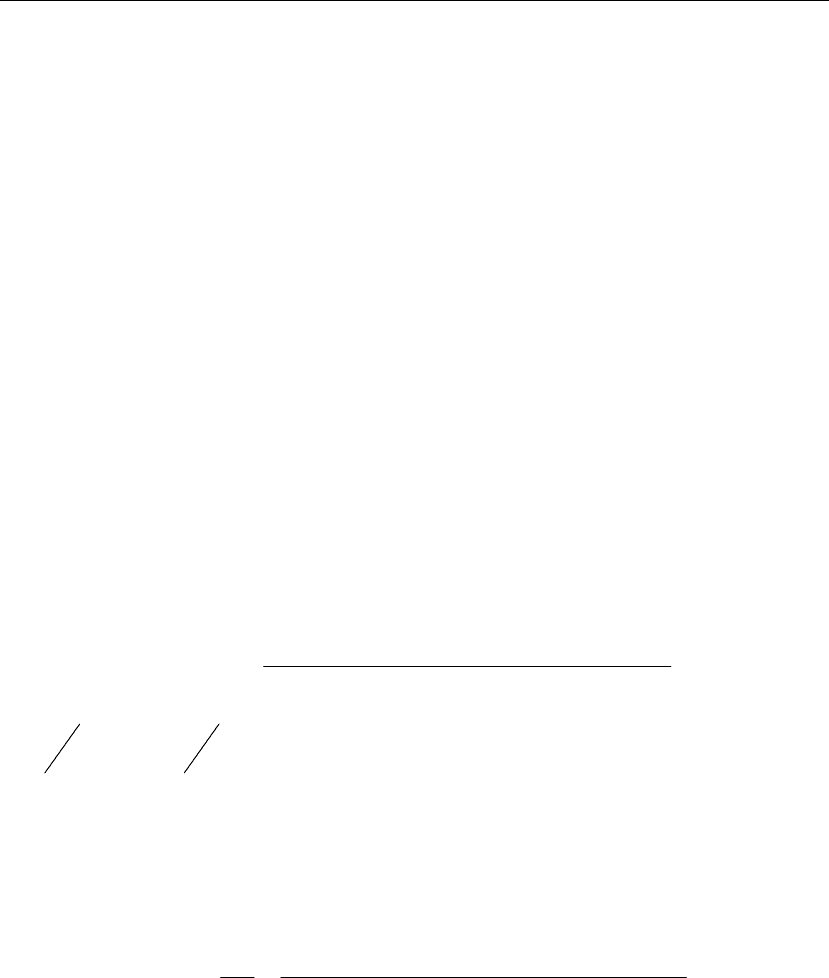
173
Это утверждение вытекает из того, что по свойствам функции тока поток через
границу С области
D равен приращению
),( yx
H
ψ
которое она получает при
движении вдоль
С. В силу (4) приращения функции тока
),( yx
H
ψ
и ),( yx
ψ
бу-
дут связаны друг с другом коэффициентом пропорциональности
А, откуда и
следует утверждение. Приведем конкретные примеры практического примене-
ния теоремы.
4.9.2
. Фильтрация под плоским флютбетом в кусочно – однородном грунте. Исхо-
дя из известного [108, 110] решения задачи о фильтрации под плоским флютбетом
с горизонтальным водоупором в однородном грунте с проницаемостью
0
k на ос-
новании сформулированной теоремы можно получить точные решения такой же
задачи для серии кусочно – однородных сред, когда границами скачков проницае-
мости выступают эквипотенциали течения в однородном грунте
0
k . Пусть, напри-
мер, имеются две кривые скачка проницаемости – эквипотенциали
1
ϕ
и
2
ϕ
, исхо-
дящие из точек (x
1
,0) и (x
2
,0) на основании флютбета ВС )(
21
lxxl
<
<<− (рис.48).
(Все обозначения выбираем соответствующими [108]). Проницаемость грунта сле-
ва от первой эквипотенциали
)(
11
x
ϕ
ϕ
=
равна
0
k , между эквипотенциалями -
1
k , и
справа от второй эквипотенциали
)(
22
x
ϕ
ϕ
=
равна
2
k . Тогда на основании формул
(5) и (6) для фильтрационного расхода жидкости под флютбетом в таком кусочно –
однородном грунте
),,(
210
kkk получим значение
)()()(
Q)(
Q
2CD021201AB1
0ABCD
ϕ−ϕα+ϕ−ϕα+ϕ−ϕ
⋅
ϕ
−
ϕ
= (7)
где
AB
2
0
02
1
0
01
,
k
k
,
k
k
ϕ=α=α
- известное значение потенциала на верхнем бьефе
АВ,
CD
ϕ - заданное значение потенциала на нижнем бьефе CD. Подставляя в (7)
значения потенциала взятые из [108], окончательно для расхода
Q под плоским
флютбетом в кусочно – однородной среде получим:
[][ ]
,
)x(h)x(h)x(h)x(h1
1
Q
Q
21O211O1O
α+−α+−
=
(8)
где
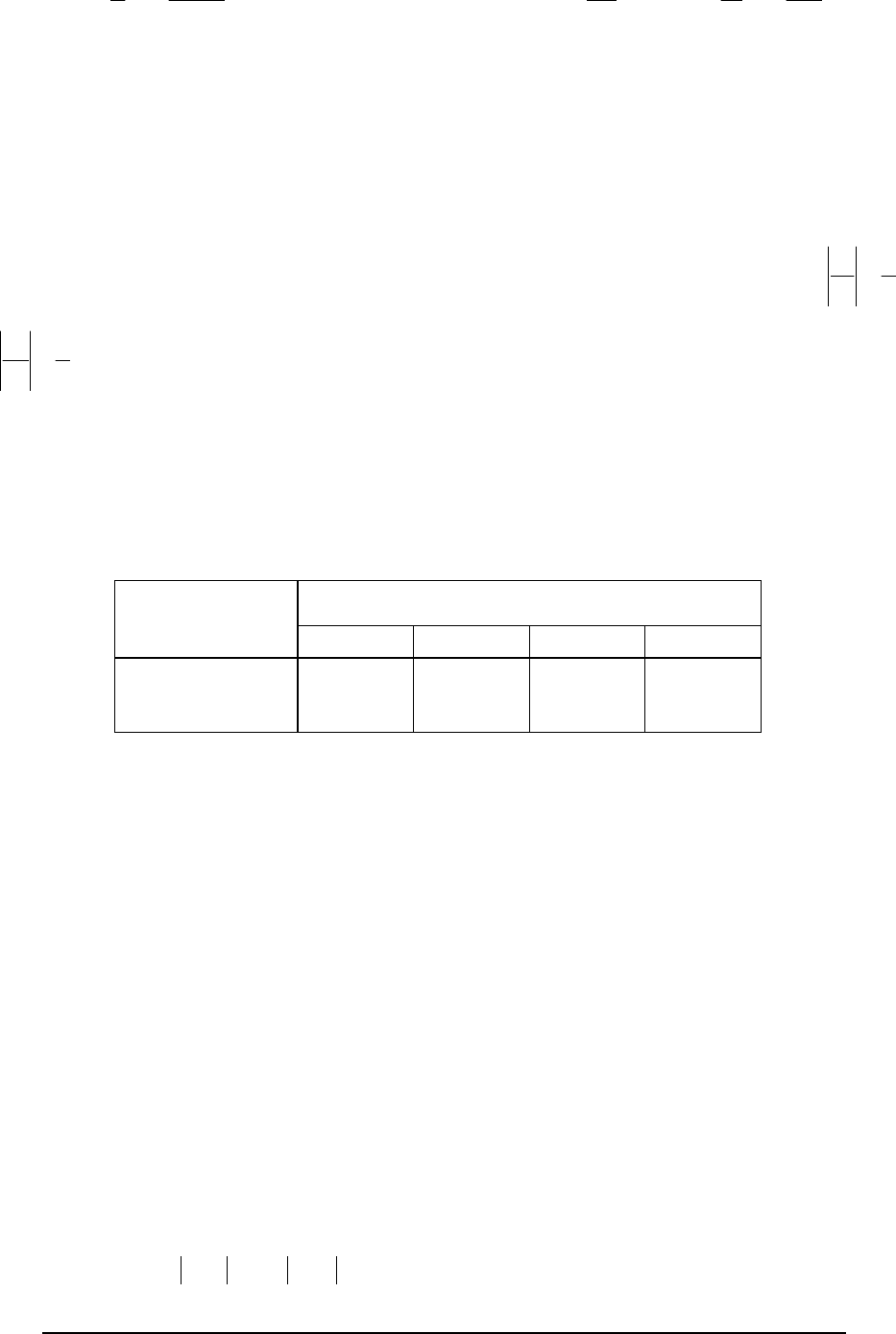
17
4
,
T2
x
th
m
1
t,
T2
thm;2,1i;)m,t(arcsinF
)m(K
1
1
2
1
)x(h
i
iii
π
⋅=
π
==
⋅−=
l
F – эллиптический интеграл 1–го рода, К (m) – полный эллиптический интеграл 1–
го рода,
m – модуль эллиптического интеграла. Формула (8) позволяет выяснить
влияние низкопроницаемой засыпки (
0201
, kkkk
=
<
) сделанной под основанием
флютбета, на полный фильтрационный расход. В частности, если под флютбетом
был вырыт до водоупора котлован с границами
)(
1
x
ϕ
и )(
2
x
ϕ
, которые при
2
1
1
<
l
x
и
2
1
2
<
l
x
близки к вертикальным прямым, и затрамбован низкопроницаемым грун-
том, то расход Q/Q
0
для случая
0201
,5,0 kkkk
=
=
будет таким, как показано в табли-
це 4.3.
Таблица 4.3.
Влияние скачка проницаемости под флютбетом на фильтрационный поток
Tl /
x
2
/l= -x
1
/l
0,25 0,50 1,00 1,50
0,6
0,4
0,2
0,7075
0,7906
0,8852
0,7025
0,7858
0,8819
0,6891
0,7728
0,8730
0,6771
0,7611
0,8649
Отметим, что для вертикальных прямолинейных границ скачка проницаемости эту
же задачу можно решить с помощью модифицированного автором [146] прибли-
жённого метода фрагментов Н.Н. Павловского, когда на границах скачка прони-
цаемости задаётся эпюра нормальной составляющей скорости фильтрации. В чи-
словом выражении по отношению к данным таблицы 4.3 получаются незначитель-
ные изменения (при
5,0/ =Tl в пределах от 2,7% до 8,9%, а при 1/ ≥Tl в пределах
от 0,15% до 2,7% ), а расчетная часть задачи по сравнению с формулой (8) заметно
усложняется. Это показывает, что формула (8), которая точна для криволинейных
границ
)(
1
x
ϕ
и )(
2
x
ϕ
скачка проницаемости, дает в тоже время простой и надеж-
ный способ для приближенного расчета фильтрационных расходов под плоским
флютбетом с вертикальными прямолинейными границами скачка проницаемости
(при условии, что
lxиlx //
21
не более 0,5, а Tl / не менее 0,5 ).
4.9.3. Фильтрация к скважинам с кусочно – однородной призабойной зоной

175
(I–ый способ расчета). Ещё одна область применения сформулированной тео-
ремы - расчёты дебитов скважин со скачком проницаемости в ПЗС. При строи-
тельстве артезианских скважин с целью улучшения их эксплуатационных
свойств вокруг фильтра часто делается гравийная обсыпка в виде кругового ци-
линдра некоторого радиуса [109]. При сооружении нефтедобывающих скважин
перед началом их эксплуатации призабойную зону часто подвергают кислотной
обработке. В результате проницаемость призабойной зоны скважины оказыва-
ется отличной от проницаемости всего пласта. Названные примеры указывают
на практическую важность исследования влияния скачка проницаемости в кру-
говой призабойной зоне скважины на её дебит.
Предположим, что нам известен комплексный потенциал
)у,х(i)у,х()z(w ψ+ϕ= течения к скважине в двухсвязной области D с проницае-
мостью
0
k Будем моделировать круговую границу С скачка проницаемости
ПЗС замкнутой эквипотенциалью
),(
111
yx
ϕ
ϕ
=
, где ),(
111
yxM - некоторая вы-
бранная на
С точка. Тогда на основании формул (5) и (6) дебит Q
1
скважины, в
призабойной зоне которой проницаемость равна
1
k , будет равен
)()(Q
Q
1C1ОП1
ПC
O
1
ϕ−ϕα+ϕ−ϕ
ϕ
−
ϕ
= , (9)
где
1001
k/k=α . Если на круговой границе С выбрать такие две точки ),(
111
yxM и
),(
222
yxM что окружность С окажется заключенной между двумя замкнутыми
эквипотенциалями
),(
111
yx
ϕ
ϕ
= и ),(
222
yx
ϕ
ϕ
=
, то точное значение дебита
Q/Q
0
скважины со скачком проницаемости в круговой призабойной зоне будет
заключено между Q
1
/Q
0
и Q
2
/Q
0
(тоже вычисляемого по формуле (9) с заменой
1
ϕ
на
2
ϕ
). Поэтому за искомое значение дебита скважины с круговой призабой-
ной зоной примем среднее арифметическое
.
2
0
21
0
Q
QQ
Q
Q
+
= (10)
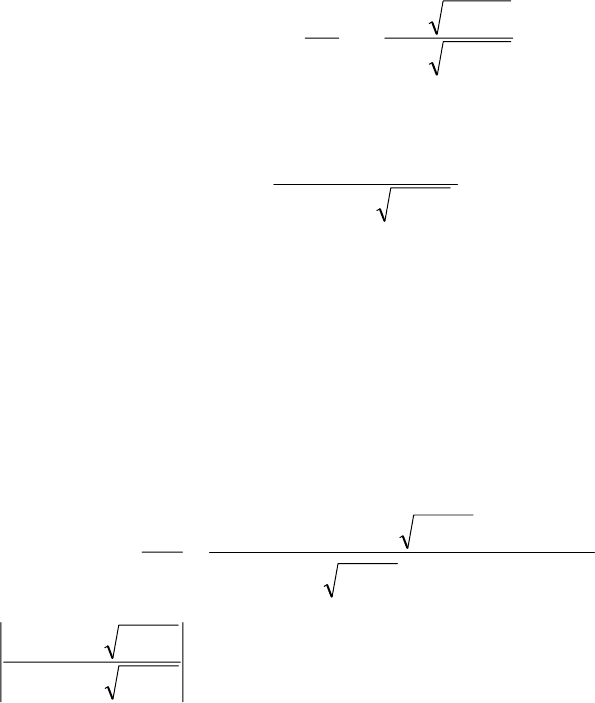
При этом погрешность приближенного значения дебита, рассчитанного по
формулам (9) и (10), не превзойдет величины
)/(100)(%
1212
QQQQ
+
⋅
−
=
δ
(11)
176
Приведем два конкретных примера применения описанного метода.
Пример №1. Скважина с круговой ПЗС и прямолинейной границей области
питания (рис.49).
Пусть центр круговой скважины с радиусом
0
r находится в
точке 0,
0
>= lilz . Границей П (контур питания) двухсвязной области фильтра-
ции
D служит ось абсцисс. Точное решение задачи о фильтрации к такой сква-
жине дается комплексным потенциалом [48]
A
riz
riz
ln
2
Q
)r(w
2
O
2
2
O
2
O
+
−+
−−
⋅
π
−=
l
l
, (12)
а её дебит Q
0
в однородном грунте
0
k равен
(
)
,
1ln
)рр(к2
Q
2
OO
СПО
O
−+⋅µ
−
π
=
ll
(13)
где
)(
СП
рр − - разность приведённых давлений на контуре питания и на стволе
скважины,
00
r/ll = . Обозначим радиус круговой призабойной зоны с проницае-
мостью k
1
через r
1
В качестве точек М
1
и М
2
выберем точки (0, l − r
1
) и (0, l+r
1
).
Выделяя в (12) действительную часть, вычисляя затем
)M(и)M(
21
ϕϕ и под-
ставляя
1
ϕ
и
2
ϕ
в (9), получим:
(
)
(
)
,
)ln()1(1ln
1ln
Q
Q
2,11O
2
OO1O
2
OO
O
2,1
β−α+−+α
−+
=
ll
ll
(14)
где
O1O1
2
OO1O
2
OO1O
2,1
r/rr,
1r
1r
=
−+±
−−±
=β
ll
ll
.Теперь с помощью формул (10) и (14)
можно рассчитать влияние скачка проницаемости в круговой призабойной зоне
на дебит скважины.
Пример №2. Скважина с круговой ПЗС и с эксцентричной к ней круговой
границей области питания (рис.50)
. Пусть контуром питания (границей П
двухсвязной области фильтрации D) служит окружность радиуса R с центром в
начале координат, центр круговой скважины радиуса
0
r находится в точке
Rr;R0;z
OO
<+<<= lll . Точное решение задачи о фильтрации к такой скважи-
не дается комплексным потенциалом [48]

177
A
xz
xz
ln
2
Q
)z(w
2
1
O
+
−
−
⋅
π
−=
, (15)
а её дебит Q
0
в однородном грунте
0
k равен
()
OO
2
O
2
O
2
2
O
2
OO
O
O
2
O
2
O
O2
O
2
OO
O
O
2
O
2
O
O1
O
1
O
O
2
O
2
O
СПO
O
r;R41RD;
2
D1R
x
r
x
;rRR;
2
D1R
x
r
x
где;
R2
D1R
ln
)рр(k2
Q
llll
l
l
l
l
l
=−−+=
+−+
==
=
−−+
==
+−+
⋅µ
−π
=
.
Как и выше, обозначим радиус круговой призабойной зоны с проницаемостью
k
1
через r
1
. В качестве точек М
1
и М
2
выберем точки )0,(
1
rl − и )0,(
1
rl + . Далее
выделим в (15) действительную часть, вычислим
)(
1
M
ϕ
и )(
2
M
ϕ
и подставим в
(9). В результате получим, что
)ln()1(
R2
D1R
ln
R2
D1R
ln
Q
Q
2,11O
O
O
2
O
2
O
1O
O
O
2
O
2
O
O
2,1
β⋅−α+
+−+
α
+−+
=
l
l
(16)
где
O1O1
O2O1O
O1O1O
OO
O
2
O
2
O
2,1
r/rr;
xr
xr
R2
D1R
=
−±
−±
⋅
+−+
=β
l
l
l
l
. Формулы (10) и (16) позво-
ляют рассчитать влияние скачка проницаемости в круговой призабойной зоне
на дебит данной скважины.
Погрешности расчётов дебитов скважин с кусочно – однородной приза-
бойной зоной, которые выполняются по формулам (9), (10), а в примерах№1 и
№2 - по формулам (10), (14) и (10), (16), определяются по формуле (11). Однако
формула (11) дает, как было выявлено в числовых экспериментах, часто завы-
шенное значение погрешности. Поэтому для получения более точной оценки
погрешности результата, получаемого на основании (9) и (10), полезно прово-
дить сопоставления с расчётами дебитов по какому – то другому способу. В
связи с этим наряду с вышеизложенным предлагается ещё один способ для рас-
чета дебита скважин со скачком проницаемости в круговой ПЗС.
4.9.4. Фильтрация к скважинам с кусочно – однородной призабойной зоной.

178
(2–ой способ расчета). Математическая формулировка задачи о дебите скважи-
ны с центральной круговой границей
С скачка проницаемости сводится к оты-
сканию комплексных потенциалов течения
)y,x(i)y,x()z(w
111
ψ
+ϕ= и
)y,x(i)y,x()z(w
222
ψ
+ϕ= переменной iyxz
+
=
действительные части которых
удовлетворяли бы условиям
С22
21
1
2
О
1
П11
;
C
n
C
n
;
С
к
С
к
;
П
ϕ=
γ
ϕ
∂
ϕ∂
=
∂
ϕ∂ϕ
=
ϕ
ϕ=ϕ
. (17)
(Через γ обозначен круговой контур скважины радиуса
0
r ). Точное решение
краевой задачи (17) для аналитических функций
)z(w
1
и )z(w
2
находится просто
только для круговой области
D с центральным расположением скважины. Для
других областей
D отыскание точного решения краевой задачи (17) вызывает
значительные трудности. В этом параграфе автор предлагает новый метод при-
ближенного решения краевой задачи (17). Идея предлагаемого метода основана
на том, что в непосредственной близости к скважине течение жидкости можно
принять за плоскорадиальное. Поэтому в качестве комплексного потенциала
w
2
(z) выберем функцию
A)zzln(
2
Q
)z(w
O
2
2
+−⋅
π
−= , (18)
где z
0
- комплексная координата скважины, Q
2
–её дебит, А - некоторая пока не-
известная действительная постоянная. Действительная часть
2
ϕ
потенциала (18)
на круговой границе
С скачка проницаемости будет постоянной величиной.
Поэтому на основании второго из граничных условий (17)
1
ϕ
тоже будет посто-
янной на
С. Комплексный потенциал )z(w
1
, действительная часть которого
должна принимать постоянные значения на границах
П и С двухсвязной облас-
ти (получаемой из
D удалением круга с границей С), может быть найден с по-
мощью конформного отображения этой двухсвязной области на некоторое кру-
говое кольцо (рис.51). С гидродинамической точки зрения такая задача равно-
сильна отысканию точного комплексного потенциала течения к круговой сква-
жине с границей
С. В общем случае решение этой задачи имеет вид [48, 108]

179
()
[]
Bztln
2
Q
)z(w
1
1
+⋅
π
−= (19)
где
t=t(z) – функция, реализующая конформное отображение названной двух-
связной области на круговое кольцо в плоскости
t, а Q
1
и В - некоторые пока
неизвестные постоянные. Если функция
t=t(z) будет найдена, то далее останет-
ся определить значения 4-х произвольных постоянных:
А, Q
1
, Q
2
и В. Эти по-
стоянные найдем с помощью граничных условий (17). Третье из граничных ус-
ловий (17) выражает равенство нормальных составляющих
nn
vv
21
= скорости
фильтрации в каждой точке на окружности
С. Это единственное из перечис-
ленных в (17) граничное условие, которое в предлагаемом методе выполняется
приближенно. А именно, требование равенства
nn
vv
21
=
в каждой точке С заме-
ним на равенство потоков жидкости через контур
С. Поскольку поток жидкости
через контур
С для течения с потенциалом )(
1
zw равен Q
1
, а течения с потен-
циалом
)(
2
zw
равен Q
2
, то для равенства потоков потребуем, чтобы
QQQ
21
=
=
(20)
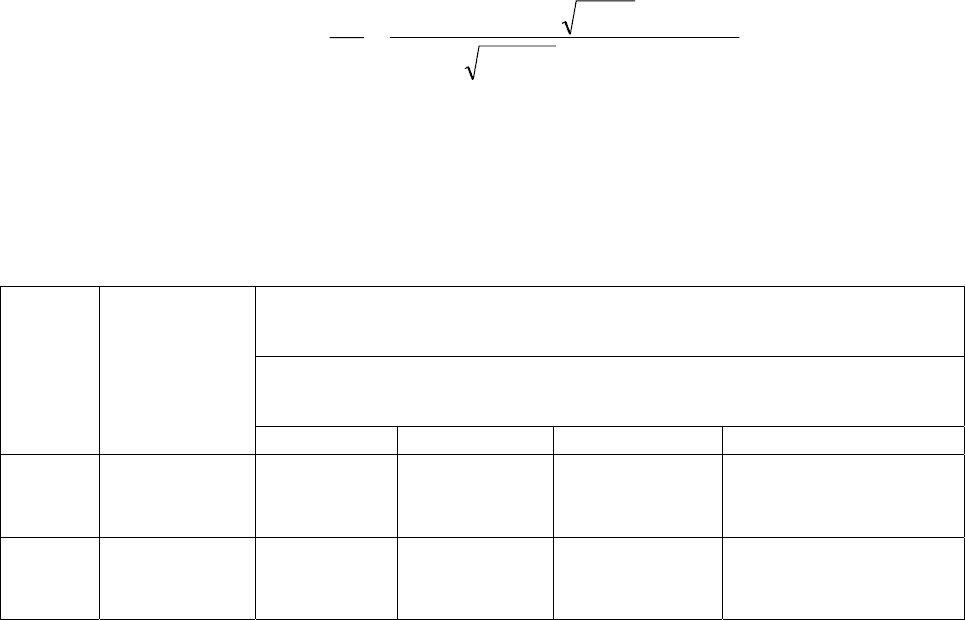
Для определения теперь уже трех постоянных
А, Q и В воспользуемся первым,
вторым и четвертым условиями в (17). После выделения в (18) и (19) действи-
тельных частей, условия (17) с учетом (20) дадут три линейных уравнения для
неизвестных
Q, А и В. Решая эти уравнения, для дебита Q получим:
⋅+⋅µ
−
π
=
O
1
O
C
П
1
СП1O
r
r
lnk
)z(t
)z(t
lnк
)рр(kk2
Q
(21)
где
Π
z и
C
z - комплексные координаты точек контура питания П и окружности
С. Таким образом, если функция t=t(z), осуществляющая конформное отобра-
жение области
D с выброшенным кругом на круговое кольцо в плоскости t бу-
дет найдена, то задача окажется решенной.
Подчеркнем, что если в формуле (21) радиус
01
rr
=
т. е. скачок проницае-
мости в призабойной зоне отсутствует, то (21) даст точное значение дебита Q
0
круговой скважины. Если же в (21) выбрать
01
kk
=
, а
01
rr ≠
то получим при-
ближенное значение для дебита круговой скважины. Погрешность в расчете
Q
180
по формуле (21) при
01
kk = и
01
rr
≠
появится из – за введения в сетку течения
искусственной эквипотенциали радиуса
1
r . Поэтому отклонения
0
/ QQ от 1 при
01
kk = и
01
rr ≠ косвенным образом позволяют оценить погрешности в расчетах
Q по второму предложенному методу. Отметим, что в рассмотренных далее
примерах эти отклонения составляли доли процента, если отношение
1
r к ха-
рактерному размеру области фильтрации было менее 0,1.
Теперь применим новый подход к решению тех же примеров.
Пример I. Скважина с круговой ПЗС и с прямолинейной границей области
питания (рис.49).
Конформное отображение верхней полуплоскости с выбро-
шенным кругом на кольцо известно [78, 123]. Поэтому формула (21) после под-
становки в нее известной функции t(z) и алгебраических преобразований при-
мет вид:
(
)
(
)
O11O
2
O1
2
OO
2
OO
O
rln)1(rln
1ln
Q
Q
⋅−α+−+
−+
=
ll
ll
. (22)
Влияние скачка проницаемости на дебит скважины, рассчитанное по формуле
(22), приведено в таблице 4.4.
Таблица 4.4.
Влияние скачка проницаемости в круговой призабойной зоне на дебит скважины
(рассчитаны отношения Q/Q
0
по формуле (22))
Пример №1
l
0
r
10
k
1
/ k
0
50 100 200 1000
5
0,5
2,0
20,0
0,74
1,21
1,50
0,77
1,18
1,41
0,79
1,16
1,34
0,83
1,12
1,25
10
0,5
2,0
20,0
0,67
1,34
1,91
0,70
1,28
1,70
0,72
1,24
1,58
0,77
1,18
1,40
Пример 2. Скважина с круговой неоднородностью и с эксцентричной к ней кру-
говой границей области питания (рис.50).
Функция t(z), реализующая кон-
формное отображение большого круга с выброшенным внутренним кружком на
кольцо приводится в [78, 123]. Подставляя t(z) в (21) для дебита скважины в ус-
ловиях 2-го примера получим выражение
