Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.


141
⋅⋅µ
⋅−⋅
+=
π
⋅π+
=+
c
2
c
П1
2
c
2
c
r
R
lnr
dz))z(PP(k2
)z(u
r
)z(ur)z(dq
)dzz(u
. (7)
С другой стороны, величина скорости u(z+dz) связана с распределением давле-
ния в стволе скважины по закону (2). Поэтому должно быть выполнено равен-
ство
)]dzz(u[f
dz
)dzz(dP
+−=
+
. (8)
Вычитая из (8) соответствующие части равенства (2), получим
{}
)]z(u[f)]dzz(u[f
dz
)z(dP
dz
)dzz(dP
−+−=−
+
. (9)
Если теперь к обеим частям последнего выражения применить известную в ма-
тематическом анализе теорему Лагранжа [61, 213] и перейти к пределу при
dz→0, то из (9) с учетом равенства (7) получим:
)]z(u['f
r
R
lnr
)]z(PP[k2
dz
)z(Pd
c
2
c
П1
2
2
⋅
⋅⋅µ
−⋅
−=
. (10)
(Штрих ' обозначает дифференцирование f по u). Уравнение (10) содержит две
неизвестных функции: приведенное давление внутри ствола скважины P(z) и
скорость потока жидкости в стволе скважины u(z). Поэтому для решения задачи
еще нужно определить уравнение для u(z). Чтобы найти u(z) подсчитаем, поль-
зуясь формулой (6), весь приток жидкости к скважине на участке [0, z]:
∫∫
−⋅
⋅µ
π
==
z
0
П
c
1
z
0
dz))z(PP(
r
R
ln
k2
)z(dq)z(q
. (11)
Таким образом, через сечение z скважины должен проходить за единицу време-
ни поток жидкости q(z), но тогда средняя скорость течения жидкости u(z) будет
равна
2
c
r
)z(q
π
, т.е.
∫
−⋅
⋅⋅µ
=
z
0
П
c
2
c
1
dz))z(PP(
r
R
lnr
k2
)z(u
. (12)

142
Подставив (12) в (10), относительно неизвестной функции распределения дав-
ления Р(z) в стволе скважины получим одно интегро-дифференциальное урав-
нение. Для решения этого уравнения нужно еще дополнительно задать краевые
условия на границах z=0 и z=b активного участка скважины. В сечении на
кровле пласта z=b (рис.33) должно быть задано давление в скважине, поэтому
Р|
z=b
=Р
С
. (13)
В сечении z=0 (на подошве пласта) нормальная составляющая скорости потока
u(0)=0, а следовательно,
0)0(f)]0(u[f
dz
dP
0z
=−=−=
=
. Поэтому
0
dz
dP
0z
=
=
. (14)
Таким образом, интегро-дифференциальное уравнение, получающееся при под-
становке (12) в (10), должно интегрироваться совместно с краевыми условиями
(13), (14).
После того, как функция P(z) будет найдена, дебит Q скважины можно вы-
числить по формуле (11) при z=b:
∫
−⋅
⋅µ
π
=
b
0
П
c
1
dz))z(PP(
r
R
ln
k2
Q
. (15)
Формула (15) представляет собой уточнение классической формулы Дюпюи для
дебита Q
0
совершенной центральной скважины
⋅µ
⋅
−
⋅
π
=
c
cП1
0
r
R
ln
b)PP(k2
Q
. (16)
Отношение Q/Q
0
, равное
∫
−⋅
−⋅
=
b
0
П
cП0
dz))z(PP(
)PP(b
1
Q
Q
, (17)
будет характеризовать величину погрешности, если для расчета дебита скважины
с гравийным фильтром использовать формулу Дюпюи (16).

143
(Б) Вывод дифференциального уравнения для скорости течения в фильтре
скважины
Более простой по сравнению с (10), (12) и удачно его дополняющий спо-
соб расчета гидротехнических характеристик скважины можно получить, если
за основу взять распределение в её фильтре скорости течения u(z). Поэтому в
дополнение к (10), (12) выведем ещё дифференциальное уравнение для скоро-
сти фильтрации u(z). Прежде всего заметим, что для производной
dz
du
из форму-
лы (7) с учетом (16) получается значение
CП
П
2
c
0
PP
)z(PP
br
Q
dz
du
−
−
⋅
⋅⋅π
= . (18)
Дифференцируя обе части (18) по z и учитывая формулы (2) и (16), для скоро-
сти фильтрации u(z) получим уравнение
)u(f
)PP(br
Q
dz
ud
CП
2
c
0
2
2
⋅
−⋅⋅⋅π
= . (19)
Дифференциальное уравнение (19) должно интегрироваться совместно с краевыми
условиями
0u
0z
=
=
и
br
Q
dz
du
2
c
0
bz
⋅⋅π
=
=
. (20)
Первое из условий (20) означает, что нормальная составляющая скорости пото-
ка на подошве пласта отсутствует, а второе условие сразу следует из (18) при
z=b. Для интегрирования уравнения (19) применяем известный прием – вводим
подстановку
)u(G
dz
du
= , (21)
с помощью которой из (19) находим, что
1
u
0
CП
2
c
0
2
Cdu)u(f
)PP(br
Q2
)u(G +⋅
−⋅⋅⋅π
=
∫
, (22)
где С
1
– произвольная постоянная. Для определения С
1
рассмотрим равенство
(22) при z=b. Обозначим неизвестную скорость фильтрации при z=b через u
*
,
т.е.
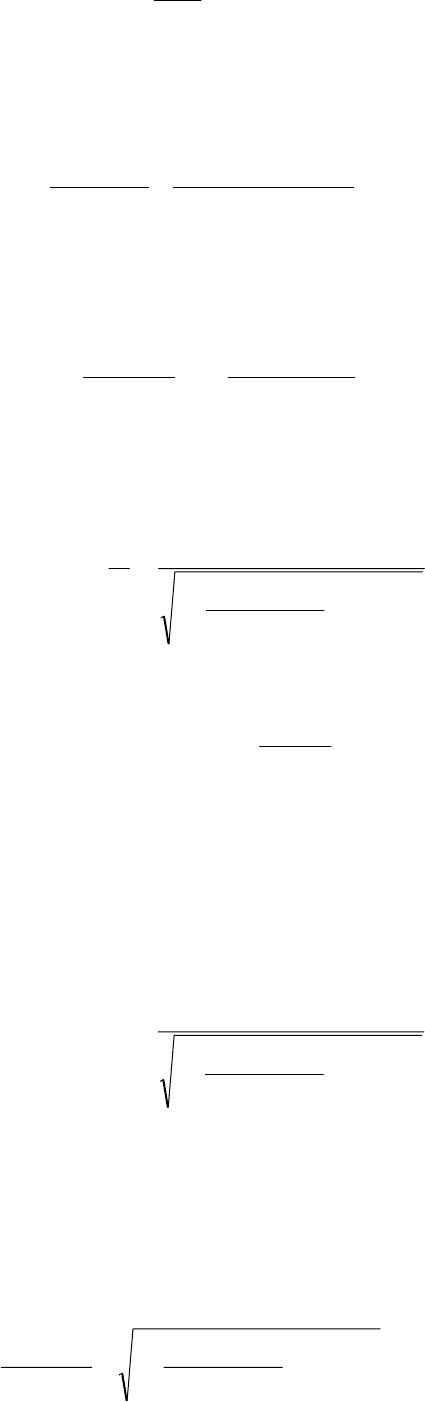
14
4
)b(u
r
Q
u
2
c
*
=
⋅π
= , (23)
где Q – дебит скважины с гравийным фильтром. Тогда с учетом второго крае-
вого условия (20) для С
1
из (22) получим значение
∫
⋅
−⋅⋅⋅π
−
⋅⋅π
=
*
u
0
CП
2
c
0
24
c
2
2
0
1
du)u(f
)PP(br
Q2
br
Q
C
. (24)
Подставляя теперь (24) в (22) для вспомогательной функции G(u) найдем выра-
жение
⋅
−⋅
⋅⋅π
−⋅
⋅⋅π
=
∫
*
u
0
CП0
2
c
24
c
2
2
0
2
du)u(f
)PP(Q
br2
1
br
Q
)u(G . (25)
Теперь, когда G(u) стала известной, с помощью (21) и первого условия (20) оп-
ределим распределение скорости u(z):
,
du)u(f
)PP(A
2
1
du
A
1
z
u
0
u
u
CП
*
∫
∫
⋅
−⋅
−
⋅=
(26)
где введено обозначение
br
Q
A
2
c
0
⋅⋅π
=
. (27)
Для того, чтобы можно было применить (26) к расчету скорости u(z) ос-
тается определить оставшуюся неизвестной постоянную u
*
. Уравнение для u
*
получим с помощью (26) при значении z=b. Учитывая (23), приходим к сле-
дующему уравнению для u
*
:
∫
∫
⋅
−⋅
−
=⋅
*
*
u
0
u
u
CП
du)u(f
)PP(A
2
1
du
bA
. (28)
Из уравнения (28) вычислим u
*
, а стало быть и дебит Q по формуле (23). Затем
по формуле (26) можно будет найти распределение скорости u(z) в фильтре
скважины. Наконец, с помощью формул (18), (21) и (25) найдем распределение
давления в стволе скважины по ее высоте:
∫
⋅
−⋅
−=
−
−
*
u
u
CПCП
П
du)u(f
)PP(A
2
1
PP
)z(PP
. (29)
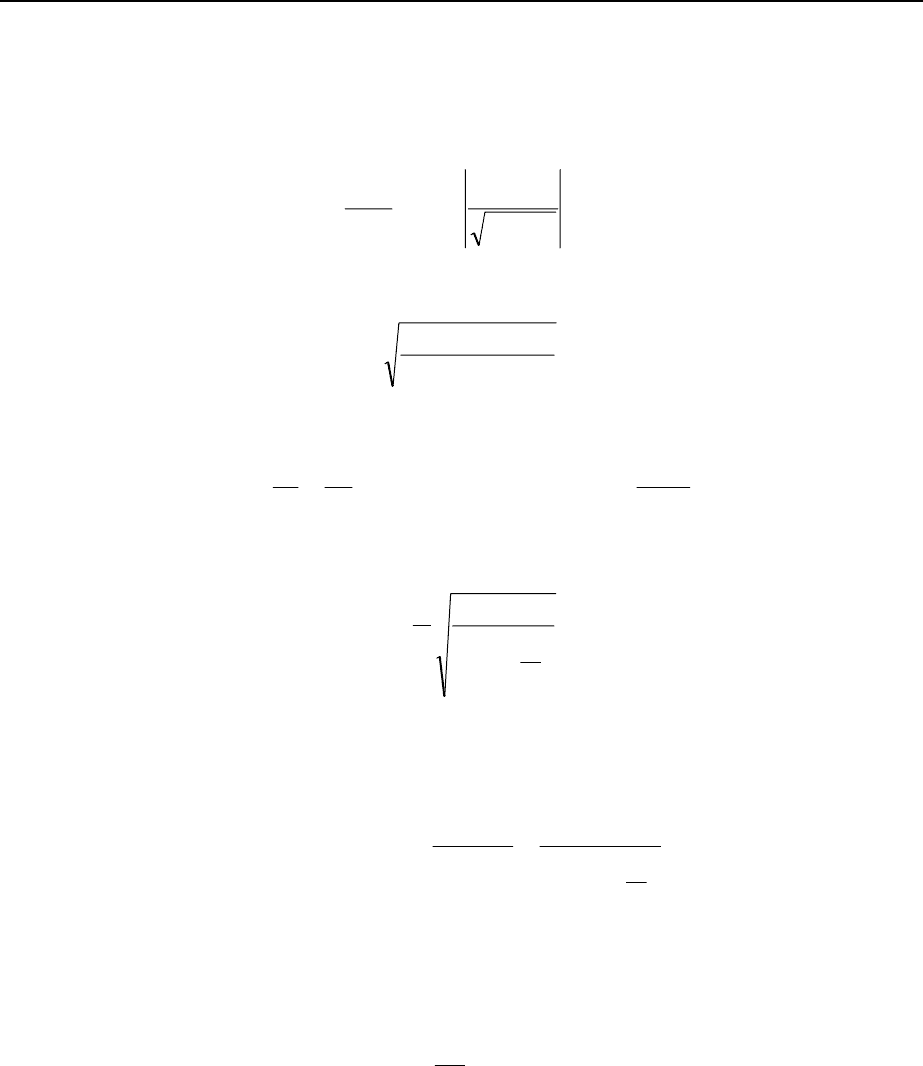
145
Таким образом, задача о расчете гидротехнических характеристик сква-
жины с гравийным фильтром оказалось полностью решенной.
4.3.3. Анализ работы гравийного фильтра при линейном режиме фильтрации
Рассмотрим случай, когда в скважине с гравийным фильтром обеспечива-
ется линейный режим фильтрации. В этом случае функция f(u) задается форму-
лой (3), а уравнение (28) после вычисления интегралов примет вид:
2
*
2
*
2
c
0
uv
~
v
~
u
lnv
~
r
Q
−
+
⋅=
⋅π
, (30)
где введено обозначение
µ
−⋅⋅
=
)PP(kA
v
~
CП2
. (31)
Решая уравнение (30) для u
*
найдем значение
)x(h
r
b2
v
u
c0
*
⋅= где
x
)x(th
)x(h =
. (32)
В формуле (32) через х обозначена вспомогательная безразмерная переменная
⋅
=
c
2
1
c
r
R
lnk
k2
r
b
x
, (33)
а через v
0
– масштабная постоянная с размерностью скорости фильтрации, вы-
числяемая с помощью формулы Дюпюи (16):
⋅⋅µ
−
⋅
=
⋅⋅π
=
c
c
CП1
c
0
0
r
R
lnr
)PP(k
br2
Q
v
. (34)
Теперь, зная u
*
, по формуле (23) находим дебит Q скважины с гравийным
фильтром
)x(h
Q
Q
0
= . (35)

146
Распределение скорости фильтрации в скважине с гравийным фильтром
по её высоте находим по формуле (26). После вычисления интегралов получим,
что
)x(chx
b
z
xsh
r
b2
v
)z(u
c0
⋅
⋅
⋅=
. (36)
Распределение по высоте приведенного давления в скважине с гравийным
фильтром находим по формуле (29). В результате расчетов получили, что
)x(ch
b
z
xch
P
P
11
P
)z(P
П
C
П
⋅
⋅
−−=
. (37)
Важной количественной характеристикой работы фильтра является рас-
пределение скорости фильтрации
⋅⋅µ
−
⋅
=
⋅⋅π
=
c
c
П1
c
r
R
lnr
))z(PР(k
dzr2
)z(dq
)z(v
(38)
(формула (6) и рис.34) флюида по высоте внешней поверхности ствола скважины.
После подстановки в (38) формулы (37) для v(z) получаем выражение
)x(ch
b
z
xch
v
)z(v
0
⋅
=
. (39)
Заметим, что формулы (35), (36) и (37) в случае линейного в стволе скважины с
гравийным фильтром закона Дарси могут быть получены иначе. А именно, с
помощью уравнений (10) и (12), которые при линейной фильтрации становятся
независимыми друг от друга. Вследствие этого уравнение (10) будет обыкно-
венным дифференциальным уравнением, не вызывающем затруднений с его
интегрированием.
Формулы (36) и (39) применены для вычисления фильтрационных чисел
Рейнольдса в 1 и 2 областях (рис.33) с целью определения условий, обеспечи-
вающих скважине с гравийным фильтром линейный режим фильтрации. Число
Рейнольдса Re, как известно, вычисляется по формуле [16, 112]

147
f
kv
Re ⋅
ν
⋅
= , (40)
где v – скорость фильтрации; k – проницаемость среды;
ρ
µ
=ν
- кинематиче-
ский коэффициент вязкости флюида; f – множитель, зависящий, главным обра-
зом, от пористости m среды, а также от формы и шероховатости стенок поро-
вых каналов и их извилистости. Разные авторы для f дают разные формулы.
Так, Щелкачев В.Н., Миллионщиков М.Д., Котяхов Ф.И. и Требин Г.Ф. для f
предлагают соответственно формулы [16, 112, 229]
3,2
Щ
m
10
f
= ;
5,1
М
m
1
f
= ;
5,1
КТ
m
24
f
= . (41)
Для того, чтобы в области фильтрации был справедлив линейный закон Дарси
требуется выполнение неравенства Re<Re
кр
. Перечисленные авторы для опре-
деления верхней границы существования закона Дарси указывают не только
разные формулы (41) для f, но и разные значения критического числа Re
кр
. По
Щелкачеву В.Н. Re
кр
=1÷12; по Миллионщикову М.Д. Re
кр
=0.022÷0.6; по Котя-
хову Ф.И. и Требину Г.Ф. Re
кр
=0.2÷3.4.
Подставляя в (40) скорость фильтрации v(z) из (39), для чисел Рейнольдса
Re
1
в 1-ой зоне области фильтрации (рис.33) на внешней поверхности ствола
скважины получаем выражение
()
00
1
v
zv
)x(ch
b
z
xch
Re
Re
=
⋅
=
, (42)
где
1
10
0
f
kv
Re ⋅
ν
⋅
= . (43)
Формула (43) определяет значение числа Рейнольдса Re
0
на внешней поверхно-
сти ствола совершенной центральной скважины, для которой справедлива фор-
мула Дюпюи (16).
Если в (40) подставить скорость фильтрации u(z) из (36), то получим зна-
чения чисел Рейнольдса Re
2
для течения в фильтре скважины ( во 2-ой зоне об-
ласти фильтрации):
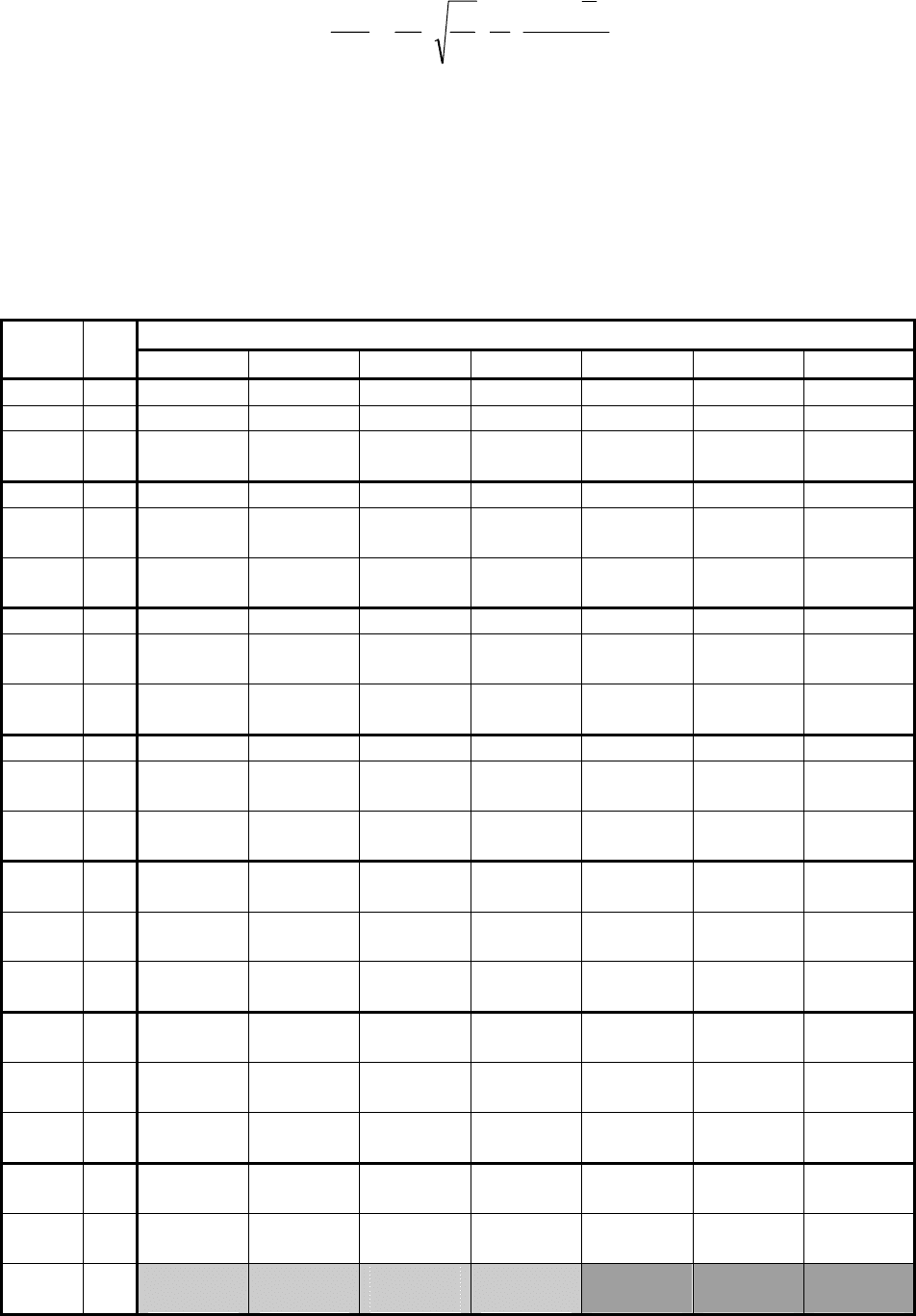
148
)x(chx
b
z
xsh
f
f
k
k
r
b2
Re
Re
1
2
1
2
c0
2
⋅
⋅
⋅⋅⋅=
. (44)
Таблица 4.1. Режимы течения жидкости во внешней окрестности и внутри ствола скважи-
ны с гравийным фильтром при r
скв
= 0,1 м; R / r
скв
= 5000 м; ρ = 850 кг / м
3
; m = 0,2; b / r
скв
=
100; P
п
– P
с
= 10 МПа;
k
1
/ k
2
k
1
, Д
µ,
спз
1,0 0,1 0,01 0,001 0,0001 0,00001 0,000001
0,100 40
0,100 10
0,100 2
++++++++
++
++++++++
++
0,500 40
0,500 10
++++++++
++
++++++++
++
0,500 2
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
0,750 40
0,750 10
++++++++
++
++++++++
++
++++++++
++
0,750 2
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
#########
#
1,000 40
1,000 10
++++++++
++
++++++++
++
++++++++
++
++++++++
++
1,000 2
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
#########
#
#########
#
1,500 40
++++++++
++
1,500 10
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
1,500 2
++++++++
++
++++++++
++
++++++++
++
++++++++
++
#########
#
#########
#
#########
#
2,000 40
++++++++
++
++++++++
++
2,000 10
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
2,000 2
++++++++
++
++++++++
++
++++++++
++
++++++++
++
#########
#
#########
#
#########
#
3,000 40
++++++++
++
++++++++
++
++++++++
++
3,000 10
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
++++++++
++
#########
#
3,000 2
++++++++
++
++++++++
++
++++++++
++
#########
#
#########
#
#########
#
#########
#
Примечания:
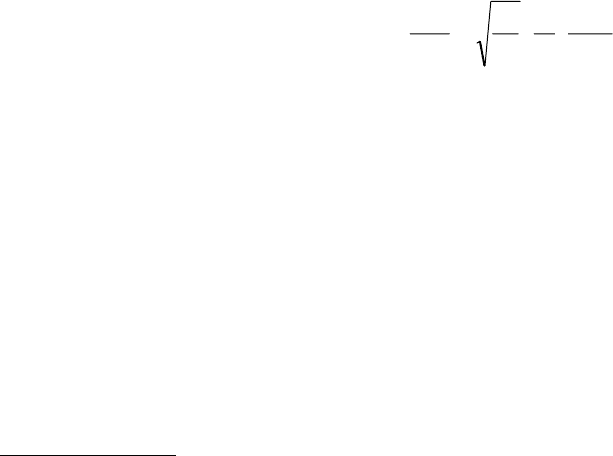
149
1) Пустая ячейка указывает на линейный режим фильтрации по всей длине фильтра скважины; ли-
нейный режим фильтрации вблизи внешней поверхности ствола скважины.
2) Ячейка заполненная символом «+» указывает на переходный режим фильтрации (у подошвы
пласта фильтрация линейная, у кровли – нелинейная).
3) Ячейка заполненная символом «#» указывает на нелинейный режим фильтрации по всей длине
фильтра скважины.
4) Ячейка серого цвета обозначает, что вблизи внешней поверхности ствола скважины переходный
режим фильтрации (от линейной фильтрации у подошвы пласта к нелинейной у его кровли).
5) Ячейка темно-серого цвета обозначает, что вблизи внешней поверхности ствола скважины суще-
ствует нелинейный режим фильтрации по всей длине фильтра скважины.
Сопоставление формул (36) и (44) показывает, что
01
2
1
2
0
2
v
)z(u
f
f
k
k
Re
Re
⋅⋅=
, (45)
т.е. числа Рейнольдса Re
2
течения флюида в гравийном фильтре прямо пропор-
циональны скорости фильтрации u(z) в стволе скважины. Формулы (35)-(39),
(42) и (45) применялись для расчётов дебитов скважин с гравийным фильтром,
для распределений давления и скорости фильтрации по высоте и для выявления
условий существования линейного режима фильтрации. Результаты некоторых
вычислений представлены в таблице 4.1 и на рис.35-39. По результатам вычис-
лений можно сделать следующие выводы.
4.3.4. Выводы:
1). Если безразмерный параметр х, определяемый по формуле (21), принимает зна-
чение х≤0.5, то тогда:
- приведенное давление вдоль ствола скважины можно считать постоянным,
равным Р
с
;
- дебит центральной скважины можно вычислять по классической формуле Дю-
пюи;
- скорость фильтрации имеет равномерное распределение по всей длине ствола
скважины.
2). Если х>0.5, то приток флюида в скважину происходит неравномерно: у подош-
вы пласта скорости фильтрации ничтожно малы (застойная зона), а при приближе-
нии к кровле пласта скорости резко возрастают. Последнее может приводить к вы-
мыву частиц породы пласта возле кровли в скважину. Приведенное давление мо-
жет вдоль ствола изменяться в очень широких пределах, включая крайние пределы

150
изменения от Р
П
до Р
С
. Расчет дебита по формуле Дюпюи (16) в этих случаях при-
водит к сильно завышенным значениям.
3). Из таблицы 4.1 вытекает, что в ПЗС и в гравийном фильтре может наблюдаться
пять различных режимов течений. По порядку распространения на практике это
будут следующие режимы: линейный-линейный; линейный-переходный; переход-
ный-переходный; переходный-нелинейный; нелинейный-нелинейный. Наиболее
часто встречается первый режим (линейная фильтрация в ПЗС и линейная фильт-
рация в гравийном фильтре). Следующий линейный-переходный (линейный ре-
жим фильтрации в ПЗС и переходный от линейного у подошвы пласта к нелиней-
ному у кровли пласта) режим течения встречается реже для фильтрации нефти и
чаще для фильтрации воды. (Хотя, строго говоря, остальные четыре режима, полу-
чены из анализа линейного решения задачи, поэтому в отношении их вывод носит
лишь прогностический характер). Остальные режимы будут встречаться ещё более
редко.
4). Подчеркнем, что формулы (20), (22) и (24), полученные на основании (10) и
(12), больше носят качественный характер. Нужно помнить, что в предложенной
теории пренебрегли искривлением линий тока у ствола скважины. Поэтому значе-
ние выведенных формул (10) и (12) не столько в точных количественных оценках,
сколько в том, что с их помощью удается сравнительно просто выявить основные
фильтрационные эффекты, вызванные взаимодействием потока флюида в ПЗС с
течением в фильтре скважины.
4.4. Точное решение задачи фильтрации к скважине с гравийным фильтром
при линейном законе Дарси
4.4.1 Постановка задачи
В задачах подземной гидромеханики при расчетах дебитов скважин поверх-
ность их ствола принимается в качестве поверхности с постоянным значением
приведенного давления [41, 44, 108, 109 и др.]. Так как напор
g
P
H
ρ
=
и потенциал
