Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.

181
O11O
O
1
2
O
2
O1
2
O
O
O
2
O
2
O
O
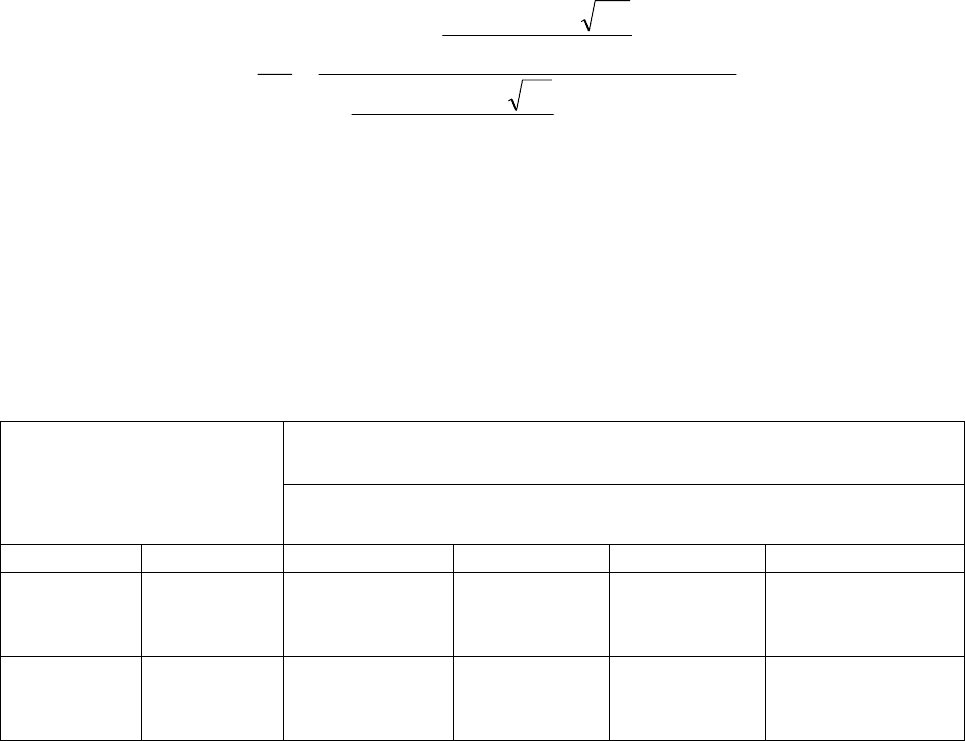
rln)1(
R2
DrR
ln
R2
D1R
ln
Q
Q
⋅−α+
+−+
+−+
=
l
l
(23)
где
()
2
O
2
O
2
2
O1
2
O
2
O1
R4rRD ll −−+= , а остальные обозначения те же, что и выше.
Влияние скачка проницаемости на дебит скважины, рассчитанное по формуле
(23 ), приводится в таблице 4.5.
Таблица 4.5.
Результаты расчётов отношений Q/Q0 по формуле (23).
Пример №2
l
0
= 0,5⋅R
0
R
0
r
10
k
1
/k
0
50 100 200 1000
5
0,5
2,0
20,0
0,69
1,29
1,73
0,73
1,23
1,55
0,76
1,19
1,44
0,80
1,14
1,30
10
0,5
2,0
20,0
0,61
1,48
2,56
0,65
1,37
2,03
0,69
1,30
1,78
0,74
1,21
1,49
Отметим, что расчёт
0
/ QQ , выполненный для примера №1 по формулам (10)
и (14) для исходных данных таблицы 4.4 привел с точностью до 0,01 к таким же
результатам, что и формула (22). Для примера № 2 расчет по формулам (10) и (16)
для данных таблицы 4.5 тоже с точностью до 0,01 приводит к результатам, совпа-
дающим с формулой (23). Всё это позволяет сделать вывод о практической равно-
ценности методов расчёта дебитов скважин с кусочно – однородной призабойной
зоной, предложенных в пунктах 4.9.3 и 4.9.4.
Результаты расчётов в таблицах 4.4 и 4.5 показывают, что увеличивая про-
ницаемость призабойной зоны скважины можно заметно увеличить её дебит.
Ухудшение проницаемости призабойной зоны по сравнению с проницаемостью
всего пласта приводит к резкому сокращению дебита скважины (см. строки для
5,0/
01
=kk
). Именно поэтому в эксплуатационной практике водо – и нефтедобы-
вающих скважин должны быть предусмотрены меры защиты призабойной зоны от
ухудшения со временем её фильтрационных свойств.

182
4.10. Математическое моделирование фильтрации к скважине с верти-
кальными трещинами гидроразрыва
Для повышения производительности работы нефтедобывающих скважин в их
призабойных зонах осуществляется специальная технологическая операция – гид-
роразрыв пласта. Эта операция может проводиться в двух режимах – вертикаль-
ный гидроразрыв пласта, когда создаются исходящие от ствола скважины трещи-
ны по всей толщине пласта, и горизонтальный гидроразрыв пласта, при котором
создаются трещины в виде круговых колец с центром на стволе скважины, распо-
ложенных горизонтально подошве и кровле пласта.
Для проектирования числа и размеров трещин, создаваемых с помощью гид-
роразрыва пласта, нужна соответствующая математическая модель.
Исследованию эффективности вертикального гидроразрыва пласта уделялось
внимание в работах многих авторов: Ентова В.М. и Мурзенко В.В. [54], Донцо-
ва К.М. с соавторами [53, 55], Кадета В.В. и Селякова В.И. [63], Каневской Р.Д. и
Кац Р.М. [64, 65] Зазовского А.Ф. и Тодуа Г.Т. [57], Доманского А.В. [52] и др. В
их работах при расчёте течений к вертикальным трещинам гидроразрыва учитыва-
ется конечная проницаемость, протяжённость и толщина (раскрытие) трещин.
Учёт всех перечисленных параметров достигается применением сложного матема-
тического аппарата. Для исследования течений к вертикальным трещинам гидро-
разрыва с учётом всех этих же параметров и, кроме того, при дополнительном учё-
те разных проницаемостей трещин и разных раскрытий, может быть применена
разработанная автором в 6-ой главе диссертации теория расчётов течений в много-
слойных средах. Для первоначальных прогностических расчётов, учитывающих
лишь количество трещин, проницаемость которых принимается бесконечно боль-
шой по сравнению с проницаемостью пласта, и их протяжённость, автор предло-
жил модифицированный вариант метода СВП.
Постановка задачи.
Продуктивный пласт считается однородным и изотроп-
ным и, поэтому, потенциал скорости фильтрации
ϕ
удовлетворяет уравнению Ла-
пласа. Основной фрагмент области фильтрации, для которого проводится расчёт,
представляет половину сектора между двумя соседними щелями (рис.52), где ϕ
щ
–
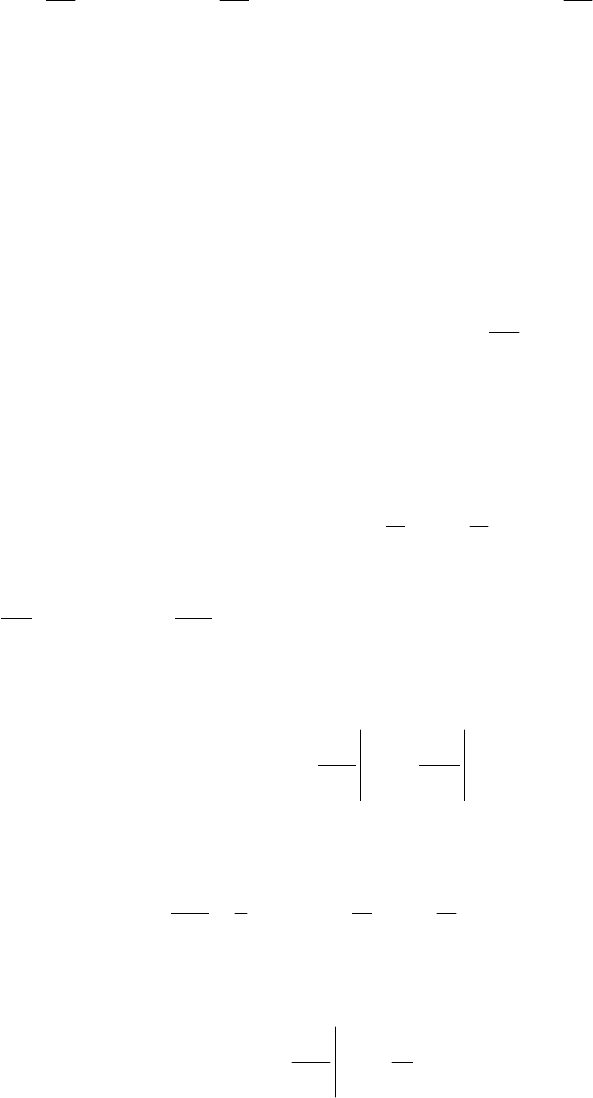
183
заданное значение потенциала на поверхности трещины, ϕ
П
– заданное значение
потенциала на контуре питания, К
щ
– количество трещин, R
П
– радиус контура пи-
тания, l- длина трещины, r
c
– радиус скважины, r, θ- полярные координаты. В соот-
ветствии с рис.52 и с учётом симметрии основного фрагмента DABC области
фильтрации, для уравнения Лапласа ∆ϕ = 0 запишем следующие граничные усло-
вия:
на
AB : 0
r
=
∂
ϕ∂
, на BC : 0=
θ∂
ϕ
∂
, на CD :
П
ϕ
=
ϕ
, на DE: 0=
θ∂
ϕ
∂
, на EA :
щ
ϕ
=
ϕ
, (1)
где (
AB - непроницаемый участок скважины, AE - трещина, CD - граница области
питания). Течение жидкости подчиняется закону Дарси.
Для решения задачи разделим область течения жидкости на две части. В об-
ласти 2 рассмотрим течение жидкости к фиктивной скважине радиуса
lrr
c
+
=
1
.
Решение задачи в этой области имеет вид:
⋅+=
п
п
R
r
Ar
ln),(
2
ϕθϕ
(2)
где
A - пока неизвестный параметр. В области 1 решение задачи находится мето-
дом Фурье и имеет вид:
∑
∞
=
λ
λ
θ⋅λ⋅
+
⋅+ϕ=θϕ
0n
n
c
c
nщ1
)sin(
r
r
r
r
C),r(
n
n
, (3)
где
()
щ
n
K
,1n2
2
π
=α+
α
π
=λ
. Так как радиальная составляющая скорости фильтра-
ции жидкости на границе
1
rr = неразрывна, то должно выполняться условие
11
rr
2
rr
1
rr
==
∂
ϕ∂
=
∂
ϕ∂
. (4)
Поскольку
)sin(
r
r
r
r
C
r
1
r
n
0n
c
c
nn
1
n
n
θ⋅λ
−
λ=
∂
ϕ∂
∑
∞
=
λ
λ
(5)
и
1
rr
2
r
A
r
1
=
∂
ϕ∂
=
, (6)
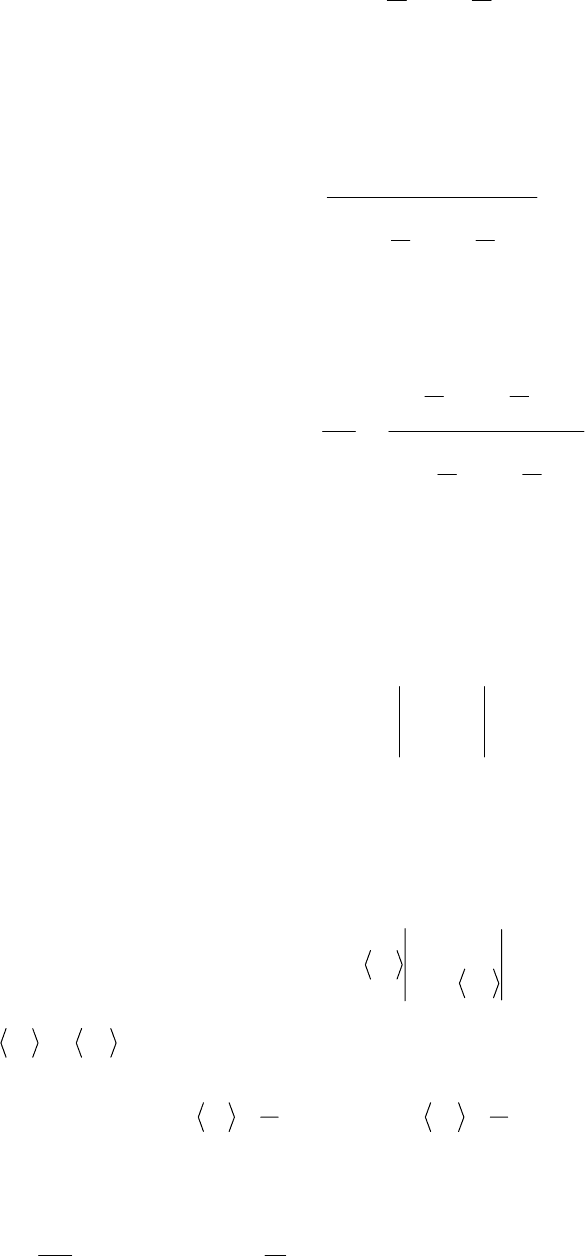
18
4
то из граничного условия (4) получим:
)sin(
r
r
r
r
CA
n
0n
1
c
c
1
nn
n
n
θλ
−
λ=
∑
∞
=
λ
λ
. (7)
Система функций
(){}
θλ
n
sin на отрезке
α
≤
θ
≤
0 ортогональна. Поэтому, умножая
обе части уравнения (7) на
(
)
θ
λ
n
sin и интегрируя по
θ
от 0 до
α
, получим:
−
αλ
=
λ
λ
n
n
1
c
c
1
n
n
r
r
r
r
A2
C
. (8)
После подстановки
n
C из (8) в (3) найдем, что:
)sin(
r
r
r
r
r
r
r
r
A2
),r(
n
0n
1
c
c
1
2
n
c
c
щ1
n
n
n
n
θλ
−
λ
+
α
+ϕ=θϕ
∑
∞
=
λ
λ
λ
λ
. (9)
В данной формуле осталась неизвестной константа A. Для её нахождения исполь-
зуем граничное условие неразрывности давления (а, значит, и функции ϕ) на дуге
окружности r = r
1
:
11
rr
2
rr
1
==
ϕ=ϕ . (10)
Точно в предлагаемом приближенном методе граничному условию (10) удовле-
творить не удается. Поэтому условие (10) выполним в осредненной форме, заме-
нив его на
2
1
rr
2rr
1
=
=
ϕ=
ϕ
, (11)
где
1
ϕ
и
2
ϕ
- средние арифметические значения:
∫∫
αα
θθϕ
α
=ϕθθϕ
α
=ϕ
0
122
0
111
d),r(
1
,d),r(
1
. (12)
Вычислив интегралы (12), из (11) для
A получим уравнение
+ϕ⋅α=⋅
α
+α⋅ϕ
R
r
lnAS
A2
1
пщ
, в котором через S обозначена сумма ряда

185
∑
∞
=
λ
λ
λ
λ
−
λ
+
=
0n
1
c
c
1
3
n
1
c
c
1
n
n
n
n
r
r
r
r
r
r
r
r
S
.
Из последнего уравнения для
A находим следующее значение:
(
)
S
2
r
R
ln
A
1
пщ
⋅
α
+
⋅α
ϕ
−
ϕ
⋅
α
−= . (13)
Теперь, когда константа
A найдена, можно вычислить дебит Q скважины, содер-
жащей
щ
K щелей. Этот дебит равен притоку к фиктивной скважине радиуса
1
r , т.е.
(
)
S
2
r
R
ln
2
A2Q
1
пщ
α
+
α
ϕ−ϕπα
=π=
. Для практического анализа полученной формулы удобнее
рассматривать отношение
0
Q
Q
, где
0
Q - дебит центральной круговой скважины ра-
диуса
0
r , работающей в таком же точно пласте и при тех же условиях и вычисляе-
мый по формуле Дюпюи. Для отношения
0
Q
Q
после элементарных преобразований
окончательно получаем следующий результат:
щ1
c
0
Kr
R
ln
r
R
ln
Q
Q
β
+
=
, где
∑
∞
=
λ
λ
λ
λ
−
+
+
π
=β
0n
1
c
c
1
3
1
c
c
1
2
n
n
n
n
r
r
r
r
)1n2(
r
r
r
r
16
. (14)
Для уверенного практического применения приближенной формулы (14) нужно
знать её точность. Для оценки этой точности проводились сопоставления расчетов
по формуле (14) для двух (
2
=
щ
K ) щелей с длиной
c
rl >> и по точной формуле
притока жидкости к прямолинейной центральной трещине длиной
l2 в круговом
пласте. Эта точная формула для частного случая
2
=
щ
K получается на основе пе-
рехода по методу ЭГДА от аналогичной формулы (4-40) в [62] для расчета элек-
трической емкости пластины в оболочке круглого сечения. Выполнив переход по

186
методу ЭГДА, для дебита скважины с 2
=
щ
K получим следующий точный резуль-
тат:
)k(K
)k(K
r
R
ln
Q
Q
0
0
щ2
π
′
=
, (15)
где
)(kK - полный эллиптический интеграл первого рода; );()( kKkK
′
=
′
2
1 kk −=
′
,
k - модуль эллиптического интеграла, вычисляемый по формуле
2
0
0
lrR
lrR
k
++
−−
=
.
Погрешность формулы (14) для
2
=
щ
K представлена на рис.53. Анализ показал,
что:
1. Формула (14) дает всегда заниженное по сравнению с точным значение де-
бита
Q ;
2. Для щелей с практически реальной длиной прострела
0
300rl ≤ относитель-
ная погрешность в среднем составляет 5% и не превосходит 8%. Такая точность
для практики приемлема.
Формула (14) была применена для анализа эффективности вертикального
гидравлического разрыва пласта в призабойной зоне скважины. В частности, ре-
зультаты расчетов
0
Q
Q
при 2500
0
=
r
R
приведены для различных
0
r
l
в таблице 4.6 и
представлены графически на рис.54.
Таблица 4.6
Дебит скважины с вертикальными трещинами при 2500
r
R
0
= .
Количество трещин
l / r
0
1 2 4 6 8 10 12 14 16 18 20
26,00 1,231 1,453 1,579 1,626 1,650 1,665 1,675 1,683 1,688 1,692 1,696
101,00 1,858 1,931 2,158 2,246 2,293 2,322 2,342 2,356 2,367 2,375 2,382
251,00 1,950 2,486 2,876 3,034 3,120 3,174 3,2111 3,238 3,258 3,275 3,288
301,00 2,043 2,638 3,080 3,263 3,363 3,425 3,469 3,500 3,524 3,543 3,558
401,00 2,210 2,919 3,471 3,705 3,834 3,916 3,972 4,014 4,045 4,070 4,090
По результатам расчетов можно сделать следующие выводы.

187
1. Дебит скважины с щелями существенно зависит от радиусов вертикальных
трещин. С ростом радиуса трещин дебит значительно растёт.
2. С ростом числа щелей дебит растёт, но быстро из-за интерференции щелей
достигает своего асимптотического значения. Оптимальное число трещин при
производстве гидроразрыва пласта от 2 до 4.
3. Выгоднее создавать небольшое количество (например, 2) крупных по раз-
мерам щелей, чем большое количество мелких трещин. Например, 20 щелей с
26
0
=
r
l
дают дебит 696,1
0
=
Q
Q
, в то же время 4 трещины с 301
0
=
r
l
дадут дебит поч-
ти в 2 раза больший
1,3
0
=
Q
Q
(см. рис.54).
Все выводы, к которому здесь привёл модифицированный метод СВП, согла-
суются с выводами других авторов [112] как по количеству, так и по и размерам
вертикальных трещин гидроразрыва. В контрольных расчётах вновь подтверди-
лось, что вычисленные методом СВП фильтрационные потоки имеют заниженное
на 5-8% значение. Это позволяет рекомендовать модифицированный метод СВП в
качестве простого оценочного метода в практических инженерных расчётах.
4.11. Математическое моделирование фильтрации к скважине с горизонталь-
ными трещинами гидроразрыва
Операция горизонтального гидроразрыва пласта (ГГРП), осуществляемая с
целью повышения производительности нефтедобывающих скважин, описана в
[112]. Здесь же приведена формула (Х.46) С.А. Христиановича и Ю.П. Желтова,
полученная по данным электролитического моделирования, с помощью которой
оценивается эффективность ГГРП для некоторых параметров
b , l,
0
r ,
1
r и
R
. Через
R
обозначен радиус кругового контура питания с центром, совпадающим с цен-
тром скважины, а остальные обозначения соответствуют принятым в [112] и при-
ведены на рис.55. Недостатком формулы (Х.46) является ограниченная область её
применения (которая в [112] не указана), низкая точность и пригодность к случаю
только одной трещины, расположенной строго в середине пласта.

188
Приближённое аналитическое решение о притоке к скважине с одной сере-
динной горизонтальной трещиной на основе метода ЭГДА получено Василье-
вым Ю.Н. и Башкировым А.И. в [27].
В данной работе автором представлена на основе модифицированного метода
СВП математическую модель фильтрации нефти как к одиночной горизонтальной
трещине (ГТ), так и к нескольким параллельным и одинаковым по размерам ГТ,
расположенным в виде гирлянды вдоль ствола скважины. Ствол скважины счита-
ется непроницаемым, а добыча нефти осуществляется только через одну или не-
сколько ГТ.
Осесимметричное фильтрационное течение к ГТ на рис.55 будем порознь рас-
сматривать в каждом из фрагментов, отделённых друг от друга плоскостью
l−= bz . В первом приближении эту плоскость можно принять за поверхность то-
ка, что точно выполняется при серединном расположении трещины и приближён-
но – для остальных положений.
В свою очередь, каждый из фрагментов разобьем на подфрагменты: соответ-
ственно на 1-ю и 2-ю зоны и примыкающие к ним внешние области, ограниченные
цилиндрической поверхностью
R
r
=
. Второе допущение, которое примем для
приближённого расчёта исследуемого осесимметричного течения, заключается в
том, что скорость фильтрации на границах
10
rrr
+
=
первой и второй зон в соответ-
ствии с методом СВП будем считать постоянными величинами v
1
и v
2
, подлежа-
щими определению из граничных условий задачи.
Третье допущение, принятое в рассматриваемой задаче – допущение о том,
что гидростатическая составляющая
gz
ρ
в приведённом давлении gzpp
ρ
+=
*
ма-
ло изменяется по толщине пласта по сравнению с действующими значениями гид-
родинамического давления
p
. В связи со сказанным будем считать, что в законе
Дарси
;gradv
ϕ
=
r
;
kp
*
µ
−=ϕ
p
*
= p + ρgz (1)

189
2
b
constz
== . Рассмотрим теперь при сделанных допущениях решение задачи ли-
нейной напорной фильтрации в однородном изотропном пласте в 1 – ой зоне.
Для
линейного закона Дарси потенциал φ скорости фильтрации должен удовлетворять
уравнению Лапласа
∆ϕ =
0
rr
r
rr
1
2
2
=
∂
ϕ∂
+
∂
ϕ∂
∂
∂
⋅ (2)
и граничным условиям
;0
r
0
rr
=
∂
ϕ∂
=
1
rrr
v
r
10
=
∂
ϕ∂
+=
, ;0
z
0z
=
∂
ϕ∂
=
Щ
Lbz
ϕ=ϕ
−=
. (3)
Решение краевой задачи (2), (3) ищем в виде суммы φ = φ
Щ
+ U(r, z). Поскольку
φ
Щ
= const, то функция U(r, z) тоже должна будет удовлетворять уравнению (2).
Граничные же условия для U(r, z) совпадут с граничными условиями (3), за исклю-
чением последнего, которое следует заменить на
0U
bz
=
−= l
. (4)
Решение граничной задачи для U(r, z) находится методом Фурье, после чего для
потенциала φ
1
(r, z) в 1 – ой зоне получаем выражение:
()
(
)
(
)
()
()
∑
∞
=
λ⋅
+⋅λ
⋅−
⋅
−
+ϕ=ϕ
0n
n
10n
2
n
n
n
1
Щ1
zcos
rrw
rW1
b
v2
z,r
l
(5)
где
()
()
l−
+π
=λ
b2
1n2
n
, а W
n
(r) и w
n
(r) находятся по формулам
()
()
(
)
() ()
;
rKrI
rKrI
rW
0n10n1
n0n0
n
λλ
λ−λ
=
() ()
() ()
() ()
0n10n1
n1n1
n
n
n
rKrI
rKrI
rW
1
rw
λλ
λλ
=
′
⋅
λ
=
. (6)
Здесь через I
0
(x), I
1
(x) обозначены модифицированные функции Бесселя, а через
K
0
(x) и K
1
(x) – цилиндрические функции Макдональда 0-го и 1-го порядков [131].
Из полученного решения (5) можно вычислить среднее значение <φ
1
> на гранич-
ной цилиндрической поверхности r = r
0
+ r
1
первой зоны:
()
∫
−
⋅+ϕ⋅
−
=ϕ
l
l
b
0
1011
dzz,rr
b
1
. (7)
После вычисления интеграла (7) и алгебраических преобразований придём к сле-
дующему значению для среднего:
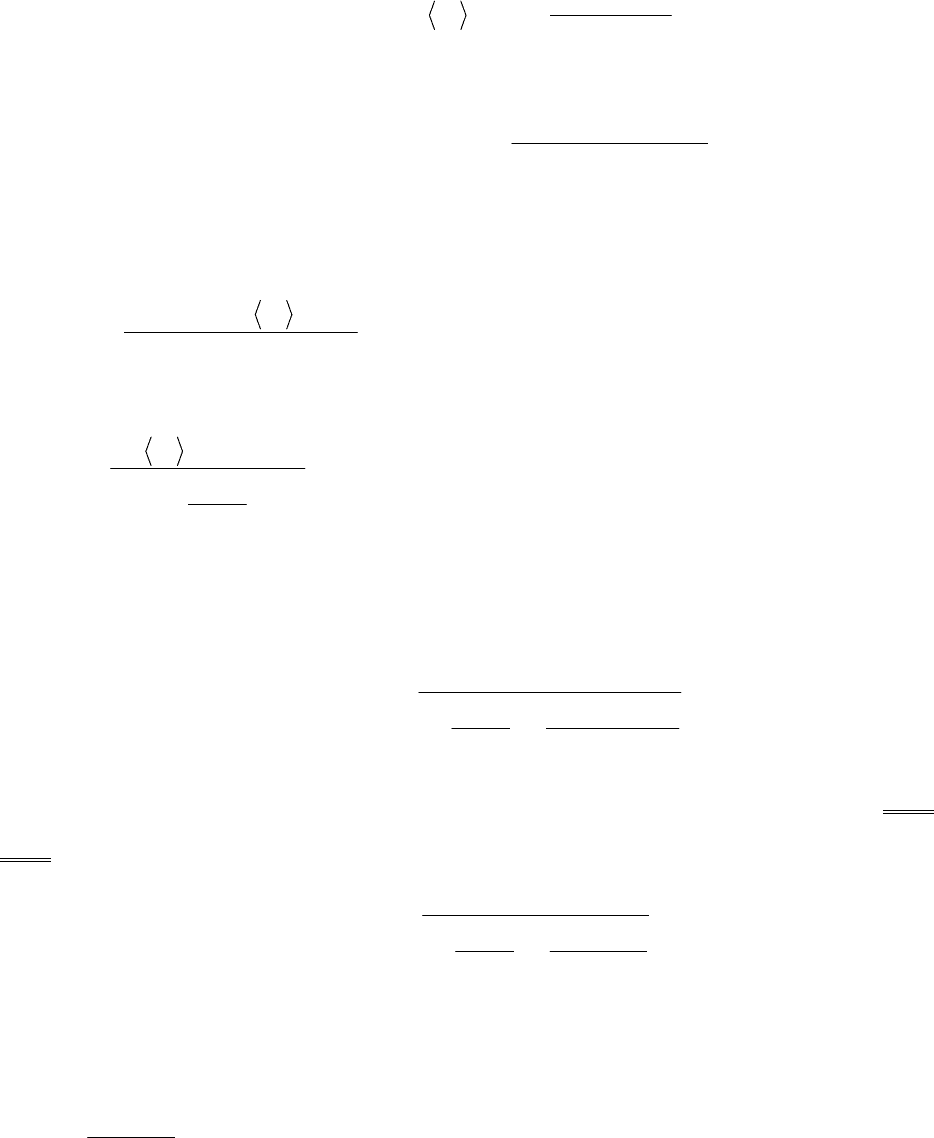
190
(
)
1
3
1
Щ1
S
vb16
⋅
π
⋅
−
+ϕ=ϕ
l
, (8)
где S
1
– сумма числового ряда
(
)
()()
∑
∞
=
+⋅+
+
=
0n
10n
3
10n
1
rrw1n2
rrW
S
. (9)
Формула (8) совместно с выражением для v
1
на рис.55 позволяет выразить приток
Q
1
флюида к ГТ в 1-ой зоне через заданное значение потенциала φ
Щ
и среднее
<φ
1
>:
()
()
1
Щ110
4
1
S8
rr
Q
⋅
ϕ−ϕ⋅+⋅π
=
. C другой стороны, для притока Q
1
в области,
примыкающей в первом фрагменте к 1– ой зоне, по формуле Дюпюи имеем значе-
ние:
(
)
()
+
−ϕ−ϕπ
=
10
П1
1
rr
R
ln
b2
Q
l
, где ϕ
П
– заданное значение потенциала на контуре пи-
тания r = R. Исключая из двух последних равенств общее неизвестное значение
<φ
1
>, окончательно для Q
1
получим выражение
(
)
(
)
()
()
10
3
1
10
ПЩ
1
rr
bS16
rr
R
ln
b2
Q
+π
−⋅⋅
+
+
−ϕ−ϕπ
=
l
l
(10)
Выполняя совершенно аналогичные расчёты для исследования течения во 2-ой
зоне, для притока Q
2
к ГТ из второго фрагмента получим значение
(
)
()
10
3
2
10
ПЩ
2
rr
S16
rr
R
ln
2
Q
+π
⋅⋅
+
+
⋅ϕ−ϕπ
=
l
l
(11)
где S
2
– сумма числового ряда, определяемого как и выше по формуле (9), с той
лишь разницей, что собственные значения λ
n
теперь будут вычисляться по форму-
ле
()
l⋅
+π
=λ
2
1n2
n
. Складывая Q
1
и Q
2
мы и получим полный приток Q к одиночной
ГТ, изображённой на рис55. Формулу для суммы Q = Q
1
+ Q
2
приведём в виде,
удобном для вычислений на ЭВМ.
