Тиманюк В.А., Животова Е.Н. Биофизика

Подождите немного. Документ загружается.

Êèíåòè÷åñêàÿ ýíåðãèÿ òåë, ñîâåðøàþùèõ îäíîâðåìåííî ïî-

ñòóïàòåëüíîå è âðàùàòåëüíîå äâèæåíèÿ, ðàâíà àðèôìåòè÷åñêîé

ñóììå ýíåðãèé îáîèõ òèïîâ äâèæåíèé:

кин

mv I

. (2.2.47)

Õàðàêòåðèñòèêè è óðàâíåíèÿ äèíàìèêè ïîñòóïàòåëüíîãî è âðà-

ùàòåëüíîãî äâèæåíèé ñîïîñòàâëåíû â òàáë. 2.2.1.

Ò à á ë è ö à 2.2.1

Õàðàêòåðèñòèêè è óðàâíåíèÿ äèíàìèêè ïîñòóïàòåëüíîãî

è âðàùàòåëüíîãî äâèæåíèé

Ïîñòóïàòåëüíîå äâèæåíèå Âðàùàòåëüíîå äâèæåíèå

Ìàññà m Ìîìåíò èíåðöèè I

Ñèëà

Ìîìåíò ñèëû

Èìïóëüñ P

Ìîìåíò èìïóëüñà L

Ïåðâûé çàêîí Íüþòîíà

constv =

èëè

0v =

ïðè =

∑

F constω=

èëè 0ω=

ïðè =

∑

Âòîðîé çàêîí Íüþòîíà

∑

Fma =ε

∑

Òðåòèé çàêîí Íüþòîíà

=−

12 21

FF =−

12 21

Çàêîí ñîõðàíåíèÿ èìïóëüñà

Çàêîí ñîõðàíåíèÿ ìîìåíòà

èìïóëüñà

constP

constL

Ðàáîòà

AFr=∆

AM=∆ϕ

Êèíåòè÷åñêàÿ ýíåðãèÿ

кин

E =

кин

Çàêîí ñîõðàíåíèÿ ýíåðãèè

пот

const

E+=

пот

const

Ìîùíîñòü

NFv

==ω

§ 2.2. Äèíàìèêà

§ 2.3. ÌÅÕÀÍÈ×ÅÑÊÈÅ ÊÎËÅÁÀÍÈß

Ìåõàíè÷åñêèìè êîëåáàíèÿìè, èëè êîëåáàòåëüíûì äâèæåíèåì,

íàçûâàþòñÿ äâèæåíèÿ òåë, õàðàêòåðèçóþùèåñÿ òîé èëè èíîé ñòå-

ïåíüþ ïîâòîðÿåìîñòè ÷åðåç îïðåäåëåííûå ïðîìåæóòêè âðåìåíè.

Äëÿ õàðàêòåðèñòèêè êîëåáàíèé ââîäÿòñÿ ñëåäóþùèå âåëè÷èíû:

1) îòêëîíåíèå, èëè ñìåùåíèå x, îò ïîëîæåíèÿ ðàâíîâåñèÿ:

==+

(), ( ),xftxftT

(2.3.1)

ãäå ()ft — ïåðèîäè÷åñêàÿ ôóíêöèÿ âðåìåíè;

2) àìïëèòóäà À êîëåáàíèÿ — ìàêñèìàëüíîå îòêëîíåíèå îò ïî-

ëîæåíèÿ ðàâíîâåñèÿ;

3) ïåðèîä Ò — äëèòåëüíîñòü îäíîãî ïîëíîãî êîëåáàíèÿ;

4) ÷àñòîòà ν — ÷èñëî êîëåáàíèé â åäèíèöó âðåìåíè,

ν=

;

(2.3.2)

5) êðóãîâàÿ, èëè öèêëè÷åñêàÿ, ÷àñòîòà:

ω= πν=

; (2.3.3)

5) ôàçà êîëåáàíèÿ:

=ω +

t . (2.3.4)

ãäå

— íà÷àëüíàÿ ôàçà ïðè

Ôàçà îïðåäåëÿåòñÿ ñ òî÷íîñòüþ äî ïðîèçâîëüíîãî ñëàãàåìîãî,

êðàòíîãî 2π. Ïîýòîìó îáû÷íî ðàññìàòðèâàþòñÿ çíà÷åíèÿ ϕ

, ëåæà-

ùèå â ïðåäåëàõ îò –π äî +π.

Åäèíèöû èçìåðåíèÿ ýòèõ âåëè÷èí: ÷àñòîòà

ν[]

= Ãö = ñ

—1

; ïå-

ðèîä

[]T

= ñ; öèêëè÷åñêàÿ ÷àñòîòà

ω[]

= ðàä/ñ; àìïëèòóäà è ñìå-

ùåíèå

=[] []Ax

= ì.

Íèæå áóäóò ðàññìîòðåíû òàê íàçûâàåìûå ãàðìîíè÷åñêèå êîëå-

áàíèÿ, òî åñòü êîëåáàíèÿ, ïðè êîòîðûõ êîëåáëþùàÿñÿ âåëè÷èíà

èçìåíÿåòñÿ ïî çàêîíó ñèíóñà èëè êîñèíóñà.

Íåçàòóõàþùèå ãàðìîíè÷åñêèå êîëåáàíèÿ. Ãàðìîíè÷åñêèå êîëå-

áàíèÿ ñîâåðøàþòñÿ ïîä äåéñòâèåì óïðóãèõ èëè êâàçèóïðóãèõ

ñèë,

îïèñûâàåìûõ çàêîíîì Ãóêà:

=−

Fkx

, (2.3.5)

Êâàçèóïðóãèìè íàçûâàþòñÿ ñèëû, íåóïðóãèå ïî ïðèðîäå, íî àíàëîãè÷íûå ïî

ñâîéñòâàì óïðóãèì, âîçíèêàþùèå ïðè ìàëûõ äåôîðìàöèÿõ óïðóãèõ òåë. Â êà÷å-

ñòâå ïðèìåðà êâàçèóïðóãèõ ñèë ìîæíî ïðèâåñòè ñèëû, ïîä äåéñòâèåì êîòîðûõ

êîëåáëåòñÿ ìàòåìàòè÷åñêèé ìàÿòíèê.

Ãëàâà 2. Ìåõàíèêà

ãäå F — âîçâðàùàþùàÿ ñèëà; x — ñìåùåíèå îò ïîëîæåíèÿ ðàâ-

íîâåñèÿ (ãäå

); k — êîýôôèöèåíò êâàçèóïðóãîé ñèëû, èëè

æåñòêîñòü. Çíàê «—» óêàçûâàåò íà òî, ÷òî âîçâðàùàþùàÿ ñèëà ñòðå-

ìèòñÿ âåðíóòü òåëî â èñõîäíîå ïîëîæåíèå, òî åñòü íàïðàâëåíà ïðî-

òèâ ñìåùåíèÿ.

Ñîãëàñíî âòîðîìó çàêîíó Íüþòîíà, óðàâíåíèå (2.3.5) ìîæåò

áûòü ïðîáðàçîâàíî ó âèäó

=−

ma kx

, (2.3.6)

ãäå ò — ìàññà êîëåáëþùåãîñÿ òåëà.

Ó÷èòûâàÿ, ÷òî

, è ââåäÿ îáîçíà÷åíèå

ω=

ïîëó÷àåì

+ω =

. (2.3.7)

Óðàâíåíèå (2.3.7) ÿâëÿåòñÿ äèôôåðåíöèàëüíûì óðàâíåíèåì

íåçàòóõàþùèõ ãàðìîíè÷åñêèõ êîëåáàíèé. Åãî ðåøåíèå èìååò âèä

() ( )

cosxt A t=ω+ϕ

, (2.3.8)

èëè

() ( )

sinxt A t=ω+ϕ

Äëÿ ëþáûõ íåçàòóõàþùèõ ãàðìîíè÷åñêèõ êîëåáàíèé ñïðàâåä-

ëèâû ôîðìóëû:

ω=

;

ν=

;

=π

. (2.3.9)

Ïåðèîäû êîëåáàíèé äëÿ ïðîñòåéøèõ êîëåáàòåëüíûõ ñèñòåì:

ìàòåìàòè÷åñêîãî ìàÿòíèêà — ìàòåðèàëüíîé òî÷êè, ïîäâåøåí-

íîé íà íèòè,

==π

, (2.3.10)

ãäå l — äëèíà ìàÿòíèêà; g — óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ;

ïðóæèííîãî ìàÿòíèêà — ìàòåðèàëüíîé òî÷êè, ïîäâåøåííîé íà ïðó-

æèíå,

=π

, (2.3.11)

ãäå k — æåñòêîñòü ïðóæèíû;

§ 2.3. Ìåõàíè÷åñêèå êîëåáàíèÿ

ôèçè÷åñêîãî ìàÿòíèêà — òâåðäîãî òåëà, ñîâåðøàþùåãî ïîä äåé-

ñòâèåì ñèëû òÿæåñòè êîëåáàíèÿ âîêðóã ãîðèçîíòàëüíîé îñè ïîä-

âåñà,

=π2

mgl

ãäå I — ìîìåíò èíåðöèè ôèçè÷åñêîãî ìàÿòíèêà îòíîñèòåëüíî îñè,

ïðîõîäÿùåé ÷åðåç òî÷êó ïîäâåñà; l — ðàññòîÿíèå ìåæäó òî÷êîé

ïîäâåñà è öåíòðîì òÿæåñòè ìàÿòíèêà.

Ñêîðîñòü è óñêîðåíèå ìàòåðèàëüíîé òî÷êè ïðè ãàðìîíè÷å-

ñêîì êîëåáàíèè ðàâíû ñîîòâåòñòâåííî:

() ()

==−ωω+ϕ=

sin

vt A t

ππ



=ω ω+ϕ+ = ω+ϕ+





0max 0

cos cos

At v t ; (2.3.12)

() ()

===−ω ω+ϕ=

cos

at A t

()()

= ω ω+ϕ+π= ω+ϕ+π

0max 0

cos cosAt a t , (2.3.13)

ãäå

=ω

max

vA — ìàêñèìàëüíàÿ ñêîðîñòü (àìïëèòóäà ñêîðîñòè);

=ω

max

aA — ìàêñèìàëüíîå óñêîðåíèå (àìïëèòóäà óñêîðåíèÿ).

Òàêèì îáðàçîì, ñêîðîñòü è óñêîðåíèå, òàê æå êàê è ñìåùåíèå,

èçìåíÿþòñÿ ïî ãàðìîíè÷åñêîìó çàêîíó. Ñðàâíèâ âûðàæåíèÿ (2.3.8),

(2.3.12) è (2.3.13) çàìå÷àåì, ÷òî ñêîðîñòü îïåðåæàåò ñìåùåíèå ïî

ôàçå íà

, à óñêîðåíèå — íà π, òî åñòü ñìåùåíèå è óñêîðåíèå

íàõîäÿòñÿ â ïðîòèâîôàçå (ðèñ. 2.3.1).

Ðèñ. 2.3.1. Ãðàôè÷åñêèå çàâèñèìîñòè ñìåùåíèÿ x, ñêîðîñòè v è óñêîðåíèÿ a

Ãëàâà 2. Ìåõàíèêà

Êèíåòè÷åñêàÿ è ïîòåíöèàëüíàÿ ýíåðãèè ãàðìîíè÷åñêèõ êîëå-

áàíèé ðàâíû:

()

2222

кин 0

sin

EmvmA t

==ωω+

, (2.3.14)

()

222

пот 0

cos

EkxkA t

== ω+

. (2.3.15)

Ó÷èòûâàÿ, ÷òî

ω=

, ïîëíàÿ ýíåðãèÿ ãàðìîíè÷åñêèõ êîëåáà-

íèé ðàâíà:

22 22 2

111 1

222 2

Emv kx mA kA

=+=ω=

. (2.3.16)

Òàêèì îáðàçîì, ïîëíàÿ ýíåðãèÿ ãàðìîíè÷åñêèõ êîëåáàíèé

ñîõðàíÿåòñÿ:

кин пот

cons

EE E

=+=

, â òî âðåìÿ êàê êèíåòè÷åñêàÿ

è ïîòåíöèàëüíàÿ èçìåíÿþò-

ñÿ ïî ãàðìîíè÷åñêîìó çàêî-

íó, âçàèìíî ïðåâðàùàÿñü

äðóã â äðóãà (ðèñ. 2.3.2).

Çàòóõàþùèå êîëåáàíèÿ.

Â ðåàëüíûõ ôèçè÷åñêèõ ñèñ-

òåìàõ, ó÷àñòâóþùèõ â êîëå-

áàòåëüíîì äâèæåíèè, âñåãäà

ïðèñóòñòâóþò ñèëû ñîïðî-

òèâëåíèÿ, äåéñòâèå êîòîðûõ

óìåíüøàåò ýíåðãèþ ñèñòåìû.

Óìåíüøåíèå ýíåðãèè ïðîÿâëÿåòñÿ â çàòóõàíèè êîëåáàíèé.

Ïðè íå î÷åíü áîëüøèõ ñêîðîñòÿõ è àìïëèòóäàõ êîëåáàíèé ñèëà

ñîïðîòèâëåíèÿ ïðîïîðöèîíàëüíà ñêîðîñòè äâèæåíèÿ òåëà:

=− =−

Fr rv

, (2.3.17)

ãäå r — êîýôôèöèåíò ñîïðîòèâëåíèÿ èëè âÿçêîãî òðåíèÿ. Òàê êàê

âîçâðàùàþùàÿ ñèëà ïðîïîðöèîíàëüíà ñìåùåíèþ, òî èç âòîðîãî

çàêîíà Íüþòîíà

=− −

mkxr

(2.3.18)

ñëåäóåò äèôôåðåíöèàëüíîå óðàâíåíèå çàòóõàþùèõ êîëåáàíèé:

+β +ω =

, (2.3.19)

Ðèñ. 2.3.2. Çàâèñèìîñòè êèíåòè÷åñêîé Å

êèí

ïîòåíöèàëüíîé Å

ïîò

è ïîëíîé ýíåðãèè Å ñèñ-

òåìû îò âðåìåíè t

ïîò

êèí

§ 2.3. Ìåõàíè÷åñêèå êîëåáàíèÿ

ãäå β=

— êîýôôèöèåíò çàòóõàíèÿ, õàðàêòåðèçóþùèé ñòåïåíü

çàòóõàíèÿ êîëåáàíèé;

ω=

— ñîáñòâåííàÿ êðóãîâàÿ ÷àñòîòà

êîëåáàòåëüíîé ñèñòåìû, òî åñòü ÷àñòîòà, ñ êîòîðîé ñîâåðøàëèñü áû

ñâîáîäíûå êîëåáàíèÿ ñèñòåìû â îòñóòñòâèå ñîïðîòèâëåíèÿ ñðåäû

(ïðè

Ðåøåíèå ýòîãî óðàâíåíèÿ ïðè ñëàáîì çàòóõàíèè β < ω

ñëåäóþ-

ùåå:

()

ecos

xA t

−β

=ω+

, (2.3.20)

ãäå A

— àìïëèòóäà êîëåáà-

íèé â íà÷àëüíûé ìîìåíò âðå-

ìåíè (t =0); ω= ω −β

—

êðóãîâàÿ ÷àñòîòà çàòóõàþùèõ

êîëåáàíèé. Ãðàôèê ôóíê-

öèè (2.3.20) ïðèâåäåí íà

ðèñ. 2.3.3.

Äâèæåíèå ñèñòåìû ìîæ-

íî ðàññìàòðèâàòü êàê ãàðìî-

íè÷åñêîå êîëåáàíèå ñ ÷àñòî-

òîé ω è àìïëèòóäîé À,

èçìåíÿþùåéñÿ âî âðåìåíè

ïî çàêîíó:

()

AAt A

−β

== . (2.3.21)

Ïåðèîä çàòóõàþùåãî êîëåáàíèÿ

ω−β

. (2.3.22)

Çàòóõàþùèå êîëåáàíèÿ ïðèíÿòî õàðàêòåðèçîâàòü äåêðåìåíòîì

çàòóõàíèÿ

()

At T

(2.3.23)

èëè ëîãàðèôìè÷åñêèì äåêðåìåíòîì çàòóõàíèÿ

()

λ= =β

At T

. (2.3.24)

Ðèñ. 2.3.3. Çàòóõàþùèå êîëåáàíèÿ (

<ω

)

Ãëàâà 2. Ìåõàíèêà

Ëîãàðèôìè÷åñêèé äåêðåìåíò çàòóõàíèÿ λ òàê æå êàê è êîýô-

ôèöèåíò çàòóõàíèÿ β, õàðàêòåðèçóåò ñêîðîñòü óáûâàíèÿ àìïëèòó-

äû êîëåáàíèé.

Åñëè çàòóõàíèå â ñèñòåìå çíà÷èòåëüíî

>ω

(), òî â ýòîì ñëó-

÷àå äâèæåíèå ÿâëÿåòñÿ íåïåðèîäè÷åñêèì (àïåðèîäè÷åñêèì). Ñèñ-

òåìà âîçâðàùàåòñÿ â ïîëîæåíèå ðàâíîâåñèÿ, íå ñîâåðøàÿ êîëåáà-

íèé. Âîçìîæíû äâà âàðèàíòà òàêîãî âîçâðàùåíèÿ. Åñëè âûâåäåííîé

èç ïîëîæåíèÿ ðàâíîâåñèÿ ñèñòåìå ñîîáùàþò äîñòàòî÷íî ñèëüíûé

òîë÷îê (â ñòîðîíó ðàâíîâåñèÿ) òàê, ÷òî âîçâðàùåíèå ê èñõîäíîìó

ñîñòîÿíèþ ïðîèñõîäèò ñ íà÷àëüíîé ñêîðîñòüþ, îïðåäåëÿåìîé óñ-

ëîâèåì

()

>β+β−ω

00 0

xv , (2.3.25)

ãäå

x — ñìåùåíèå îò ïîëîæåíèÿ ðàâíîâåñèÿ, òî ïðîöåññ îïè-

ñûâàåòñÿ êðèâîé 1 (ðèñ. 2.3.4). Åñëè æå âîçâðàùåíèå ê ïîëîæå-

íèþ ðàâíîâåñèÿ ïðîèñõîäèò ñà-

ìîïðîèçâîëüíî — áåç òîë÷êà

èëè ñîïðîâîæäàåòñÿ òîë÷êîì

íåäîñòàòî÷íîé ñèëû äëÿ âûïîë-

íåíèÿ óñëîâèÿ (2.3.25),— òî

äâèæåíèå îïèñûâàåòñÿ êðèâîé

2 (ðèñ. 2.3.4).

Âûíóæäåííûå êîëåáàíèÿ. Äëÿ

ïîëó÷åíèÿ íåçàòóõàþùèõ êîëåáà-

íèé íåîáõîäèìî âîçäåéñòâèå

âíåøíåé ñèëû, ðàáîòà êîòîðîé

âîñïîëíÿëà áû âûçâàííîå ñèëà-

ìè ñîïðîòèâëåíèÿ óìåíüøåíèå

ýíåðãèè êîëåáëþùåéñÿ ñèñòåìû.

Òàêèå êîëåáàíèÿ íàçûâàþòñÿ âû-

íóæäåííûìè.

Åñëè êîëåáàòåëüíàÿ ñèñòåìà

ïîäâåðãàåòñÿ äåéñòâèþ âíåøíåé

ñèëû ñ àìïëèòóäîé

F , èçìåíÿ-

þùåéñÿ ïî ãàðìîíè÷åñêîìó çà-

êîíó c ÷àñòîòîé ω,

=ω

cosFF t

, (2.3.26)

òî èç âòîðîãî çàêîíà Íüþòîíà

=+ +

mFFF

(2.3.27)

Ðèñ. 2.3.4. Äâà âîçìîæíûõ ñïîñîáà âîç-

âðàùåíèÿ ñèñòåìû ê ïîëîæåíèþ ðàâ-

íîâåñèÿ ïðè àïåðèîäè÷åñêîì äâèæåíèè

(

β>ω

)

§ 2.3. Ìåõàíè÷åñêèå êîëåáàíèÿ

ñëåäóåò äèôôåðåíöèàëüíîå óðàâíåíèå âûíóæäåííûõ êîëåáàíèé :

+β +ω = ω

2cos

xf t

, (2.3.28)

ãäå β=

; ω=

; =

Ðåøåíèå óðàâíåíèÿ

(2.3.28) ñîñòîèò èç äâóõ

ñëàãàåìûõ. Îäíî èç íèõ

ñîîòâåòñòâóåò ïðîöåññó

óñòàíîâëåíèÿ êîëåáàíèé

(ðèñ. 2.3.5), ñî âðåìåíåì

èì ìîæíî ïðåíåáðå÷ü;

âòîðîå — óñòàíîâèâøèì-

ñÿ êîëåáàíèÿì.

Ðåøåíèå óðàâíåíèÿ

(2.3.28), îòâå÷àþùåå óñ-

òàíîâèâøèìñÿ êîëåáàíè-

ÿì, èìååò âèä:

()

=ω−αcosxA t , (2.3.29)

ãäå

()

ω−ω +βω

22 22

; (2.3.30)

ωβ

α=

ω−ω

arctg

. (2.3.31)

×àñòîòà âûíóæäåííûõ êîëåáàíèé ðàâíà ÷àñòîòå ω âûíóæäàþ-

ùåé ñèëû F

. Âûíóæäåííûå êîëåáàíèÿ ñäâèíóòû ïî ôàçå îòíîñè-

òåëüíî âûíóæäàþùåé ñèëû.

Èç ôîðìóëû (2.3.30) âèäíî, ÷òî àìïëèòóäà âûíóæäåííûõ êîëå-

áàíèé ïðÿìî ïðîïîðöèîíàëüíà àìïëèòóäå âûíóæäàþùåé ñèëû







è ñëîæíûì îáðàçîì çàâèñèò îò êîýôôèöèåíòà çàòóõàíèÿ

β, ñîáñòâåííîé êðóãîâîé ÷àñòîòû ω

è âíåøíåé ω. Ïðè íåêîòîðîì

çíà÷åíèè ω àìïëèòóäà äîñòèãíåò ñâîåãî ìàêñèìàëüíîãî çíà÷åíèÿ.

ßâëåíèå äîñòèæåíèÿ ìàêñèìàëüíîé àìïëèòóäû íàçûâàåòñÿ ðåçî-

íàíñîì, à ñîîòâåòñòâóþùàÿ ÷àñòîòà ω

ðåç

— ðåçîíàíñíîé.

Ðèñ. 2.3.5. Âûíóæäåííûå êîëåáàíèÿ

Ãëàâà 2. Ìåõàíèêà

Àìïëèòóäà äîñòèãàåò ìàêñèìàëüíîãî çíà÷åíèÿ, êîãäà çíàìåíà-

òåëü âûðàæåíèÿ (2.3.30) äîñòèãàåò ìèíèìàëüíîãî. Ïðîäèôôåðåí-

öèðîâàâ åãî ïî ω, ïðèðàâíÿâ íóëþ è ðåøèâ ïîëó÷åííîå óðàâíåíèå

îòíîñèòåëüíî ω, ïîëó÷àåì çíà÷åíèå ðåçîíàíñíîé ÷àñòîòû:

рез

ω=ω−β

2 . (2.3.32)

Ïîäñòàâèâ (2.3.32) â (2.3.30), ïîëó÷àåì çíà÷åíèå àìïëèòóäû ïðè

ðåçîíàíñå:

рез

βω−β

. (2.3.33)

Èç ôîðìóëû (2.3.32) âèäíî, ÷òî ÷åì ìåíüøå êîýôôèöèåíò çà-

òóõàíèÿ β, òåì áëèæå ðåçîíàíñíàÿ ÷àñòîòà ω

ðåç

ê ñîáñòâåííîé ω

Â ïðåäåëå ïðè

→

рез

ω→ω

рез

→∞A

. Ïðè î÷åíü áîëüøîì

çàòóõàíèè ( β>ω

2 ) âûðàæåíèå (2.3.32) ñòàíîâèòñÿ ìíèìûì è ðå-

çîíàíñ íå íàáëþäàåòñÿ. Ïðè

ýòîì ñ óâåëè÷åíèåì âíåøíåé

÷àñòîòû àìïëèòóäà âûíóæ-

äåííûõ êîëåáàíèé ìîíîòîí-

íî óìåíüøàåòñÿ (ñì. íèæ-

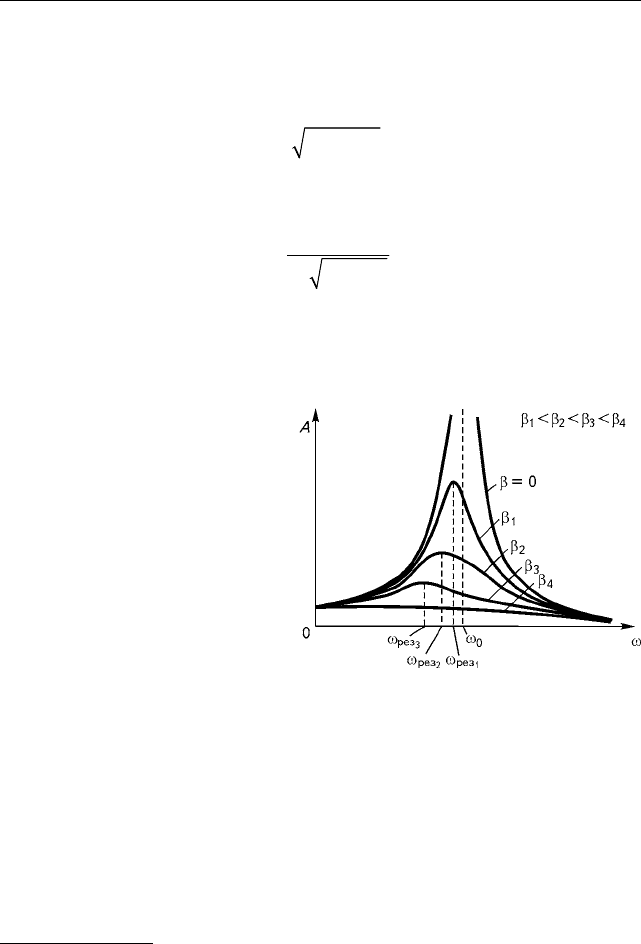
íþþ êðèâóþ íà ðèñ. 2.3.6).

Ãðàôè÷åñêèå çàâèñèìîñòè

àìïëèòóäû âûíóæäåííûõ

êîëåáàíèé

A îò âíåøíåé

÷àñòîòû ω, ñîîòâåòñòâóþùèå

ðàçëè÷íûì çíà÷åíèÿì êîýô-

ôèöèåíòà çàòóõàíèÿ β, ïðè-

âåäåíû íà ðèñ. 2.3.6. Òàêèå

êðèâûå íàçûâàþòñÿ ð å ç î-

íàíñíûìè.

Â æèâûõ îðãàíèçìàõ íàáëþäàåòñÿ ìíîæåñòâî êîëåáàòåëüíûõ

ïðîöåññîâ (áèåíèå ñåðäöà, ïóëüñàöèÿ êðîâåíîñíûõ ñîñóäîâ, à òàê-

æå ñëó÷àéíûå ìåõàíè÷åñêèå ñîòðÿñåíèÿ). Äëÿ áèîëîãè÷åñêèõ îáúåê-

òîâ ðåçîíàíñ ìîã áû áûòü êðàéíå îïàñåí è âûçûâàòü ñèëüíûå ðàç-

ðóøåíèÿ, îäíàêî êîýôôèöèåíò çàòóõàíèÿ âíóòðåííèõ îðãàíîâ

äîñòàòî÷íî âåëèê, ÷òîáû ýòî íå ïðîèñõîäèëî. Òåì íå ìåíåå ÿâëå-

íèå ðåçîíàíñà â æèâûõ îðãàíèçìàõ íàáëþäàåòñÿ è èíîãäà ïðèâî-

äèò ê âðåäíûì âîçäåéñòâèÿì. Íàïðèìåð, ðåçîíàíñ, ïî-âèäèìîìó,

ÿâëÿåòñÿ îäíîé èç ïðè÷èí âðåäíîãî âîçäåéñòâèÿ èíôðàçâóêà

è âèá-

ðàöèé íà îðãàíèçì.

Ðèñ. 2.3.6. Ðåçîíàíñíûå êðèâûå

×àñòîòà ñîáñòâåííûõ êîëåáàíèé òåëà ÷åëîâåêà â ïîëîæåíèè ëåæà ñîñòàâëÿåò

3...4 Ãö, â ïîëîæåíèè ñòîÿ — 5...12 Ãö; ÷àñòîòà ñîáñòâåííûõ êîëåáàíèé ãðóäíîé

êëåòêè — 5...8 Ãö, áðþøíîé ïîëîñòè — 3...4 Ãö, ÷òî ñîîòâåòñòâóåò èíôðàçâóêîâîìó

äèàïàçîíó.

§ 2.3. Ìåõàíè÷åñêèå êîëåáàíèÿ

§ 2.4. ÓÏÐÓÃÈÅ ÂÎËÍÛ. ÇÂÓÊ

Êîëåáëþùååñÿ òåëî ðàñõîäóåò ÷àñòü ýíåðãèè, âîâëåêàÿ â êîëå-

áàòåëüíîå äâèæåíèå îêðóæàþùóþ óïðóãóþ ñðåäó. Ïðîöåññ ðàñïðî-

ñòðàíåíèÿ êîëåáàíèé â ïðîñòðàíñòâå, ñîïðîâîæäàþùèéñÿ ïåðåíî-

ñîì ýíåðãèè, íàçûâàåòñÿ âîëíîé. Âîëíû, ðàñïðîñòðàíÿþùèåñÿ

â óïðóãîé ñðåäå (òâåðäîé, æèäêîé, ãàçîîáðàçíîé), íàçûâàþòñÿ

ó ï ð ó ã è ì è. Ïðè ýòîì ÷àñòèöû òîé ñðåäû, â êîòîðîé ðàñïðîñò-

ðàíÿåòñÿ âîëíà, íå âîâëåêàþòñÿ â ïîñòóïàòåëüíîå äâèæåíèå, à ëèøü

êîëåáëþòñÿ îêîëî ñâîåãî ïîëîæåíèÿ ðàâíîâåñèÿ. Ïîýòîìó ðàñïðî-

ñòðàíåíèå âîëíû íå ñîïðîâîæäàåòñÿ ïåðåíîñîì âåùåñòâà.

Âîëíîâîé ïðîöåññ õàðàêòåðèçóåòñÿ ôàçîâîé ñêîðîñòüþ (ñêîðîñ-

òüþ ðàñïðîñòðàíåíèÿ âîëíû) v, äëèíîé âîëíû λ, ÷àñòîòîé ν èëè

ïåðèîäîì êîëåáàíèé Ò. Äëèíîé âîëíû íàçûâàåòñÿ ðàññòîÿíèå, íà

êîòîðîå ðàñïðîñòðàíÿåòñÿ âîëíà çà âðåìÿ, ðàâíîå ïåðèîäó êîëåáà-

íèé ÷àñòèö ñðåäû. Î÷åâèäíî, ÷òî

λ= =

òîãäà ôàçîâàÿ ñêîðîñòü âîëíû:

=λν=

. (2.4.1)

Âîëíû ìîãóò áûòü äâóõ òèïîâ: ïîïåðå÷íûå è ïðîäîëüíûå. Ïðè

âîçáóæäåíèè ï î ï å ð å ÷ í û õ âîëí êîëåáàíèÿ ÷àñòèö ïåðïåíäè-

êóëÿðíû íàïðàâëåíèþ ðàñïðîñòðàíåíèÿ âîëíû, à ïðè âîçáóæäå-

íèè ï ð î ä î ë ü í û õ âîëí ñîâïàäàþò ñ íàïðàâëåíèåì ðàñïðîñò-

ðàíåíèÿ âîëíû.

Ãåîìåòðè÷åñêîå ìåñòî âñåõ ÷àñòèö, êîëåáëþùèõñÿ ñ îäèíàêî-

âîé ôàçîé, íàçûâàåòñÿ âîëíîâûì ôðîíòîì. Åñëè âîëíîâîé ôðîíò

ïðåäñòàâëÿåò ñîáîé ïëîñêîñòü, öèëèíäð èëè ñôåðó, âîëíó íàçûâà-

þò ïëîñêîé, öèëèíäðè÷åñêîé èëè ñôåðè÷åñêîé ñîîòâåòñòâåííî.

Âûâåäåì óðàâíåíèå ïëîñêîé âîëíû. Äëÿ ýòîãî íàïðàâèì îñü x âäîëü

íàïðàâëåíèÿ ðàñïðîñòðàíåíèÿ âîëíû. Âñå òî÷êè, ëåæàùèå â êàæäîé ïëîñ-

êîñòè, ïåðïåíäèêóëÿðíîé îñè x, êîëåáëþòñÿ îäèíàêîâî. Âûäåëèì íà îñè x

òî÷êó ñ êîîðäèíàòîé

= 0x (èñòî÷íèê âîëíû). Ïóñòü âñå ÷àñòèöû, íàõîäÿ-

ùèåñÿ â ïëîñêîñòè, ïåðïåíäèêóëÿðíîé îñè x è ïðîõîäÿùåé ÷åðåç òî÷êó

= 0x

, ñîâåðøàþò êîëåáàíèÿ ïî çàêîíó

()

=ω+ϕ

() cosSt A t . (2.4.2)

Âîçáóæäåíèå äîñòèãíåò ïëîñêîñòè ñ ïðîèçâîëüíîé êîîðäèíàòîé x ÷å-

ðåç âðåìÿ

τ= /xv

, ãäå v — ñêîðîñòü ðàñïðîñòðàíåíèÿ âîëíû. Êîëåáàíèÿ

òî÷åê ñ êîîðäèíàòîé x çàïàçäûâàþò è ñîâåðøàþòñÿ ïî çàêîíó

Ãëàâà 2. Ìåõàíèêà