Тиманюк В.А., Животова Е.Н. Биофизика

Подождите немного. Документ загружается.

2.11. Ñêîðîñòü êîëåáëþùåéñÿ òî÷êè:

à) îïåðåæàåò ñìåùåíèå íà π/2;

á) íàõîäèòñÿ â ïðîòèâîôàçå ñìåùåíèþ;

â) îòñòàåò îò ñìåùåíèÿ íà π/2;

ã) ñîâïàäàåò ïî ôàçå ñî ñìåùåíèåì;

ä) èçìåíÿåòñÿ íå ïî ãàðìîíè÷åñêîìó çàêîíó.

2.12. Óðàâíåíèå çàòóõàþùèõ êîëåáàíèé èìååò âèä:

à)

ecos( )

xA t

−ω

=β+ϕ

;ã) =ωω+ϕ

cos( )

xmA t ;

á)

()

=ω+ϕ

cosxA t ;ä) =ω ω+ϕ

cos( )xA t .

â)

ecos( )

xA t

−β

=β+ϕ

;

2.13. Äèôôåðåíöèàëüíîå óðàâíåíèå âûíóæäåííûõ êîëåáàíèé èìååò

âèä:

à) +β +ω =

;ã)

+ω =

;

á)

+ω = ω

cos

xf t

;ä) +β +ω = ω

2cos

xf t

â)

β+ω=

;

2.14. Óðàâíåíèå ïëîñêîé âîëíû èìååò âèä:

à) =ω+ϕ

(,) cos( )Sxt A t ;

á)

(,) e cos

Sxt A t x

−β



=ω−+ϕ





;

â) =ω−π+ϕ

(,) cos( 2 )Sxt A x t ;

ã)



=ω−+ϕ





(,) cosSxt A t x

;

ä)

(,) e cos( )

Sxt A t

−β

=ω+ϕ

2.15. Óðîâåíü èíòåíñèâíîñòè çâóêà èçìåðÿåòñÿ:

à) â ãåðöàõ; ã) âàòòàõ;

á) ôîíàõ; ä) âàòòàõ íà ñåêóíäó â êâàäðàòå.

â) äåöèáåëàõ;

Ïðàêòè÷åñêèå è òåñòîâûå çàäàíèÿ

Ãëàâà 3

ÁÈÎÔÈÇÈÊÀ ÌÛØÅ×ÍÎÃÎ

ÑÎÊÐÀÙÅÍÈß

Â äàííîé ãëàâå ðàññìàòðèâàþòñÿ ìîëåêóëÿðíûå îñíîâû ìû-

øå÷íîãî ñîêðàùåíèÿ è ìåõàíè÷åñêèå ñâîéñòâà ìûøö. Áåç ïîíè-

ìàíèÿ ýòèõ âîïðîñîâ íåâîçìîæíî èçó÷åíèå ìåõàíèçìîâ äåéñòâèÿ

öåëîãî ðÿäà ëåêàðñòâåííûõ ïðåïàðàòîâ: ñïàçìîëèòè÷åñêèõ, à òàê-

æå ïðåïàðàòîâ, ñòèìóëèðóþùèõ ìûøå÷íóþ äåÿòåëüíîñòü, íàïðè-

ìåð ñîêðàùåíèå ñåðäå÷íîé ìûøöû.

Âñå ìûøöû îðãàíèçìà ðàçäåëÿþòñÿ íà ãëàäêèå è ïîïåðå÷íîïî-

ëîñàòûå. Ñðåäè ïîñëåäíèõ ðàçëè÷àþò äâà òèïà: ñêåëåòíûå è ñåð-

äå÷íàÿ. Íèæå áóäóò ðàññìîòðåíû òîëüêî ñêåëåòíûå ìûøöû.

§ 3.1. ÑÒÐÎÅÍÈÅ ÌÛØÅ×ÍÎÃÎ ÂÎËÎÊÍÀ

Ìåìáðàíà ìûøå÷íûõ êëåòîê — ñàðêîëåììà — òàêæå, êàê

è ìåìáðàíà íåðâíûõ êëåòîê, ýëåêòðîâîçáóäèìà è ñïîñîáíà ïðîâî-

äèòü ïîòåíöèàë äåéñòâèÿ. Ýòè ïðîöåññû â ìûøå÷íûõ êëåòêàõ ïðî-

èñõîäÿò ïî òîìó æå ïðèíöèïó, ÷òî è â íåðâíûõ. Ïîòåíöèàë ïîêîÿ

) ìûøå÷íîãî âîëîêíà ñîñòàâëÿåò ïðèáëèçèòåëüíî –90 ìÂ, ÷òî

íèæå òàêîâîãî â íåðâíîì âîëîêíå (–70 ìÂ), à êðèòè÷åñêàÿ äåïî-

ëÿðèçàöèÿ (V

), ïî äîñòèæåíèè êîòîðîé âîçíèêàåò ïîòåíöèàë äåé-

ñòâèÿ, èìååò îäèíàêîâîå çíà÷åíèå ñ íåðâíûì. Ïîýòîìó âîçáóäè-

ìîñòü ìûøå÷íîãî âîëîêíà íåñêîëüêî íèæå, ÷åì íåðâíîãî, òàê êàê

êëåòêó òðåáóåòñÿ äåïîëÿðèçîâàòü íà áîëüøóþ âåëè÷èíó.

∆V

> ∆V

ãäå ∆V = V

– V

, èíäåêñû «ì» è «í» îòíîñÿòñÿ ñîîòâåòñòâåííî

ê ìûøå÷íûì è íåðâíûì êëåòêàì.

Îòâåòîì ìûøå÷íîãî âîëîêíà íà âîçáóæäåíèå ÿâëÿåòñÿ ñîêðà-

ùåíèå, êîòîðîå ñîâåðøàåò ñîêðàòèòåëüíûé àïïàðàò êëåòêè — ìèî-

ôèáðèëëû. Îíè ïðåäñòàâëÿþò ñîáîé òÿæè, ñîñòîÿùèå èç äâóõ âèäîâ

íèòåé: òîëñòûõ — ì è î ç è í î â û õ, è òîíêèõ — à ê ò è í î â û õ.

Òîëñòûå íèòè (äèàìåòðîì 15 íì è äëèíîé 1,5 ìêì) èìåþò â ñâîåì

ñîñòàâå òîëüêî îäèí áåëîê — ìèîçèí; òîíêèå (äèàìåòðîì 7 íì

è äëèíîé 1 ìêì) ñîäåðæàò òðè âèäà áåëêîâ: àêòèí, òðîïîìèîçèí

è òðîïîíèí.

Àêòèí ïðåäñòàâëÿåò ñîáîé äëèííóþ áåëêîâóþ íèòü, îäíàêî åãî

íåëüçÿ îòíåñòè ê ôèáðèëëÿðíûì áåëêàì. Îí ñîñòîèò èç îòäåëüíûõ

ãëîáóëÿðíûõ áåëêîâ, ñöåïëåííûõ ìåæäó ñîáîé òàêèì îáðàçîì, ÷òî

âñÿ ñòðóêòóðà ïðåäñòàâëÿåò ñîáîé âûòÿíóòóþ öåïü. Ìîëåêóëû ãëî-

áóëÿðíîãî àêòèíà (G-àêòèíà) èìåþò áîêîâûå è êîíöåâûå öåíòðû

ñâÿçûâàíèÿ ñ äðóãèìè òàêèìè æå ìîëåêóëàìè. Â ðåçóëüòàòå îíè

îáúåäèíÿþòñÿ òàêèì îáðàçîì, ÷òî îáðàçóþò ñòðóêòóðó, êîòîðóþ

÷àñòî ñðàâíèâàþò ñ äâóìÿ íèòêàìè áóñ, ñîåäèíåííûõ âìåñòå

(ðèñ. 3.1.1). Îáðàçîâàííàÿ èç ìîëåêóë G-àêòèíà ëåíòà çàêðó÷åíà

â ñïèðàëü. Òàêàÿ ñòðóêòóðà

íàçûâàåòñÿ ôèáðèëëÿð-

íûì àêòèíîì (F-àêòè-

íîì). Øàã ñïèðàëè (äëè-

íà âèòêà) ñîñòàâëÿåò

38 íì, íà êàæäûé âèòîê

ñïèðàëè ïðèõîäèòñÿ 7 ïàð

G-àêòèíà. Ïîëèìåðèçà-

öèÿ G-àêòèíà, òî åñòü îá-

ðàçîâàíèå F-àêòèíà, ïðîèñõîäèò çà ñ÷åò ýíåðãèè ÀÒÔ, è, íàîáî-

ðîò, ïðè ðàçðóøåíèè F-àêòèíà âûäåëÿåòñÿ ýíåðãèÿ.

Âäîëü ñïèðàëüíûõ æåëîáêîâ àêòèíîâûõ ôèëàìåíòîâ (íèòåé)

ðàñïîëàãàåòñÿ áåëîê òðîïîìèîçèí (ãðå÷. trope — ïîâîðà÷èâàòü,

mys — ìûøöà). Êàæäàÿ íèòü òðîïîìèîçèíà, èìåþùàÿ äëèíó 41 íì,

ñîñòîèò èç äâóõ èäåíòè÷íûõ α-öåïåé, âìåñòå çàêðó÷åííûõ â ñïè-

ðàëü ñ äëèíîé âèòêà 7 íì. Âäîëü îäíîãî âèòêà F-àêòèíà ðàñïî-

ëîæåíû äâå ìîëåêóëû òðîïîìèîçèíà. Êàæäàÿ òðîïîìèîçèíîâàÿ

ìîëåêóëà ñîåäèíÿåòñÿ, íåìíîãî ïåðåêðûâàÿñü, ñî ñëåäóþùåé, â ðå-

çóëüòàòå òðîïîìèîçèíîâàÿ íèòü ïðîñòèðàåòñÿ âäîëü àêòèíà íåïðå-

ðûâíî (ðèñ. 3.1.2).

Ðèñ. 3.1.1. Îáúåäèíåíèå îòäåëüíûõ ãëîáóë

G-àêòèíà â F-àêòèí

Ðèñ. 3.1.2. Ñòðîåíèå òîíêîé íèòè ìèîôèáðèëëû

Â êëåòêàõ ïîïåðå÷íîïîëîñàòûõ ìûøö â ñîñòàâ òîíêèõ íèòåé

êðîìå àêòèíà è òðîïîìèîçèíà âõîäèò åùå è áåëîê òðîïîíèí. Íà

êàæäûé øàã ñïèðàëè F-àêòèíà ïðèõîäèòñÿ äâå ìîëåêóëû òðîïîíè-

§ 3.1. Ñòðîåíèå ìûøå÷íîãî âîëîêíà

íà. Ýòîò ãëîáóëÿðíûé áåëîê èìååò ñëîæíîå ñòðîåíèå. Îí ñîñòîèò

èç òðåõ ñóáúåäèíèö, êàæäàÿ èç êîòîðûõ âûïîëíÿåò ñâîþ ôóíêöèþ

â ïðîöåññå ñîêðàùåíèÿ.

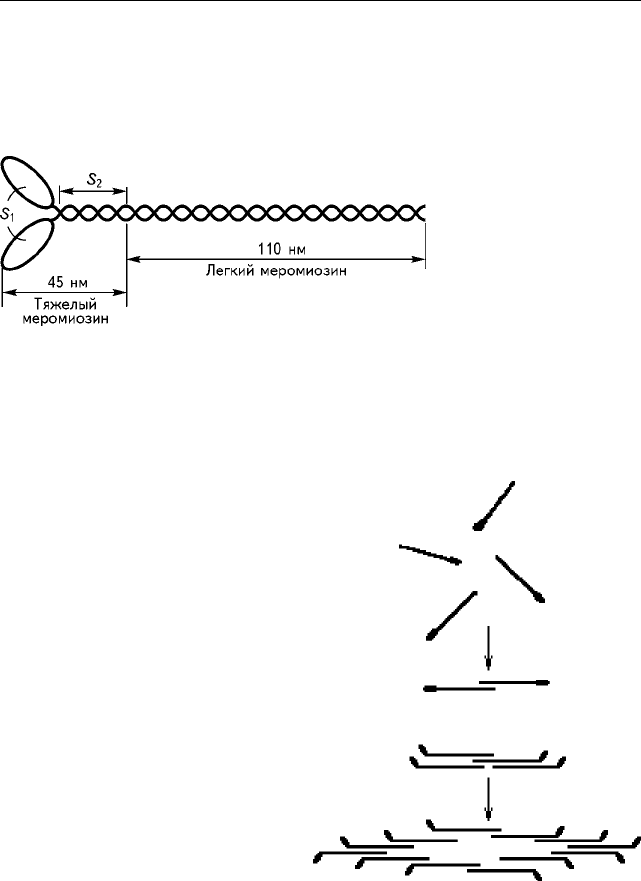
Òîëñòàÿ íèòü ñîñòîèò èç áîëüøîãî ÷èñëà ìîëåêóë ìèîçèíà, ñî-

áðàííûõ â ïó÷îê. Êàæäàÿ ìîëåêóëà ìèîçèíà äëèíîé îêîëî 155 íì

è äèàìåòðîì 2 íì

ñîñòîèò èç øåñòè

ïîëèïåïòèäíûõ íè-

òåé: äâóõ äëèííûõ

è ÷åòûðåõ êîðîòêèõ

(ðèñ. 3.1.3). Äëèí-

íûå öåïè âìåñòå

çàêðó÷åíû â ñïè-

ðàëü ñ øàãîì 7,5 íì

è îáðàçóþò ôèáðèë-

ëÿðíóþ ÷àñòü ìèî-

çèíîâîé ìîëåêóëû. Íà îäíîì èç êîíöîâ ìîëåêóëû ýòè öåïè ðàñêðó-

÷èâàþòñÿ è îáðàçóþò ðàçäâîåííûé êîíåö. Êàæäûé èç ýòèõ êîíöîâ

îáðàçóåò êîìïëåêñ ñ äâóìÿ êîðîòêèìè öåïÿìè, òî åñòü íà êàæäîé

ìîëåêóëå èìåþòñÿ äâå ãîëîâ-

êè. Ýòî ãëîáóëÿðíàÿ ÷àñòü ìè-

îçèíîâîé ìîëåêóëû. Â ìèîçè-

íå âûäåëÿþò äâà ôðàãìåíòà:

ëåãêèé ìåðîìèîçèí (ËÌÌ)

è òÿæåëûé ìåðîìèîçèí (ÒÌÌ),

ìåæäó íèìè íàõîäèòñÿ øàð-

íèð. ÒÌÌ ñîñòîèò èç äâóõ ñóá-

ôðàãìåíòîâ: S

è S

. ËÌÌ

è ôðàãìåíò S

ÒÌÌ âëîæåíû

â ïó÷îê íèòåé, à ñóáôðàãìåíò S

âûñòóïàåò íàä ïîâåðõíîñòüþ.

Ýòîò âûñòóïàþùèé êîíåö (ìè-

îçèíîâàÿ ãîëîâêà) ñïîñîáåí

ñâÿçûâàòüñÿ ñ àêòèâíûì öåíò-

ðîì íà àêòèíîâîé íèòè è èç-

ìåíÿòü óãîë íàêëîíà ê ïó÷êó

ìèîçèíîâûõ íèòåé.

Îáúåäèíåíèå îòäåëüíûõ

ìîëåêóë ìèîçèíà â ïó÷îê

(ðèñ. 3.1.4) ïðîèñõîäèò, ñêî-

ðåå âñåãî, çà ñ÷åò ýëåêòðîñòà-

òè÷åñêèõ âçàèìîäåéñòâèé ìåæäó ËÌÌ. Öåíòðàëüíàÿ ÷àñòü íèòè

(îêîëî 300 íì) íå èìååò ãîëîâîê. Âåñü êîìïëåêñ ìèîçèíîâûõ ìî-

ëåêóë ïðîñòèðàåòñÿ íà 1,5 ìêì. Ýòî îäíà èç ñàìûõ áîëüøèõ áèîëî-

ãè÷åñêèõ ìîëåêóëÿðíûõ ñòðóêòóð, èçâåñòíûõ â ïðèðîäå.

Ðèñ. 3.1.3. Ñòðîåíèå ìîëåêóëû ìèîçèíà

Ðèñ. 3.1.4. Ñõåìà àãðåãàöèè ìîëåêóë ìèî-

çèíà

Ãëàâà 3. Áèîôèçèêà ìûøå÷íîãî ñîêðàùåíèÿ

Ïðè ðàññìàòðèâàíèè

â ïîëÿðèçàöèîííûé ìèêðî-

ñêîï ïðîäîëüíîãî ñðåçà ïî-

ïåðå÷íîïîëîñàòîé ìûøöû

âèäíû ñâåòëûå è òåìíûå ó÷à-

ñòêè. Òåìíûå ó÷àñòêè (äèñ-

êè) ÿâëÿþòñÿ àíèçîòðîïíû-

ìè: â ïîëÿðèçîâàííîì ñâåòå

îíè âûãëÿäÿò ïðîçðà÷íûìè â ïðîäîëüíîì íàïðàâëåíèè è íåïðî-

çðà÷íûìè — â ïîïåðå÷íîì, îáîçíà÷àþòñÿ áóêâîé À. Ñâåòëûå ó÷àñ-

òêè ÿâëÿþòñÿ èçîòðîïíûìè è îáîçíà÷àþòñÿ áóêâîé I (ðèñ. 3.1.5).

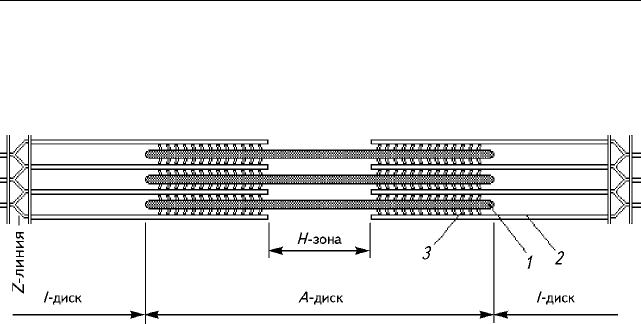
Äèñê I âêëþ÷àåò â ñåáÿ òîëüêî

òîíêèå íèòè, äèñê À — è òîë-

ñòûå, è òîíêèå. Â ñåðåäèíå äèñ-

êà À âèäíà ñâåòëàÿ ïîëîñà, íà-

çûâàåìàÿ Í-çîíîé. Îíà íå èìååò

òîíêèõ íèòåé. Äèñê I ðàçäåëåí

òîíêîé ïîëîñîé Z, êîòîðàÿ ïðåä-

ñòàâëÿåò ñîáîé ìåìáðàíó, ñîäåð-

æàùóþ ñòðóêòóðíûå ýëåìåíòû,

ñêðåïëÿþùèå ìåæäó ñîáîé êîí-

öû òîíêèõ íèòåé. Ó÷àñòîê ìåæ-

äó äâóìÿ Z-ëèíèÿìè íàçûâàåòñÿ

ñàðêîìåðîì.

Êàæäàÿ òîëñòàÿ íèòü îêðóæå-

íà øåñòüþ òîíêèìè, à êàæäàÿ

òîíêàÿ — òðåìÿ òîëñòûìè. Òà-

êèì îáðàçîì, â ïîïåðå÷íîì ñðå-

çå ìûøå÷íîå âîëîêíî èìååò ïðàâèëüíóþ ãåêñàãîíàëüíóþ ñòðóêòó-

ðó (ðèñ. 3.1.6).

§ 3.2. ÑÎÊÐÀÙÅÍÈÅ ÌÛØÖÛ

Ïðè ñîêðàùåíèè ìûøöû äëèíà àêòèíîâûõ è ìèîçèíîâûõ ôè-

ëàìåíòîâ íå èçìåíÿåòñÿ. Ïðîèñõîäèò ëèøü èõ ñìåùåíèå îòíîñè-

òåëüíî äðóã äðóãà: òîíêèå íèòè çàäâèãàþòñÿ â ïðîìåæóòêè ìåæäó

òîëñòûìè. Ïðè ýòîì äëèíà äèñêà À îñòàåòñÿ íåèçìåííîé, à äèñê I

óêîðà÷èâàåòñÿ, ïîëîñà Í ïî÷òè èñ÷åçàåò. Òàêîå ñêîëüæåíèå îêàçû-

âàåòñÿ âîçìîæíûì áëàãîäàðÿ ñóùåñòâîâàíèþ ïîïåðå÷íûõ ìîñòè-

êîâ (ìèîçèíîâûõ ãîëîâîê) ìåæäó òîëñòûìè è òîíêèìè íèòÿìè.

Ïðè ñîêðàùåíèè âîçìîæíî èçìåíåíèå äëèíû ñàðêîìåðà ïðèáëè-

çèòåëüíî îò 2,5 äî 1,7 ìêì.

Ðèñ. 3.1.6. Ïîïåðå÷íûé ñðåç ìèîôèá-

ðèëëû:

1 — ìèîçèíîâûå íèòè, 2 — àêòèíîâûå íèòè

Ðèñ. 3.1.5. Ñòðóêòóðà ìèîôèáðèëëû (ïîïå-

ðå÷íûé ñðåç)

§ 3.2. Ñîêðàùåíèå ìûøöû

êîÿùåéñÿ ìûøå÷íîé êëåòêå ýòè öåíòðû ñâÿçûâàíèÿ ïðèêðûòû

ìîëåêóëàìè òðîïîìèîçèíà, ÷òî ïðåïÿòñòâóåò îáðàçîâàíèþ ñâÿçè

ìåæäó òîíêèìè è òîëñòûìè íèòÿìè.

Äëÿ òîãî ÷òîáû àêòèí è ìèîçèí ìîãëè âçàèìîäåéñòâîâàòü, íå-

îáõîäèìî ïðèñóòñòâèå èîíîâ êàëüöèÿ. Â ïîêîå îíè íàõîäÿòñÿ â ñàð-

êîïëàçìàòè÷åñêîì ðåòèêóëóìå. Ýòà îðãàíåëëà ïðåäñòàâëÿåò ñîáîé

îãðàíè÷åííûå ìåìáðàíàìè ïîëîñòè, ñîäåðæàùèå êàëüöèåâûé íà-

ñîñ, êîòîðûé çà ñ÷åò ýíåðãèè ÀÒÔ òðàíñïîðòèðóåò èîíû êàëüöèÿ

âíóòðü ñàðêîïëàçìàòè÷åñêîãî ðåòèêóëóìà. Åãî âíóòðåííÿÿ ïîâåðõ-

íîñòü ñîäåðæèò áåëêè, ñïîñîáíûå ñâÿçûâàòü Ñà

, ÷òî íåñêîëüêî

óìåíüøàåò ðàçíîñòü êîíöåíòðàöèé ýòèõ èîíîâ ìåæäó öèòîïëàç-

ìîé è ïîëîñòüþ ñàðêîïëàçìàòè÷åñêîãî ðåòèêóëóìà. Ðàñïðîñòðàíÿ-

þùèéñÿ ïî êëåòî÷íîé ìåìáðàíå ïîòåíöèàë äåéñòâèÿ àêòèâèðóåò

áëèçêî ðàñïîëîæåííóþ ê ïîâåðõíîñòè êëåòêè ìåìáðàíó ñàðêî-

ïëàçìàòè÷åñêîãî ðåòèêóëóìà è âûçûâàåò âûõîä Ñà

â öèòîïëàçìó.

Ìîëåêóëà òðîïîíèíà îáëàäàåò âûñîêèì ñðîäñòâîì ê êàëüöèþ.

Ïîä åãî âëèÿíèåì îíà èçìåíÿåò ïîëîæåíèå òðîïîìèîçèíîâîé íèòè

íà àêòèíîâîé òàêèì îáðàçîì, ÷òî îòêðûâàåòñÿ àêòèâíûé öåíòð,

ðàíåå ïðèêðûòûé òðîïîìèîçèíîì. Ê îòêðûâøåìóñÿ àêòèâíîìó

öåíòðó òåïåðü ìîæåò ïðèñîåäèíèòüñÿ ïîïåðå÷íûé ìîñòèê. Ýòî

ïðèâîäèò ê âçàèìîäåéñòâèþ àêòèíà ñ ìèîçèíîì (ðèñ. 3.2.2, à, á).

Ïîñëå îáðàçîâàíèÿ ñâÿçè ìèîçèíîâàÿ ãîëîâêà, ðàíåå ðàñïîëîæåí-

íàÿ ïî÷òè ïîä ïðÿìûì óãëîì ê íèòÿì, íàêëîíÿåòñÿ è ïðîòàñêèâà-

åò àêòèíîâóþ íèòü îòíîñèòåëüíî ìèîçèíîâîé ïðèáëèçèòåëüíî íà

10 íì (ðèñ. 3.2.2, â).

Îáðàçîâàâøèéñÿ àêòèí-ìèîçèíîâûé êîìïëåêñ ïðåïÿòñòâóåò

äàëüíåéøåìó ñêîëüæåíèþ íèòåé îòíîñèòåëüíî äðóã äðóãà, ïîýòî-

Ðèñ. 3.2.1. Ñòðîåíèå ïîïåðå÷íîïîëîñàòîé ìûøöû (ïðîäîëüíûé ñðåç):

1 — òîëñòàÿ (ìèîçèíîâàÿ) íèòü; 2 — òîíêàÿ (àêòèíîâàÿ) íèòü; 3 — ïîïåðå÷íûå ìîñòèêè, îáåñ-

ïå÷èâàþùèå ñâÿçü ìåæäó àêòèíîâûìè è ìèîçèíîâûìè íèòÿìè

Êàê óæå óêàçûâàëîñü, ìèîçèíîâàÿ íèòü èìååò íà ñåáå ìíîæå-

ñòâî ãîëîâîê, êîòîðûìè îíà ìîæåò ñâÿçûâàòüñÿ ñ àêòèíîì. Àêòè-

íîâàÿ æå íèòü, â ñâîþ î÷åðåäü, èìååò ó÷àñòêè (àêòèâíûå öåíòðû),

ê êîòîðûì ìîãóò ïðèêðåïëÿòüñÿ ãîëîâêè ìèîçèíà (ðèñ. 3.2.1). Â ïî-

Ãëàâà 3. Áèîôèçèêà ìûøå÷íîãî ñîêðàùåíèÿ

ìó íåîáõîäèìî åãî ðàçúåäèíåíèå. Ýòî âîçìîæíî òîëüêî çà ñ÷åò

ýíåðãèè ÀÒÔ. Ìèîçèí îáëàäàåò ÀÒÔ-àçíîé àêòèâíîñòüþ, òî åñòü

ñïîñîáåí âûçûâàòü ãèäðîëèç ÀÒÔ. Âûäåëÿþùàÿñÿ ïðè ýòîì ýíåð-

ãèÿ ðàçðûâàåò ñâÿçü ìåæäó àêòèíîì è ìèîçèíîì (ðèñ. 3.2.2, ã),

è ìèîçèíîâàÿ ãîëîâêà ñïîñîáíà âçàèìîäåéñòâîâàòü ñ íîâûì ó÷àñò-

êîì ìîëåêóëû àêòèíà. Ðàáîòà ìîñòèêîâ ñèíõðîíèçèðîâàíà òàêèì

2 3

Ðèñ. 3.2.2. Ñîêðàùåíèå ñàðêîìåðà:

1 — ìèîçèíîâàÿ íèòü; 2 — àêòèâíûé öåíòð; 3 — àêòèíîâàÿ íèòü; 4 — ìèîçèíîâàÿ ãîëîâêà;

5 — Z-ëèíèÿ;

à — âçàèìîäåéñòâèå ìåæäó òîíêèìè è òîëñòûìè íèòÿìè îòñóòñòâóåò; á — â ïðèñóòñòâèè Ñà

ìèîçèíîâàÿ ãîëîâêà ñâÿçûâàåòñÿ ñ àêòèâíûì öåíòðîì íà àêòèíîâîé íèòè; â — ïîïåðå÷íûå

ìîñòèêè íàêëîíÿþòñÿ è ïðîòàñêèâàþò òîíêóþ íèòü îòíîñèòåëüíî òîëñòîé, âñëåäñòâèå ÷åãî

äëèíà ñàðêîìåðà óìåíüøàåòñÿ; ã — ñâÿçè ìåæäó íèòÿìè ðàçðûâàþòñÿ çà ñ÷åò ýíåðãèè ÀÒÔ,

ìèîçíîâûå ãîëîâêè ãîòîâû âçàèìîäåéñòâîâàòü ñ íîâûìè àêòèâíûìè öåíòðàìè

§ 3.2. Ñîêðàùåíèå ìûøöû

îáðàçîì, ÷òî ñâÿçûâàíèå, íàêëîí è ðàçðûâ âñåõ ìîñòèêîâ îäíîé

íèòè ïðîèñõîäèò îäíîâðåìåííî.

Ïðè ðàññëàáëåíèè ìûøöû àêòèâèçèðóåòñÿ ðàáîòà êàëüöèåâîãî

íàñîñà, ÷òî ïîíèæàåò êîíöåíòðàöèþ Ñà

â öèòîïëàçìå; ñëåäîâà-

òåëüíî, ñâÿçè ìåæäó òîíêèìè è òîëñòûìè íèòÿìè óæå íå ìîãóò

îáðàçîâûâàòüñÿ. Â ýòèõ óñëîâèÿõ ïðè ðàñòÿæåíèè ìûøöû íèòè

áåñïðåïÿòñòâåííî ñêîëüçÿò îòíîñèòåëüíî äðóã äðóãà. Îäíàêî òàêàÿ

ðàñòÿæèìîñòü âîçìîæíà òîëüêî â ïðèñóòñòâèè ÀÒÔ. Åñëè â êëåòêå

îòñóòñòâóåò ÀÒÔ, òî àêòèí-ìèîçèíîâûé êîìïëåêñ íå ìîæåò ðàçî-

ðâàòüñÿ. Íèòè îñòàþòñÿ æåñòêî ñöåïëåííûìè ìåæäó ñîáîé. Ýòî

ÿâëåíèå íàáëþäàåòñÿ ïðè òðóïíîì îêî÷åíåíèè.

Ñóùåñòâóåò äâà ðåæèìà ñîêðàùåíèÿ ìûøöû: èçîòîíè÷åñêîå

(èçìåíÿåòñÿ äëèíà âîëîêíà, à íàïðÿæåíèå îñòàåòñÿ íåèçìåííûì)

è èçîìåòðè÷åñêîå (êîíöû ìûøöû íåïîäâèæíî çàêðåïëåíû, âñëåä-

ñòâèå ÷åãî èçìåíÿåòñÿ íå äëèíà, à íàïðÿæåíèå).

§ 3.3. ÌÎÙÍÎÑÒÜ È ÑÊÎÐÎÑÒÜ ÑÎÊÐÀÙÅÍÈß ÌÛØÖÛ

Âàæíûìè õàðàêòåðèñòèêàìè ðàáîòû ìûøöû ÿâëÿþòñÿ ñèëà

è ñêîðîñòü ñîêðàùåíèÿ. Óðàâíåíèÿ, âûðàæàþùèå ýòè õàðàêòåðèñ-

òèêè, áûëè ýìïèðè÷åñêè ïîëó÷åíû À. Õèëëîì è âïîñëåäñòâèè ïîä-

òâåðæäåíû êèíåòè÷åñêîé òåîðèåé ìûøå÷íîãî ñîêðàùåíèÿ (ìîäåëü

Äåùåðåâñêîãî).

Ó ð à â í å í è å Õ è ë ë à, ñâÿçûâàþùåå ìåæäó ñîáîé ñèëó è ñêî-

ðîñòü ñîêðàùåíèÿ ìûøöû, èìååò ñëåäóþùèé âèä:

0max

()()( )( )Pavb P abav b

++=+= +

, (3.3.1)

ãäå v — ñêîðîñòü óêîðî÷åíèÿ ìûø-

öû; Ð — ìûøå÷íàÿ ñèëà èëè ïðèëî-

æåííàÿ ê íåé íàãðóçêà (âíåøíÿÿ

ñèëà, äåéñòâóþùàÿ íà ìûøöó);

max

— ìàêñèìàëüíàÿ ñêîðîñòü óêî-

ðî÷åíèÿ ìûøöû (v = v

max

ïðè P = 0);

— ñèëà, ðàçâèâàåìàÿ ìûøöåé

â èçîìåòðè÷åñêîì ðåæèìå ñîêðàùå-

íèÿ, òî åñòü ïðè òàêîé íàãðóçêå, ïðè

êîòîðîé íå ïðîèñõîäèò èçìåíåíèå

äëèíû ìûøöû (P = P

ïðè v = 0);

a è b — êîíñòàíòû. Ïðèâåäåííîå

óðàâíåíèå èìååò âèä ãèïåðáîëû

(ðèñ. 3.3.1).

Ðèñ. 3.3.1. Çàâèñèìîñòü îòíîñè-

òåëüíîé ñêîðîñòè óêîðî÷åíèÿ

ìûøöû îò îòíîñèòåëüíîé ñèëû

Ãëàâà 3. Áèîôèçèêà ìûøå÷íîãî ñîêðàùåíèÿ

Ïðè ñîêðàùåíèè çà âðåìÿ t ìûøöà ñîâåðøàåò ðàáîòó À:

APvt

. (3.3.2)

Âûðàçèâ v èç óðàâíåíèÿ Õèëëà (3.3.1), ïîëó÷àåì:

AbP t

−

. (3.3.3)

Â ïðîöåññå ñîêðàùåíèÿ ìûøöû âûäåëÿåòñÿ íåêîòîðîå êîëè÷å-

ñòâî òåïëîòû Q. Ýòà âåëè÷èíà íàçûâàåòñÿ òåïëîïðîäóêöèåé. Êàê

ïîêàçàë Õèëë, òåïëîïðîäóêöèÿ çàâèñèò òîëüêî îò èçìåíåíèÿ äëè-

íû õ ìûøöû è íå çàâèñèò îò íàãðóçêè Ð:

Qax=

. (3.3.4)

Îáùàÿ ìîùíîñòü N



, ðàçâèâàåìàÿ ìûøöåé, îïðåäåëÿåòñÿ

ñêîðîñòÿìè âûïîëíåíèÿ ìûøöåé ðàáîòû è âûäåëåíèÿ òåïëîòû:

dd d

AQ Q

NPv

tt t

=+=+



. (3.3.5)

Ïîäñòàâèâ âûðàæåíèå (3.3.4) â (3.3.5), ïîëó÷àåì ñëåäóþùåå:

()

NPva Pav

=+ =+



, (3.3.6)

èëè, êàê ñëåäóåò èç óðàâíåíèÿ Õèëëà,

=+ =

общ

()NPav

=−

()bP P , (3.3.7)

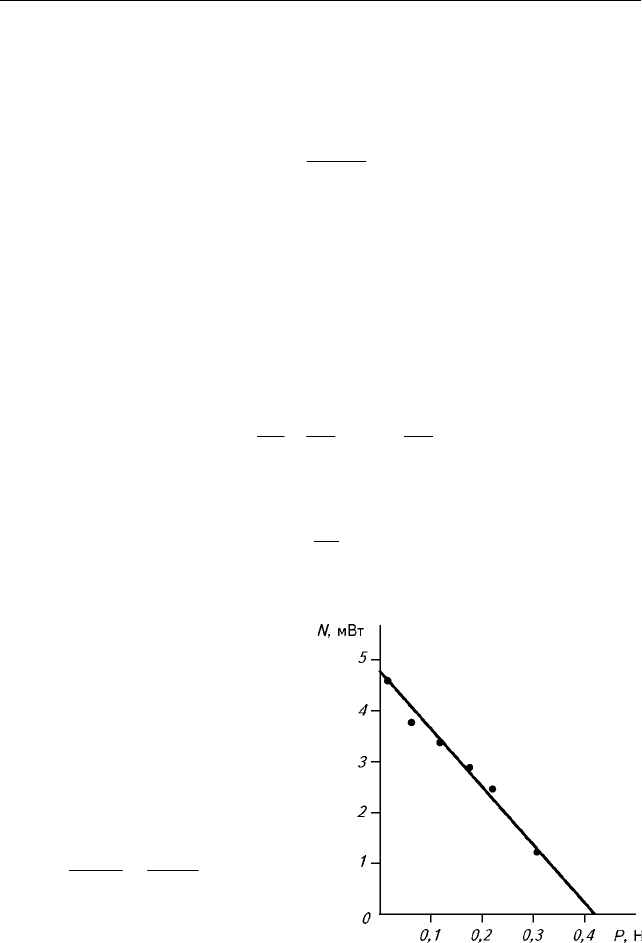
òî åñòü çàâèñèìîñòü ìîùíîñ-

òè N



îò íàãðóçêè P ÿâëÿ-

åòñÿ ëèíåéíîé (ðèñ. 3.3.2).

Êîýôôèöèåíò ïîëåçíîãî

äåéñòâèÿ ìûøöû η çàïèñûâà-

åòñÿ â âèäå:

η= =

общ

APv

AQ N

, (3.3.8)

ãäå

Pv N



— ïîëåçíàÿ ìîù-

íîñòü. ÊÏÄ ìûøöû η ñîõðà-

íÿåò ïîñòîÿííîå çíà÷åíèå

(îêîëî 40 %) â äèàïàçîíå çíà-

÷åíèé ñèëû îò 0,2Ð

äî 0,8Ð

Ðèñ. 3.3.2. Çàâèñèìîñòü ñóììàðíîé ìîù-

íîñòè ïîðòíÿæíîé ìûøöû ëÿãóøêè îò

íàãðóçêè ïðè òåòàíè÷åñêîì èçîòîíè÷å-

ñêîì ñîêðàùåíèè

§ 3.3. Ìîùíîñòü è ñêîðîñòü ñîêðàùåíèÿ ìûøöû

Êîíñòàíòû à è b èìåþò ïîñòîÿííûå çíà÷åíèÿ äëÿ äàííîé ìûø-

öû. Êîíñòàíòà à èìååò ðàçìåðíîñòü ñèëû, à b — ñêîðîñòè. Êîí-

ñòàíòà b â çíà÷èòåëüíîé ñòåïåíè çàâèñèò îò òåìïåðàòóðû, íàïðè-

ìåð, ïðè íàãðåâàíèè íà 10 °Ñ âáëèçè 0 °Ñ b óäâàèâàåòñÿ. Êîíñòàíòà à

íàõîäèòñÿ â äèàïàçîíå çíà÷åíèé îò 0,25Ð

äî 0,4Ð

. Ïî ýòèì äàí-

íûì ëåãêî îöåíèòü ìàêñèìàëüíóþ ñêîðîñòü ñîêðàùåíèÿ äëÿ äàí-

íîé ìûøöû. Òàê êàê (ñëåäóåò èç ïîñëåäíåãî ðàâåíñòâà óðàâíåíèÿ

Õèëëà)

max

(3.3.9)

òî, ñëåäîâàòåëüíî, v

max

ïðåâûøàåò êîíñòàíòó b â 2,5—4 ðàçà.

ÏÐÈÌÅÐÛ ÐÅØÅÍÈß ÇÀÄÀ×

Çàäà÷à 3.1. Äëÿ íåêîòîðîé ìûøöû ïðè íàãðóçêå P = 0,3 Í ñêîðîñòü

ñîêðàùåíèÿ ñîñòàâëÿåò v = 24 ìì/ñ. Íàãðóçêà â èçîìåòðè÷åñêîì ðåæèìå

ñîêðàùåíèÿ ðàâíà P

= 1,1 Í, ïîñòîÿííàÿ à ðàâíà 0,2 Í. Âû÷èñëèòå ìàê-

ñèìàëüíóþ ñêîðîñòü v

max

ñîêðàùåíèÿ.

Ðåøåíèå. Çàïèøåì óðàâíåíèå Õèëëà:

0max

()()( )( )Pavb P abav b++=+= +.

Èç ïîñëåäíåãî ðàâåíñòâà íàéäåì v

max

à èç ïåðâîãî — êîíñòàíòó b:

()vP a

−

Òîãäà

max

()

vP a

PPa

−

Ïîäñòàâèâ ÷èñëîâûå äàííûå (â åäèíèöàõ ÑÈ v = 24•10

–3

ì/ñ), ïîëó÷àåì:

max

24 10 (0,3 0,2) 1,1

82,5 10 м/с 82,5 мм/с.

1,1 0, 3 0, 2

−

⋅⋅+

=⋅=⋅=

−

Çàäà÷à 3.2. Ìûøöà, ñîêðàùàÿñü ñî ñêîðîñòüþ v = 6 ìì/ñ, ðàçâèâàåò

îáùóþ ìîùíîñòü N

îáù

= 2,7 ìÂò. Íàãðóçêà â èçîìåòðè÷åñêîì ðåæèìå ñî-

êðàùåíèÿ äëÿ ýòîé ìûøöû ñîñòàâëÿåò P

= 0,8 Í, êîíñòàíòà b ðàâíà

23 ìì/ñ. Âû÷èñëèòe ðàáîòó A, ïðîèçâåäåííóþ ìûøöåé çà t = 0,5 ñ.

ÏÐÀÊÒÈ×ÅÑÊÈÅ È ÒÅÑÒÎÂÛÅ ÇÀÄÀÍÈß

Ãëàâà 3. Áèîôèçèêà ìûøå÷íîãî ñîêðàùåíèÿ