Тиманюк В.А., Животова Е.Н. Биофизика
Подождите немного. Документ загружается.


31
Âðåìÿ ïîëóâûâåäåíèÿ ïðåïàðàòà:
−
== =
1/2
1
ln 2 0,693
7, 5 ч.
0, 092 ч
el
t
k
Çàäà÷à 1.2. Ïàöèåíòó áûëî ââåäåíî âíóòðèìûøå÷íî M
0
= 220 ìêã ïðå-
ïàðàòà. Âû÷èñëèòå:
à) êîíöåíòðàöèþ c ïðåïàðàòà â êðîâè ÷åðåç t = 3 ÷ ïîñëå ââåäåíèÿ;
á) ñêîðîñòü åãî âûâåäåíèÿ v ÷åðåç t = 3 ÷ ïîñëå ââåäåíèÿ;
â) âðåìÿ t
max
, ïî èñòå÷åíèè êîòîðîãî êîíöåíòðàöèÿ ïðåïàðàòà â êðîâè
äîñòèãíåò ìàêñèìàëüíîãî çíà÷åíèÿ;
ã) ìàêñèìàëüíóþ êîíöåíòðàöèþ c
max
;
ä) ìàêñèìàëüíóþ ñêîðîñòü âûâåäåíèÿ v
max
.
Êîíñòàíòû âñàñûâàíèÿ è âûâåäåíèÿ ðàâíû ñîîòâåòñòâåííî k
in
= 2 ÷
–1
è k
el
= 0,5 ÷
–1
. Êàæóùèéñÿ îáúåì êðîâè ïðèíÿòü ðàâíûì V = 4,5 ë.
Ðåøåíèå. Òàê êàê ïðåïàðàò ââîäèòñÿ íå íåïîñðåäñòâåííî â êðîâü,
à â äðóãóþ òêàíü, òî äàííûé ïðîöåññ áóäåò îïèñûâàòüñÿ îäíîêàìåðíîé
ìîäåëüþ ñ ïîäêàìåðîé. Êîíöåíòðàöèÿ ïðåïàðàòà â îñíîâíîé êàìåðå â ïðî-
èçâîëüíûé ìîìåíò âðåìåíè ñîñòàâëÿåò:
−−
=−=
−
0
() (e e )
()
el in
kt kt
in
in el
Mk
ct
Vk k
=
))
1
11
11
220 мкг 2 ч
exp(0,5 ч3 чexp(2 ч3 ч 14,4 мкг/л.
4, 5 л (2 ч 0, 5 ч )
−
−−
−−
⋅
−⋅−−⋅=
−
Ñêîðîñòü âûâåäåíèÿ ïðåïàðàòà ðàâíà ïåðâîé ïðîèçâîäíîé êîíöåíò-
ðàöèè ïî âðåìåíè
()
0
d
ee
d( )
el in
kt kt
in
el in
in el
cMk
kk
tVk k
−−
=−+
−
. (1.1)
Çíàê «–» óêàçûâàåò íà òî, ÷òî êîíöåíòðàöèÿ ñî âðåìåíåì óáûâàåò.
×åðåç 3 ÷ ïîñëå ââåäåíèÿ ñêîðîñòü âûâåäåíèÿ ñîñòàâèò:
))
1
1111
11
d 220 мкг 2 ч
0,5 чexp(0,5 ч 3 ч 2 чexp(2 ч 3 ч
d
4, 5 л (2 ч 0, 5 ч )
c
t
−
−−−−
−−
⋅
=−−⋅+−⋅=
−
=− ⋅6,95 мкг/(л ч).
Âðåìÿ äîñòèæåíèÿ ìàêñèìàëüíîé êîíöåíòðàöèè âû÷èñëÿåì ïî óðàâ-
íåíèþ (1.6.7):
1
1
max
11
2 ч
ln
ln
0, 5 ч
0, 92 ч 55 мин.
2 ч 0,5 ч
in
el
in el
k
k
t
kk
−
−
−−
== ==
−
−
Òîãäà ìàêñèìàëüíàÿ êîíöåíòðàöèÿ ñîñòàâèò:
Ïðàêòè÷åñêèå è òåñòîâûå çàäàíèÿ

32
max max
0
max
(e e )
()
el in
kt kt
in
in el
Mk
c
Vk k
−−
=−=
−
=
мкг ч
чч чч
лч ч
1
11
11
220 2
exp ( 0,5 0, 92 ) exp ( 2 0, 92 )
4,5 (2 0,5 )
−
−−
−−
⋅
−⋅ −−⋅ =
−
30,8 мкг/л.=
Îïðåäåëèì ìîìåíò âðåìåíè t *, â êîòîðûé ñêîðîñòü âûâåäåíèÿ äîñòè-
ãàåò ìàêñèìàëüíîãî çíà÷åíèÿ, äëÿ ÷åãî âòîðóþ ïðîèçâîäíóþ êîíöåíòðà-
öèè ïî âðåìåíè ïðèðàâíÿåì íóëþ:
2
**
22
0
2
d
(e e )0
()
d
el in
kt kt
in
el in
in el
cMk
kk
Vk k
t
−−
=−=
−
,
îòêóäà
1
1
11
2 ч
2ln
2ln
0, 5 ч
*
2 ч 0,5 ч
in
el
in el
k
k
t
kk
−
−
−−
==
−
−
= 1,84 ÷.
Ïîäñòàâèâ t* â âûðàæåíèå äëÿ ñêîðîñòè (1.1), ïîëó÷èì:
**
0
d
(e e )
d( )
el in
kt kt
in
el in
in el
cMk
kk
tVk k
−−
=−+=
−
1
11 11
11
220 мкг 2 ч
0,5 ч exp( 0,5 ч 1,84 ч) 2 ч exp( 2 ч 1,84 ч)
4, 5 л (2 ч 0, 5 ч )
−
−− −−
−−
⋅
=−−⋅+−⋅=
−
24, 4 мкг/(л ч).=− ⋅
ÇÀÄÀ×È ÄËß ÑÀÌÎÑÒÎßÒÅËÜÍÎÃÎ ÐÅØÅÍÈß
1.1. Âû÷èñëèòå âðåìÿ ïîëóâûâåäåíèÿ t
1/2
íàëüáóôèíà, åñëè åãî êîíñ-
òàíòà ýëèìèíàöèè ñîñòàâëÿåò k
el
= 0,17 ÷
–1
.
1.2. Âû÷èñëèòå êîíñòàíòó ýëèìèíàöèè k
el
ëþìèíàëà, åñëè åãî âðåìÿ
ïîëóâûâåäåíèÿ ñîñòàâëÿåò t
1/2
= 3 ñóòîê.
1.3. Ïàöèåíòó ââåëè âíóòðèâåííî ïðåïàðàò m
0
= 200 ìêã. Âû÷èñëèòå
ìàññó m ïðåïàðàòà â êðîâè ÷åðåç t = 2 ÷ ïîñëå ââåäåíèÿ. Êîíñòàíòà ýëè-
ìèíàöèè äàííîãî ïðåïàðàòà k
el
= 0,17 ÷
–1
. Ïðîöåññ ýëèìèíàöèè îïèñû-
âàåòñÿ îäíîêàìåðíîé ìîäåëüþ.
1.4. Îïðåäåëèòå âðåìÿ ïîëóâûâåäåíèÿ t
1/2
ïðåïàðàòà, åñëè çà âðåìÿ
t = 3 ÷ íàáëþäåíèÿ çà ïàöèåíòîì êîíöåíòðàöèÿ ïðåïàðàòà â êðîâè óìåíü-
øèëàñü ñ ñ
0
= 100 äî ñ = 30 ìêã/ë. Ïðîöåññ ýëèìèíàöèè îïèñûâàåòñÿ îä-
íîêàìåðíîé ìîäåëüþ.
1.5. Íàéäèòå íà÷àëüíóþ êîíöåíòðàöèþ ñ
0
ïðåïàðàòà â êðîâè, åñëè
÷åðåç âðåìÿ t = 10 ÷ ïîñëå âíóòðèâåííîãî ââåäåíèÿ åãî êîíöåíòðàöèÿ ñî-
ñòàâëÿëà ñ = 30 ìêã/ë. Âðåìÿ ïîëóâûâåäåíèÿ äàííîãî ïðåïàðàòà t
1/2
= 8 ÷.
Ïðîöåññ ýëèìèíàöèè îïèñûâàåòñÿ îäíîêàìåðíîé ìîäåëüþ.
Ãëàâà 1. Ìàòåìàòè÷åñêàÿ áèîôèçèêà
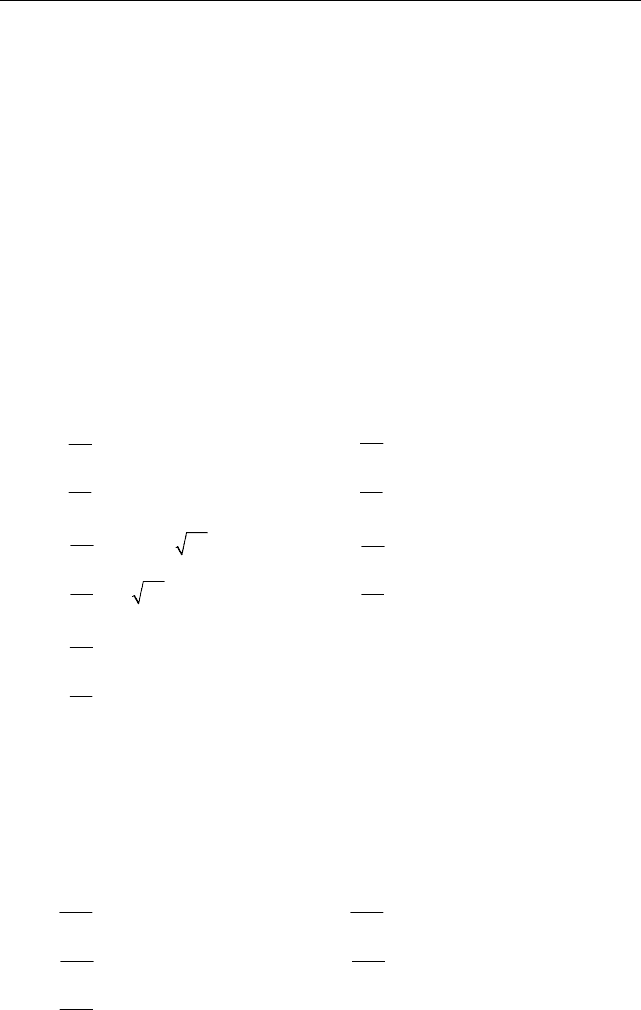
33
1.6. ×åðåç êàêîå âðåìÿ t êîíöåíòðàöèÿ ïðåïàðàòà â êðîâè óìåíüøèòñÿ
â 4 ðàçà, åñëè âðåìÿ ïîëóâûâåäåíèÿ t
1/2
= 6 ÷. Ïðîöåññ ýëèìèíàöèè îïè-
ñûâàåòñÿ îäíîêàìåðíîé ìîäåëüþ.
1.7. ×åðåç êàêîå âðåìÿ t ïîñëå ââåäåíèÿ êîíöåíòðàöèÿ ïðåïàðàòà â êðî-
âè ñîêðàòèòñÿ íà 40 %, åñëè âðåìÿ ïîëóâûâåäåíèÿ ñîñòàâëÿåò t
1/2
= 10 ÷.
Ïðîöåññ ýëèìèíàöèè îïèñûâàåòñÿ îäíîêàìåðíîé ìîäåëüþ.
1.8. Ïàöèåíòó ïîñòàâèëè êàïåëüíèöó è ââîäÿò ïðåïàðàò ñ ïîñòîÿííîé
ñêîðîñòüþ v = 2 ìêã/ìèí. Âû÷èñëèòå ìàññó m ïðåïàðàòà â êðîâè ÷åðåç
âðåìÿ t = 1 ÷, åñëè êîíñòàíòà ýëèìèíàöèè äëÿ íåãî k
el
= 0,25 ÷
–1
.
1.9. Ïàöèåíòó ïîñòàâèëè êàïåëüíèöó è ââîäÿò ïðåïàðàò ñ ïîñòîÿííîé
ñêîðîñòüþ v = 1,5 ìêã/ìèí. Âû÷èñëèòå íàèáîëüøóþ âîçìîæíóþ êîíöåí-
òðàöèþ ñ* ïðåïàðàòà â êðîâè è âåëè÷èíó íàãðóçî÷íîé äîçû Ì
í
, êîòîðóþ
íåîáõîäèìî ââåñòè ïàöèåíòó, ÷òîáû êîíöåíòðàöèÿ ñ* áûëà äîñòèãíóòà
ìãíîâåííî. Êîíñòàíòà ýëèìèíàöèè äàííîãî ïðåïàðàòà k
el
= 0,46 ÷
–1
, êà-
æóùèéñÿ îáúåì êðîâè — V = 4,5 ë.
ÂÎÏÐÎÑÛ ÒÅÑÒÎÂÎÃÎ ÊÎÍÒÐÎËß
1.1. Ìîäåëü «õèùíèê—æåðòâà» îïèñûâàåòñÿ ñëåäóþùåé ñèñòåìîé äèô-
ôåðåíöèàëüíûõ óðàâíåíèé:
à)
=ε +γ
=γ +ε
11
22
d
,
d
d
;
d
x
yxy
t
y
xy y
t
ã)
22
11
22
22
d
,
d
d
;
d
x
yx
t
y
xy
t
=ε −γ
=γ −ε
á)
11
22
d
,
d
d
;
d
x
yxy
t
y
xy x
t
=ε −γ
=γ −ε
ä)
=ε −γ
=γ −ε
11
22
d
,
d
d
.
d
x
xxy
t
y
xy y
t
â)
1
2
d
,
d
d
;
d
x
xy
t
y
xy
t
=γ
=−γ
1.2.  ìîäåëè «õèùíèê–æåðòâà» îñîáûå òî÷êè îòíîñÿòñÿ ê òèïó:
à) «ñåäëî» è íåóñòîé÷èâûé ôîêóñ;
á) óñòîé÷èâûé è íåóñòîé÷èâûé ôîêóñû;
â) óñòîé÷èâûé óçåë è «öåíòð»;
ã) óñòîé÷èâûé è íåóñòîé÷èâûé óçëû;
ä) «öåíòð» è «ñåäëî».
1.3. Â îäíîêàìåðíîé ìîäåëè äèôôåðåíöèàëüíîå óðàâíåíèå, îïèñûâà-
þùåå èçìåíåíèå êîëè÷åñòâà ïðåïàðàòà â êàìåðå, èìååò ñëåäóþùèé âèä:
à)
=−
d
d
el
M
vkM
t
;ã)
=
d
d
in
M
kM
t
;
á)
=−
d
d
el
M
kM
t
;ä)
=−
d
d
in
M
vkM
t
.
â)
′′
=−
d
d
in el
M
kM kM
t
;
Ïðàêòè÷åñêèå è òåñòîâûå çàäàíèÿ

34
1.4. Èçìåíåíèå êîíöåíòðàöèè ïðåïàðàòà â êðîâè â ñëó÷àå îäíîêðàò-
íîãî ââåäåíèÿ îïèñûâàåòñÿ óðàâíåíèåì:
à)
0
() e
el
kt
ct c
−
=+
;ã)
0
() e
el
kt
ct c
−
=
;
á)
0
() e
el
kt
ct c=
;ä)
2
0
() e
el
kt
ct c
−
=
.
â)
0
() e
el
kt
ct c=−
;
1.5. Âðåìÿ ïîëóâûâåäåíèÿ ïðåïàðàòà ñîñòàâëÿåò:
à)
1/2
1
ln
2
el
tk= ;ã)
1/2
2
el
t
k
=
;
á)
1/2
ln 2
el
t
k
=
;ä)
1/2
ln 2
el
tk=
.
â)
1/2
lg 2
el
t
k
=
;
1.6. Ïðåïàðàò ââîäèòñÿ âíóòðèìûøå÷íî, îòêóäà âñàñûâàåòñÿ â êðîâü
ñ êîíñòàíòîé k
1
, à âûâîäèòñÿ èç êðîâåíîñíîãî ðóñëà ñ êîíñòàíòîé k
2
. Ñî-
ñòàâüòå ñèñòåìó äèôôåðåíöèàëüíûõ óðàâíåíèé, îïèñûâàþùèõ êîíöåíò-
ðàöèþ ïðåïàðàòà â ìûøå÷íîé òêàíè (ñ
1
) è êðîâè (ñ
2
):
à)
=−
=−
1
12
2
22 11
d
,
d
d
;
d
c
kc
t
c
kc kc
t
ã)
=−
=+
1
21
2
21 2 11
d
,
d
d
;
d
c
kc
t
c
kc kkc
t
á)
=
=−
1
12
2
22 22
d
,
d
d
;
d
c
kc
t
c
kc kc
t
ä)
=
=+
1
11
2
11 22
d
,
d
d
.
d
c
kc
t
c
kc kc
t
â)
=−
=−
1
11
2
11 2 2
d
,
d
d
;
d
c
kc
t
c
kc kc
t
1.7. Ïðåïàðàò ââîäèòñÿ âíóòðèìûøå÷íî. Åãî êîíöåíòðàöèÿ â êðîâè
â ìîìåíò âðåìåíè t îïèñûâàåòñÿ ñëåäóþùèì óðàâíåíèåì:
à)
0
() (e e )
()
el in
kt kt
in
in el
Mk
ct
Vk k
−−
=−
−
;ã)
0
() (e e )
()
in el
kt kt
el
el in
Mk
ct
kk
=−
−
;
á)
0
() (e e )
()
el in
kt kt
in
el in
Mk
ct
kk
−−
=−
−
;ä)
0
() (e e )
()
el in
kt kt
in
in el
Mk
ct
Vk k
=+
+
.
â)
0
() (e e )
()
in el
kt kt
el
in el
Mk
ct
Vk k
=−
−
;
Ãëàâà 1. Ìàòåìàòè÷åñêàÿ áèîôèçèêà

35
1.8. Ïðåïàðàò ââîäèòñÿ âíóòðèìûøå÷íî. Âðåìÿ äîñòèæåíèÿ åãî ìàê-
ñèìàëüíîé êîíöåíòðàöèè â êðîâè ñîñòàâëÿåò:
à)
=
−
max
ln
el
in
in el
k
k
t
kk
;ã)
=
−
max
ln
in
el
in el
k
k
t
kk
;
á)
−
=
max
ln
in el
in
el
kk
t
k
k
;ä)
−
=
max
ln
el in
in
el
kk
t
k
k
.
â)
=
−
2
max
ln
el
in
el in
k
k
t
kk
;
1.9. Â ìîäåëè íåïðåðûâíîé èíôóçèè äèôôåðåíöèàëüíîå óðàâíåíèå,
îïèñûâàþùåå èçìåíåíèå êîëè÷åñòâà ïðåïàðàòà â êàìåðå, èìååò ñëåäóþ-
ùèé âèä:
à)
=−
d
d
el
M
kM
t
;ã) =
d
d
in
M
kM
t
;
á) =−
d
d
in
M
vkM
t
;ä) =−
d
d
el
M
vkM
t
.
â)
′′
=−
d
d
in el
M
kM kM
t
;
1.10. Â ìîäåëè, îïèñûâàþùåé íåïðåðûâíóþ èíôóçèþ ïðåïàðàòà, ñ òå-
÷åíèåì âðåìåíè åãî êîíöåíòðàöèÿ:
à) óìåíüøàåòñÿ ïî ýêñïîíåíöèàëüíîìó çàêîíó;
á) ëèíåéíî âîçðàñòàåò;
â) îñòàåòñÿ íåèçìåííîé;
ã) âîçðàñòàåò è àñèìïòîòè÷åñêè ïðèáëèæàåòñÿ ê ïîñòîÿííîìó çíà÷å-
íèþ ñ*;
ä) óâåëè÷èâàåòñÿ äî íåêîòîðîãî çíà÷åíèÿ t
max
, à ïîòîì ñíèæàåòñÿ.
1.11. Âûðàæåíèå äëÿ íàãðóçî÷íîé äîçû Ì
í
, ïðè ââåäåíèè êîòîðîé
íåîáõîäèìûé óðîâåíü êîíöåíòðàöèè ñ* ïðåïàðàòà áóäåò äîñòèãíóò ìãíî-
âåííî, èìååò âèä:
à)
∗
=
н
*
el
cVv
M
k
;ã)
∗
=
н
*
el
c
M
Vk
;
á)
∗
=
н
*
el
cV
M
k
;ä)
∗
=
н
*
el
cV
M
vk
.
â)
∗
=
н
*McV;
1.12. Ñêîðîñòü ââåäåíèÿ ïðåïàðàòà, íåîáõîäèìàÿ äëÿ òîãî, ÷òîáû åãî
êîíöåíòðàöèÿ â êðîâè áûëà ïîñòîÿííîé è ðàâíÿëàñü ñ, ñîñòàâëÿåò:
à) v = c
2
Vk
el
;ã) v = cVk
el
k
in
;
á) v = cVk
el
;ä) v = cV
2
k
el
.
â) v = –2cVk
el
;
Ïðàêòè÷åñêèå è òåñòîâûå çàäàíèÿ

Ãëàâà 2
ÌÅÕÀÍÈÊÀ
Ìåõàíèêà çàíèìàåò öåíòðàëüíîå ìåñòî â ôèçèêå è ñâÿçàíà ñî
âñåìè åå ðàçäåëàìè. Ìåõàíèêà èçó÷àåò äâèæåíèå, ðàâíîâåñèå òåë
è ïðîèñõîäÿùèå ìåæäó íèìè âçàèìîäåéñòâèÿ. Îñíîâíûìè ðàçäå-
ëàìè ìåõàíèêè ÿâëÿþòñÿ ñòàòèêà
1
— ó÷åíèå î ðàâíîâåñèè òåë ïîä
äåéñòâèåì ñèë; êèíåìàòèêà — ó÷åíèå î äâèæåíèè òåë áåç ó÷åòà èõ
ìàññ è äåéñòâóþùèõ íà íèõ ñèë; äèíàìèêà — ó÷åíèå î äâèæåíèè
òåë ïîä äåéñòâèåì ïðèëîæåííûõ ê íèì ñèë.
Çíà÷èòåëüíàÿ ÷àñòü ôèçè÷åñêèõ ÿâëåíèé ñâÿçàíà ñ êîëåáàòåëü-
íûìè è âîëíîâûìè ïðîöåññàìè.  ôèçèêå ðàçëè÷àþò ìåõàíè÷åñêèå
è ýëåêòðîìàãíèòíûå êîëåáàíèÿ è âîëíû. Çàêîíû, îïèñûâàþùèå
ìåõàíè÷åñêèå êîëåáàíèÿ è âîëíû, ëåæàò â îñíîâå òàêèõ áèîëîãè÷å-
ñêèõ ïðîöåññîâ, êàê áèåíèå ñåðäöà, ðàñïðîñòðàíåíèå íåðâíîãî
èìïóëüñà è ïóëüñîâîé âîëíû.
§ 2.1. ÊÈÍÅÌÀÒÈÊÀ
Äâèæåíèå êàêîãî-ëèáî òåëà ìîæíî ïðåäñòàâèòü êàê èçìåíåíèå
åãî ïîëîæåíèÿ îòíîñèòåëüíî äðóãîãî, íàçûâàåìîãî òåëîì îòñ÷å-
òà. Ê òåëó îòñ÷åòà ïðèâÿçûâàåòñÿ ñèñòåìà êîîðäèíàò, êîòîðàÿ âìåñòå
ñî ñïîñîáàìè ñîãëàñîâàííîãî èçìåðåíèÿ ïðîìåæóòêîâ âðåìåíè, ðàñ-
ñòîÿíèé è óãëîâ íàçûâàåòñÿ ñèñòåìîé îòñ÷åòà.
Àáñîëþòíî òâåðäûì òåëîì â ìåõàíèêå íàçûâàåòñÿ òåëî, ðàñ-
ñòîÿíèå ìåæäó ëþáûìè äâóìÿ òî÷êàìè êîòîðîãî íå èçìåíÿåòñÿ
â ïðîöåññå äâèæåíèÿ è ïîä äåéñòâèåì ñèë. Ýòî ïîíÿòèå ïðèìå-
íÿåòñÿ è â ñëó÷àå, êîãäà èçìåíåíèåì ðàçìåðîâ è ôîðì òåëà ìîæíî
ïðåíåáðå÷ü.
Åñëè ïðè äâèæåíèè àáñîëþòíî òâåðäîãî òåëà ïðÿìàÿ, ñîåäèíÿ-
þùàÿ ëþáûå äâå òî÷êè, îñòàåòñÿ ïàðàëëåëüíîé ñàìîé ñåáå, òî òà-
1
Ñòàòèêà íå ðàññìàòðèâàåòñÿ â äàííîì ó÷åáíèêå.
37
êîå äâèæåíèå òåëà íàçûâàåòñÿ ï î ñ ò ó ï à ò å ë ü í û ì. Ïðè ïî-
ñòóïàòåëüíîì äâèæåíèè âñå òî÷êè òåëà îïèñûâàþò îäèíàêîâóþ
òðàåêòîðèþ, ïîýòîìó ìîæíî îãðàíè÷èòüñÿ ðàññìîòðåíèåì äâèæå-
íèÿ îäíîé òî÷êè.
Åñëè ïðè äâèæåíèè àáñîëþòíî òâåðäîãî òåëà ïðÿìàÿ, ïðîõîäÿ-
ùàÿ ÷åðåç êàêóþ-ëèáî òî÷êó, îñòàåòñÿ íåïîäâèæíîé, òî òàêîå äâè-
æåíèå íàçûâàåòñÿ â ð à ù å í è å ì òåëà îòíîñèòåëüíî ýòîé ïðÿ-
ìîé — îñè âðàùåíèÿ.
Ëþáîå äâèæåíèå òåëà â êàæäûé
ìîìåíò âðåìåíè ìîæíî ïðåäñòàâèòü
êàê ñóììó ïîñòóïàòåëüíîãî äâèæå-
íèÿ è âðàùåíèÿ îòíîñèòåëüíî îñè,
êîòîðàÿ ìîæåò èçìåíÿòü ñâîå ïîëî-
æåíèå îòíîñèòåëüíî òåëà è ñèñòå-
ìû îòñ÷åòà ñ òå÷åíèåì âðåìåíè.
Äâèæåíèå ìàòåðèàëüíîé òî÷êè
îïðåäåëåíî, åñëè èçâåñòåí çàêîí åå
äâèæåíèÿ, òî åñòü çàêîí, ïî êîòîðî-
ìó èçìåíÿåòñÿ ïîëîæåíèå òî÷êè
â ïðîñòðàíñòâå ñ òå÷åíèåì âðåìåíè.
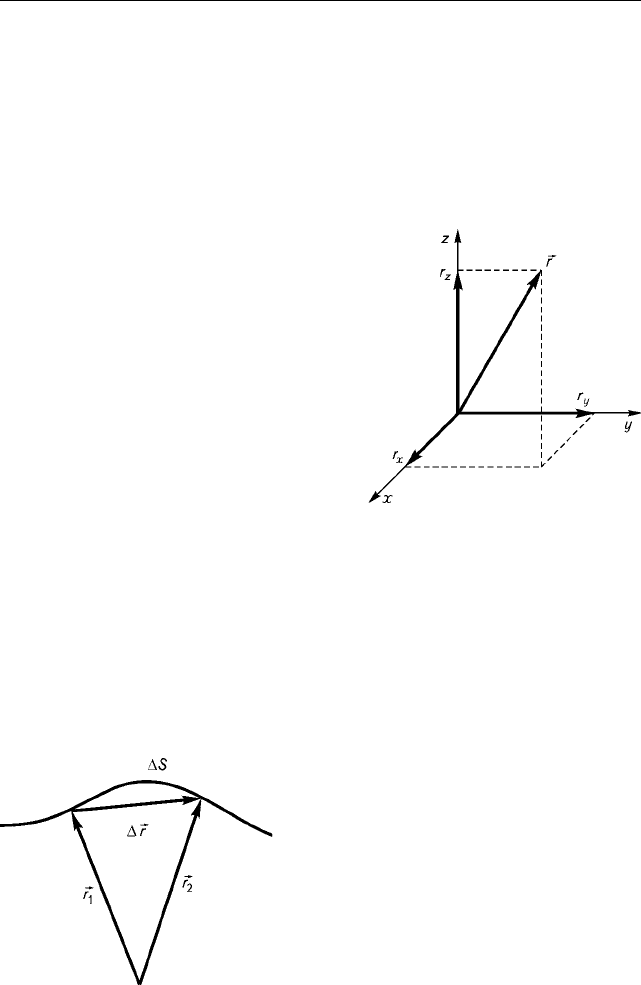
Ïîëîæåíèå òî÷êè â ïðîñòðàí-
ñòâå ìîæåò áûòü çàäàíî ðàäèóñ-âåê-
òîðîì
r
r
, ïðîâåäåííûì îò íà÷àëà
êîîðäèíàò âûáðàííîé ñèñòåìû îò-
ñ÷åòà ê ýòîé òî÷êå (ðèñ. 2.1.1), èëè ïîñðåäñòâîì ïðîåêöèé ,
x
r
,
y
r
z
r
ðàäèóñ-âåêòîðà íà êîîðäèíàòíûå îñè x, y, z. Ýòè ïðîåêöèè îä-
íîâðåìåííî ÿâëÿþòñÿ êîîðäèíàòàìè òî÷êè, òàê ÷òî ,
x
rx
=
,
y
ry=
z
rz=
.
Çàêîí äâèæåíèÿ òî÷êè ìîæíî ïðåäñòàâèòü â âèäå îäíîãî âåê-
òîðíîãî óðàâíåíèÿ:
=
rr
()rrt
(2.1.1)
èëè òðåõ ñêàëÿðíûõ óðàâíåíèé:
===
(); (); ().xxt yyt zzt
(2.1.2)
Ïîñòóïàòåëüíîå äâèæåíèå. Ïóñòü
çà ïðîìåæóòîê âðåìåíè
∆= −
21
tt t
òî÷êà ïåðåìåñòèòñÿ èç ïîëîæåíèÿ,
îïðåäåëÿåìîãî ðàäèóñ-âåêòîðîì
r
1
r
,
â ïîëîæåíèå, îïðåäåëÿåìîå
r
2
r
(ðèñ. 2.1.2).
Âåêòîð
∆= −
rrr
21
rrr
íàçûâàåòñÿ
ïåðåìåùåíèåì òî÷êè. Íåïðåðûâíàÿ
Ðèñ. 2.1.2. Òðàåêòîðèÿ ∆S è ñîîò-
âåòñòâóþùåå ïåðåìåùåíèå ∆
r
r
Ðèñ. 2.1.1. Ðàäèóñ-âåêòîð
r
r
íà
êîîðäèíàòíîé ïëîñêîñòè
§ 2.1. Êèíåìàòèêà

38
ëèíèÿ, îïèñûâàåìàÿ êîíöîì ðàäèóñ-âåêòîðà, íàçûâàåòñÿ òðàåêòî-
ðèåé òî÷êè. Äëèíà ó÷àñòêà ∆S òðàåêòîðèè, ïî êîòîðîé äâèæåòñÿ òî÷-
êà, íàçûâàåòñÿ ïóòåì òî÷êè è ÿâëÿåòñÿ ñêàëÿðîì. Âåëè÷èíû
∆
r
r
è ∆S ñîâïàäàþò ëèøü â ñëó÷àå ïðÿìîëèíåéíîãî äâèæåíèÿ.  ÑÈ
1
ïåðåìåùåíèå è ïóòü èçìåðÿþòñÿ â ìåòðàõ:
[][ ]
мrS
∆=∆ =
r
.
Ñêîðîñòüþ (ëèíåéíîé ñêîðîñòüþ) íàçûâàåòñÿ âåêòîð, íàïðàâ-
ëåííûé â êàæäîé òî÷êå òðàåêòîðèè ïî êàñàòåëüíîé ê íåé è ðàâ-
íûé ïðîèçâîäíîé ðàäèóñ-âåêòîðà ïî âðåìåíè.
 âåêòîðíîé ôîðìå
∆→
∆
==
∆
rr
r
0
d
lim ,
d
t
rr
v
tt
(2.1.3)
â ñêàëÿðíîé ôîðìå
=
d
.
d
S
v
t
(2.1.4)
Åäèíèöà èçìåðåíèÿ ñêîðîñòè — ìåòð â ñåêóíäó:
[]
=v ì/ñ.
Ïðîèçâîäíàÿ ñêîðîñòè ïî âðåìåíè íàçûâàåòñÿ óñêîðåíèåì.
 âåêòîðíîé ôîðìå
∆→
∆
===
∆
rr r
r
2
2
0
dd
lim ,
d
d
t
vv r
a
tt
t
(2.1.5)
â ñêàëÿðíîé ôîðìå
==
2
2
dd
.
d
d
vS
a
t
t
(2.1.6)
Åäèíèöà èçìåðåíèÿ óñêîðåíèÿ — ìåòð â ñåêóíäó â êâàäðà-
òå:
[]
=a ì/ñ
2
.
Åñëè èçâåñòíû çàâèñèìîñòè óñêîðåíèÿ è ñêîðîñòè îò âðåìåíè,
à òàêæå çíà÷åíèÿ ñêîðîñòè è ðàäèóñ-âåêòîðà â íåêîòîðûé ìîìåíò
âðåìåíè
1
t , òî çíà÷åíèÿ ñêîðîñòè è ðàäèóñ-âåêòîðà â ìîìåíò âðå-
ìåíè
2
t îïðåäåëÿþòñÿ ñ ïîìîùüþ èíòåãðàëüíûõ ôîðìóë:
=+
∫
rr r
2
1
21
() () ()d,
t
t
vt vt at t (2.1.7)
2
1
21
() () ()d.
t
t
rt rt vt t
=+
∫
rr r
(2.1.8)
Ãëàâà 2. Ìåõàíèêà
1
Äàëåå åäèíèöû èçìåðåíèÿ âñåõ ââîäèìûõ âåëè÷èí ïðèâåäåíû â ÑÈ áåç
óêàçàíèÿ íà ýòî.
39
Ïóòü, ïðîéäåííûé òåëîì çà ïðîìåæóòîê âðåìåíè
∆= −
21
tt t,
ðàâåí
∆=
∫
2
1
()d.
t
t
Svtt (2.1.9)
Ðàâíîìåðíîå ïðÿìîëèíåéíîå äâèæåíèå îïèñûâàåòñÿ ñëåäóþùèìè
óðàâíåíèÿìè â âåêòîðíîé ôîðìå:
0
0;
const;
,
a
v
rr vt
=
=
−=
r
r
rr r
(2.1.10)
ãäå
0
r
r
— ðàäèóñ-âåêòîð â ìîìåíò âðåìåíè t = 0;
r
r
— ðàäèóñ-
âåêòîð â ïðîèçâîëüíûé ìîìåíò âðåìåíè t.
Ðàâíîïåðåìåííîå ïðÿìîëèíåéíîå äâèæåíèå îïèñûâàåòñÿ ñëåäóþ-
ùèìè óðàâíåíèÿìè â âåêòîðíîé ôîðìå:
=
=+
−= +
r
rr r
rr r r
0
2
00
const;
;
1
,
2
a
vv at
rr vt at
(2.1.11)
ãäå
0
v
r
— âåêòîð ñêîðîñòè â ìîìåíò âðåìåíè t =0;
r
v
— ìãíîâåííîå
çíà÷åíèå ñêîðîñòè â ìîìåíò âðåìåíè t.
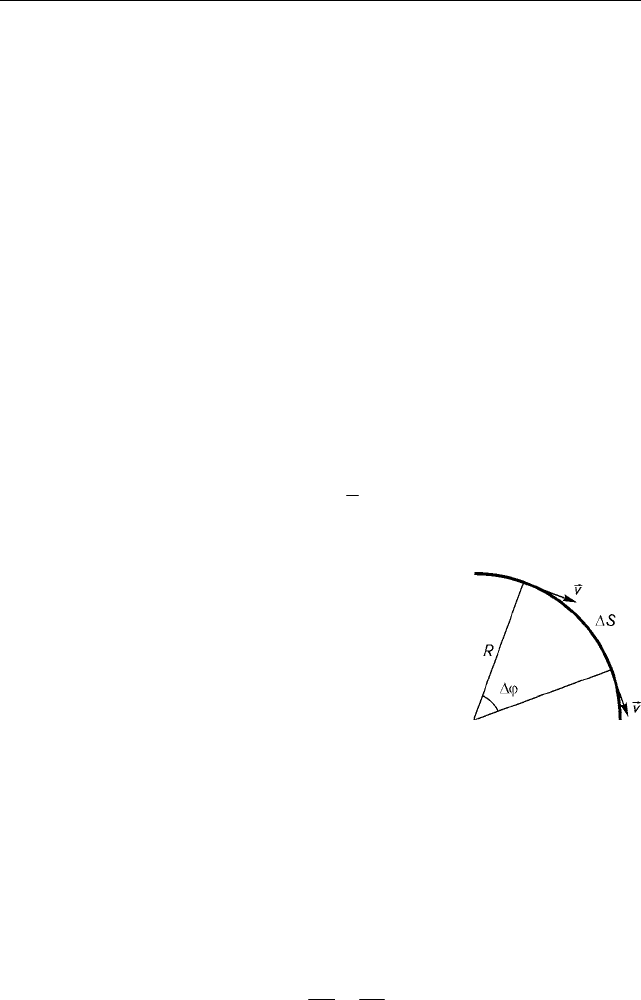
Âðàùàòåëüíîå äâèæåíèå. Ïóñòü òî÷êà âðà-
ùàþùåãîñÿ òåëà îïèñûâàåò äóãó
∆
S
îêðóæíî-
ñòè ðàäèóñà R . Öåíòð îêðóæíîñòè ëåæèò íà îñè
âðàùåíèÿ. Ðàäèóñ-âåêòîð òî÷êè ïðè ýòîì îïè-
ñûâàåò óãîë ∆ϕ (ðèñ. 2.1.3). Çàêîíû âðàùàòåëü-
íîãî äâèæåíèÿ ïðèìåíèìû ê îïèñàíèþ äâè-
æåíèÿ âäîëü ëþáîé ïëîñêîé êðèâîé. Äëÿ ýòîãî
âûáèðàåòñÿ áåñêîíå÷íî ìàëûé åå ó÷àñòîê dS,
íà êîòîðîì ñòðîèòñÿ ñîïðèêàñàþùàÿñÿ îêðóæ-
íîñòü. Åå ðàäèóñ íàçûâàåòñÿ ðàäèóñîì êðèâèçíû äàííîé òî÷êè êðè-
âîé, à öåíòð — öåíòðîì êðèâèçíû. Ðàäèóñ êðèâèçíû îïðåäåëÿåòñÿ
âûðàæåíèåì d'R = dS/dϕ, ãäå dϕ —óãîë, îïèñûâàåìûé ðàäèóñîì-
âåêòîðîì ïðè äâèæåíèè âäîëü êðèâîé íà ó÷àñòêå dS. Ìåæäó äóãîé
∆
S
, ðàäèóñîì R è óãëîì ∆ϕ ñóùåñòâóåò ñîîòíîøåíèå:
∆=∆
ϕ
SR
. (2.1.12)
Ïðîèçâîäíàÿ óãëà ïîâîðîòà ïî âðåìåíè íàçûâàåòñÿ óãëîâîé ñêî-
ðîñòüþ:
∆→
∆ϕ ϕ
ω= =
∆
0
d
lim
d
t
tt
. (2.1.13)
§ 2.1. Êèíåìàòèêà
Ðèñ. 2.1.3. Äâèæåíèå
òî÷êè ïî îêðóæíîñòè

40
Óãëîâàÿ ñêîðîñòü õàðàêòåðèçóåò áûñòðîòó âðàùåíèÿ òåëà. Åäèíè-
öà èçìåðåíèÿ óãëîâîé ñêîðîñòè — ðàäèàí â ñåêóíäó:
[]
ω = ðàä/ñ
2
.
Óãëîâàÿ ñêîðîñòü ñâÿçàíà ñ ëèíåéíîé ñëåäóþùèì ñîîòíîøå-
íèåì:
∆→ ∆→ ∆→
∆∆ϕ∆ϕϕ
== = ==ω
∆∆∆
00 0
d
lim lim lim .
d
tt t
S
vRRRR
tttt
(2.1.14)
Óãëîâàÿ ñêîðîñòü ÿâëÿåòñÿ ïñåâäîâåêòî-
ðîì, íàïðàâëåíèå êîòîðîãî çàâèñèò îò íà-
ïðàâëåíèÿ âðàùåíèÿ è îïðåäåëÿåòñÿ ïî
ïðàâèëó ïðàâîãî âèíòà (ðèñ. 2.1.4).
Áûñòðîòà èçìåíåíèÿ óãëîâîé ñêîðîñòè
õàðàêòåðèçóåòñÿ óãëîâûì óñêîðåíèåì:
∆→
∆ω ω ϕ
ε= = =
∆
2
2
0
dd
lim .
d
d
t
tt
t
(2.1.15)
Åäèíèöà èçìåðåíèÿ óãëîâîãî óñêîðåíèÿ —
ðàäèàí â ñåêóíäó â êâàäðàòå:
[]
ε=ðàä/ñ
2
.
Óãëîâîå óñêîðåíèå òàêæå ÿâëÿåòñÿ ïñåâäîâåêòîðîì, íàïðàâëå-
íèå êîòîðîãî ñîâïàäàåò ñ íàïðàâëåíèåì âåêòîðà óãëîâîé ñêîðîñòè
ïðè óñêîðåííîì äâèæåíèè èëè ïðîòèâîïîëîæíî åé ïðè çàìåäëåí-
íîì.
Ðàâíîìåðíîå âðàùàòåëüíîå äâèæåíèå ñîâåðøàåòñÿ ñ ïîñòîÿííîé
óãëîâîé ñêîðîñòüþ è îïèñûâàåòñÿ ñëåäóþùèìè óðàâíåíèÿìè:
ε=
ω=
ϕ=ϕ +ω
0
0,
const,
,t
(2.1.16)
ãäå
ϕ
0
— íà÷àëüíîå çíà÷åíèå óãëà ïîâîðîòà (ïðè =
0t
).
Ðàâíîïåðåìåííîå âðàùàòåëüíîå äâèæåíèå ñîâåðøàåòñÿ ñ ïîñòî-
ÿííûì óãëîâûì óñêîðåíèåì è îïèñûâàåòñÿ ñëåäóþùèìè óðàâíå-
íèÿìè
ε=
ω=ω +ε
ε
ϕ=ϕ +ω +
0
2
00
const,
,
,
2
t
t
t
(2.1.17)
ãäå
ω
0
— íà÷àëüíàÿ óãëîâàÿ ñêîðîñòü (ïðè
=
0t
).
Âðåìÿ T, â òå÷åíèå êîòîðîãî ñîâåðøàåòñÿ îäèí îáîðîò, íàçû-
âàåòñÿ ïåðèîäîì âðàùåíèÿ. ×àñòîòà âðàùåíèÿ â åäèíèöó âðåìåíè
îáîçíà÷àåòñÿ ν. Î÷åâèäíî, ÷òî
Ðèñ. 2.1.4. Íàïðàâëåíèå
âåêòîðà (ïñåâäîâåêòîðà)
óãëîâîé ñêîðîñòè
Ãëàâà 2. Ìåõàíèêà
