Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§
1.
Числові ряди
181
Заданий ряд збігається, бо задовольняє умовам теореми Лейбніца для
знакопочережних рядів:
Ііт
1
= 0.
УІП
+
1
л/й
п
->~ 4п
Отже, заданий ряд є умовно збіжним.
г) X ^
П +
^
. Заданий ряд є знакопочережним.
и=1
Зп + 2
Складаємо ряд з абсолютних величин членів заданого ряду X
2п +
1
Цей ряд є розбіжним, бо не виконується необхідна умова збіжності:
2п +
]
~2п
Ііт и„
Ііт
2п + \
>Зп
+ 2
Л*0.
З
Зп + \~3п
п
—>
°°
Отже, заданий ряд не є абсолютно збіжним.
Враховуючи, що для заданого ряду також не виконується необхідна
умова збіжності, робимо висновок, що заданий ряд розбіжний. М
Приклад 10. Дослідити на збіжність ряд з комплексними
у 1
членами: > .
£п(3 + і)"
• Розглянемо ряд, складений з модулів членів заданого ряду:
1 , , 1
де
|3 + /| = 7Ї0 ,
тому («„( =
•
и(3 + і)"
1
п\3 + і\
«10^
отже, ХК|
=
Х
и=1 п=\
1
Ряд X-
л=1
1
пЮ
2
збігається за першою ознакою порівняння, бо
и-10
2
1
1

182
Глава 2. Ряди
°° 1 1
а ряд У є геометричним рядом при а = —-тт- < 1, який збігається.
«~ї(іо
І/2
)"
ю
1/2
Отже, заданий ряд У абсолютно збігається. А
Приклад 11. Дослідити на збіжність ряд з комплексними
членами:
^
я(2/-1)"
/7=1 З
• Розглянемо ряд, складений з модулів членів заданого ряду:
/7(2/
-1)" , . п\2і-\\"
и„ = ; \и
п
\ = —
1
—,
П ^
П
І П І З"
де 12/ -11 = V5 , тому |
и„
\
З"
00 00
п-5
2
Отже,
5>»І=£—г
•
п=1 п=1 ->
Звернемося до ознаки Даламбера для дослідження останнього ряду
на збіжність.
Врахуємо, що | м
п+
| |
/і+і
(и + 1)-5
2
2 п+1
/НІ і
т
• ,• К+і
г
2
-3
й
5
2
Тоді Ііт , = Ііт = — <
1
и„ *і-+~ . " З
3"
+1
- п-5
2
Отже, збігається ряд, складений з модулів членів заданого ряду.
Звідси випливає, що заданий ряд ^
л
^' ^ збігається абсолютно.
п=і З
Приклад 12. Дослідити на збіжність ряд з комплексними
членами:

§1.
Числові ряди
183
• Розглянемо ряд, складений з модулів членів заданого ряду:
І
я=1
—і П
Цей ряд розбігається, бо є гармонічним. Тому заданий ряд не є абсо-
лютно збіжним.
Дослідимо заданий ряд на збіжність.
Враховуючи, що / = -1, представимо заданий ряд у вигляді:
V — - ---І І і1_
п ~ ' 2 3
+
4
+
5 6 7
+
8
и=1
/ 1
= х —
1
+•
Д4І
+
1
4к+2 4к
+ 3
4к
+
4
00
( о» о Л °°
= Х = Х(**+*>*)>
^(4А + 1)(4А+3) (4*+2)(4А + 4)
21
^ -2
ДЄ С
* (4* + 1)(4* + 3) ' * (4£ + 2)(4Л: + 4)
2_
(4А + 1К4Л + 3) 8Г
І , і 2 1
'
41
(4* + 1)(4* + 3) 8*
2
Ряди
XI
е
*І'
XI^І збігаються за граничною ознакою порівняння
к=0 к=0
(порівняно з узагальненим і армонічним рядом X
-
Г' Р ~
2 >
''
якии
збіга-
к
ється).'Тому заданий ряд У— збігається.
Враховуючи, що ряд, складений з модулів членів заданого ряду, роз-
бігається, робимо висновок, що заданий ряд умовно збіжний. ^
IV. Задачі для практичних занять
Збіжність числового ряду
У задачах 2.1 - 2.4 для заданого ряду треба:
1) знайти частинну суму 5„; 2) довести збіжність ряду,
користуючись безпосередньо означенням збіжності; 3) знайти
суму 5
і
ряду.

184
Глава
2. Ряди
2.1.
а) У ; б) У .
л=
,л(л + 1)
н
=\п(п + 3)
ОО
1 сю 1
2.2.
а) У --; б) У
(Зп - 2) (Зп +1)
„=,
(2и - 1)(2я + 5)
.
_ . ^ 2/1 +
1
_ ^ п
я
~/і
2
(я + 1)
2
'
„=,(2/7-І)
2
(2/7
+І)
2
'
У задачах 2.5-2.10 довести розбіжність рядів, використо-
вуючи достатню умову розбіжності.
2.5.
£*!±і.
2.6. £-£-.
„=,4/7 + 2 „=,2/7
2
+1
2.7. £соз^. 2.8. £(-1)".
/7 = 1
й
/7 = 1
2.9.
£Г—Т.
2.10. £(/7
2
+2)1п"
2+3
и = 1
«
2
Ряди з додатними членами
У задачах 2.11 - 2.17 дослідити на збіжність задані ряди,
використовуючи ознаки порівняння.
2.11.
а) У—!—; б) У —
т
.
~,3/і-2'
'£,(2/1-І)
2
1 ^ 1
2.12.8)2-5—
7ї
б
) 1-Тт
и=
іи
-4/7 +
5
„
=]
V/?
2
2.13.
а) б) £^
„=,3//
3
-1 „=, 4/7
3
+
2/7
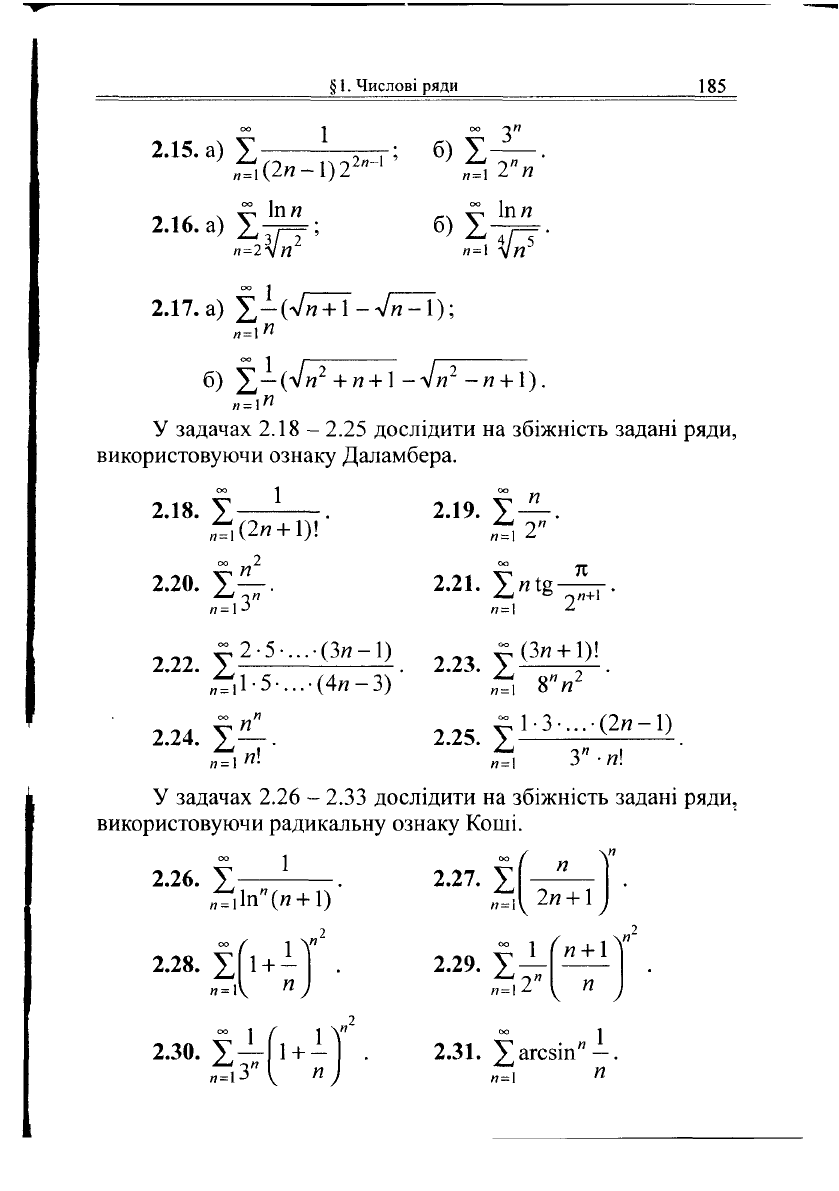
§1.
Числові ряди
185
со
л оо ")Н
2.15. а) У ——; б) У-—
2.16. а) X
1п
п
б) X
1п
п
•
4/ 5
2.17. а)
У-(Л/ПТТ-Л/Л^Т);
б)
Х~"(
Л
/"
2
+ « + 1
—Л/ЛЇ
2
—« +
и = 1
У задачах 2.18 - 2.25 дослідити на збіжність задані ряди,
використовуючи ознаку Даламбера.
2.18. X
1
и
=і(2л + 1)!
2.19.
X
—
и = 1
2.20.
X—
И=1
->
2.21. Х^§-
2
„
+1
•
2.22.
X
2-5-...-(Зл-1)
И
Г,1-5-....(4л-3)
2.24.
2^-.
2.23.
Е
£!±1)!
л = 1
о И
л = 1
2.25. X
л = 1
1-3-...(2и-1)
З" •
п\
У задачах 2.26 - 2.33 дослідити на збіжність задані ряди,
використовуючи радикальну ознаку Коші.
(
2.26.
X—
1
~,гп>
+ 1)
2.27. X
л=1
2и +
1
2.28. X
1 +
її
и =
1\
ОО
1
2.29. У —
п = \
£
П
+
1
чи
V
И
У
2.30.
X—Гі
+ -Т
2.31.
У агсзіп" —.
и=1
«
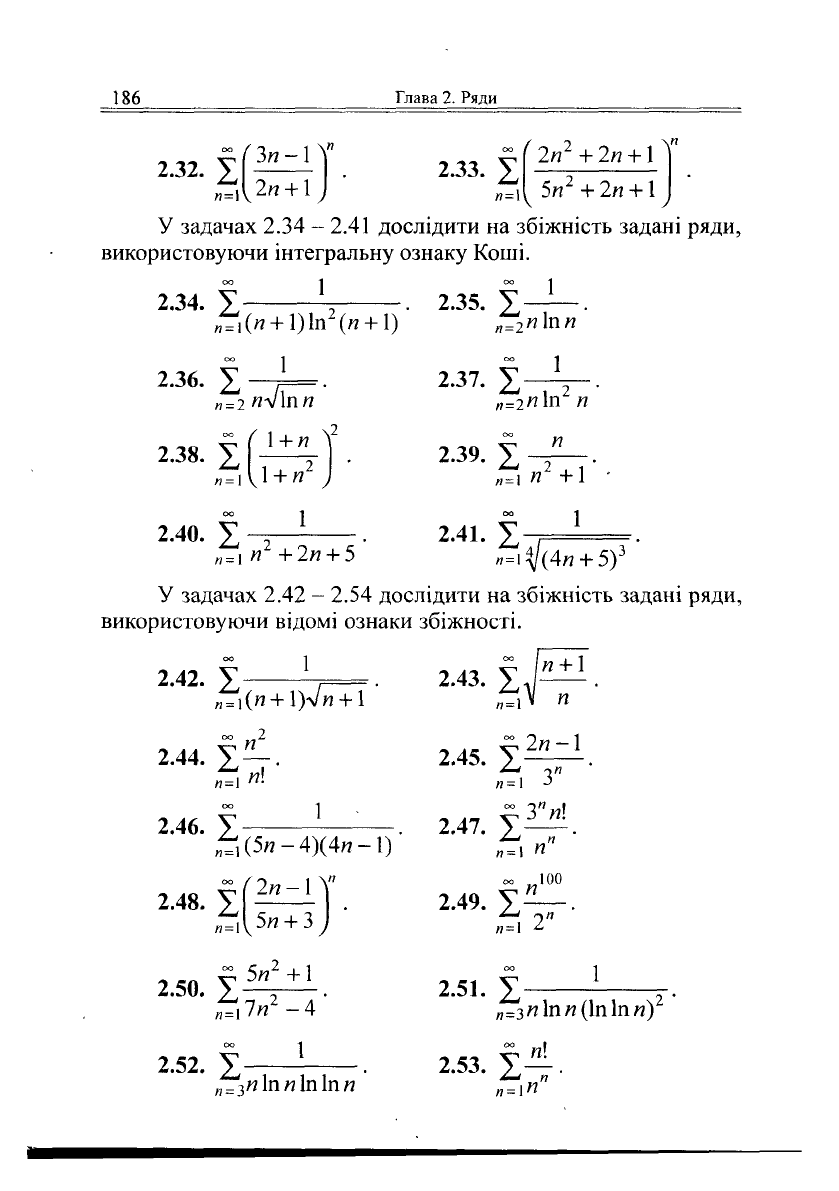
186
Глава 2. Ряди
232
уГ^ІЇ
2.33.
X
/7
=
1
(
2г? +2л +
1
5п
2
+ 2п +
1
У задачах 2.34 - 2.41 дослідити на збіжність задані ряди,
використовуючи інтегральну ознаку Коші.
2.34. X
л
=
1
2.36. £
1
„
= і0?
+ 1)1п
(гс
+ 1)
1
2.35. X
1
„ = 2
ПЛППП
2.37. X
„
=2
л
1п
п
1
2.38. X
л
=
1
1
+ П
\ + п
2
2.39. X
2.40.
X
-5—^
„
=
і и +2и + 5
2-41.
X
„=,
+1
1
«=і^(4«
+ 5)
3
'
У задачах 2.42 - 2.54 дослідити на збіжність задані ряди,
використовуючи відомі ознаки збіжності.
2.42.
X
1
„
=
і(и + 1)л/
2.43.
X
п + \
2.44.
Х^г.
/7
=
1
2.46. X
1
~,(5и-4)(4и-1)
2.48.
Х(^Т
п=
\5п + з)
/7
=
1
2.45. ±=^1.
тл
л
=
1
~>
^
3"
2.47. У — .
л
=
>
и"
ос 100
2.49.
X
—
л
=
1
£
5л
2
+1
2.50. X
2
~,7л
2
-4
2.51.
X
1
2.52.
X
1
„=зл1пи(1п Іпл)
2 •
„
=3
«1п
піп \пп
2-53.
X-
п
=
\П

§
1.
Числові ряди
187
2.54. а) 2 1-- ;
6)2
п=1\
1 +
-
; в) 2
У задачах 2.55 - 2.58 довести, що Ііт и
п
= 0, використо-
вуючиряд
2«„
•
и=1
2.55. и
и
= —.
2.57. и„ =
2.56. и
и
= (а > 1)
,
2.58. и. =
Знакозмінні ряди
У задачах 2.59 - 2.72 дослідити, які з заданих рядів збіга-
ються абсолютно, які збігаються умовно, які розбігаються.
2.59. 2(-1)"
+І
1
Ч
Л+1
1
я=1
Зл-1
2.бі. 2(-і)
п+1 П +
1
и = 1
1
2.бз.
2Н)"4=
и = 1 >/И
2.60. 2(-іГ з
„ = і
(2п-1)
2.62.
±(-\)"-^-.
2.64. 2(-1)" -Ц
„=і /7л/л
2.65. 2
81ПЯСХ
я = 1 «
2.66. 2
зіп «а
2.67.
2НГ
Іпя
я=2
„~(1пЗ)
л
2.68.
У(-1)"
+1
-
и
4г
іп(и + і)
1
2.69.
2(~
1
)"
—
„=3
«1п77(1ПІП/7)"
2.70.
2Н)
2"
я = 1
ПІ

188
Глава 2. Ряди
Ряди
з комплексними членами
У
задачах 2.73 - 2.80 дослідити на збіжність задані ряди з
комплексними
членами.
2.73.
У
„%п\(е-іУ
-т
^ ЗІП/77
2.75.
У .
,1 = 1 ->
2.77.
£<!±£ї.
,7 = 1 /
2.79.
2
,7=1
^2 + /
V
2.74.
2
/
(2л +
і)
*=і\
4л
4,7
(2
+ і)"п
2.76.
У
л=1 ^
2.80.
2
,7 = 1
Л /
5" п
2
+\
§2.
Функціональні ряди. Степеневі ряди
І. Короткі теоретичні відомості
Функціональні ряди
Основні поняття. Ряд вигляду
У>«(Х>.
(2.15)
де и
п
(х) - члени ряду с функціями від х, називається функціональним.
Областю збіжності функціонального ряду (2.15) називається мно-
жина значень аргументу х, для якого цей ряд збігається. Областю збіжності
функціонального ряду найчастіше є який-небудь проміжок осі Ох . Позна-
чимо область збіжності через X .
На практиці для визначення області збіжності функціонального ряду
(2.15) користуються ознакою Даламбера або радикальною ознакою Коші,
тобто, якщо
Ііт
(*)
и
п
(х)
= /(*)
або

§2.
Функціональні ряди. Степеневі ряди
189
Ііт
VI
«„001
='(*).
то для визначення області збіжності слід розв'язати нерівність 1(х) < 1 , а
для визначення області розбіжності - нерівність 1(х)> 1. При цьому для
дослідження поведінки ряду в точках, де 1(х) =
1
(в точках межі області),
проводиться додаткове дослідження (це пов'язано з тим, що вказані ознаки
збіжності при І(х) =
1
не дають відповіді на питання збіжний ряд чи ні).
Сума п перших членів ряду (2.15) називається п -ю частинною су-
мою 5
п
(х) ряду, тобто
я„
(*)=£«*(*).
к = \
Функція
5(х) = Ііт 8
п
(х),
/7_>оо
де х є X , називається сумою ряду.
Функція
г
п
(х) = 8(х)-8„(х) =
к = п+]
називається п - м залишком ряду.
Функціональний ряд (2.15) називається рівномірно збіжним на про-
міжку [а,Ь], якщо для будь-якого Є > 0 існує такий номер N є N , що для
всіх п > N і Ухє[а,Ь] виконується нерівність |/•„ (х) | < є.
Функціональний ряд (2.15) називається мажоровним на проміжку
[а, Ь], якщо існує збіжний числовий ряд з додатними членами
І>„ , (2.16)
»=і
такий, що
|и
я
0с)|<а„
(2.17)
на цьому проміжку.
Збіжний числовий ряд з додатними членами (2.16) називаєтьсямажо-
рантним на проміжку [а, Ь] по відношенню до функціонального ряду (2.15).
Теорема 1 (ознака Вейєрштрасса). Якщо функціональний ряд (2.15)
мажоровний на проміжку [а, Ь], то він абсолютно і рівномірно збіжний на
цьому проміжку.
Теорема 2 (критерій Коші). Для того, щоб функціональний ряд (2.15)
був рівномірно збіжним на [а,Ь], необхідно та достатньо, щоб для будь-
якого є > 0 існував такий номер N , що для всіх п > N і для будь-якого
натурального числа р виконувалась нерівність

190
Глава 2. Ряди
п+р
2>
А
(х)
<Є.
к=п+\
Рівномірно збіжні ряди мають такі властивості.
1°.
Якщо ряд
Х
м
и(
х
),
де функції и„{х) неперервні на відрізку [а, Ь],
л=І
рівномірно збіжний і має суму 8(х) на цьому відрізку, то сума ряду 8(х)
неперервна функція на відрізку [а, Ь].
2°.
Якщо ряд
]Г
м
л(*)>
Д
е
функції и
п
(х) неперервні на відрізку
Л=|
[а, Ь], рівномірно збіжний і має суму 8(х) на цьому відрізку, то
X
X ся оо X
\8(х)ах = \^и
п
(х)сІх= ^и„(х)ах,
а
а"=І
и
= 'а
де (а, х) є [а, Ь\.
3°.
Якщо ряд X и
п
(х), де функції и
п
(х) неперервні та диференційов-
тобто
ні на відрізку [а, Ь], збіжний на цьому відрізку і має суму 8(х), а ряд £
и'„
(х)
я=1
рівномірно збіжний на відрізку [а, Ь] і має суму Р(х), то для всіх х є [а, Ь]
8'(х) = Р(х),
(
» \
Я = 1
)
П = \
Властивості 2° та 3° означають, що при виконанні вказаних умов
функціональні ряди можна почленно інтегрувати та диференціювати.
Степеневі ряди
Основні поняття. Степеневим рядом називається функціональний
ряд вигляду
або
л=0
^а„(х-а)"
,
л=0
(2.18)
(2.19)
де а, а
0
, а
х
, а
2
, ... - дійсні числа.
