Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§3.
Системи диференціальних рівнянь
161
1.354.
сіх
сії
= 2х
+
у,
(Іу
(корені характеристичного
— = Х + Зу~2, .
сії рівняння А, = 2, А,
2
з=3±г)
СІ2.
сії
-х
+ 2у +
32,
Лінійні неоднорідні системи диференціальних
рівнянь зі сталими коефіцієнтами
У задачах 1.355 - 1.363 розв'язати задані лінійні неоднорід-
ні системи диференціальних рівнянь зі сталими коефіцієнтами,
використовуючи: а) метод виключення, б) метод підбору час-
тинного розв'язку за виглядом правої частини; в) метод варіації
довільних сталих.
1.355.
1.357.
сіх
сії
сіу
[сії
сіх
сії
0у_
[сії
У,
х +
е'
+ Є
'.
Зх-2у
+1,
Зх-4у.
1.356.
сіх ,
— = 2у
- 5х
+ е
,
сії
СІУ <- -21
— =
х-6у
+ е
.
[сії
х-у,
1.358.
сіх
сії
сіу І
-^--Х
+ у + е
.
[сії
— = 5х - Зу +
Іе
1.359.
сіх
сії
сіу
сії
2І
1.360.
Зх -
у + е
ЗІ
сіу_
сіх
СІ2
+
2у+4г=\
+ 4х,
З 2
+У-2-—Х
.
сіх 2
1.361.
сіу о
Н 2у + 2
= 81ПХ,
СІХ
^
2
л п
4у - 22 = С08Х.
.сіх

162
Глава
1.
Диференціальні рівняння
1.362.
— - 4х - у + 36/ = О,
сії
1.363.
[сії
сіу
сіх
СІ2
[сіх
х(0) = 0, у(0) = \.
+ 2х- у + 2е' = 0,
+ 3у + 4г = 2х,
-у-2
= Х,
у(0)
= 0, 2(0) = 0.
У задачах 1.364 - 1.366 знайти загальні розв'язки систем
диференціальних рівнянь, використовуючи метод варіації довіль-
них сталих.
1.364.
1.365.
СІХ
сії
сіу
сії
сіх
сії
сіу
сії
х + у- соз/,
:
—2х
- у + зіп І + соз І.
— = у + 1^1-\,
-х +
1§
І.
1.366.
сіу
+ 2 = 1,
сіх
СІ2 2
— +
—
СІХ X
+ — у =
1п
X.
У задачах 1.367 - 1.373 розв'язати вказані системи дифе-
. , СІу , СІ2 .
ренціальних рівнянь (у =—, г = —, якщо не вказано інше).
сіх сіх
1.367.
1.369.
\угу =х,
[у
2
/ = х.
\2
=
у'(2-у)
2
,
[у =
2'(2-у)
2
.
1.368.
1.370.
\ху =у,
\х22' +Х
2
+ у
2
=0.
х + у
у =•
2 — •
2
Х-У
У
§3.
Системи диференціальних рівнянь
163
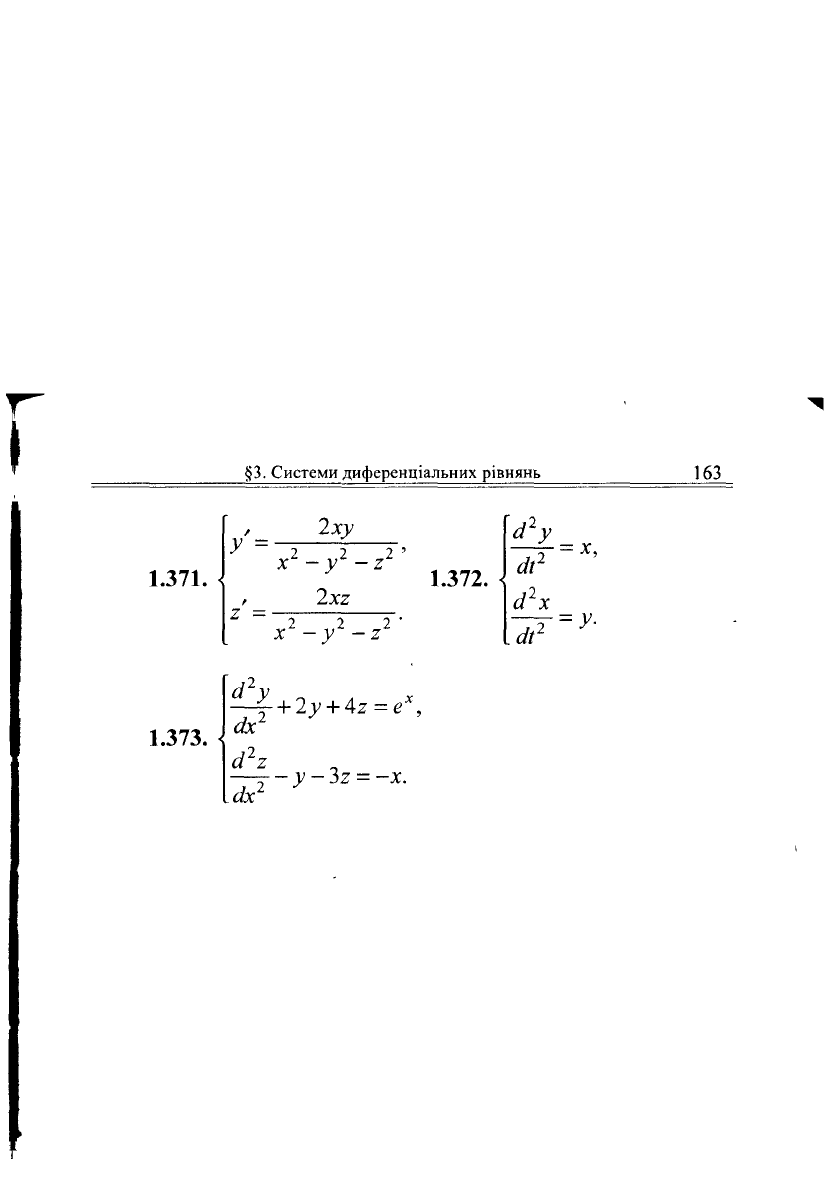
1.371.
У
2 =
2ху
2 2 2 '
X -у -2
2X2
X - у -2
1.372.
сії
2
^х
ІсІҐ
= х,
=
У-
&-
+
2у
+
Лг = е
х
,
ах

ГЛАВА
2.
РЯДИ
§1.
Числові ряди
І.
Короткі теоретичні відомості
Основні поняття. Нехай задано числову послідовність {и
п
}.
Вираз вигляду
щ + и
2
+...+ и„ +... = (2.1)
К=\
називається числовим рядом, числа и
к
- членами цьою ряду, и
п
-загаль-
ний член ряду.
Сума п перших членів ряду називається п -ю частинною сумою ряду
і позначається 5„ .
Отже,
п
5
„
=2>*
•
К=\
Якщо існує скінченна границя 5 послідовності \_8„ }, то кажуть, що
ряд збігається або ряд збіжний, і йоі о сума дорівнює 5 , тобто
Ііт
8„ = 8 .
У цьому випадку пишуть:
У випадку, коли Ііт 8
П
не існує, або дорівнює нескінченності, ряд
називається розбіжним.
Покладемо г
п
= 8-8
П
= и
п+]
+ и
п+2
+... .
Якщо Ііт 8
П
= 8 , то Ііт г
п
= 0 .
Величину г
п
називають п -м залишком ряду (2.1). Часто важливим є
питання оцінювання | г
п
| = 15 - 8
П
|. Оцінка | г
п
|
показує з якою точністю
частинна сума 8
П
наближує суму 5 ряду (2.1).
Необхідна умова збіжності ряду:
якщо ряд Х
м
« збігається, то
Ііт и„ = 0 . (2.2)
П—>ОО

§
1.
Числові ряди
165
Достатня умова розбіжності ряду:
якщо
Ііт
и„ * 0 , (2.3)
то ряд
2^і
и
п
розбігається.
/7=1
Критерій Коші збіжності ряду:
для гого,
щоб ряд ^ и
п
збігався, необхідно
та
достатньо,
щоб для
л=1
\/є > 0
існував такий номер
N , що для
всіх
п > N і
будь-якого натурально-
го числа
р,
виконувалась умова
к=п+\
<
Є.
Розглянемо найбільш важливі числові ряди.
На основі геометричної прогресії, тобто послідовності
\и
п
}, де
и
п
= аа",
створимо
ряд
а +
ад
+
аа
2
+...
+
а^г"
4
+...= • (
2
-4)
и=1
Цей
ряд для
стислості називатимемо також геометричною прогресі-
єю.
Використовують також назву геометричний
ряд.
Якщо
|о| < 1, ряд (2.4)
збігається,
то
його сума
5
обчислюється
за
формулою:
°°
л-1
5
=
Для
| д
\
>
1
ряд (2.4)
розбігається.
Гармонічний
ряд. Ряд
вигляду
І
+
І
+
і
+
...
+
І
+
...=
£! (2.5)
2
3 п
п=
\П
називається гармонічним.
Цей ряд
розбіжний.
Ряд вигляду
Х-'т, рєК (2.6)
л=1
Л
7
'
називається узагальненим гармонічним.
Він
збіжний
при /? > 1.

166
Глава 2. Ряди
Основні властивості збіжних рядів
1°.
Якщо ряд X
м
* збіжний і має суму 5 , то збіжним є ряд Х^
м
*
>
і=1 *=1
де С - константа і Х^"* ~ ^
•
і=1
2°.
Якщо ряди X
м
*
та
Х^' збіжні і мають суми 5, та 5
2
відповід-
к=\
к=і
но,
то збігається ряд Х(
м
*
+
у
к) і
має
суму 5, + 5
2
.
3°.
Сполучна властивість збіжного ряду. У збіжному ряді можна до-
вільно групувати члени, тобто якщо ряд X
м
*
є
збіжним, то збіжним є ряд
к=\
(«,
+и
2
+... + и
к]
)+ (и
к]+]
+ и
к |+2
+... + и
кі
) + (и
к
^
х
+ ... + и
Аз
) +
+
(И*3+!
+--- + "*
4
)+ ••• + («* „_,+1 +... + М
і()
) + ...,
утворений довільним об'єднанням його членів із збереженням порядку їх
прямування. Сума ряду при цьому не змінюється.
4°.
На збіжність ряду не впливає відкидання або приєднання скін-
ченної кількості членів ряду.
Наслідок. Ряд X
м
* збіжний (розбіжний) тоді і тільки тоді, коли збіж-
жі
ний (розбіжний) довільний його залишок.
Знакододатні ряди. Ознаки збіжності. Ряд вигляду
Х"и>
и
п
>0
/1=1
називається знакододатним рядом.
Теорема 1 {перша ознака порівняння). Нехай задано два ряди
І>«'"«
>0
(
2
-
7
)
и=1
1>
и
,У
л
>0
(2.8)
такі, що
и„<у„,Уп.

§ І. Числові ряди
167
Тоді, якщо
1) ряд (2.8) збіжний, то ряд (2.7) збіжний,
2) ряд (2.7) розбіжний, то ряд (2.8) розбіжний.
Ознака залишається в силі, якщо нерівність и
п
< у„ виконується не
для всіх п , а починаючи з деякого номера п-к.
Теорема 2 {гранична ознака порівняння). Нехай для рядів
]Ги„, и„ >0, 5>„, \
п
>0
/1 = 1 п=\
існує скінченна границя
Ііт
ІЬ.
=
і
Ф
о,
(це означає, що и
п
~ІУ„, п
—> °о
, зокрема, и„ ~ у„ , коли / = 1). Тоді обидва
ряди збіжні або обидва ряди розбіжні.
Теорема 3 (ознака Даламбера). Нехай для ряду
2Х-
"/>
>0
я=і
існує скінченна границя
Ііт
=ва-
=
І.
Тоді, якщо
1) / < 1, ряд збіжний,
2) / > 1, ряд розбіжний.
При / =
1
потрібне додагкове дослідження, бо ознака не дає відповіді
на питання ряд збіжний чи розбіжний.
Теорема 4 (радикальна ознака Коші). Нехай для ряду
існує скінченна границя
2>«>
и
п >°
/і=і
Ііт ФІ~ = 1.
Тоді, якщо
1) / < 1, ряд збіжний,
2) / > 1, ряд розбіжний.
При / = 1 потрібне додаткове дослідження.
Теорема 5 (інтегральна ознака Коші). Нехай для ряду

168
Глава 2. Ряди
виконується умова
щ> и
г
> щ>...
і існує незростаюча функція /(х) така, що
/(«) = и„, Уп.
Тоді невласний інтеграл \[/(х) сіх збіжний (розбіжний) одночасно з
і
заданим рядом X
м
,? •
,7=1
Зауваження. Можливо, що умови теореми виконуються, починаючи
з деякого номера п - к . У цьому випадку порівняння проводиться з невлас-
ним інтегралом ^ /(х) сіх.
к
Ряд
> —=
1
+ — + — + ... + — + ..., вєК,
£
х
п
р
2" З" п
р
що є узагальненим гармонічним (див. також (2.6)), збігається за теоремою 5
+
°° ах
при р > 1, бо збіжним є І при р > 1, а розбіжним при р< \ . Узагаль-
і х"
нений гармонічний ряд часто використовують при дослідженні збіжності
рядів за допомогою ознак порівняння (теорема 1, теорема 2).
Знакозмінні ряди. Числовий ряд, члени якого можуть бузи як додат-
ними, так і від'ємними, називають знакозмінннм.
Знакопочережним рядом називають ряд
щ-н
2
+и
і
-... +
(-\)"^и
п
+...=
%(-
л
Г^п,
и„>0, (2.9)
п=1
в якому знаки членів строго чергуються. Знакопочережний ряд є частинним
випадком знакозмінного ряду.
Теорема Лейбніца. Знакопочережний ряд (2.9) збігається, якщо
и
[
> и
2
> и
3
> ...
та
Ііт и
п
= 0 .
я—
Знакопочережний ряд (2.9), для якого виконуються умови теореми
Лейбніца, називають лейбніцевим рядом.

§
1.
Числові ряди
169
Найпростішими прикладами лейбніцевих рядів
є
ряди:
£НГІ
=1
_1
+
1
_.. +
(_,)-! І
+
(2.10)
и
=і
« 2 3 и
уН)!І
=
і_І
+
І_...
+(
_
1
)»->_!_
+
...
(2.іі)
^
2и-1 3 5 2и-1
Абсолютно
та
умовно збіжні ряди. Розглянемо довільний знакозмін-
ний
ряд
%„
•
(2-12)
Утворимо
ряд
з
абсолютних величин членів цього ряду
£|и
и
|.
(2.13)
/1=1
Ряд (2.13) знакододатний.
Теорема. Якщо
ряд
Х|
м
л|
збіжний,
то
збіжний
і
ряд
Х
м
и •
«=і
и=і
У випадку, коли
ряд Х|
и
л|
(2.13) збіжний,
ряд
(2.12)
^"л
назива-
ли
л=1
ють абсолютно збіжним. Кожний абсолютно збіжний
ряд
є
одночасно
і
збіж-
ним.
Проте
не
кожний збіжний знакозмінний
ряд
є
абсолютно збіжним.
Якщо
ряд
Х
м
л
збіжний,
а
ряд ХІ
м
л|
розбіжний,
то
ряд
Х
м
л
на
зи-
и=1
п=\ п=\
ваютьумовно збіжним. Умовно збіжними
є
ряди Лейбніца
У
(2.10)
«=і
»
Наслідок. Абсолютна похибка
від
заміни суми
5
ряду лейбніцевого
типу будь-якою частинною сумою
8
п
не
перевищує модуля першого
з
від-
кинутих членів ряду, тобто
\8-5„\йи
И+і
,
\г
п
\<и„
+х
.
Цим користуються
при
наближених обчисленнях.
Властивості абсолютно
та
умовно збіжних рядів
1°.
Якщо
ряд
Х
м
л
є
абсолютно збіжним,
то
абсолютно збіжним
є і
л=1
ряд
^Си
п
, де С =
СОП5І.
л=1

170
Глава 2. Ряди
2°.
Якщо ряди Х
м
«
та
Х
у
я абсолютно збіжні, то абсолютно збіж-
л=1 п-\
НИМИ
Є рЯДИ
Х("и
±У
л)-
л=1
3° (Сполучна властивість абсолютно збіжного ряду). У абсолютно
збіжному ряді можна довільно групувати члени, зберігаючи порядок їх пря-
мування, при цьому сума ряду не змінюється.
4°.
На абсолютну збіжність ряду не впливає відкидання або приєд-
нання скінченної кількості членів.
5°(Переставна властивість). Якщо ряд абсолюшо збіжний, то будь-
який ряд, уїворений за допомогою перестановки його членів, також абсо-
лютно збіжний і має ту саму суму, що і заданий ряд.
Теорема Рімана. Якщо ряд умовно збіжний, то яке б не було наперед
задане число р, можна так переставити члени цього ряду, що утворений
ряд матиме сумою саме те число р .
Числові ряди з комплексними членами. Нехай маємо послідовність
комплексних чисел {г
п
}, г„ = х
п
+ і у
п
. Комплексне число с = а + іЬ назива-
ють скінченною границею послідовності {г
п
}, якщо для довільного Є>0 іс-
нує номер N(г) такий, що для всіх п > N(г) мас місце нерівність: \г
п
—
с | < є.
Коротко це записується так:
Ііт г
п
= с.
Л—>«>
Якщо границя скінченна, послідовність називають збіжною, в іншо-
му разі - вона розбіжна.
Теорема. Для того, щоб послідовність {г
п
} мала скінченну границю
с = а + іЬ, необхідно і достатньо, щоб послідовності {х
п
} та {у
п
} мали
скінченні границі, які дорівнюють відповідно а і Ь .
Вираз вигляду
2,
+2
2
+... + 2
й
+...= !>„ (2.14)
л=1
називається числовим рядом з комплексними членами,
-
п
=
х
п +>У» - члениряду,
п
5„ - частинна сума ряду, 8„ = 2^-к •
Якщо існує скінченна границя
Ііт 8
п
= 8 ,
то ряд (2.14) збіжний, у противному випадку - розбіжний.
