Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§3.
Системи диференціальних рівнянь
151
або
або
З цією метою складаємо характеристичне рівняння
6-Х. 1
оеі(А-ХЕ) = =0.
5 2-Х,
Розкриваємо визначник
(6-Х)(2-Х)-5 = 0,
X
2
-8Х + 7 = 0.
Корені характеристичного рівняння X., = 7, Х
2
= 1 - дійсні, різні.
Система рівнянь для визначення власних векторів така:
(6-Х)х,+ х
2
=0,
5х
і
+(2-Х)х
2
=0.
При X, = 7 маємо
Х\
-Н
х
2
—
0,
і
л*|
—
Х-,,
ІX]
=
С,
5х,
- 5х
2
= 0
х
7
=С
х
2
=С.
Покладемо С = 1 . Тоді власний вектор V
При Х
2
=
1
маємо
5хі
~ь
Хл
!С]
"І"
Х
2
*2
=
0,
5Х]
+
х->
= 0
_
Х
2
х
2
= С
С
х, =-—,
х
2
= С.
Покладемо С = -5 . Тоді власний вектор V
а
2
) _
Отже, загальний розв'язок однорідної системи має вигляд
Х(0 = С,У
аі)
е
Х|
' +С
2
У
(Х2)
е
І2
' = С
]
є
11
+С
х,(0 = С,е
7
' +С
2
е',
х
2
(/) = С
1
в
7
' -5С
2
е'.
Загальний розв'язок неоднорідної системи шукаємо у вигляді:
е
7
' +С
2
(/)
ґ 1
-5
Х(/) = С,(/)
Складаємо систему для визначення С,'(/), С
2
(?):
с,'(0
е"+С
2
(()
-5

152
Глава 1, Диференціальні рівняння
Звідси
ІС'ДОе
7
' +С'
2
(і)е' = 1,
[с\(1)е
71
-5С
2
(і)е'
=1.
6С'
2
(1)е'
=(-\,
С'
2
(0-
1-І
Підставляючи це в перше рівняння системи, маємо
С\(1)е
7
'
+
^-е"е' = 1,
о
с (о =
5Г+1
Далі,
проінтегрувавши
С[(1),
С'
2
{і), отримаємо
с, (о = [ *±І
е
-т
л
= -{А,
+
А У
7
' + с,,
'
5
6 (42 49 ]
1
С,(/) = [— є'
1
сії = - -іе
4
+С
2
.
6 6
Отже,
загальний розв'язок заданої неоднорідної системи такий:
хм-' "
2
= С
Г
1
і
е
ь
+С,
42 49
-5
+ С, в
11
;
5 2
Є
-/
42 49 6
5 2
5
і. /
42 49
т і
6 ;
або
2 2 А
С,е
7
' +
С
2
е'--(
2
7 49
5 _2
1 49]
п Ті С/~І І , -
1
<
2
С(Є
-5С
2
е
+ — І
х,(0 = С,е
7
'
+С
2
е'--(-—,
1 2
7 49
х
2
(/) = С,е
7/
-5С,е' +-/-—.
2
" 7 49
Спосіб 3. Метод підбору вигляду частинного розв'язку за виглядом
правої частини (метод невизначених коефіцієнтів).
Для заданої неоднорідної системи
сіх.
сії
сіх
2
сії
- - 6х, + х
2
+ /,
= 5х, +2х
2
+1

§3.
Системи диференціальних рівнянь
153
(6 1\ (І
матриця А =
І
^ І, функція ¥(1) =
Відповідна однорідна система
сіх
сії
-
= 6х, + х
2
,
сіх
2__
л
=
5лГ) + 2х
2
.
Знаходимо її загальний розв'язок.
Характеристичне рівняння
6-Х 1
йеі(А-ХЕ) =
= 0.
5 2-Х
Корені характеристичного рівняння Х
і
= 7, Х
2
= 1 - дійсні, різні.
Власні вектори знаходяться з системи:
\(6-Х)х
]
+ х
2
= 0,
[ 5х^+(2-Х)х
2
=0
при X = Х,| =7 та при Х = Х
2
=\ і є такими:
/•(Лі)
л(Л
2
)
-5
(див.
спосіб 2).
Загальний розв'язок однорідної системи:
х(0
=
с
Частинний розв'язок неоднорідної системи шукаємо у вигляді:
'АІ+В^
Сі+Б
бо Р(0
=
(ґ
)
Л
Х(0 =
тобто /І(0 = / -МНОГОЧЛЕНСТЕПЕНЯ X] = 1, /
2
(і) = 1
многочлен степеня з
2
= 0,
тах(5
]
,5
2
)
= 5 = 1, що й зумовлює вигляд Х(і);
функції
/\(1),
/
2
(і) не містять е
ш
, тобто а = 0 і не співпадає з коренями
характеристичного многочлена.
Отже,
ї,
(/) = Аі + В, х[{1) = А,
х
г
(і)
= Сі+й, х'
2
(і) = С.
154
Глава 1. Диференціальні рівняння
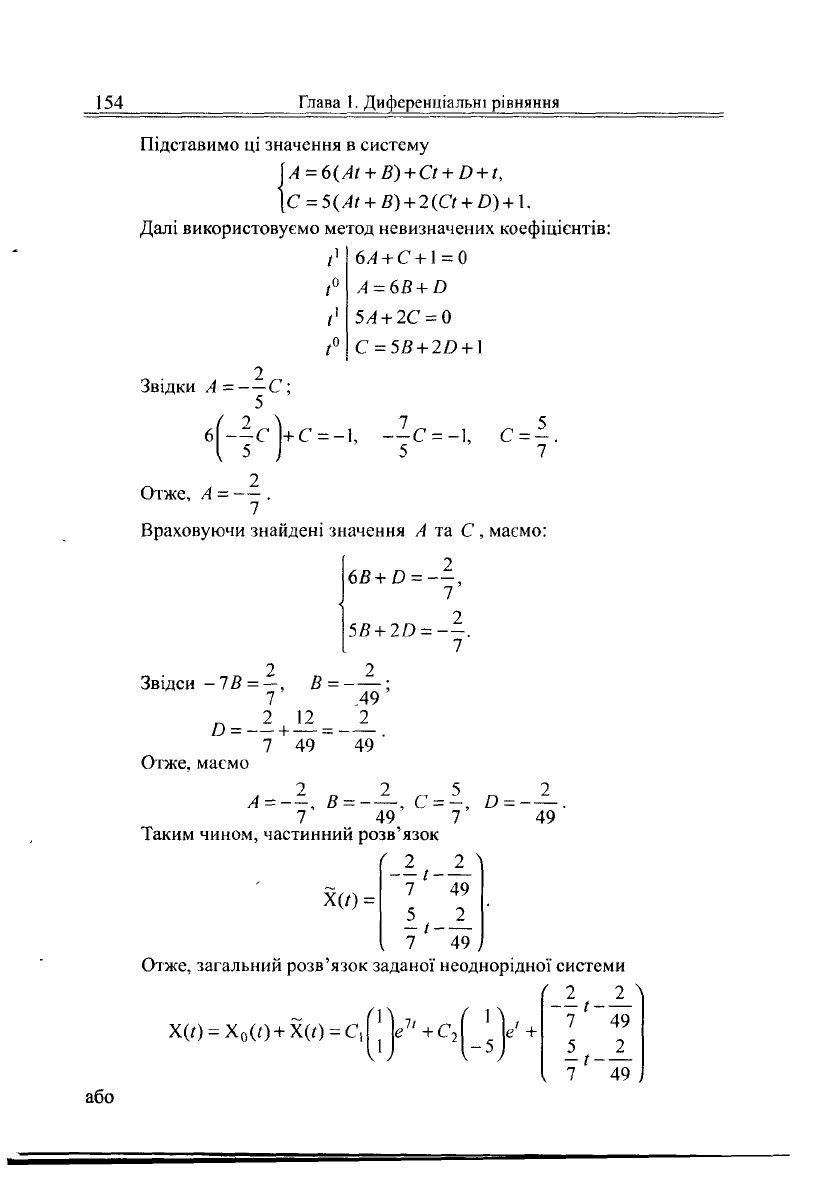
Підставимо ці значення в систему
\А = 6(Аі + В) + Сі + 0 + 1,
|С = 5(Лг+Я) + 2(0 + £>) + 1.
Далі використовуємо метод невизначених коефіцієнтів:
6Л + С +
1
=0
А=6В + 0
5А + 2С = 0
С = 5В + Ю + \
Звідки А = С;
5
( 2 \ 1
6 С +С =
-1,
—С =
-
5 5
С=-
Отже, /1 = -
:
Враховуючи знайдені значення А та С , маємо:
6В+0 = ,
7
5Д + 20 = --
Звідси -75 = -, б = ;
7 .49
2 12 2
0 = -- + — = -— .
7 49 49
Отже, маємо
2 2 5 2
/4=--,
В = -~, С=-, 0 = - —
7 49 7 49
Таким чином, частинний розв'язок
Х(/) =
Отже, загальний розв'язок заданої неоднорідної системи
' 2
2 ї
7
^
49
5 2
/
49
, 7
2
/
49
х(г) =
х
0
(о+х(0
=
с,
7
, ( \\
е
1
' +С
-5
е +
2 2 А
7 ~49
5 2
— 1-
7 49
або

§3.
Системи диференціальних рівнянь
155
х,(0 = С,е
7
' +
С,е'--(-—,
11
" 7 49
х
2
{і)
= С,е
7
'-5С
2
е' + -/-—.
21 2
7 49
Порівняння показує, що всі три способи розв'язання привели до од-
ного й того ж результату.
Приклад 17. Розв'язати задачу Коші
%
=
4у,
~5у
2
+ 4х + 1,
сії
сіу
2
сії
=
У\
-
2
Уі +
х
при _у,(0) = 1, у
2
(0) = 2.
• Маємо лінійну неоднорідну систему зі сталими коефіцієнтами. Для
розв'язання скористаємось методом варіації довільних сталих.
Перш за все знайдемо загальний розв'язок відповідної однорідної
системи
\у'\
=
4
У\ ~
5
У2>
[У2 =Уі ~
2х
2-
Корені її характеристичного рівняння Х\ =—1, Х
2
= 3.
Власні вектори V
рідної системи:
у(*.2>
=
VI/
, а загальний розв язок одно-
У(0 = С,
або
у
і
(х)
=
С
і
е~
х
+ 5С
2
е
3
\
у
2
(х)
=
С
х
е-
х
+
С
2
е
3х
(перевірте!).
Загальний розв'язок неоднорідної системи шукаємо у вигляді:
у
]
(х)
= С
]
(х)е-
х
+5С
2
(х)е'
х
,
у
2
(х) = С, (х) е"
х
+С
2
(х) е
іх
.
Далі знаходимо
у[ =С{(х)е'
х
-С
х
{х)е~
х
+5С'
2
(х)е
3х
+15С
2
(х)е
3х
,
у
2
= С,'(х) е'
х
- С, (х) е"
х
+ С
2
(х) е
3х
+ ЗС
2
(х) е
3х
.

156
Глава 1. Диференціальні рівняння
Отримані функції
у
х
, у
2
, у\, у'
2
підставимо
в
задану систему. Після зве-
дення подібних членів, отримуємо систему відносно невідомих С\(х),
С'
2
(х):
\С\(х)
е~
х
+ 5С'
2
(х) е
іх
= Ах +1,
\с[(х)е'
х
+
С'
2
(х)е
3х
=х.
Розв'язавши систему, отримуємо
с\{Х)=и
х
-\)е
х
,
4
С'Ах)=\(Зх-\)е-'
х
.
4
Зауважимо,
що в
попередньому прикладі вказана система була запи-
сана формально
без
попереднього підставляння функцій
та їх
похідних
у
систему.
Далі, проінтегрувавши відповідні рівності, знаходимо
С, (х), С
2
(х) ;
С,(х)
= і
(х-2)е
х
+ С,, С
2
(х) = ~ (Зх
+ 2)є'
3г
+
С
2
.
Отже, загальний розв'язок заданої неоднорідної системи
у
]
(х) =
С,
е'
х
+
5С
2
е
іх
+
^ (х - 2) - (Зх
+
2) ,
у
2
(х) =
С,
е~
х
+
С
2
е'
х
+
і (х -
2)
- -1 (Зх
+
2) .
Враховуючи початкові умови уДО)
= 1,
у-,(0)
= 2 ,
складаємо систе-
му
для
визначення
С,, С
2
:
=
С,
+5С
2
2
= С, + С
2
2
6
1_і
2
6'
Звідси
С, = —, =——.
'
4
2
12
Отже, частинний розв'язок вихідної системи,
що
задовольняє вказані
початкові умови,
має
вигляд:
У
(х)
= — е'
х
- — е
іх
+-0-2)-—
(Зх
+
2) ,
'4
12 4 12
у,(х)
= —
е~
х
-~е
іх
+-(х-2)-—
(Зх
+
2) . М
-
4 12 4 12

§3.
Системи диференціальних рівнянь
157
Приклад
18.
Знайти частинний розв'язок системи
сіх
х
сії
сіх
2
. сії
- х
х
+е
• Для цієї лінійної неоднорідної системи диференціальних рівнянь зі
сталими коефіцієнтами маємо:
а) для першого рівняння системи функцією /, (і) є многочлен друго-
го степеня: /] (?) = І
2
;
б) для другого рівняння системи /
2
(і)
—
е'.
Характеристичне рівняння
-X -1
аег(А-АЕ) =
1 -X
0
має корені Х
Х2
= ±/.
Частинний розв'язок заданої системи відшукуємо у вигляді, аналогіч-
ному функціям /ДО і /
2
(0' тобто у вигляді суми многочлена другого сте-
пеня А,і
2
+ В,1 + С, і функції вигляду е', де А
І
, В,, С,, £>,, / = 1,2 - ста-
лі,
бо число а =
1
не є коренем характеристичного рівняння. Отже,
х
х
= А
х
1
2
+ В
х
і + С
х
+ й
х
е',
х
г
= А
2
1
2
+ В
2
1 + С
2
+0
2
е'.
Підставивши ці функції в задану систему, отримуємо
І2А
Х
1+В
Х
+ О
х
е'
=~А
2
1
2
-
В
2
1-С
2
-
й
2
е' -VI
2
,
[2А
2
(+В
2
+£>
2
е' = А
х
1
2
+ В
х
1 + С
х
+0,е' +е'.
Прирівнявши коефіцієнти при однакових степенях / та при е' в обох
рівняннях, отримуємо:
І
2
1-А
2
=0
/
2
Л,
=0
I
Х
2А
Х
=-В
2
г
1
2Л
2
= В,
1°
Вх =-С
2
/°
В
2
=С
Х
е'
А =-£>
2
е'
£
2
= Д +1
Звідки
^,=^=^=0,
А
2
=\, В, - 2,
С
2
=-2,
£>]=--,
^2=2

158
Глава
1.
Диференціальні рівняння
Шуканий частинний розв'язок
має
вигляд:
х,
=21-
х
2
=І
2
-2 + —.
2
2
IV. Задачі для практичних занять
Основні поняття
1.331. Перевірити,
що
функції
у{х) та г(х) є
розв'язками
вказаних диференціальних рівнянь:
а)
б)
ду
дх
дг_
=
]_
дх
у
Ф
=1_
дх
дг
дх
2
у(х) = е
2
, г(х) = 2е
2
;
У(Х)=-
+ —
,
2(Х) = Є
Х
-- + ~
Т
2у
3 х
1
3 х
у + г +
1,
X
У задачах 1.332
- 1.335 для
заданих систем знайти фазові
траєкторії,
що
проходять через задані точки
М
0
.
1.332.
дх
2 2
--1-х
ді
М
0
(1,2).
дх
1.333.
дх
2 2
1.334.
ді
= 2х,
—
= х +
2у,
їді
М
0
(1,1).
1.335.
М
0
(2,1).
г
дх
—
= у
-
х,
ді
ду
~дї
М
0
(1,1).
=
у-2х,

§3.
Системи диференціальних рівнянь
159
Лінійні системи диференціальних рівнянь
із змінними коефіцієнтами
У задачах 1.336 - 1.339 розв'язати задані лінійні системи
диференціальних рівнянь.
1.336.
\
1.338.
сіх
СІ2
СІХ
СІХ
сії
сіу
сії
У
+ Х2,
X
її
х
3
У_
І
X
І'
1.337.
1.339.
сіу
X = -у + Х2,
СІХ
2СІ2
х — = -2у + ху.
ах
сіх _ 2
сії І
сіу
1
+ 2
-^- = у + х.
сії І
Лінійні однорідні системи диференціальних
рівнянь зі сталими коефіцієнтами
У задачах 1.340 - 1.354 розв'язати задані лінійні однорід-
ні системи диференціальних рівнянь зі сталими коефіцієнтами,
використовуючи: а) метод виключення, б) метод Ейлера. Там,
де задані початкові умови, крім загального розв'язку, знайти від-
повідний частинний розв'язок.
1.340.
сіх
—
=
їх + у,
сії
сіу
сії
1.341.
= Зх + Ау.
1.342.
1.344.
сіх „
а
=х+3у
-
сіу .
— = -х + 5у,
сії
х(0) = 3, 7(0) = 1
сіх
л
=у
-
7х
>
^ = -2х-5у.
сії
1.343.
1.345.
сіх
сії
сії
сіх
сії
ф
У сії
сіх
сії
сіу
[сії
=
У>
- -2х + Зу.
= х-3у,
= 3х +.у.
= 2х- 5у,
5х - 6у.
160
Глава І. Диференціальні рівняння
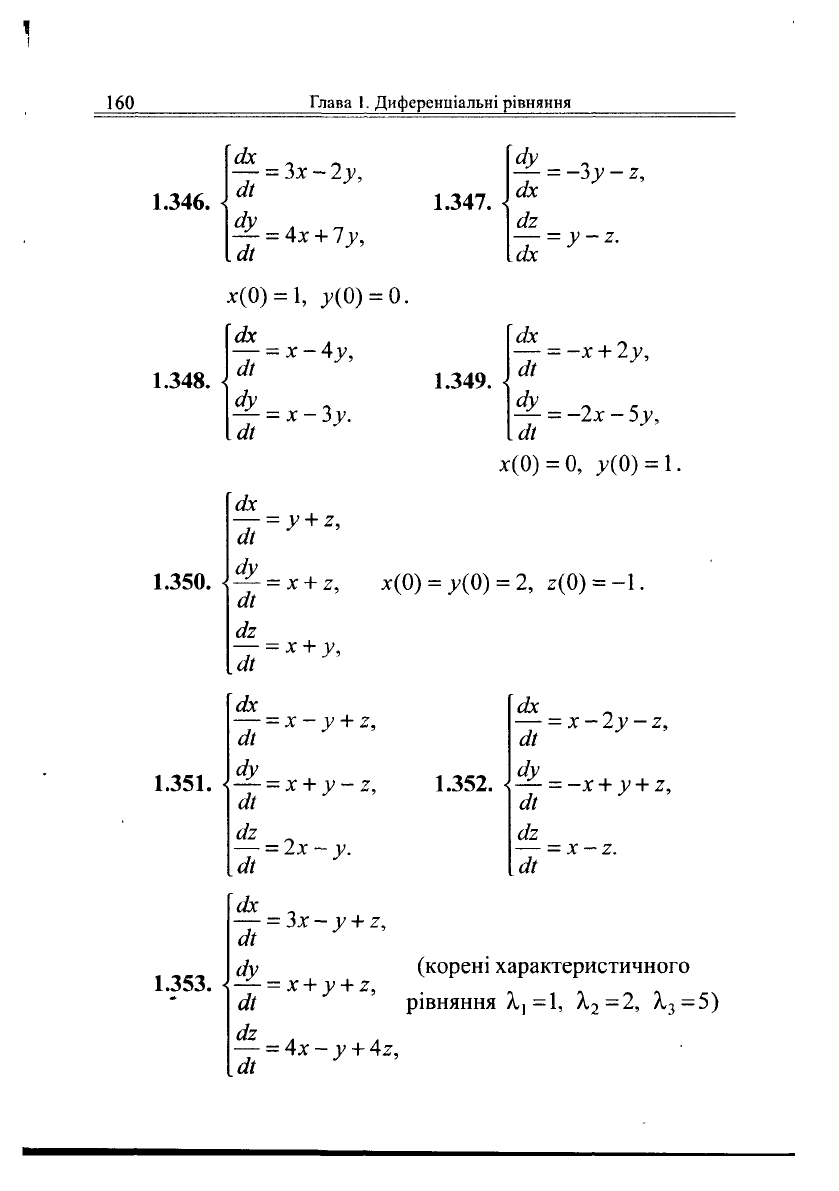
1.346.
сіх
сії
±
[сії
Зх~2у,
•
4х + 7
у,
1.347.
-^- = -Зу-г,
сіх
СІ2
сіх
х(0) = 1, у(0) = 0.
сіх
1.348.
1.350.
1.351.
1.353.
сії
ІІІ
сіх
Ні
сіу
ЇЇ
СІ2
її
сіх
сії
±
сії
СІ2
їй
ск
сії
сії
СІ2
~СЇІ
х - 4у,
х-Зу.
1.349.
сіх
сії
ф
[сії
х(0) = 0, у(0) = \,
-х + 2у,
•
= -2х - 5у,
•У+ 2,
•х + 2, х(0) = у(0) = 2, г(0) = -1
х + у,
= X - у + 2,
= X + у - 2,
= 2х ~ у.
= Зх-у + 2,
= Х + у + 2,
= 4х-у + 4г,
1.352.
сіх
Л
= X - 2
V
- 2,
сії
сіу
сії
СІ2
сії
= -Х + у + 2,
•
= X - 2.
(корені характеристичного
рівняння Х| =
1,
Х
2
=2,
Х-з
= 5)
