Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3

Подождите немного. Документ загружается.

§3.

Системи диференціальних рівнянь

121

Для нормальної системи (1.115) справджується теорема Коші про іс-

нування та сдиністьрозв 'язку: якщо в деякій області О функції /,,

/•>,...,

/„ ,

що є правими частинами системи (1.115), неперервні разом з частинними гю-

~\Ґ

хідними ——, /,_/ = 1, п , то для будь-якої точки М

(х

, у{\

,...,у^)в

існує єдиний розв'язок у,(х),

(х),...,

у„(х), який задовольняє початкові

умови (1.116)

У\(х

)

= У°,

{х

)

,...,

(х

)

= у°

Загальним розв 'язком системи (1.115) називається сукупність функцій

у,

у,(х,С

]

,...,С

/ = ЇЯ 0-П7)

що залежать від п довільних сталих, які при будь-яких припустимих зна-

ченнях С|,..., С„ перетворюють рівняння системи (1.115) в тотожності і для

будь-яких початкових умов (1.116) існують такі числа С, = С,° , що функції

у,

= у, (х, С'|°,..., С°), / = 1, п , задовольняють ці умови.

Розв'язки, які отримуються з загального розв'язку при конкретних

значеннях С С

, називаються частинними розв'язками.

Диференціальне рівняння п -го порядку

л)

=/(х^,/,...,У

) (1.118)

можна звести до нормальної системи (1.115). І навпаки, система (1.115) в

багатьох випадках зводиться до одного диференціального рівняння п -го

порядку.

На цьому основано метод виключення для розв'язання нормальної

системи диференціальних рівнянь (1.115), згідно з яким ця система зводить-

ся до одного диференціального рівняння п -го порядку вигляду (1.118), яке

розв'язується розглянутими раніше в § 2 цієї глави методами.

Фізичний зміст нормальної системи. Нехай незалежна змінна І

—

це

час,

а система, наприклад, двох диференціальних рівнянь має вигляд

Лх

— = /,(/, х, у),

(1.119)

^ = /

С х,у).

аі

Розв'язком х = ф(/), у = \)/(/) цієї системи є деяка крива (інтегральна

крива) в площині хОу з фіксованою декартовою прямокутною системою

координат. Площина хОу називається фазовою площиною, а крива

х = ф(/), у = - фазовою траєкторією системи (1.119). Сама система

(1.119) називається динамічною системою. Якщо в праві частини рівнянь

системи (1.119) час І не входить явним чином, то така динамічна система

називається автономною (стаціонарною).

122

Глава 1, Диференціальні рівняння

Динамічна система визначає поле швидкостей точки,

що

рухається,

будь-який момент часу

Розв'язок

х = х((), у = >'(/)

динамічної системи

це рівняння руху точки,

які

визначають положення точки,

що

рухається,

будь-який момент часу

І.

Початкові умови задають положення точки

початковий момент:

х(<о)

о>

УІЇо)

= По-

РІВНЯННЯ руху визначають також

траєкторію руху, будучи рівняння-

ми цієї кривої

параметричній формі.

Лінійні системи диференціальних рівнянь. Загальна теорія

Система диференціальних рівнянь називається лінійною, якщо вона

лінійна відносно всіх невідомих функцій

та їх

похідних.

Лінійні однорідні системи диференціальних рівнянь

Нормальна лінійна однорідна система

п -го

порядку

має

вигляд

сіх.

сії

сіх

~сТі

сії

•

я,

,(/)*,

+а

(')х

+ ...+

Хп

(і)х

•

(г)*і

(і)х

+...+ а

2і

,(1)х

)П

й„і(/)Х|

+а

п2

{і)х

+ ... + а

п)І

{і)х„

або

матричній формі

де

(1.120)

сіХ

йі

А(і)Х(1),

(

'о

о,

(/)..

•

а,„(0'

'*,(')'

'*[(')

А(0

{і) а

(і)..

•

2я

Х(0

(і)

сіХ

сії ~

(,)

п]

(і) а„

(і)..

• а„,М),

(1.121)

В області неперервносі

коефіцієнтів

о,

;

(/),

/, / = 1, п,

система (1.120)

задовольняє умови теореми існування

єдиності розв'язку задачі Коші.

Фундаментальною системою розв 'язків системи (1.120) називається

сукупність

лінійно незалежних розв'язків цієї системи

{і)

(х\

\і),х

(к

\і) х]

\і))>,

к=~п.

(1.122)

§3.

Системи диференціальних рівнянь

123

Структура загального розв 'язку однорідної системи диференціаль-

них рівнянь. Загальний розв'язок однорідної системи диференціальних рів-

нянь (1.120) представлясіься у вигляді

Х(/) =

£С,Х,(0,

(1.123)

де

(і),

к = \,п - фундаментальна система розв'язків цієї системи,

Сі,С

,...,С„ - довільні с галі.

Лінійні неоднорідні системи диференціальних рівнянь

Нормальна лінійна неоднорідна система п -го порядку має вигляд

ах.

—-^- = а,

,(/)*, +а

(і)х

+...

+ а

,(і)х„

+ Мі),

аі

ах

~аТ

(і)х

]

+а

(1)х

+... +

2п

(1)х„

(1),

(1.124)

сіх

—г-

(і)х

п2

(1)х

+...+

пп

(і)х

+/„((),

сії

де хоча б одна з функцій /

(І) тотожно не дорівнює нулю.

У матричній формі ця система має вигляд

сіХ

сії

А(/)Х(0+Р(0,

де

Р(0

(/і(0./

(0)

(1.125)

(1.126)

Відповідна однорідна система рівнянь для системи (1.124) має вигляд

сіХ

сії

•

= А(/)Х(/).

;і.і27)

Структура загального розв 'язку неоднорідної системи диференціаль-

них рівнянь. Загальний розв'язок неоднорідної системи диференціальних

рівнянь (1.124) представляється у вигляді

х(/)

(/)

х(0,

(1.128)

де Х

(/) - загальний розв'язок відповідної однорідної системи, Х(і) - де-

який частинний розв'язок заданої неоднорідної системи (1.124).

Методи розв'язання лінійних однорідних систем диференціальних

рівнянь

Метод виключення, оснований на зведенні системи до одного од-

норідного диференціального рівняння п -го порядку.

124

Глава 1. Диференціальні рівняння

Метод Ейлера, призначений для систем диференціальних рівнянь

зі сталими коефіцієнтами (наводиться нижче).

Методи розв'язання лінійних неоднорідних систем диференціа-

льних рівнянь

Метод виключення, оснований на зведенні системи до одного не-

однорідного диференціального рівняння п -го порядку.

Метод варіації довільних сталих (метод Лагранжа).

Метод підбору вигляду частинного розв'язку за спеціальним вигля-

дом правої частини, призначений для систем диференціальних рівнянь зі

сталими коефіцієнтами (наводиться нижче). При цьому загальний розв'язок

знаходиться за формулою (1.128).

Розглянемо детально метод варіації довільних сталих.

Нехай задана лінійна неоднорідна система диференціальних рівнянь

~ = А(()Х(0+Р(0.

сії

Відповідна їй однорідна система

^• = А(/)Х(0.

Нехай відома фундаментальна система розв'язків однорідної систе-

ми:

(1),

к = \,п. Загальний розв'язок однорідної системи представля-

ється у вигляді

Х(0 = ІС,Х

(/),

к=\

де С

, к = 1, п - довільні сталі.

Загальний розв'язок неоднорідної системи шукаємо у вигляді

Х(0=Х

*(')Х*(/),

(1.129)

к=\

де функції С

(І), к = \, п , визначаються з умови того, щоб Х(() було роз-

в'язком системи (1.125).

Підставляємо (1.129) в неоднорідну систему (1.125) і, враховуючи при

цьому рівності

сіХ

-А(/)Х*(/) = 0, к = \,п,

аі

с!С

(і)

приходимо до системи алгебраїчних рівнянь відносно

§3.

Системи диференціальних рівнянь

125

£^>Х

(О=Р(О.

сії

(1.130)

З цієї системи знаходимо

сіС

(1)

сії

•

(і) та, інтегруючи, отримуємо

функції С

((), к = \,п,з точністю до довільних сталих. Підставляючи їх у

(1.129),

маємо шуканий загальний розв'язок неоднорідної системи (1.125).

Лінійні однорідні системи диференціальних рівнянь зі сталими

коефіцієнтами

Лінійна однорідна система диференціальних рівнянь зі сталими кое-

фіцієнтами має вигляд

АХ(,),

сії

(1.131)

де

А =

'а

... а

1п

22 —а

2п

Х(/) =

(1)

сіХ _

х'

(і)

п1

п2

... а

Тут А - матриця коефіцієнтів а

системи, де а

—

сталі, /,_/'= 1, п .

Розглянемо метод Ейлера для розв'язання такої системи. У цьому

методі для відшукання фундаментальної системи розв'язків використову-

ються методи лінійної алгебри.

Суть методу Ейлера така.

Складаємо характеристичне рівняння

аеІ(А-А.Е) = 0. (1.132)

Далі знаходимо його корені

,Х

,...,Х

- власні значення матриці

А і для кожного кореня Х

, к = 1, п (з урахуванням його кратності), визна-

чається відповідний йому частинний розв'язок

Х^

\і)

Загальний розв'язок системи (1.131) мас вигляд

х(0 =

Іс

(А

*>(/),

(1.133)

де

Х^

\і)

- лінійно незалежні розв'язки системи.

При цьому можливі такі випадки:

а) X - дійсний корінь кратності 1. Тоді

126

Глава 1. Диференціальні рівняння

{

Х)

а)

(1.134)

де V

(X)

власний вектор матриці А, який відповідає власному значенню

X, тобто

АУ

(Х)

=ЛУ

б) X - комплексний корінь кратності І. Тоді коренем характеристично-

го рівняння

(1.132)/Є

також спряжене з А. число X . Замість комплексних час-

тинних розв'язків Х

(і)

(ї) та Х

(

^(') треба взяти дійсні частинні розв'язки

<Х)

(і)

КеХ

(Х)

(1),

{Х)

(і)=\тХ

{Х

\і);

(1.135)

в) X - корінь кратності г > 2 . Відповідний цьому кореню розв'язок

системи (1.131) відшукується у вигляді вектора

{Х)

(і)

„(2),

аУ

)

+а

...

''У-'

(1.136)

Коефіцієнти /, у = 1, п , визначаються із системи лінійних рів-

нянь,

яка отримується прирівнянням коефіцієнтів при однакових степенях

і внаслідок підстановки вектора (1.136) в початкову систему (1.131) (метод

невизначених коефіцієнтів).

Лінійні неоднорідні системи диференціальних рівнянь зі сталими

коефіцієнтами

Лінійна неоднорідна система диференціальних рівнянь зі сталими

коефіцієнтами має вигляд

^•

= АХ(/) + Р(0,

(1.137)

де

А - матриця коефіцієнтів а,

системи, де а,

- сталі, і,]-\,п,

Р(0

(/і(0,

М*),~;

/ДО)' , /ДО,

і =

1п - задані функції.

§3.

Системи диференціальних рівнянь

127

Загальний розв'язок такої системи представляється

вигляді

Х(/)

= Х

(/) +

Х(/),

(1.138)

де

(0 -

загальний розв'язок відповідної однорідної системи

(1.139)

Х(/)

деякий частинний розв'язок неоднорідної системи (1.137).

Для відшукання загального розв'язку відповідної однорідної системи

використовуються відомі методи: метод виключення

або

мегод Ейлера.

Для відшукання частинного розв'язку неоднорідної системи може буги

використаний метод підбору вигляду частинного розв'язку

за

спеціальним

виглядом правої частини (метод невизначених коефіцієнтів).

Цей метод застосовується, коли функції

(

(/),

/ = 1, п, які

стоять

пра-

вій частині системи, мають спеціальний вигляд: многочлени

(і) ,

показни-

кові функції

синуси

косинуси

зіп

(З/

со$|3/ та

добутки

цих

функцій.

Тобто, якщо функції

/, (І), і = 1, п ,

мають вигляд добутків

де

Р(1), (2(1)

-многочлени,

то

частинний розв'язок

Х(/)

можна знайти

ме-

тодом невизначених коефіцієнтів, записавши

Х(/) у

вигляді, аналогічному

(1.140)

урахуванням співпадіння

або не

співпадіння чисел

а± ф з

кореня-

ми характеристичного рівняння.

Маємо підхід аналогічний тому,

що мас

місце

при

розгляданні неод-

норідних диференціальних рівнянь /7-го порядку

зі

сталими коефіцієнта-

ми.

При

цьому можливе застосування принципу суперпозиції.

У більш складних випадках, коли

не

вдасться звести праву частину

до

вказаного спеціального вигляду, використовується метод варіації довільних

сталих.

//. Контрольні питання

та

завдання

Яка

система диференціальних рівнянь називається

ка-

нонічною?

Яка

система диференціальних рівнянь називається нор-

мальною?

Як

ставиться задача Коші

для

нормальної системи

ди-

ференціальних рівнянь?

Що

називається загальним розв'язком нормальної сис-

теми диференціальних рівнянь?

(0соз(3/ +

(2(08ІпР/)е

(

(1.140)

128

Глава 1. Диференціальні рівняння

Наведіть фізичний зміст нормальної системи диферен-

ціальних рівнянь.

6. Запишіть лінійну однорідну систему диференціальних

рівнянь.

Дайте означення фундаментальної системи розв'язків

однорідної системи диференціальних рівнянь.

8. Яка структура загального розв'язку лінійної однорідної

системи диференціальних рівнянь?

9. Запишіть лінійну неоднорідну систему диференціаль-

них рівнянь.

10.

Яка структура загального розв'язку лінійної неоднорід-

ної системи диференціальних рівнянь?

11.

Наведіть методи інтегрування лінійної однорідної сис-

теми диференціальних рівнянь.

12.

Наведіть методи інтеїрування лінійної неоднорідної сис-

теми диференціальних рівнянь.

13.

У чому полягає метод виключення для однорідних сис-

тем; для неоднорідних систем?

14.

У чому полягає метод варіації довільних сталих (метод

Лагранжа) для неоднорідної системи?

15.

Запишіть у матричному вигляді однорідну систему ди-

ференціальних рівнянь зі сталими коефіцієнтами.

16.

Яке рівняння називається характеристичним? Запишіть

його.

17.

Викладіть суть методу Ейлера розв'язання лінійних одно-

рідних систем диференціальних рівнянь зі сталими коефіцієнтами.

18.

Який частинний розв'язок системи відповідає простому

кореню характеристичного рівняння; кратному кореню кратнос-

ті г > 2 ; комплексно-спряженому кореню?

19.

Запишіть у матричному вигляді неоднорідну систему ди-

ференціальних рівнянь зі сталими коефіцієнтами.

20.

У чому полягає метод підбору вигляду частинного роз-

в'язку лінійної неоднорідної системи диференціальних рівнянь

§3.

Системи диференціальних рівнянь

129

за спеціальним виглядом правої частини? Які спеціальні вигля-

ди правої частини при цьому використовуються?

///.

Приклади розв'язання задач

У цьому пункті розглянуто

прикладів розв'язання

за-

дач,

які за

своєю тематикою розподілились

так:

Основні поняття: приклади

1-8.

Лінійні системи диференціальних рівнянь

із

змінними

коефіцієнтами: приклади

9-11.

Лінійні однорідні системи диференціальних рівнянь

зі

сталими коефіцієнтами: приклади

12 - 15.

Лінійні неоднорідні системи диференціальних рівнянь

зі сталими коефіцієнтами: приклади 16

- 18.

Основні поняття

Приклад

Звести канонічну систему диференціальних

рівнянь

\У\=ІУ\

-ІУ2>

Хуі

=У\~ 2у

до нормального вигляду.

• Покладемо

у\ = у

, у'

= у

Тоді задану систему можна записати

вигляді

'У\=Уп

•

Уг

=У4>

Уг

Уі -Ьг,

У\ =У\

-2Уг>

яка

і є

нормальною системою четвертого порядку.

Приклад 2. Звести

до

нормальної системи задане диферен-

ціальне рівняння

у\х)

+ к

у(х) =

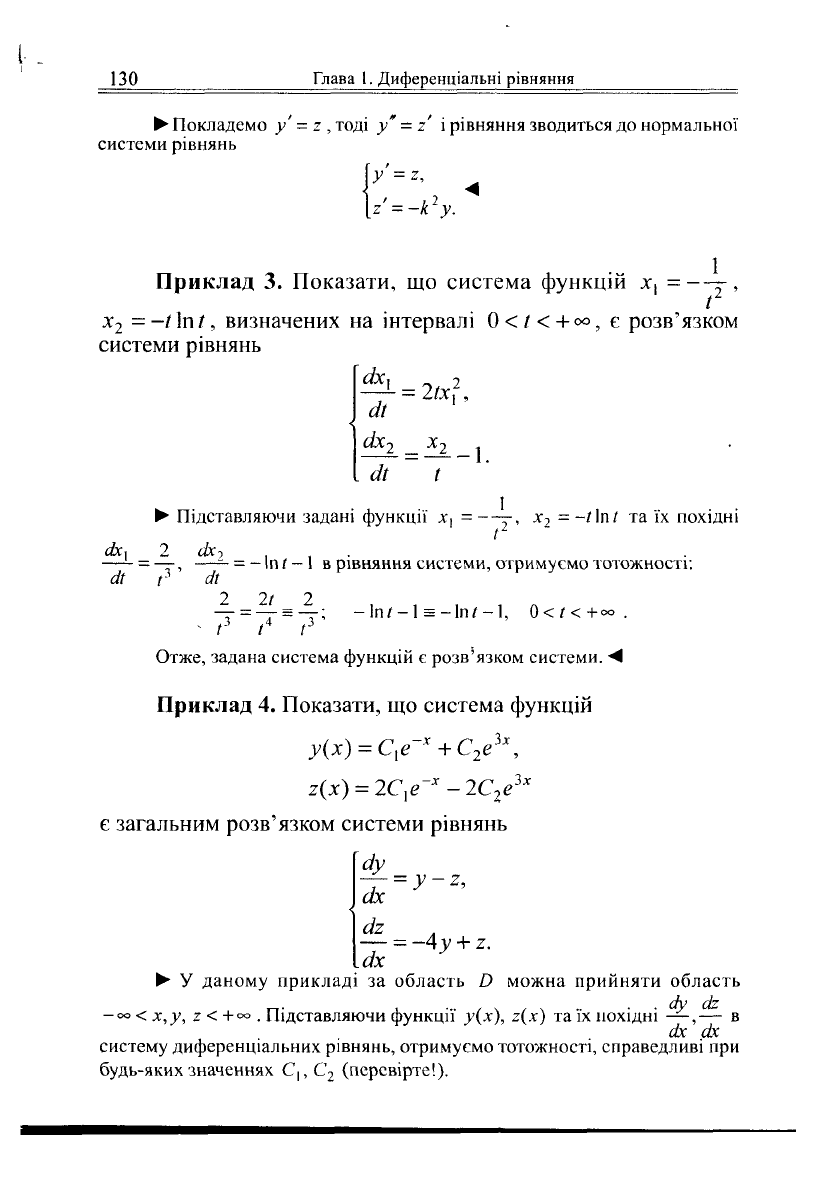
130

Глава 1. Диференціальні рівняння

• Покладемо у' = г , тоді у" = 2 і рівняння зводиться до нормальної

системи рівнянь

2=-к

у.

Приклад 3. Показати, що система функцій х, =-\,

=-/1п/, визначених на інтервалі 0</<+°°, є розв'язком

системи рівнянь

^- = 2/х

сії

сії І

• Підставляючи задані функції х, =

сіх

сії

-11п / та їх похідні

—, —— = -1п*-1 в рівняння системи, отримуємо тотожності:

сії

2 21 2 , .

— = — = —; -1п/-1 =

-1п/-1,

0</<+оо.

- I

Отже, задана система функцій є розв'язком системи. А

Приклад 4. Показати, що система функцій

їх

у(х)

= С

е~

+С

е'

г(х) = 2С,е~

- 2С

є загальним розв'язком системи рівнянь

Сіу

їх

СІХ

СІ2

СІХ

= У~2,

= -Ау +1.

• У даному прикладі за область О можна прийняти область

—

°°

х,у,

2 < +°° . Підставляючи функції

у(х),

г(х)

та їх похідні — в

сіх сіх

систему диференціальних рівнянь, отримуємо тотожності, справедливі при

будь-яких значеннях

(перевірте!).